外界載荷對圓柱渦激振動能量轉換的影響

王軍雷，冉景煜，張智恩，張 力，蒲 舸，丁 林

（重慶大學 低品位能源利用技術及系統教育部重點實驗室，重慶400044）

近年來，收集流體中微弱流動能是國內外廣泛關注的熱點.微小型風力收集裝置能夠在無人環境下將風能轉化為電能并加以儲存，同時具有體積小、持久性好以及可無人操控等特點，克服了大型風力裝置的局限性，在環境保護、建筑安全以及交通系統中具有很高的實際應用價值.相比傳統風力發電裝置，壓電懸臂梁流致振動能量收集器不需要復雜的結構、安裝方便，且能量密度和功率譜密度相對較高.近年來，利用壓電材料從渦激振動中收集能量的研 究工作 得 以 廣 泛 開 展［1-3］.Allen等［4］設 計 了“eel（鰻魚）”能量收集器，但是未給出具體發電效率和發電功率的計算方法.Taylor等［5］使用鰻魚結構，模擬了壓電結構與流場的耦合作用，但是沒有給出輸出電壓和功率的計算方法.Kwon［6］采用多組鋯鈦酸鉛（PbZrTi，PZT）安裝在T 型結構上的能量收集方式，在15m／s的最高風速下獲得4mW的輸出功率.在壓電能量收集理論研究方面，Mehmood等［7］使用機電耦合方法得出壓電懸臂梁的能量收集能力與懸臂梁的振幅有關.Zhu等［8］針對壓電能量收集裝置（piezoelectric energy harvesting device，PEHD）的發電工作效率，通過對比三維及二維本構方程，得出懸臂梁發電模型的二維模型具有適用性，實現了數值模擬的降維.

渦激振動是一種流固交替耦合的自激振動過程.當旋渦脫落頻率和結構固有頻率相近時，會發生“鎖定”現象［9］，振動振幅顯著增大.Anagnostopoulos等［10］發現中等雷諾數下圓柱繞流渦激振動存在3個分支.在上支階段，流速較低時，自振頻率較小，此時自振頻率逐漸接近圓柱自身固有頻率，振幅逐漸增大，表現出“拍”現象，可視為過渡段；在鎖定階段，自振頻率與固有頻率發生耦合同步現象，振幅顯著增大，振動能與自振頻率較高；在下支階段，出現與上支類似的運動規律，但與上支不同的是，此時圓柱的振幅較小，自振主頻率增大并逐漸解除與固有頻率的耦合作用.利用“鎖定”時系統振動能較大的特點，Bernitsas等［11-12］提出了一種海洋清潔能源收集裝置（vortex-induced vibration aquatic clean energy，VIVACE），并在此基礎上利用計算流體力學（CFD）技術［13-14］對其進行能量收集評估，從而實現利用渦激振動原理收集海洋流動能，并給出海洋流動能收集的表達式［12］：

式中：P 為功率，ρ為流體密度，Cy為柱體表面升力，fo為自振頻率，ym為振動振幅，D 為圓柱直徑，L為圓柱體的長度，φ 為相位角.從式（1）可以看出，系統的輸出功率與圓柱的振動振幅有著直接關系.Wu等［13-14］利用OpenFOAM 針對單圓柱和多圓柱的渦激振動問題開發了求解器.Molino-Minero-Re等［15］提出了一種可用于在水槽中收集渦激振動能的旗幟狀柔性結構，并指出輸出功率與振幅呈正比.

上述研究大多未充分解決流體-結構-電路（流-固-電）三相耦合的問題，并認為系統輸出功率與振動振幅成正比關系.而渦激振動能量收集回路是通過加入載荷實現利用電路載荷進行能量收集，外界載荷對渦激振動系統具有負反饋作用，因此必須考慮電路與渦激振動的機電耦合效應.解決三相耦合問題的關鍵在于計算外界載荷對系統能量輸出的影響.

本研究通過在Matlab，中使用矩陣法計算載荷對渦激振動系統阻尼和固有頻率的影響，計算出電壓輸出的準穩態解，并以上述結果為基礎利用OpenFOAM 平臺計算圓柱渦激振動質量-彈簧-阻尼系統流固耦合響應.重點研究外界載荷對渦激振動系統振幅、電壓輸出以及功率輸出性能的影響，為渦激振動的能量收集提供理論基礎.

1 物理模型

1.1 質量-彈簧-阻尼系統

為描述渦激振動能量轉換模型中的剛性圓柱運動，取物理模型如圖1（a）所示，在圓柱兩端使用2根細長的PZT 壓電薄片進行支撐，將帶有電阻的電路連接到PZT 壓電懸臂梁上用于收集電荷.忽略圓柱橫向振動時壓電片的旋轉自由度，近似為二維單自由度質量-彈簧-阻尼（M-C-K）系統，如圖1（b）所示.其中M 為系統質量，C 為系統阻尼，K 為系統的彈簧剛度，無量綱來流速度取折合速度（reduced velocity）Ur＝U／（ωn·D）［9］，其中U 為來流風速，ωn為圓柱的固有頻率，D 為圓柱直徑.

1.2 網格劃分與邊界條件

本研究采用的流體計算域大小為50D×50D，圓柱位于流場正中心.邊界條件為速度進口，壓力出口，壁面采用無滑移邊界條件.計算區域上下邊界距離圓柱足夠遠，邊界對柱體周圍流場的影響可以忽略［16］，因此上下邊界采用與進口相同的邊界條件，從而保證流場流動的均勻性.控制邊界為

式中：Ω 為流固耦合面的外表面，V 為柱體的移動速度，VΩ為流固耦合面的移動速度.在流固耦合計算過程中，柱體在流場邊界范圍中上下移動.

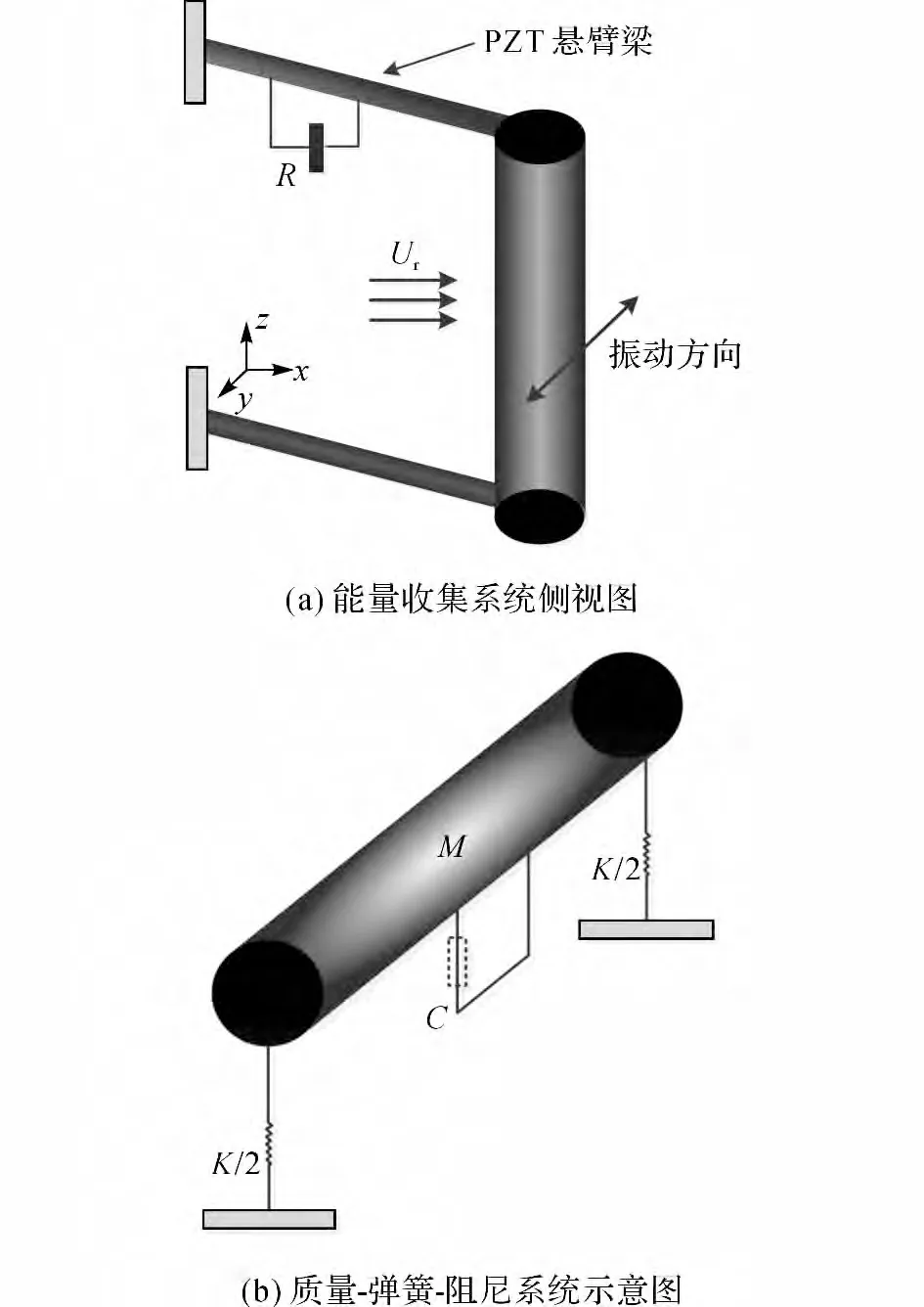
圖1 能量收集系統與振動系統Fig.1 Energy harvesting system and vibrating system

在計算渦激振動時，動網格的處理是影響計算效率及計算精度的重要因素之一.當渦激振動發生時，圓柱上下移動.同時，如圖2所示，計算區域網格隨圓柱發生整體運動，克服了傳統動網格的網格扭曲及變形的問題，從而提高計算效率和計算精度.采用Gambit生成四邊形網格，并在Re＝150時采用3種不同網格進行網格無關性驗證，結果如表1 所示，其中CL、CD、St分別為升力系數，阻力系數和斯特勞哈爾數.從表1可以看出，3種網格的計算結果較為吻合，因此選取網格密度為中等的網格來保證網格計算具有無關性.

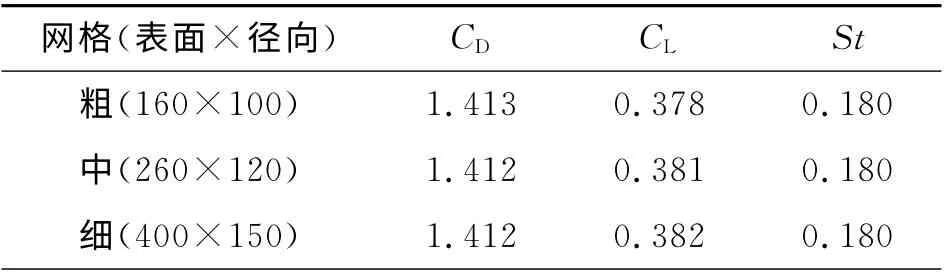
表1 網格無關性驗證（Re＝150）Tab.1 Neutrality authentication of meshes（Re＝150）

2 數學模型

為計算圓柱繞流外流場、渦激振動和電路回路3種不同量場的耦合過程，使用Navier-Stokes方程描述外界流場的流動，使用二階范德波爾方程描述單自由度M-C-K系統的渦激振動過程，最后使用高斯定律與振動方程的耦合形式描述機電耦合系統.

圖2 計算所用網格示意圖Fig.2 Schematic diagram of computational mesh

2.1 流固耦合模型

2.1.1 流動控制方程 圓柱繞流外部流場使用連續性方程和Navier-Stokes方程進行計算：

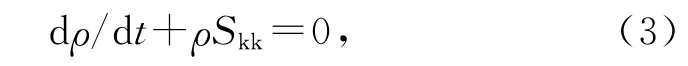
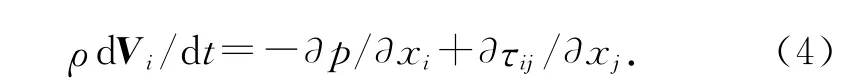
式中，p 為壓強，ρ為流體密度，Vi為流體速度矢量，τij為應力張量，Skk為應變率張量.

2.1.2 單自由度范德波爾振動方程 單自由度MC-K系統的運動控制方程由二階范德波爾方程表示：

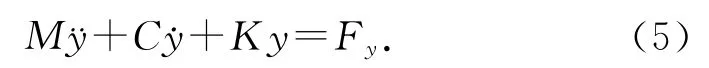
M、K、C 存在以下關系：

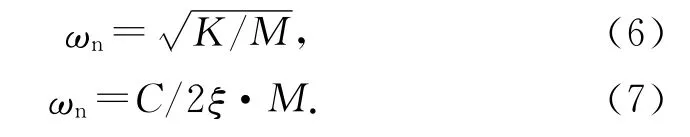
式中，Fy為垂直于來流方向的單位體積的流場力，ξ為無量綱阻尼比，y 表示柱體的振動位移，˙y和¨y分別表示位移的一、二階導數.將范德波爾方程與流體控制方程在求解器中同時求解，可以得到圓柱的動態振動響應.

2.2 機電耦合模型

2.2.1 阻尼及固有頻率求解 為了描述渦激振動電路中振幅與電壓的關系，引入高斯定律［17］進行理論推導.將高斯定律與式（5）的機電耦合變形方程聯立可得

式中：θ為機電耦合系數，Cp為電容系數，U 為電壓，R 為電阻.

式（8）、（9）分別考慮了渦激振動系統對電路輸出電壓的影響，同時考慮電路對振動系統的負反饋作用，即機電耦合.結合流場計算結果，即可實現流-機-電三相耦合.

為求解載荷對系統阻尼和固有頻率的影響，使用矩陣法求解二階非線性常微分方程式（8）的線性方程以及式（9）［18］.

令：X1＝y，X2＝˙y，X3＝U，將式（6）、（7）代入式（9）、（10）得

將上述方程組表示為矩陣形式：

式中：X＝［X1，X2，X3］T，

矩陣B（R）X 有3 個不同的特征值ki（i＝1，2，3）.Barrero-Gil等［18］指出：矩陣B（R）X 的特征值中前2個特征值與無電路振動系統類似，而第3個特征值則是機電耦合效應產生的結果，如壓電系統受到基礎或氣彈性激勵的作用，且為常實負數.k1、k2存在共軛關系，其中共軛解的實部（real）和虛部（imaginary）分別表示機電耦合系統中的阻尼和固有頻率；而由于k3是常實負數，本文在計算矩陣平凡解時僅考慮k1、k2的實部.

本研究選用文獻［7］中的單自由度振動機電耦合系統參數，如表2所示.

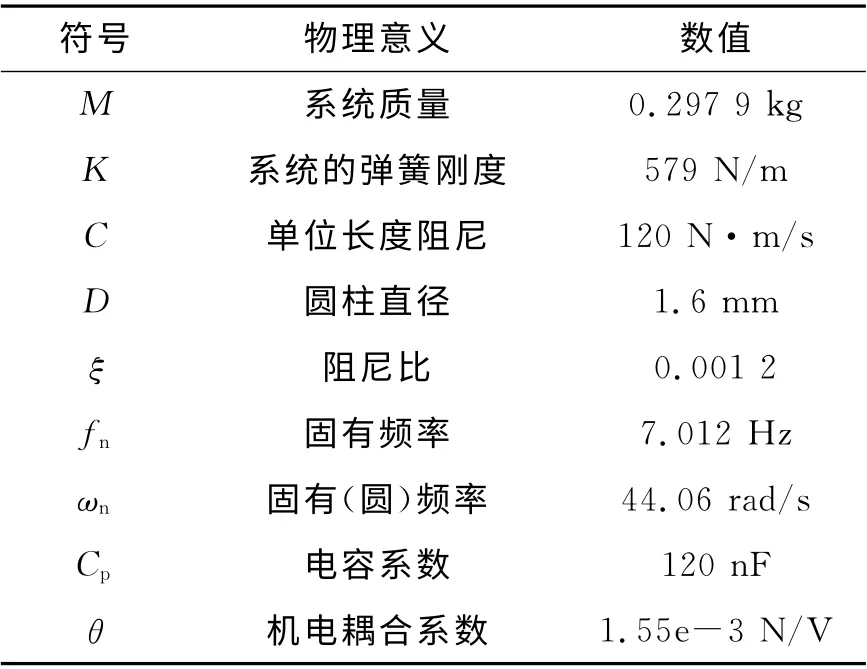
表2 單自由度振動機電耦合系統參數Tab.2 Parameters of free degree vibration electromechanical system

2.2.2 電壓輸出準穩態模型 采用Morse等［19］的準穩態模型描述渦激振動振幅，并用以計算隨時間變化振動能量的收集.在渦激振動處于同步性區域時，在能量收集系統中，柱體的振動振幅可以表示為正弦波形式：

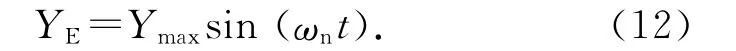
值得注意的是，電壓時程與振動振幅時程曲線是同步的，并不存在相位差.本文重點計算電壓輸出的峰值，將式（12）代入式（10），在Matlab中求出電壓的準穩態解解析式：

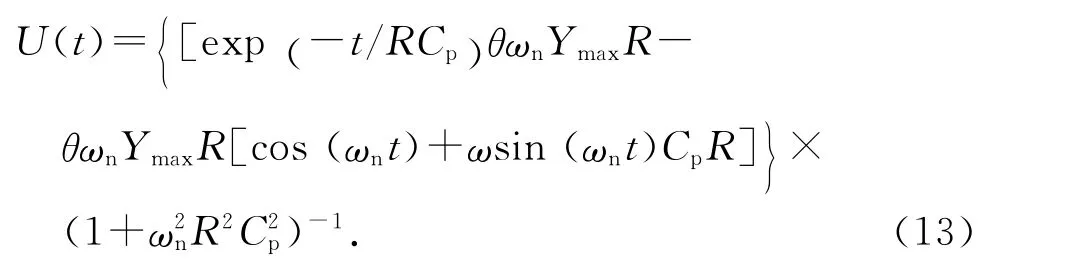
以上過程中的數學表達式包括流固耦合和機電耦合的求解過程.首先在OpenFOAM 中求解式（3）、（4），得出流場壓強p.壓強p 作用在柱體上產生流場力Fy.利用p 求解式（5），得到柱體產生的振動位移y.在壓力影響柱體運動的同時，柱體在流場中的振動反作用于流場從而影響流場分布，如此交替計算即解決流固耦合問題.在機電耦合模型中求解方程組（8）、（9），可得出系統阻尼C、固有圓頻率ωn的變化，而C 和ωn可以通過式（5）直接影響流固耦合計算中的P 和Fy.最后求得系統的振幅最大值Ymax，結合固有圓頻率計算結果ωn，使用式（13）可以得出系統電壓輸出的時程曲線，以上即為流-固-電三相耦合全過程.

3 流體求解器驗證

為了驗證本文流固求解器的正確性，采用文獻［10］中的實驗參數（繞流柱體的質量與柱體排開的流體質的比值m＊＝149，ξ＝0.001 2）進行渦激振動計算，并將結果與數值模擬的文獻結果［7，20-21］進行對比，如圖3所示.

當94＜Re＜140 時，本文的計算結果與文獻［7］、［20］及［21］中的數值模擬結果吻合較好.值得注意的是，本文得出的振幅值略小于文獻［10］中的實驗值，可能有2個方面的原因：一是本文采用的是無限大流動空間計算圓柱渦激振動，而文獻［10］的實驗過程中細長圓柱體的一部分在自由液面以上，存在自由液面的影響；二是文獻［10］的研究中雖然圓柱細長比比較大，但是在圓柱底端未安裝擋板，故實驗測得渦脫頻率偏小，渦激振動的上支過渡段會延遲進入鎖定階段.

圖3 本文方法的計算結果與其他文獻結果的對比Fig.3 Comparisons between results of present method and published data

4 計算結果及分析

4.1 系統阻尼和固有頻率特性

通過Matlab軟件求出機電耦合系統的阻尼和固有圓頻率，共軛解的實部和虛部隨電阻變化的計算結果如圖4所示.

圖4 矩陣共軛解實部、虛部隨電阻的變化Fig.4 Variations of real and imaginary parts of conjugate solution with load resistance

根據電路共軛解實部與虛部的關系，結合圖4可以看出，當載荷較小時，系統總阻尼較低.當R＜100kΩ 時，隨載荷的增大，系統總阻尼逐漸升高；當R＝100kΩ 左右時，系統總阻尼達到最大值.此外，隨載荷繼續增大，由于機電耦合阻尼的壓電分流阻尼效應（shunt damping effect）［22］，系 統 總 阻 尼 減小.在固有圓頻率方面，當R＜30kΩ 時，頻率基本保持在44rad／s；當R＞2 MΩ 時，頻率基本保持在50rad／s以下.系統固有圓頻率較為穩定，基本保持在44～50rad／s.

4.2 振幅變化特性

振動振幅是渦激振動機電耦合系統機電轉換系統能力的重要參數.為充分考察載荷對系統機電耦合的影響，考察載荷值范圍為1、10、100kΩ 以及1、10 MΩ 時振幅動態響應隨雷諾數的變化情況.

如圖5所示為當Re＝100時，不同載荷值對系統振動振幅的影響.由振幅時程曲線可以觀察到振幅幅值隨載荷值的變化而變化.當R＝1kΩ 時，振幅最大值為0.23D；當R＝10kΩ 時，振幅下降到y＝0.16D；當R＝100kΩ 時，振幅下降到0.09D；當R＝1MΩ 時，振動振幅增大；當R＝10MΩ 時，振幅最大值達到0.25D，超過當R＝1kΩ 時的峰值.振幅時程曲線的峰值總體呈現隨載荷的增大先減小后增大的趨勢.上述結果與圖4中渦激振動阻尼隨載荷的變化規律對應，系統阻尼越大，振動能越小，振幅相應越小.

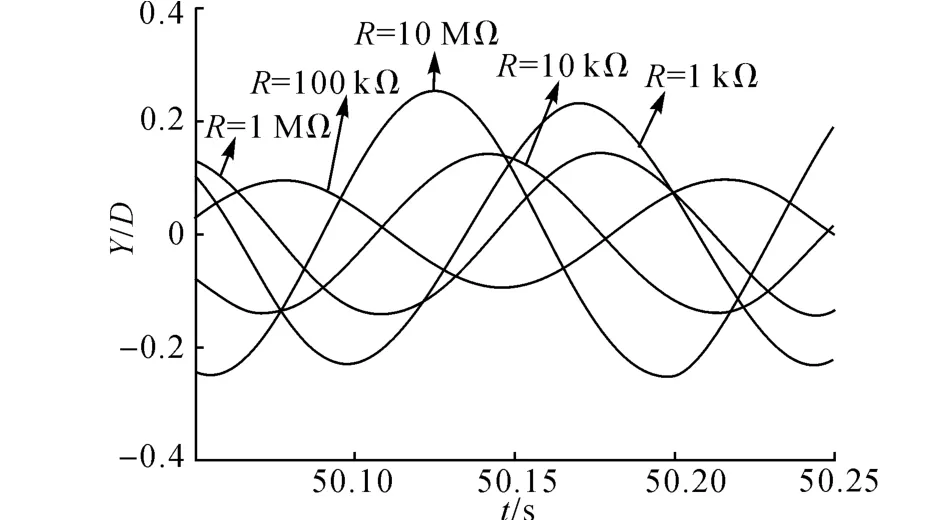
圖5 不同載荷下的振幅時程曲線（Re＝100）Fig.5 Time histories of amplitude with different load resistances when Re＝100

如圖6所示為當94≤Re≤115時不同載荷的振動幅值隨雷諾數的變化情況.當R＝1kΩ 時，振幅在柱體進入鎖定區后逐漸達到最大值0.31D.當Re增大時，振幅峰值開始下降，振幅曲線過渡到下支，振幅減小.當R＝10kΩ 時，鎖定區域振幅最大值只有0.19D；而當R＝100kΩ 時，系統阻尼增大到峰值，此時振幅最大值達到0.135D；當R＝1 MΩ 時，隨振動阻尼減小，振幅達到0.21D；當R＝10 MΩ時，振幅最大值達到0.34D.可見隨載荷值的增大，振幅曲線先增大后減小.當98＜Re＜103 時，系統具有較大振幅值.

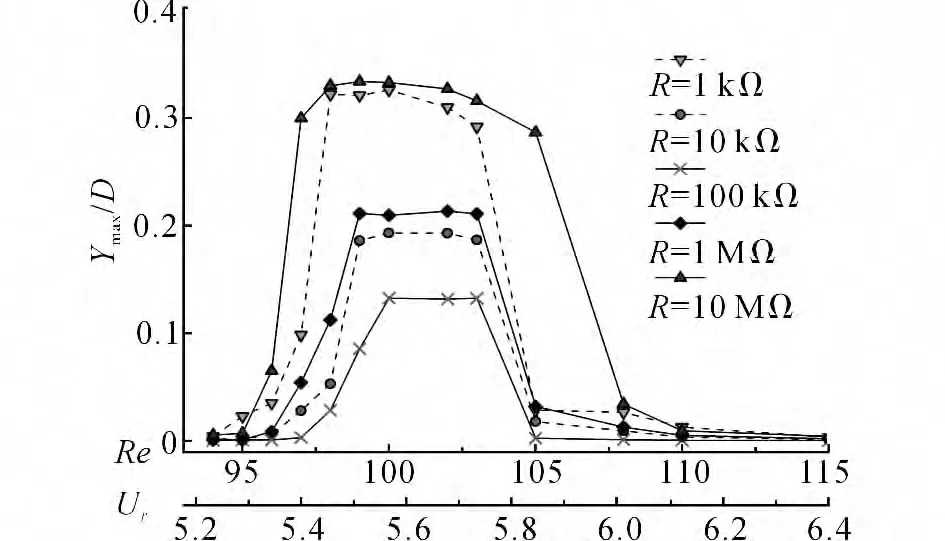
圖6 圓柱渦激振動在不同載荷和雷諾數下的振幅幅值變化Fig.6 Changes of amplitude of the vortex-induced vibration under different load resistances and Reynolds numbers

在鎖定區域方面，當R＝1kΩ 時，系統在Re＝98附近開始進入鎖定區域；當R＝10kΩ 時，圓柱的鎖定區域開始出現“滯后”現象，當Re＝99時，振幅曲線由上支過渡到鎖定區域，原因是載荷使系統的固有頻率和阻尼發生了改變；當R＝100kΩ 時，鎖定區域較窄，當R＝100 左右時，系統進入鎖定區域；當Re＝1MΩ 時，可以觀察到與振幅曲線類似的規律，鎖定區域變大，當Re＝98 時，系統進入鎖定范圍；當R＝10 MΩ、Re＝96時，系統開始進入鎖定范圍.綜上所述，振幅曲線的鎖定范圍會在較大和較小載荷值下變得較寬，并經過先減小后增大的過程.

4.3 電壓輸出變化特性

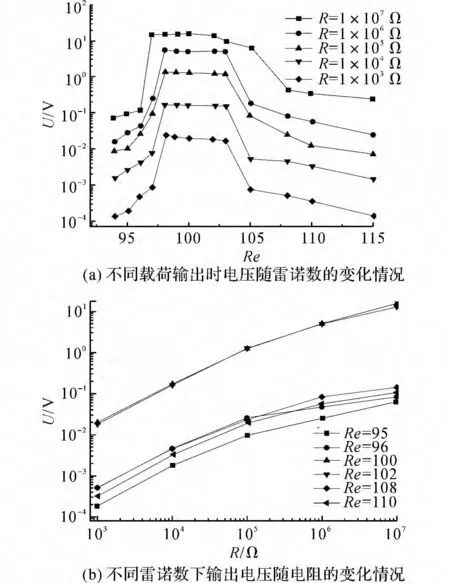
圖7 圓柱渦激振動系統的輸出電壓變化情況Fig.7 Changes of voltage output of vortex-induced vibrating cylind

圖7（a）表示不同載荷下系統電壓輸出的均方根值（即有效值）對Re 的變化趨勢.隨著載荷值的增加，系統的輸出電壓逐漸增大，當R＝10 MΩ，Re＝96時出現最大值.當Re增大時，電壓值在鎖定區域上基本保持穩定.隨著載荷值的增大，電壓曲線的鎖振區域漸漸增大并覆蓋到更高雷諾數.如當R＝1kΩ時，在Re＝98附近才開始進入鎖定區域，并在Re＝103附近退出鎖定區域；而當R＝10 MΩ時，在Re＝96時已經進入鎖定狀態，在Re＝105左右時退出鎖定區域.此外，從電壓有效值曲線中可以得出，下支的電壓值要稍高于上支的電壓值.圖7（b）表示不同雷諾數下系統輸出電壓的有效值隨著載荷的變化規律.為便于分析討論，每個載荷分別列出3個分支下的2個雷諾數工況.從圖7（b）可以看出，上支與下支的電壓輸出大致相近，且具有相似的變化規律.在所有的載荷下，電壓輸出的最大值都處于同步性區域中，增大系統載荷可以提升系統的電壓輸出.當R＞100kΩ 時，電壓的增長幅度開始降低.當98＜Re＜103時，系統具有較高的輸出電壓.

4.4 功率輸出變化特性

求得系統的輸出電壓后，以電壓計算結果為基礎，使用式（14）對功率進行計算［23］：

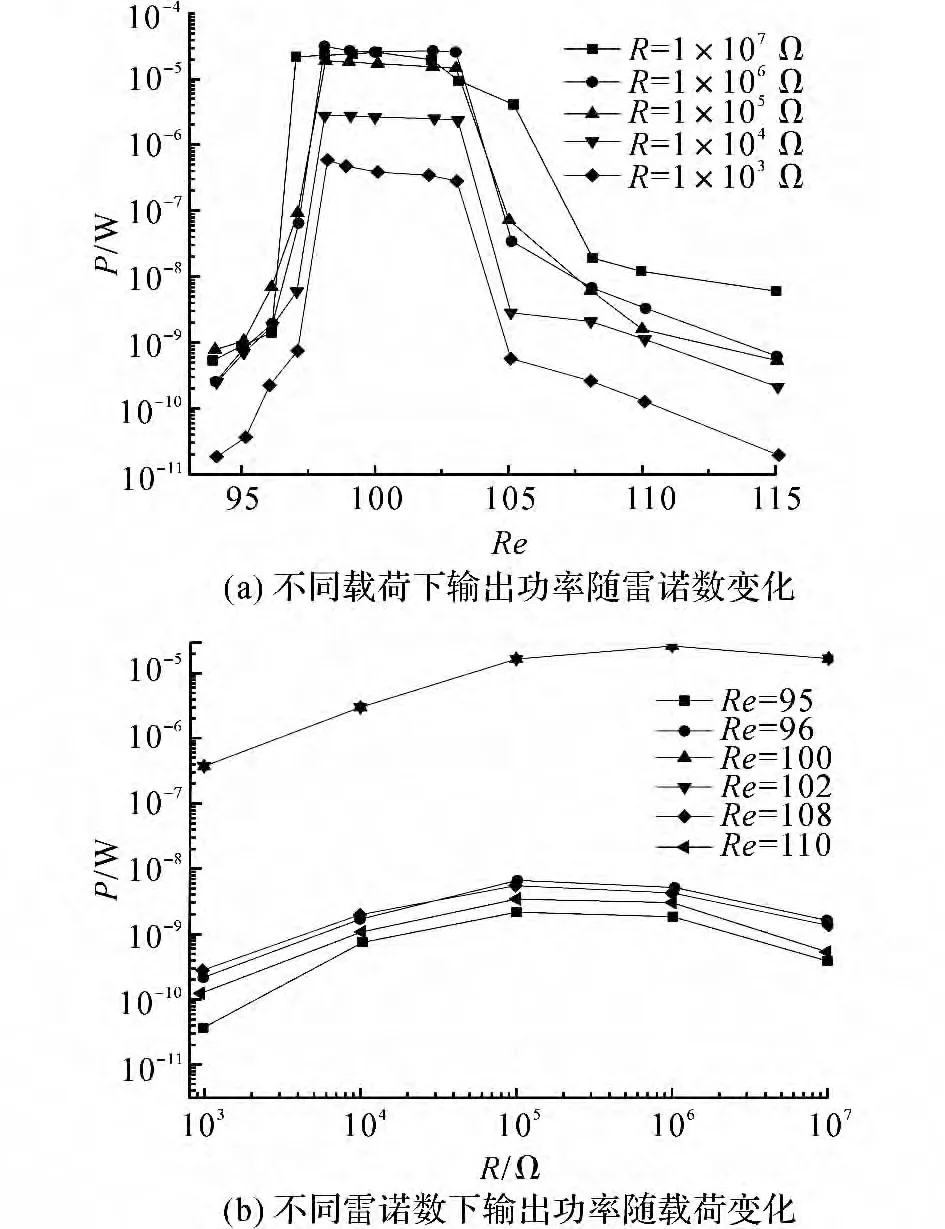
圖8 圓柱渦激振動系統的輸出功率變化情況Fig.8 Changes of power output of vortex-induced vibrating system

圖8（a）表示不同載荷下系統功率輸出P 對Re的變化曲線.功率輸出的最大值出現在鎖定區域內，但是與輸出電壓曲線不同的是，功率輸出會隨著載荷值的增大先增大后減小，從圖8（b）可以更好地觀察到這一點.圖8（b）表示不同雷諾數下輸出功率對不同載荷的變化曲線.當R 從1kΩ 增加到100kΩ時，功率逐漸增大，而且當R＝1 MΩ 時存在最大值.當R＝1 MΩ 時，由于分流阻尼效應此時系統的阻尼較大，振動振幅較小，說明當最大振幅出現時，并沒有出現最大功率，即系統功率輸出與振動振幅并不成正比關系.但是當98＜Re＜103 時，系統具有較高的功率輸出，渦激振動能量轉換效率較高.此項結論與文獻［12］、［15］中未考慮三相耦合的計算結果不同.

5 結 論

本研究從解決渦激振動能量轉換中的三相耦合問題出發，采用數值研究方法獲得了系統的阻尼與固有頻率隨外界載荷的變化規律，導出系統電壓輸出的準穩態解析式，以及渦激振動能量轉換系統中振動振幅、電壓和功率隨不同外界載荷的變化規律.主要結論如下：

（1）當外界載荷增大時，系統阻尼先增大后減小，固有頻率基本不變.

（2）振動最大值和振幅曲線的鎖振區域會隨著載荷值的增加先減小后增大.

（3）電壓輸出有效值隨載荷的增大而增大，同時，當載荷增大時，電壓曲線的鎖振區域會相應增大，并覆蓋到更高的雷諾數范圍.

（4）系統輸出功率隨著載荷的增大先增大后減小，最大輸出功率并不在最大振動振幅處出現.當98＜Re＜103時，系統具有較高的功率輸出，可以實現較高的渦激振動能量轉換效率.

（

）：

［1］GAO X，SHIH W H，SHIH W Y.Flow energy harvesting using piezoelectric cantilevers with cylindrical extension［J］.，IEEE Transactions on Industrial Electronics，2013，60（3）：1116-1118.

［2］XU B，CHEN X.Liquid flow-induced energy harvesting in carbon nanotubes：a molecular dynamics study［J］.Physical Chemistry Chemical Physics，2012，15（4）：1164-1168.

［3］LIU H，TAY C J，QUAN C，et al.Piezoelectric MEMS energy harvester for low-frequency vibrations with wideband operation range and steadily increased output power［J］.Journal of Microelectromechanical Systems，2011，20（5）：1131-1142.

［4］ALLEN J J，SMITS A J.Energy harvesting eel［J］.Journal of Fluids and Structures，2001，15（3）：629-640.

［5］TAYLOR G W，BURNS J R，KAMMANN S M，et al.The energy harvesting eel：a small subsurface ocean／river power generator［J］.IEEE Journal of Oceanic Engineering，2001，26（4）：539-547.

［6］KWON，S D.A T-shaped piezoelectric cantilever for fluid energy harvesting［J］.Applied Physics Letters，2010，97（16）：164102（1-3）.

［7］MEHMOOD A，ABDELKEFI A，HAJJ M R，et al.Piezoelectric energy harvesting from vortex-induced vibrations of circular cylinder［J］.Journal of Sound and Vibration，2013，332（19）：4656-4667.

［8］ZHU M L，LEIGHTON G.Dimensional reduction study of piezoelectric ceramics constitutive equations from 3-D to 2-D and 1-D ［J］.IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control，2008，55（11）：2377-2383.

［9］丁文鏡.自激振動［M］.北京：清華大學出版社，2009.

［10］ANAGNOSTOPOULOS P，BEARMAN P.Response characteristics of a vortex-excited cylinder at low reynolds numbers［J］.Journal of Fluids and Structures，1992，6（1）：39-50.

［11］BERNITSAS M M，RAGHAVAN K，BEN-SIMON Y，et al.VIVACE （vortex induced vibration aquatic clean energy）：a new concept in generation of clean and renewable energy from fluid flow［J］.Journal of Offshore Mechanics and Arctic Engineering，2008，130（4）：041101.

［12］RAGHAVAN K，BERNITSAS M M.Experimental investigation of reynolds number effect on vortex induced vibration of rigid circular cylinder on elastic supports［J］.Ocean Engineering，2011，38（5）：719-731.

［13］WU W，BERNITSAS M M，MAKI K.RANS simulation vs.experiments offlowinduced motion of circular cylinder with passive turbulence control at 35，000≤Re≤130，000［C］∥Proceedings of ASME 2011 30th International Conference on Ocean，Offshore and Arctic Engineering.Rotterdam：ASME，2011：733-744.

［14］DING L，BERNITSAS M M，KIM E S.2-D URANS vs.experiments of flow induced motions of two circular cylinders in tandem with passive turbulence control for 30，000≤Re≤105，000［J］.Ocean Engineering，2013，72：429-440.

［15］MOLINO-MINERO-RE E，CARBONELL-VENTURA M，FISAC-FUENTES C，et al.Piezoelectric energy harvesting from induced vortex in water flow［C］∥Proceedings of Instrumentation and Measurement Technology Conference（I2MTC）.Graz：IEEE，2012：624-627.

［16］丁林，張力，楊仲卿.高雷諾數時分隔板對圓柱渦致振動的影響［J］.機械工程學報，2013，49（14）：133-139.DING Lin，ZHANG Li，YANG Zhong-qing.Effect of splitter plate on vortex-induced vibration of circular cylinder at high reynolds number［J］.Chinese Journal of Mechanical Engineering，2013，49（14）：133-139.

［17］BARRERO-GIL A，ALONSO G，SANZ-ANDRES A.Energy harvesting from transverse galloping［J］.Journal of Sound and Vibration，2010，329（14）：2873-2883.

［18］BARRERO-GIL A，SANZ-ANDRéS A，ALONSO G.Hysteresis in transverse galloping：the role of the inflection points［J］.Journal of Fluids and Structures，2009，25（6）：1007-1020.

［19］MORSE T L，WILLIAMSON C H K.Steady，unsteady and transient vortex-induced vibration predicted using controlled motion data［J］.Journal of Fluid Mechanics，2010，649：429-451.

［20］YANG J，PREIDIKMAN S，BALARAS E.A strongly coupled，embedded-boundary method for fluid-structure interactions of elastically mounted rigid bodies［J］.Journal of Fluids and Structures，2008，24（2）：167-182.

［21］SCHULZ K W，KALLINDERIS Y.Unsteady flow structure interaction for incompressible flows using deformable hybrid grids［J］.Journal of Computational Physics，1998，143（2）：569-597.

［22］李寧，程禮.壓電分流阻尼的虛擬實現［J］.空軍工程大學學報：自然科學版，2008，9（4）：59-63.LI Ning，CHENG Li.Virtual implemention method of piezoelectric shunt damping［J］.Journal of Air Force Engineering University：Natural Science Edition，2008，9（4）：59-63.

［23］AKAYDIN H D，ELVIN N，ANDREOPOULOS Y.Energy harvesting from highly unsteady fluid flows using piezoelectric materials［J］.Journal of Intelligent Material Systems and Structures，2010，21（13）：1263-1278.