空氣對預應力薄膜結構模態的影響

陳宇峰，陳務軍，邱振宇，趙 兵

（上海交通大學 空間結構研究中心，上海200240）

空間薄膜陣面結構重量輕、抗振性好、展開可靠性高且費用低，可以用于制作深空探索太陽帆以及雷達薄膜天線，空間薄膜結構剛度主要取決于邊緣幾何外形和預應力水平［1-4］.開展薄膜結構自振特性研究可以預測振動形式及預防共振.在數值模擬時通常沒有空氣，并且在真空罐中測薄膜陣面結構模態成本較高.因此，研究空氣附加質量對結構模態的影響可以為薄膜結構模態測試和校驗提供分析方法.薄膜結構模態分析與測試仍然是目前的研究熱點之一，Xiao等［5-8］對薄膜結構的預應力導入方式及預應力薄膜結構模態影響因素進行了分析和實驗.Dowell等［9］利用行波理論推導了有限寬無限長薄板的附加質量.Minami［10］基于勢流理論，得出空氣密度及模型尺寸與矩形平面薄膜在空氣中的附加質量直接相關.Yadykin等［11］總結了附加質量對薄板影響的研究結果，并對流體中平面柔性薄板附加質量影響進行了數值研究，采用薄翼理論（thin aerofoil theory）計算了一個懸臂板面的壓力分布，并計算了前10 階模態的附加質量大小.Li等［12-13］利用真空箱測試薄膜在不同密度空氣中的振動特性，研究了薄膜振動的附加質量影響因素和規律，給出了模型附加質量分布模型，根據簡化模型可以方便確定模型在不同振型下附加質量取值方式.高海健等［14］研究了薄膜充氣管的預應力導入及考慮空氣附加質量模態計算.筆者［15］借助ABAQUS軟件，探討了柔性飛艇在無約束狀態下單元模型、拼接縫、不均勻質量分布、內外壓差、尺寸以及飛艇周圍空氣附加質量對飛艇主氣囊自振特性的影響.目前，采用施加溫度載荷的方式導入薄膜結構預應力，并通過理論或實驗來確定流體對結構物的附加質量，利用附加質量有限元法考慮流體與結構的耦合模態.利用流固耦合的勢流體原理分析空氣對預應力薄膜結構模態影響的研究較少.結構在真空狀態下的模態稱為干膜態，考慮結構周圍接觸介質影響時的模態稱為濕模態.

本研究利用ADINA 軟件對在2種不同預應力引入方式下的預應力薄膜結構模態進行研究；在此基礎上利用流固耦合的勢流體原理，分析空氣對預應力薄膜的影響；利用自制的雙軸張拉設備開展乙烯-四氟乙烯共聚物（ethylene-tetra-fluoro-ethylene，ETFE）的模態實驗，并對數值模擬結果進行驗證.

1 薄膜陣面模態分析方法

薄膜預應力水平直接影響預應力薄膜結構的剛度，因此預應力薄膜結構的模態需要考慮預應力的影響.結構自振控制方程為

式中：Μ 為質量矩陣，Κ 為結構總剛度矩陣，Κe為單元剛度矩陣，u為節點振幅向量.

對式（1）進行正則化，可得結構廣義特征方程：

式中：ω 為圓頻率，φ為特征向量

1.1 薄膜結構干模態分析

圖1 薄膜結構模型Fig.1 Structure of planar membrane

首先研究預應力對薄膜結構模態的影響.以如圖1所示的模型作為對象，分析不同預應力導入方式對薄膜結構模態的影響.目前，常用的薄膜結構預應力導入方式有2種：方式A——直接對零應力態的薄膜結構模型施加初應力；方式B——通過對薄膜結構施加溫度荷載導入預應力.薄膜結構模型材料的密度為1 700kg／m3，彈性模量為810 MPa，泊松比為0.3.對模型四周3個位移自由度都施加約束.對模型進行一步靜力分析來查看膜面的預應力是否成功導入，如圖2所示.

圖2 薄膜導入應力分布Fig.2 Stress distribution of pre-stressed model

采用ADINA 8.7作為分析工具，分析過程如下.

預應力導入方式A：1）建立薄膜結構數值模型，賦予材料性質及截面特性；2）將數值模型劃分網格，膜面采用3D 板應力（膜）單元；3）考慮薄膜大變形的幾何非線性，直接對薄膜結構單元的膜面賦予初應力，程序自動轉換成初應變；4）利用蘭索斯法對預應力薄膜結構模態進行數值計算分析.

1）、2）預應力導入方式B：與方式A 完全相同；3）考慮薄膜大變形的幾何非線性，對膜面施加溫度場荷載并進行一步靜力分析；4）最后利用蘭索斯法對預應力薄膜結構模態進行數值計算分析.

薄膜結構模型在2種預應力導入方式下的數值分析結果分別如圖3及表2所示.圖3為薄膜結構振型，表1為薄膜結構頻率.可以看出，在2種預應力導入方式下的振型及頻率完全一致.

表1 2種預應力導入方式下的模型頻率Tab.1 Frequencies of model under two prestress introducing methods Hz

圖3 薄膜結構模型前4階振型圖Fig.3 The first four modes of membrane structure model

1.2 空氣中薄膜結構模態分析

考慮流體對結構模態影響的理論在船舶、潛艇及水利工程等領域研究較多，由于水的密度大，對這類結構的影響較大.空氣對預應力薄膜結構的影響研究還較少.

1.2.1 流固耦合基本原理 設流體是均勻、無黏、無旋的理想流體，僅限于討論小撓動情況.理想不可壓縮流體小擾動的基本方程［10］為

式中：P 表示壓力，▽表示拉普拉斯方程.

根據式（4）并利用無限流遠邊界條件建立流體的有限元方程，結合結構的運動方程，得到附加質量矩陣［16］：

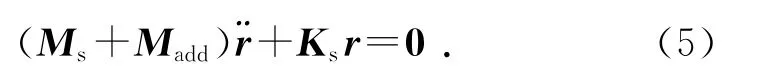
式中：Ms為結構質量矩陣，Madd為流體附加質量矩陣，r為結構位移矢量，Ks為結構剛度矩陣.

1.2.2 數值模型及結果分析 研究空氣對預應力ETFE薄膜結構模態的影響.模型與干模態的模型相同，模型有限元模型如圖4所示，空氣密度取1.293kg／m3.采用方式A 導入預應力并進行模態分析.薄膜結構的空氣范圍為邊長為1.5 m 的立方體，薄膜結構——空氣的有限元模型如圖5所示.將數值模型劃分網格，膜面采用3D 板應力（膜）單元，流體采用線性三維勢流體單元模型（3D-Fluid）.為了保證薄膜能與流體協同工作，流體與膜面接觸的2個面網格大小相同，節點相對應，通過Face-link使得流體與膜面接觸的2個面協同工作；3）考慮薄膜大變形的幾何非線性，直接對薄膜結構單元的膜面賦予初應力，程序自動轉換成初應變；4）利用蘭索斯法對預應力薄膜結構模態進行數值分析.從表2可以看出，空氣對預應力薄膜的模態有著顯著影響，假定干膜態的頻率為基準值，則考慮空氣附加質量后，薄膜的自振基頻大約減小40%.

圖4 薄膜結構有限元模型Fig.4 FEM model of membrane structure

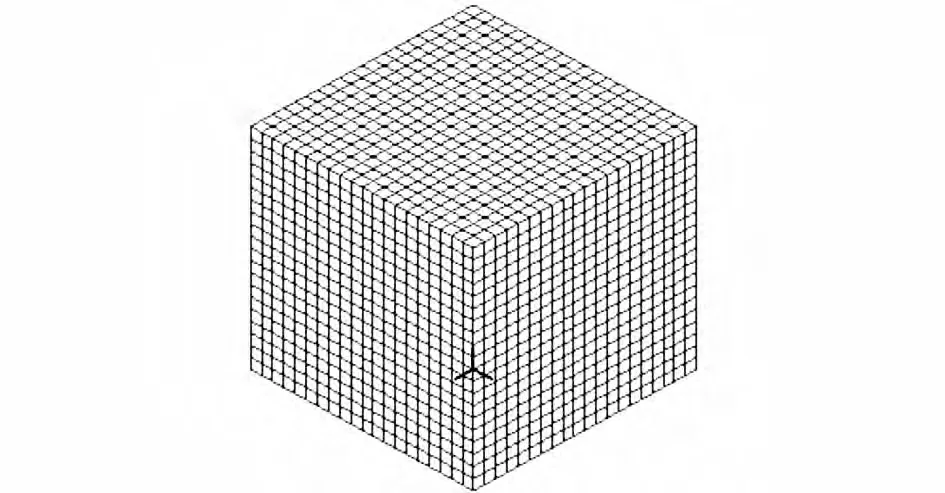
圖5 空氣有限元模型Fig.5 FEM model of air

表2 薄膜模型頻率Tab.2 Frequencies of membrane model

2 薄膜結構模態實驗

ETFE薄膜在低應力階段呈線彈性，各向同性，便于表征薄膜在空氣中的振動力學行為，因此選取ETFE張拉薄膜進行膜態實驗.首先研制一套雙軸張拉的實驗裝置，通過該實驗裝置對ETFE 薄膜結構施加預應力.采用不同頻率聲波對薄膜施加激勵，利用Polytec掃描式激光測振儀測振和模態辨識，測量原理是利用激光的多普勒效應.

2.1 雙軸拉伸實驗裝置

薄膜模態測試裝置如圖6所示，測試實驗裝置由試件固定鋼框架、拉力施加設備以及拉力控制設備等組成.通過拉力施加和控制設備獲得不同膜面應力水平的狀態.

圖6 ETFE薄膜模態測試實驗圖Fig.6 Image of modal testing for ETFE membrane

2.2 ETFE薄膜試件

實驗采用ETFE薄膜的厚度為150.0μm.ETFE薄膜試件定位尺寸為500.0mm×500.0mm，在定位線設置Φ8PE棒，薄膜焊接雙向包邊繩套，焊縫寬度為10.0mm.試件的四角內切34.5mm 凹角，并設5.0mm半徑圓倒角.試件如圖7所示.

圖7 ETFE薄膜雙軸拉伸實驗裝置Fig.7 Biaxial extension specimen photo of ETFE foil

2.3 實驗過程

ETFE薄膜模態實驗是一個精細、復雜的過程，主要步驟包括：

1）拉力施加設備的校驗標定，實驗準備；

2）實驗試件安裝與固定；

3）膜面預張拉采用先預張緊，然后卸載，并將拉力計調零，張力對稱；

4）實驗加載使ETFE 膜面獲得預應力，按照1∶1比例同步加載；

5）對薄膜結構均勻噴灑銀光粉，能使測振儀發射的激光束有效反射，在進行模態測試時，采用聲波對薄膜進行激振，用激光測振儀測振和模態辨識，并記錄；

6）卸載后，重復張拉，再次采用聲波薄膜振動，用激光測振儀測振和模態辨識.

2.3 實驗現象與實驗數據結果

為了得到均勻的膜面預應力狀態，通過3次重復加載，消除非一致性問題；施加荷載，將2個拉力計合力F 轉化為應力σ0，合力除以ETFE 薄膜試件有效截面積轉化為應力，使薄膜結構達到預定的預應力；利用激光測振儀測試模態.實驗的難點在于獲取均勻膜面的預應力，由圖8 可以看出，數值模擬的薄膜結構振型和測試結果完全一致.如表3所示，假設實驗測試的頻率為參考值，則ETFE 模型不考慮空氣影響時的數值模擬與實驗值的誤差在50%左右；考慮空氣影響時，兩者的誤差小于10%.由表3可以看出，空氣對預應力薄膜的模態有顯著影響，因此在分析空氣中薄膜結構的模態時，不能忽略空氣的作用.

圖8 ETFE測試模型的模擬及實驗振型Fig.8 The vibration shape of simulation and test for ETFE film

表3 ETFE測試模型的干濕頻率誤差分析Tab.3 Error analysis of dry and wet modal shape of ETFE test model

3 結 語

對于預應力薄膜結構直接對膜面賦予初應力后提取模態和通過降溫法引入預應力計算再提取模態結果是一致的.預應力薄膜模態實驗驗證了基于勢流體原理模擬空氣對預應力薄膜模態影響這一數值方法的合理性.空氣對預應力薄膜的模態有顯著影響，其影響的大小與薄膜材料以及空氣密度相關.本研究提出的數值模擬方法對揭示空間柔性預應力薄膜結構的自振特性具有重要參考價值.

（

）：

［1］LAI C Y，YOU Z，PELLEGRINO S.Shape of deployable membrane reflectors［J］.Journal of Aerospace Engineering，1998，11（3）：73-80.

［2］MALONE P K，WILLIAMS G T.Lightweight inflatable solar array［J］.Journal of Propulsion and Power，1996，12（5）：866-872.

［3］NABOULSI S.Investigation of geometric imperfection in inflatable aerospace structures［J］.Journal of Aerospace Engineering，2004，17（3）：98-105.

［4］WONG Y W，PELLEGRINO S.Wrinkled membranes part I：experiments［J］.Journal of Mechanics of Materials and Structures，2006，1（1）：1-23.

［5］XIAO W W，CHEN W J，FU G Y.Wrinkle analysis of the space planar film reflect-array［J］.Journal of Zhejiang University：Science A，2011，12（1）：24-32.

［6］XIAO W W，CHEN W J，FU G Y.Wrinkle analysis of the inflatable antenna［J］.Journal of Shanghai Jiao Tong University：Science，2011，16（1）：24-33.

［7］肖薇薇，陳務軍，付功義.空間薄膜陣面預應力導入效應及影響因素［J］.宇航學報，2010，31（3）：845-849.XIAO Wei-wei，CHEN Wu-jun ，FU Gong-yi.Prestressed introduction effects and influence factors investigation for the space plannar film reflect-arry［J］.Journal of astronatics，2010，31（3）：845-849.

［8］肖薇薇.空間充氣可展薄膜天線結構分析與力學特性研究［D］.上海：上海交通大學，2010：32-44.XIAO Wei-wei.Structural analysis procedures and me-chanical behavior of the space inflatable film antenna［D］.Shanghai：Shanghai Jiao Tong University，2010：32-44.

［9］DOWELL E，DUGUNDJI J，PERKIN B.Subsonic flutter of panels on continuous elastic foundations［J］.Journal of American Institute of Aeronautics and Astronautics，1963，1（5）：1146-1154.

［10］MINAMI H.Added mass of a membrane vibrating at finite amplitude［J］.Journal of Fluids and Structures，1998，12（7）：919-932.

［11］YADYKIN Y，TENETOV V，LEVIN D.The added mass of a flexible plate oscillating in a fluid［J］.Journal of Fluids and Structures，2003，17（1）：115-123.

［12］LI Y Q，WANG L，SHEN Z Y，et al.Added mass estimation of flat membranes vibrating in still air［J］.Journal of Wind Engineering and Industrial Aerodynamics，2011，99（8）：815-824.

［13］王磊，李元齊，沈祖炎.薄膜振動附加質量實驗研究［J］.振動工程學報，2011，24（2）：125-132.WANG Lei，LI Yuan-qi，SHEN Zu-yan.Experimental investigation on the added mass of membranes vibrating in air［J］.Journal of Vibration Engineering，2011，24（2）：125-132.

［14］陳宇峰，陳務軍，何艷麗，等.柔性飛艇主氣囊干濕模態分析與影響因素［J］.上海交通大學學報，2014，48（2）：234-238.CHEN Yu-feng，CHEN Wu-jun，HE Yan-li，et al.Dry and wet modal analysis and evaluation of influence factors for the flexible airship envelop［J］.Journal of Shanghai Jiao Tong University，2014，48（2）：234-238.

［15］高海健，陳務軍，付功義.預應力薄膜充氣梁模態的分析方法及特性［J］.華南理工大學學報，2010，38（7）：135-139.GAO Hai-jian，CHEN Wu-jun，FU Gong-yi.Modal analysis method and modal behavior of pre-stressed inflatable fabric beam［J］.Journal of South China University of Technology，2010，38（7）：135-139.

［16］高海健.大型平流層空間平臺柔性飛艇結構分析理論與特性研究［D］.上海：上海交通大學，2010：86-107.GAO Hai-jian.Structure analysis theory and performance research for large flexible airship of stratospheric platform［D］.Shanghai：Shanghai Jiao Tong University，2010：86-107.