預制裝配式板梁橋的模型修正方法

周正茂， 袁桂芳， 田清勇

(上海同豪土木工程咨詢有限公司，上海 200092)

利用現場實測數據修正結構的有限元模型，使修正后結構分析參數與試驗值趨于一致，稱為結構模型修正［1］.近年來，模型修正技術在橋梁領域逐漸成為研究熱點.早期研究以單根梁為主，如懸臂梁［2］、簡支梁［1，3］等，現在已逐步擴展到整橋，如 T構帶掛孔梁橋［4］、連續梁橋［5-7］、鋼桁梁橋［8］、系桿拱橋［9-10］、斜拉橋［11-15］和懸索橋［16］等.這些研究極大地促進了模型修正方法在橋梁工程中的應用.

目前模型中參數修正的對象是主要構件的設計參數如彈性模量等，對于連接構件的參數修正則研究較少.連接構件在預制裝配式橋梁中扮演著重要角色，一方面，連接構件如空心板梁橋中的鉸縫、T梁橋或小箱梁橋中的橫隔梁等對橋梁橫向受力的分配起著重要作用;另一方面，這些構件均為易損構件，它們的損壞將改變橋梁的受力狀態，使之與設計不符.因此，連接構件設計參數的修正對于掌握預制裝配式橋梁的受力狀態至關重要.但連接構件不易模擬，目前關于預制裝配式橋梁模型修正的研究也非常少.

朱張峰等研究了5片小箱梁組成的裝配式簡支梁橋的模型修正問題，其中橋梁橫向剛度的修正通過改變橋面板的彈性模量或厚度模擬［17］.該方法用于模擬橫隔梁效果較好，但用于模擬鉸縫則困難較大.在空心板梁橋力學模型中，鉸縫作為鉸來模擬，它既無厚度參數，也無彈性模量參數，因此，無法將文獻［17］的方法直接應用于空心板梁橋.周正茂等提出了鉸縫剛度的概念，假設鉸縫受力后會產生相對位移，且該位移與鉸縫剪力成正比［18］.在此基礎上，建立了可以考慮鉸縫損傷的模型，通過該模型可以評價鉸縫的損傷程度.但該模型只考慮了鉸縫損傷，并未考慮板梁受損，也不適用于橋上有防撞護欄、隔離墩和橋面鋪裝等附屬結構的情況，工程應用受到一定限制.

本文中嘗試建立空心板梁橋的結構修正模型，不僅能模擬鉸縫損傷，通過定義板的抗彎剛度和抗扭剛度修正系數，還能反映板梁損傷和附屬結構的貢獻.該模型既能反映空心板梁橋可能受到的各種損傷，又能克服一般力學模型模擬附屬結構的困難.為檢驗模型的正確性，采用數值方法模擬一座單跨空心板梁橋的荷載試驗，考察了該模型的反演誤差.

1 板梁橋的結構模型修正

1.1 模型假設與板邊位移方程

提出的模型是在鉸接板梁法的基礎上改造而成，所以，基本假設同鉸接板梁法［19］:荷載、剪力和位移沿縱向均為半波正弦分布;板間豎向剪力只靠鉸縫傳遞;板梁橫向為剛性等.文獻［18］中假設鉸縫相對位移與鉸縫剪力成正比，已得到試驗數據支持［20］，這里繼續沿用.關于板剛度，假設板剛度的變化由板的抗彎剛度和抗扭剛度體現.

鉸接板梁法模型見圖1.對編號及方向作如下規定:板的編號自左至右分別為1，2，…，n;鉸縫編號自左至右分別為1，2，…，n－1;鉸縫剪力以圖示方向為正，相對位移正方向與剪力正方向相反;板上荷載以圖示方向為正，其橫向偏心以板中心為原點，向右為正;板位移的正方向與板上荷載的正方向相同.

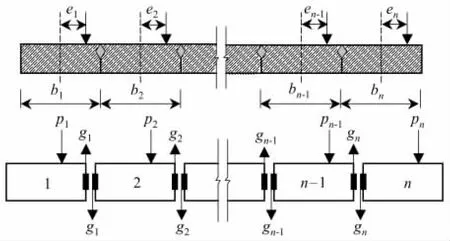
圖1 鉸接板橋計算模型Fig.1 Mechanical model of hinged slab bridge

于是，板左側和右側的位移方程分別為:

1.2 δik和 fij的計算

鉸縫剪力對板的作用可等效為一個作用在板中心的荷載和一個扭矩.圖2為單位鉸縫剪力與板兩邊位移的關系.

根據圖2，單位鉸縫剪力和單位板上荷載在第i塊板左側產生的位移分別為:

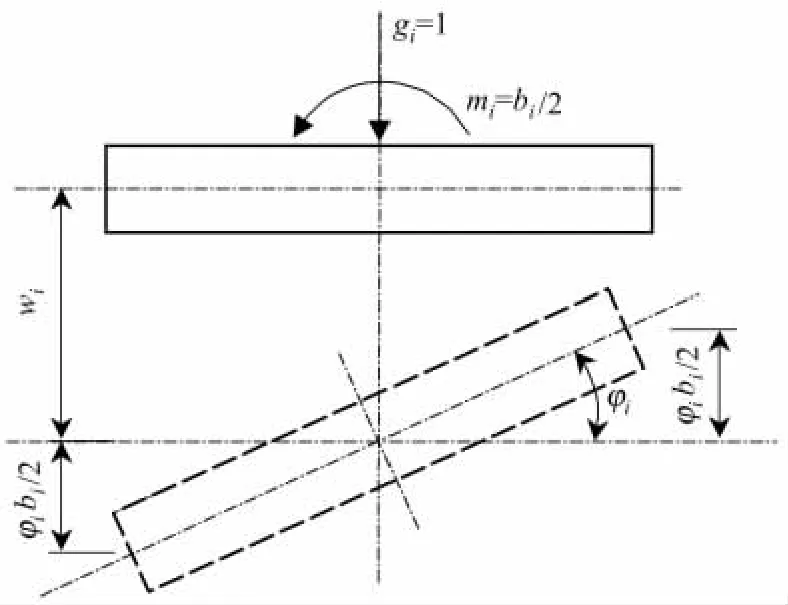
圖2 單塊板梁中力與位移的關系Fig.2 Relationship of force and displacement of slab

式中:wi為板中心單位豎向荷載作用下的跨中撓度;φi為bi/2扭矩作用下的扭轉角;bi為第i塊板的寬度;βi為第i塊板抗彎剛度修正系數，βi＞1表示板實際剛度比設計剛度大;αi為第 i塊板的抗扭剛度修正系數，αi＞1表示板實際剛度比設計剛度大.

wi和φi的計算可參見文獻［19］.

同理，可得單位鉸縫剪力及單位板上荷載作用下第i塊板右側的位移(因篇幅限制，從略).

1.3 求解修正系數的方程

鉸縫相對位移與鉸縫剪力成正比，與鉸縫剛度ki成反比，即存在以下關系:

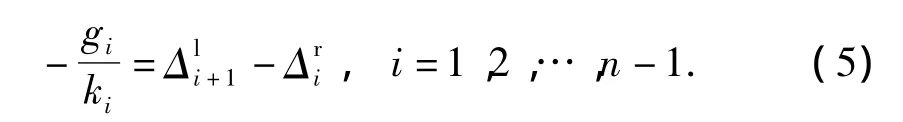
將δik和fij的表達式代入式(1)和式(2)，并考慮式(5)，整理可得關于 ki、βi及 αi的表達式.

令

式中:m 表示試驗工況，m=1，2，…，M，

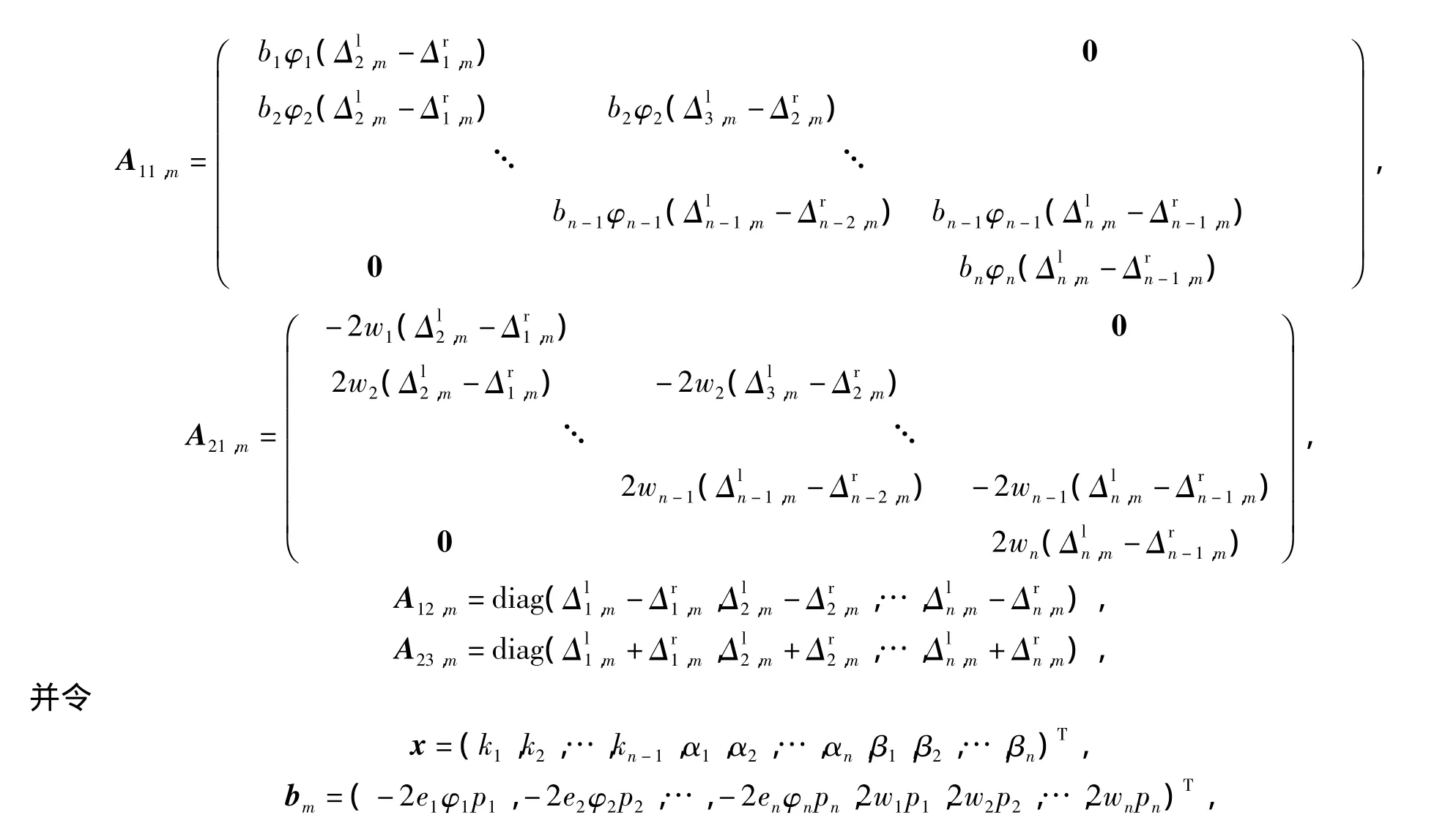
則式(1)和式(2)可寫成

方程組(6)即為1個試驗工況能列出的所有方程，共2n個.但要求解的變量一共有3n－1個，因此，需要多個試驗工況聯立求解.

1.4 模型修正

對于M個試驗工況，令

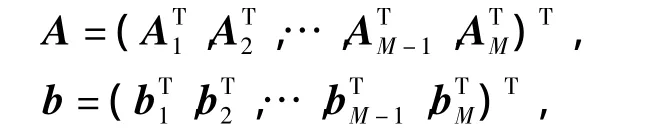
則有

方程組(7)中有2n×M個方程，需要求解的變量有3n－1個，一般來說，只要試驗工況數不少于2個，即可求得各未知參數.由于方程數多于未知變量數，無法直接求解，可采用最小二乘法，定義優化目標

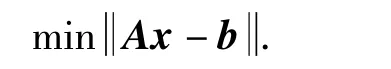
求解時對A進行QR分解，A=QR，其中Q為2nM×(3n－1)階正交矩陣，R為(3n－1)(3n－1)階上三角矩陣:

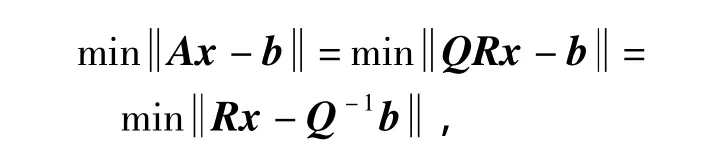
用MATLAB可很容易求得x的最優解.

2 數值模擬

若采用實橋試驗驗證提出的模型，由于無法事先了解鉸縫和板梁剛度的真實值，難以準確評價模型的正確性，這里采用數值模擬的方法驗證提出的模型.

2.1 模擬對象描述

模擬對象為單跨簡支板梁結構，計算跨徑11.0 m，橫斷面由10片空心板鉸接而成，編號自左至右依次為 1#，2#，…，10#，橫斷面見圖 3.板寬0.99 m，板高 0.55 m，相鄰板中心距為 1.00 m，混凝土強度等級為C40.板的理論參數wi=3.886×10－4m2/kN，φi=1.574×10－5m/kN.設該橋邊板實際剛度因受防撞護欄影響而增大，結合工程經驗，將抗彎剛度增大1.5倍，抗扭剛度增大1.2倍.

板梁的損傷程度按大損傷、微損傷和無損傷3種情況考慮，假設損傷主要發生在中間兩塊板，其抗彎、抗扭剛度折減系數均分別為 0.60、0.95和1.00.3種損傷情況下各板的抗彎、抗扭剛度變化系數見表1.假設鉸縫也有不同程度的損傷，其剛度從k1=6 MN/m2，按3 MN/m2等間隔增大到k9=30 MN/m2(鉸縫剪力為線分布力，單位為kN/m，因此，鉸縫剛度的單位為kN/m2).

采用汽車加載，共3個工況.每個工況均采用2輛30 t土方車，車輪布置在靠近鉸縫處，不同工況的差異是車輛位置不同.加載方式見圖3，等效荷載見表2.

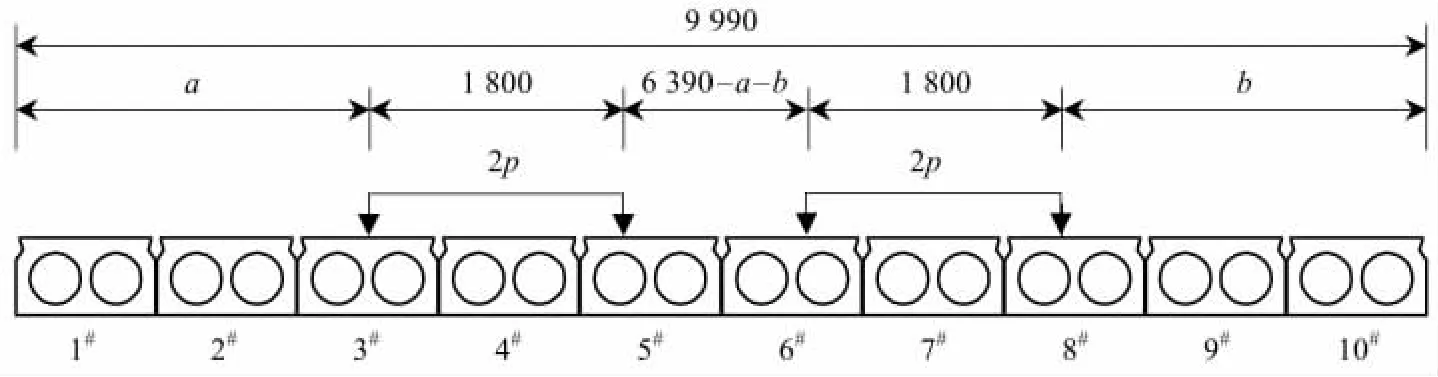
圖3 結構橫斷面及加載示意Fig.3 Section of the structure and schematic diagram of loading

表1 板梁剛度修正系數Tab.1 Correction factors of slab stiffness

荷載作用下損傷結構位移的理論值可通過式(1)和式(2)計算.考慮到實際測量精度，將計算結果按0.01 mm修約后作為實測位移值.

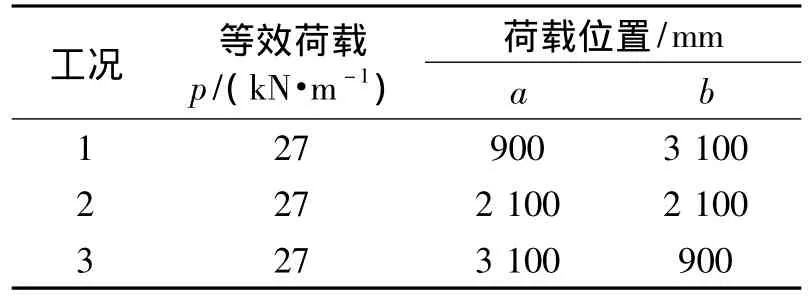
表2 等效荷載Tab.2 Equivalent load

2.2 模型修正結果及討論

2.2.1 不同工況組合下的比較

考慮表1中大損傷的情況.在不同工況組合下，將實測位移代入式(7)，可得到 ki、βi和 αi.表 3和表4為與表1中精確值相比較的誤差(“工況1+2”指在工況1和工況2下按上述方法得到的模型修正值的誤差，其余依此類推).

比較表3和表4中某2種工況和“所有工況”下計算結果的誤差，可以看出:當采用某2種工況進行分析時，計算結果在施加荷載的板和鉸縫處誤差較小，遠離荷載位置的誤差較大;當采用所有3種工況進行分析時，誤差均未超過5%.

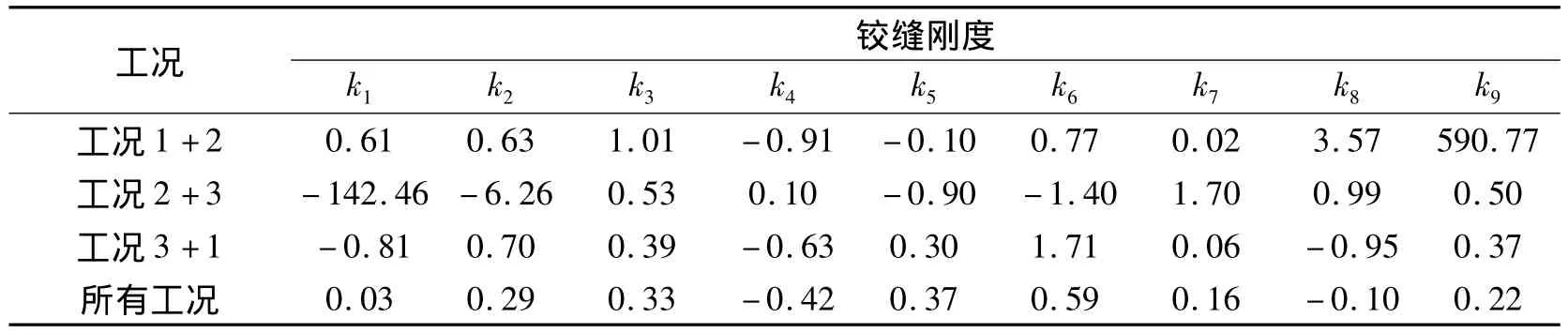
表3 不同工況下鉸縫剛度的誤差Tab.3 Error of hinge joint stiffness in different load cases %

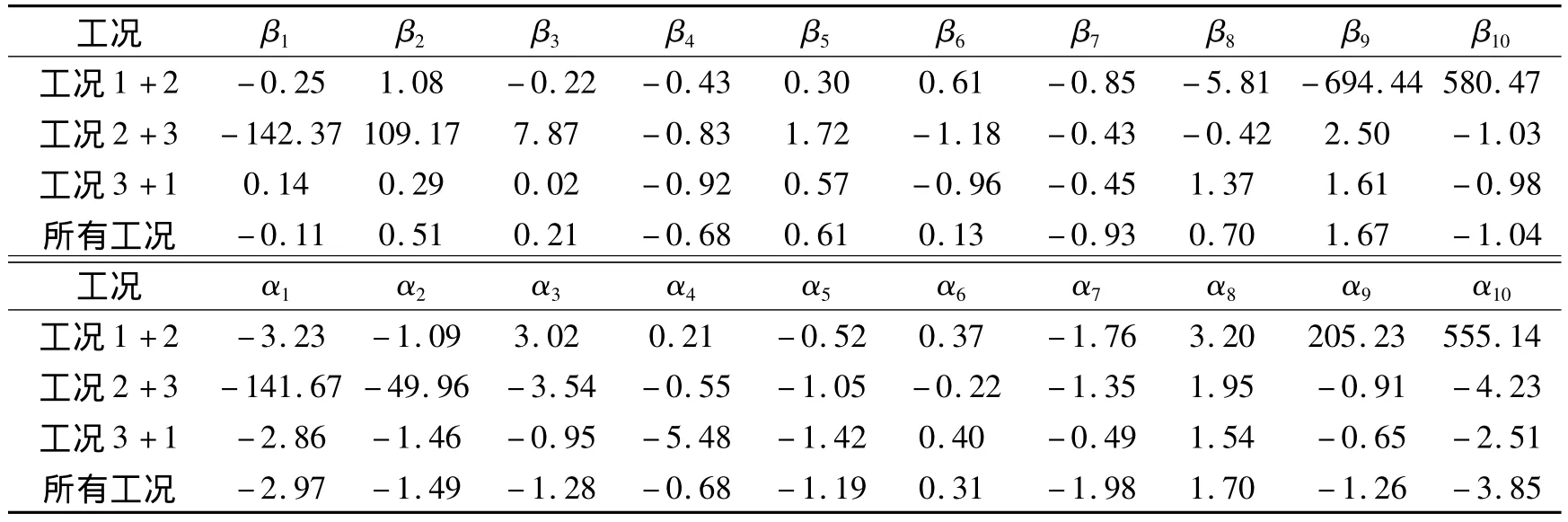
表4 不同工況下板梁剛度修正系數的誤差Tab.4 Errors of the correction factors of slab stiffness in different load cases %

造成不同工況組合分析精度不同的原因，主要是由于在不同工況下荷載位置不同造成的.當荷載位置使得鉸縫剪力、板梁彎矩和扭矩可以取得較大值時，各板邊位移就會大些.這樣，反算時所用原始數據的相對誤差將小些.因此建議，荷載試驗時，應盡可能將荷載布置在所關心的鉸縫和板上，或將多個工況組合對結構進行模型修正，以最大限度地提高測試精度、減小識別誤差.

2.2.2 與文獻［18］方法的比較

為敘述方便，稱本文方法為方法A，文獻［18］的方法為方法B.為比較2種方法的適用性，分別對大損傷、微損傷和無損傷3種情況的模型修正結果進行比較，均采用表2中所有3個工況的數據分析.針對3種損傷情況，分別采用方法A和方法B反推3種情況下板的修正系數和鉸縫剛度.對于鉸縫剛度，2種方法均能獲得，見表5;對于板的修正系數，只有用方法A才能獲得，見表6.

表5中，對于每種損傷情況均列出了3組計算結果.第1組和第2組分別為方法A和方法B獲得的鉸縫剛度的誤差(由于防撞護欄對邊板剛度的影響難以估計，計算時未考慮防撞護欄的影響);第3組為方法B獲得的鉸縫剛度的誤差(假設防撞護欄對邊板剛度的影響可以準確估計，計算時考慮了邊板剛度的增大系數(表1)).

從表5可見，無論何種損傷程度，方法A的誤差均較小.在無需了解板實際剛度和損傷程度的情況下，用方法A反演鉸縫和板的實際剛度，所得結果的誤差均較小，說明其具有普適性.反觀方法B，當采用不考慮防撞護欄影響的理論剛度時，無論板的實際損傷程度如何，均未能正確反演鉸縫的實際剛度，即使板完好、沒有損傷，計算誤差也較大.當邊板剛度可以準確估計時，對于板梁大損傷的情況，方法B得到的鉸縫剛度的誤差仍然較大;而在板梁微損傷時，方法B則可以得到較理想的效果;在無損傷時，所得結果甚至優于方法A.

以上結果說明，方法A對板梁沒有特別限制，包括有防撞護欄、隔離墩和橋面鋪裝等附屬結構造成剛度增大，或因各種損傷而造成剛度降低的情況，方法A反演結果的誤差均較小.而方法B對板梁剛度的估計要求較高，當無法準確估計板梁剛度時誤差較大;當能夠準確估計板梁剛度時，則精度較高.所以，方法A和方法B的適用范圍不同，在各自適用范圍內精度均較高.

由于方法B無法識別板的損傷，表6中只給出了方法A得到的板梁修正系數的誤差.與表5相同，無論在大損傷、微損傷還是無損傷的情況下，方法A修正結果的誤差均較小.對于邊板或次邊板發生損傷的情況也進行了分析，結果方法A相比方法B同樣具有優勢.

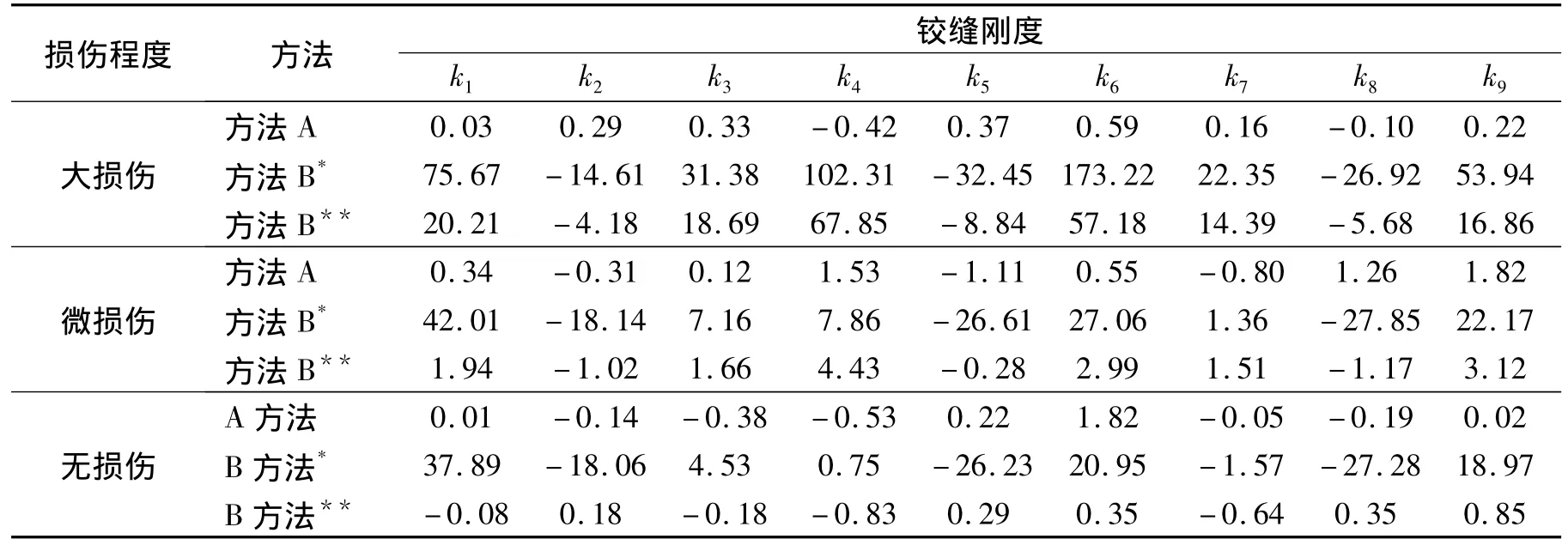
表5 不同損傷程度下鉸縫剛度的誤差Tab.5 Error of hinge joint stiffness vs.damage degree %

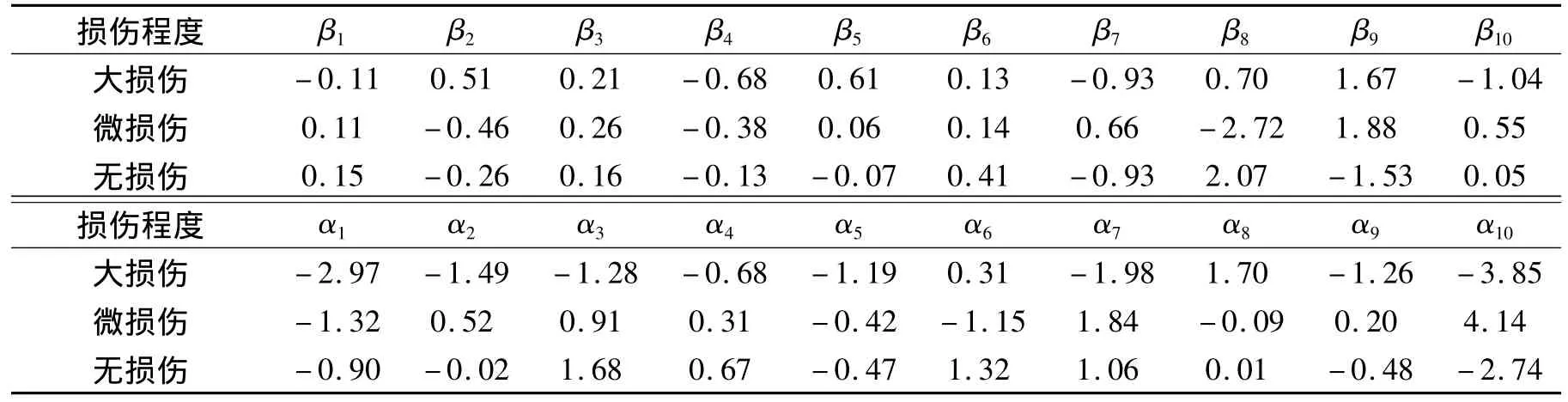
表6 不同損傷程度下板梁剛度修正系數的誤差Tab.6 Errors of the correction factors of slab stiffness vs.damage degree %

當所有位移值均為精確值而非修約值時，方法A模型修正結果的誤差為0;方法B對無損傷板(設邊板實際剛度已知)模型修正結果的誤差也為0，說明2個模型在各自的適用范圍內均可靠.

3 結論

將鉸縫剛度、板梁抗彎剛度和抗扭剛度均作為未知量，可避免板剛度無法準確估計的困難.通過引入鉸縫剛度的概念，實現了對板梁橋的模型修正.采用實測板邊位移，并用QR分解求解矛盾方程組，可直接得到參數的最優估計值.

數值模擬結果表明，無論是損傷結構，還是有復雜附屬部件的結構，提出的修正模型均能給出可靠的結果.為得到準確的參數估計值，試驗時應盡可能采用多個試驗工況，并將荷載布置在被測試的鉸縫或板附近.

［1］李義強，張彥兵，王新敏.基于參數識別的鋼筋混凝土簡支梁橋靜力模型修正技術［J］.石家莊鐵道學院學報，2006，19(3):48-51，59.LI Yiqiang，ZHANG Yanbing，WANG Xinmin.The static model updating technique based on parameter identification of reinforced concrete simply supported beam bridge［J］. JournalofShijiazhuang Railway Institute，2006，19(3):48-51，59.

［2］張啟偉，袁萬城，范立礎.公路橋梁基于模型修正理論的損傷檢測［J］.華東公路，1998(1):64-67.

［3］李海生，唐軍，葉見曙，等.混凝土梁基于靜力測試的有限元模型修正［J］.蘇州科技學院學報:工程技術版，2008，21(2):10-14.LI Haisheng，TANG Jun，YE Jianshu，et al.Updating of concrete beams based on finite element model of static test［J］. Journal of University of Science and Technology of Suzhou:Engineering and Technology，2008，21(2):10-14.

［4］黃民水，朱宏平.基于不同殘差的橋梁結構模型修正［J］.武漢理工大學學報:交通科學與工程版，2009，33(4):703-706.HUANG Minshui，ZHU Hongping.Model updating of bridgestructures based on differentresiduals［J］.Journal of Wuhan University of Technology:Transportation Science＆ Engineering，2009，33(4):703-706.

［5］歐陽歆泓，吉伯海，張宇峰.基于結構參數分析的橋梁靜態模型修正研究［J］.公路工程，2013，38(1):90-93，102.OUYANG Xinhong，JI Bohai，ZHANG Yufeng.Studies on static modelupdatingofbridgebased on the structural parameters analysis［J］.Highway Engineering，2013，38(1):90-93，102.

［6］鄧苗毅，任偉新.基于靜力荷載試驗的連續箱梁橋結構有限元模型修正［J］.福州大學學報:自然科學版，2009，37(2):261-266.DENG Miaoyi， REN Weixin. Continuous box-girder bridge structure finite element model updating based on static-load testing［J］.Journal of Fuzhou University:Natural Science Edition，2009，37(2):261-266.

［7］王元清，姚南，張天申，等.基于最優化理論的多階段模型修正及其在橋梁安全評估中的應用［J］.工程力學，2010，27(1):91-97，115.WANG Yuanqing，YAO Nan，ZHANG Tianshen，et al.An application of multistage model updating based on optimization theory to the safety appraisal of bridge［J］.Engineering Mechanics，2010，27(1):91-97，115.

［8］淳慶，邱洪興.鋼桁梁橋基于模型修正方法的損傷程度識別研究［J］.地震工程與工程振動，2005，25(2):114-118.CHUN Qing， QIU Hongxing. Research on damage degree identification of steel truss bridge based on model updating［J］.Earthquake Engineering and Engineering Vibration，2005，25(2):114-118.

［9］謝瑞杰，任偉新.基于靜動載測試的既有混凝土拱橋有限元模型修正［J］.四川建筑，2011，31(1):104-106，109.

［10］何旭輝，李鵬.既有鋼管混凝土拱橋的有限元模型修正［J］.城市道橋與防洪，2009(1):20-23.HE Xuhui，LI Peng.Finite element model updating of existing steel pipe concrete arch bridge［J］. Urban Roads Bridges＆ Flood Control，2009(1):20-23.

［11］方志，唐盛華，張國剛，等.基于多狀態下靜動態測試數據的斜拉橋模型修正［J］.中國公路學報，2011，24(1):34-41.FANG Zhi，TANG Shenghua，ZHANG Guogang，et al.Cable-stayed bridge model updating based on static and dynamic test date of multi-state［J］.China Journal of Highway and Transport，2011，24(1):34-41.

［12］熊駟東，張開銀，吳惠君.基于結構有限元模型修正的混凝土橋梁技術狀態評估［J］.中外公路，2013，33(1):186-189.

［13］楊小森，閆維明，陳彥江，等.基于模型修正的大跨斜拉橋損傷識別方法［J］.振動、測試與診斷，2012，32(2):276-281.YANG Xiaosen，YAN Weiming，CHEN Yanjiang，et al.Damage detection method for long span cablestayed bridge based on model updating［J］.Journal of Vibration，Measurement＆ Diagnosis，2012，32(2):276-281.

［14］袁愛民，戴航，孫大松.考慮邊界條件約束和參數靈敏度的斜拉橋有限元模型修正［J］.應用基礎與工程科學學報，2010，18(6):900-909.YUAN Aimin， DAIHang， SUN Dasong. Finite element model updating for a cable-stayed bridge considering the boundary condition constraintand parameter sensitivity［J］.Journal of Basic Science and Engineering，2010，18(6):900-909.

［15］夏品奇，BROWNJOHN J M W.斜拉橋有限元建模與模型修正［J］.振動工程學報，2003，16(2):219-223.XIA Pinqi，BROWNJOHN J M W.Finite element modeling and modelupdating ofa cable-stayed bridge［J］.Journal of Vibration Engineering，2003，16(2):219-223.

［16］李金寶，王達，劉揚.基于參數分析的子結構有限元模型修正技術［J］.中外公路，2012，32(3):227-233.

［17］朱張峰，郭正興.基于應變殘差的裝配式簡支梁橋有限元模型修正［J］.世界橋梁，2011(3):41-44.ZHU Zhangfeng，GUO Zhengxing.Technique of finite element model updating for fabricated simply-supported beam bridge based on strain residual［J］. World Bridges，2011(3):41-44.

［18］周正茂，袁桂芳，田清勇.基于鉸縫剛度的板梁橋鉸縫損傷評價方法［J］.中國公路學報，2013，26(5):121-130.ZHOU Zhengmao，YUAN Guifang，TIAN Qingyong.Evaluation method for hinge joint damage in multi-slab girder bridge based on the stiffness of hinge joint［J］.China Journal ofHighwayand Transport， 2013，26(5):121-130.

［19］姚玲森.橋梁工程［M］.2版.北京:人民交通出版社，2008:128-134.

［20］衛軍，李沛，張國法，等.空心板鉸縫結構耐用性能的試驗研究［J］.華中科技大學學報:自然科學版，2012，40(1):72-76.WEI Jun，LI Pei，ZHANG Guofa，et al.Experimental study on durability performance of hollow slab hinged joints［J］.Journal of Huazhong University of Science andTechnology:NaturalScienceEdition， 2012，40(1):72-76.