《幾何畫板》在圓錐曲線教學中的應用
劉書林

【摘 要】 職中生的抽象思維能力和空間思維能力是比較薄弱的,在學習平面幾何時,圖形想象能力需要建立在大量的圖形認知經驗的積累上,如果單靠手工作圖是比較耗時的。利用幾何畫板可以快速、準確且動態(tài)地向學生展示幾何圖形,幫助學生理解概念和題意,從而收到較好的教學效果。
【關鍵詞】數形結合;直觀形象;方便快捷
在職業(yè)中學的數學課堂上,我們面臨的是在初中甚至從小學開始就逐漸跟不上教學進度的學生。不要說邏輯思維能力、空間想象能力,就連最簡單的數學運算能力都是他們所欠缺的。華羅庚說:“數缺形少直觀,形缺數難入微。”在教學過程中,學生需要更為形象直觀地認知數學規(guī)律,掌握數學知識,而傳統的粉筆加尺規(guī)工具作圖,已經難以滿足他們的要求。
當前計算機技術的發(fā)展為我們解決了這一難題——從國外引進的教育軟件《幾何畫板》以其入門容易和操作簡單的優(yōu)點及其強大的圖形和圖像功能、方便的動畫功能被國內許多數學教師看好,并已成為制作中學數學課件的主要創(chuàng)作平臺之一。在教學中引用該軟件,會使一些需要結合圖形圖像的內容學習起來更加容易。我以《圓錐曲線》這一章為例,展示一下《幾何畫板》給教學和學習帶來的便利。
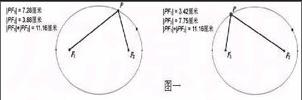
圓錐曲線中,學生首先接觸的是橢圓的第一定義:平面內,與兩定點F1、F2的距離的和等于常數(大于|F1F2|)的點的軌跡叫做橢圓。單從定義上看,學生可能想象不到這個軌跡為什么會是一個橢圓呢?我們可以通過制作動畫演示畫橢圓的過程,也可以通過看圖驗證得到,而后者更加方便快捷。在《幾何畫板》中,選擇“圓錐曲線A-橢圓(焦點+點)”功能,作任意橢圓一個。標注兩個焦點F1、F2,在橢圓上任選一點P,度量點P到點F1、F2的距離,并求和。當拖動點P在橢圓上運動時,發(fā)現|PF1|+|PF2|是一個常數(后面的學習中還會知道這個常數是2a),并不隨點P的運動而變動,如圖一。通過觀察這個圖像,學生很快理解了橢圓的定義,并能夠牢固地記住橢圓的這個特點。
(注:圖一是點P運動到橢圓上兩個不同位置時度量該點到兩焦點的距離,并求和。)
相同的方法,學生可以理解雙曲線和拋物線的第一定義,并在理解的基礎上準確記憶定義,在解決和圓錐曲線第一定義有關的題目時,答題正確率有明顯提高。如:
1.一動點到兩定點A(0,4)、B(0,-4)的距離之和為10,則它的軌跡方程為 ? ? ?。
2. 橢圓=1上一點P到一個焦點的距離為11,則P到另一個焦點的距離為 ? ? 。
3.已知F1、F2是橢圓=1的兩個焦點,過F2的直線與橢圓交于M、N兩點,求△MNF1的周長。
4.雙曲線1上任一點P到此雙曲線距離較近的一個焦點的距離是12, 則點P到另一個焦點的距離是 ? 。
5.拋物線y2=6x上一點A到焦點的距離為3,求點A到準線的距離,并求點A的橫坐標。
以上題目都是對圓錐曲線第一定義直接或者間接的考察。在講解時,可以通過幾何畫板作圖讓學生觀察。有了大量的圖形觀察經驗積累之后,學生能夠把圓錐曲線的定義轉化為動態(tài)的圖形存儲在大腦中,遇到相關題目時,可以在腦海中構建出圖形,或者很快畫出草圖,并正確解答出來。
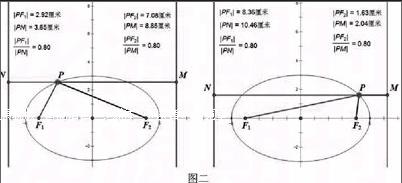
除了第一定義外,圓錐曲線的第二定義也是比較抽象,難以理解的。如橢圓的第二定義:平面內,與一個定點F的距離和到一條定直線l的距離的比是常數e(0<e<1)的點的軌跡叫做橢圓。定點F叫做橢圓的一個焦點,定直線l叫做與該焦點對應的準線(一個橢圓有兩個焦點和兩條準線)。常數e叫做橢圓的離心率。學生讀完定義后感覺不知所云,不明白為什么這樣的軌跡就是一個橢圓。我們一樣可以通過圖形驗證理解定義。作橢圓=1(如圖二),標出焦點F1、F2,并作兩條準線。在橢圓上選一動點P,當點P在橢圓上運動時,點P到左焦點的距離|PF1|和到左準線的距離|PN|是變動的,但二者的比值是不變的,而且恰好等于該橢圓的離心率e,即0.8。點P到右焦點F2的距離|PF2|和到右準線的距離|PN|也滿足這個特點。
(注:圖二是點P在橢圓上兩個不同位置時度量該點到兩焦點和兩準線的距離,并計算到焦點和到相應準線距離的比值。)
幾何畫板的演示讓第二定義變得不那么抽象,容易理解了。在遇到和第二定義相關的題目時,學生可以通過回憶圖像和定義解答問題。如:
當然,有的題目把圓錐曲線的第一、第二定義結合起來考察,那么觀察圖形的經驗積累就顯得更加重要了。如:1(上一點P到左焦點距離是12,它到橢圓右準線的距離是 ? ?。
從近幾年的教學經驗來看,在講解圓錐曲線時,使用幾何畫板會使得三種圓錐曲線的定義講解得更加清晰,學生接受起來也更加輕松,不容易遺忘,解答題目時會想到用這些相應的知識。由此可見,課堂中引入幾何畫板,會使本來抽象不容易理解的概念、需要圖形想象能力的知識接受起來更加容易。當然學習中不需要每次都用幾何畫板,這樣又顯得有些繁瑣,主要是在學習一個新知識點的初期運用幾何畫板幫助學生理解概念,建立直觀形象的圖形印象,這會使得后面的學習變得輕松很多。
當然,這里只是使用了《幾何畫板》中一些最基本、最簡單的功能,這也只是我初步嘗試在課堂使用該軟件的小小收獲,愿意和大家一起分享。
(作者單位:東莞市商業(yè)學校)

