基于數據插值的二維MUSIC譜峰搜索算法
馬英英 劉帥 金銘


摘 要: 針對MUSIC算法在進行二維到達角估計時運算量大、估計速度較慢的問題,對基于數據插值二維MUSIC譜峰搜索算法進行研究。在MUSIC算法的基礎上先用較大步長在二維空間進行粗略搜索,之后在粗搜譜峰位置附近的小區間內進行二維插值,最后用小步長在該區間內進行譜峰搜索,得到精確的角度估計值。仿真實驗表明,該算法可有效地減少二維空間搜索的運算量。
關鍵詞: MUSIC算法; 譜峰搜索; 運算量; 數據插值
中圖分類號: TN911.7?34 文獻標識碼: A 文章編號: 1004?373X(2015)15?0035?04
Two?dimensional MUSIC spectrum?peak searching algorithm based on data interpolation
MA Yingying, LIU Shuai, JIN Ming
(School of Information and Electrical Engineering, Harbin Institute of Technology (Weihai Branch), Weihai 264209, China)
Abstract: Since multiple signals classification (MUSIC) algorithm has large calculation quantity and low estimation speed when estimating two?dimensional angle of arrival (AOA), two?dimensional MUSIC spectrum?peak searching algorithm based on data interpolation is studied. On the basis of MUSIC algorithm, larger step is applied to proceed rough searching in two?dimensional space, then two?dimensional interpolation is conducted in minizone near searched spectrum?peak position. Spectrum?peak searching is carried on in the zone with smaller step, and precise angle estimation value is obtained. Simulation experiments indicate that the algorithm can reduce calculation quantity in two?dimensional space searching effectively.
Keywords: MUSIC algorithm; spectrum?peak searching; calculation quantity; data interpolation
0 引 言
空間譜估計測向技術[1]作為一門新興的空間信號處理技術,在雷達、聲納、氣象、通信等相關領域中都有著廣泛應用[2] 。多重信號分類[3](Multiple Signal Classification,MUSIC)算法作為一種高分辨率的譜估計方法使得空間譜估計技術進入了超分辨測角階段。經典MUSIC算法因為需要進行協方差矩陣的計算、特征值分解和譜峰搜索,計算量很大,特別是在二維或多維空間進行搜索時,計算量尤其大,很難在工程中應用。后來人們在其基礎上提出了很多改進算法。其中,1985年Roy和Kailath提出的借助旋轉不變技術的參數估計算法[4](Estimating Signal Parameters Via Rotational Invariance Techniques,ESPRIT)是利用陣列流形的某些特性形成一個可以直接求解的函數,能夠比較方便地得到所需要的估計參數;Barabell提出的求根MUSIC算法[5]根據多項式求根進行參數估計。但上述兩種算法對陣列形式均有要求,求根MUSIC算法僅能用于一維陣列且ESPRIT算法在二維條件下存在參數配對問題。而另一部分改進算法還是不能避免譜峰搜索[6?8],如基于空間平滑技術去相關的MUSIC(MMUSIC)算法[9],在譜峰搜索上的運算量還是很大。因此有學者提出,可以結合數值方法中的插值法進行譜峰搜索,可有效地減少運算量。
數據插值方法[10]是數值分析中的最基本方法之一,主要解決的問題是根據離散數據構造一個簡單易于計算的函數代替原有的復雜函數。本文將插值算法應用在譜峰搜索當中,可以大大減少搜索的點數,從而減少計算量,并且對陣列形式無特殊要求。
1 MUSIC算法二維空間譜估計
用如圖1所示的均勻平面陣來估計二維空間譜的方位角與俯仰角。
設陣元位置為[(xk,yk), k=1,2,…,M,]信號入射參數為[(θi,φi), i=1,2,…,N,]分別表示方位角與俯仰角,其中方位角表示與[x]軸的夾角。
以原點處為參考陣元,則各陣元相對參考陣元的時延為:
[τki=1c(xkcosθicosφi+yksinθicosφi)] (1)
圖1 均勻平面陣
對于遠場窄帶信號,整個天線陣列所接收到的信號為:
[X(t)=AS(t)+N(t)] (2)
式中:[X(t)]為陣列的[M×1]維快拍數據矢量;[N(t)]為陣列的[M×1]維噪聲數據矢量;[S(t)]為空間信號的[N×1]維矢量;[A]為空間陣列的[M×N]維流型導向矢量陣,且:
[A=[a1(φ,θ) a2(φ,θ) … aN(φ,θ)]] (3)
其中,導向矢量:
[ai(φ,θ)=ej2πλ(x1sinθicosφi+y1sinθisinφi),…,ej2πλ(xNsinθicosφi+yNsinθisinφi)T] (4)
式中[λ]為波長。
得到陣列的接收信號模型后進行二維空間譜估計。首先求陣列輸出的相關矩陣[R∈CN×N],有:
[R=1Li=1LXXH] (5)
對[R]進行特征分解,則其[N-K]個較小特征值對應的特征向量張成了[R]的噪聲子空間[UN]。利用噪聲子空間與信號方向矢量正交即[UN⊥span{A}]的特性,得空間二維MUSIC算法定義的空間譜函數為:
[PMUSIC=1aH(φ,θ)UNUHNa(φ,θ)] (6)
對空間譜函數進行二維搜索,獲得的譜峰處即指示信號來波方向的[(φk,θk)]。
2 插值算法
數學上常用的插值法[11]有Lagrange插值,Newton插值,Hermite插值等多項式插值法以及分段低次插值法,分段三次樣條插值等分段插值法。多項式插值法在插值多項式次數較高時會出現不收斂的龍格現象;分段低次多項式插值通常計算簡單但曲線光滑性差;分段三次多項式插值要求插值函數具有連續的二階導數,可以得到具有更高光滑度的曲線。鑒于MUSIC譜圖的譜峰非常尖銳,所以為得到更高的精度本文選用分段三次樣條插值法,并與分段線性插值法,分段三次多項式插值法作比較。
2.1 分段線性插值
對給定區間[[a,b]]做劃分[Δ:a=x0 (1) [φ(x)]在區間[[a,b]]上連續; (2) [φ(xi)=yi,i=0,1,2,…,n]; (3) [φ(x)]在每個子區間[[xi,xi+1]]上是線性函數。 則稱[φ(x)]為[[a,b]]上關于數據[(xi,yi),i=0,1,2,…,n]的分段線性插值函數。 同理,若[φ(x)]在每個子區間[[xi,xi+1]]上是三次多項式,則稱[φ(x)]為[[a,b]]上關于數據[(xi,yi),i=0,1,2,…,n]的分段三次多項式插值函數。 2.2 分段三次樣條插值 對給定區間[[a,b]]做劃分[Δ:a=x0 (1)[S(x)]在[[a,b]]上具有連續的二階導數; (2)[S(xi)=yi,i=0,1,2,…,n]; (3)[S(x)]在每個子段[[xi,xi+1]]上都是三次多項式。 則稱[S(x)]為分段三次樣條函數。 當[x∈[xi,xi+1]]時,記[hi=xi+1-xi,][S(x)]的一般表達式為: [S(x)=Mi(xi+1-x)6h3+Mi+1(x-xi)36h+yi-Mih26 xi+1-xh+yi+1-Mi+1h26 x-xih] (7) 式中:[Mi,i=0,1,2,…,n]是需要待定的系數,且[Mi=][S(xi)]。 據[S(xi+0)=S(xi-0)],可得[n-1]個條件: [μiMi-1+2Mi+λiMi+1=di,i=1,2,…,n-1] (8) [式中:][λi=hi+1hi+hi+1,][μi=hihi+hi+1=1-λi,][di=6hi+hi+1?] [yi+1-yihi+1-yi-yi-1hi=][6f(xi-1,xi,xi+1)]。。。 由于[n+1]個數據點需要[n+1]個系數,而式(8)只提供了[n-1]個條件,所以通過端點約束,即增加邊界條件來補充另外兩個條件。邊界條件一共有三種,分別是: (1) 第一種邊界條件 [S(x0)=f(x0),S(xn)=f(xn)] (9) (2) 第二種邊界條件 [S(x0)=f(x0),S(xn)=f(xn)] (10) 若[S(x0)=S(xn)=0,]則稱之為自然邊界,滿足自然邊界的樣條函數稱為自然樣條,它是通過所有數據點的插值函數中總曲率最小的惟一函數,因此自然三次樣條是插值所有數據點的最光滑函數。 (3) 第三種邊界條件 當被插值函數是以[b-a]為周期的周期函數時,則要求[S(x)]也是周期函數,這時,邊界條件為: [S(x0+0)=S(xn-0),S(x0+0)=S(xn-0),S(x0+0)=S(xn-0)] (11) 這樣就可以解出[n+1]個系數了,再將其代入到式(7)就可以得到相應子區間內的樣條函數。 在利用上述插值方法對MUSIC算法粗搜的二維空間譜進行插值時,先利用得到的數據在[x]軸方向進行插值,再用同樣的插值法對[y]軸方向進行插值,這樣就得到了經二維插值后的MUSIC空間譜圖。 3 仿真及分析 實驗中采用8陣元[L]陣,信號入射角為(30.45°,60.27°),在高斯白噪聲條件下進行。信噪比為30 dB,快拍數為1 024。性能分析實驗中蒙特卡洛次數為100次。仿真結果的插值區域均為以粗搜譜峰為中心,邊長為2°的正方形區域。
3.1 基于插值的譜峰搜索算法實現
圖2為搜索步長為0.1°時,MUSIC算法在二維空間中搜索的譜圖;圖3為在MUSIC算法0.1°搜索的基礎上,用分段線性插值法進行插值后的譜圖;圖4為在MUSIC算法0.1°搜索的基礎上,用分段三次多項式插值法進行插值后的譜圖;圖5為在MUSIC算法0.1°搜索的基礎上,用分段三次樣條插值法進行插值后的譜圖。可以看出經插值后的譜圖要比圖2密集得多,理論上譜峰搜索的精度也會提高,下面通過仿真來比較幾種算法的性能。
圖2 二維MUSIC算法0.1°粗搜譜圖
圖3 分段線性插值譜圖
3.2 性能比較
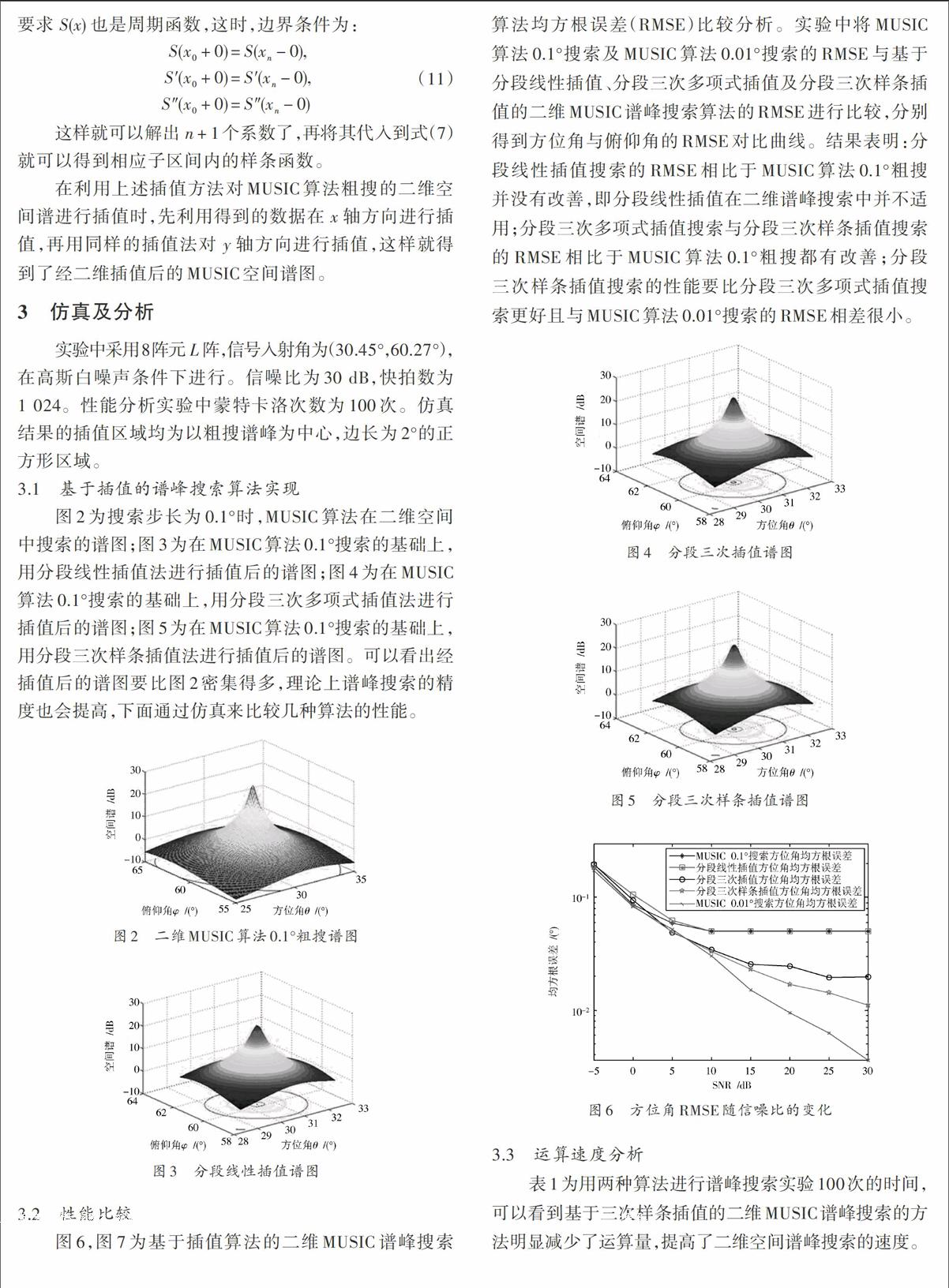
圖6,圖7為基于插值算法的二維MUSIC譜峰搜索算法均方根誤差(RMSE)比較分析。實驗中將MUSIC算法0.1°搜索及MUSIC算法0.01°搜索的RMSE與基于分段線性插值、分段三次多項式插值及分段三次樣條插值的二維MUSIC譜峰搜索算法的RMSE進行比較,分別得到方位角與俯仰角的RMSE對比曲線。結果表明:分段線性插值搜索的RMSE相比于MUSIC算法0.1°粗搜并沒有改善,即分段線性插值在二維譜峰搜索中并不適用;分段三次多項式插值搜索與分段三次樣條插值搜索的RMSE相比于MUSIC算法0.1°粗搜都有改善;分段三次樣條插值搜索的性能要比分段三次多項式插值搜索更好且與MUSIC算法0.01°搜索的RMSE相差很小。
圖4 分段三次插值譜圖
圖5 分段三次樣條插值譜圖
圖6 方位角RMSE隨信噪比的變化
3.3 運算速度分析
表1為用兩種算法進行譜峰搜索實驗100次的時間,可以看到基于三次樣條插值的二維MUSIC譜峰搜索的方法明顯減少了運算量,提高了二維空間譜峰搜索的速度。
圖7 俯仰角RMSE隨信噪比的變化
表1 算法耗時比較
[算法\&MUSIC算法0.01°搜索\&分段三次樣條插值\&耗時 /s\&151.755\&41.536\&]
4 結 論
MUSIC算法作為一種高分辨率的譜估計方法使得空間譜估計技術進入了超分辨測角階段,但譜峰搜索的過程運算量很大,尤其是在二維空間中。所以如何快速準確地進行譜峰搜索是當前需要解決的重要問題之一,本文主要研究了基于多種插值算法的MUSIC譜峰搜索算法。
在二維空間中建立了平面[L]陣的陣列信號模型,仿真得到了二維插值搜索的空間譜圖,通過對算法性能在參數影響和運算速度兩個方面的對比分析,得到如下結論:
(1) 基于分段線性插值的二維MUSIC譜峰搜索算法的RMSE相比于MUSIC算法0.1°粗搜并沒有提高,所以分段線性插值法在二維MUSIC譜峰搜索中不適用。
(2) 基于分段三次多項式插值及分段三次樣條插值的二維MUSIC譜峰搜索的RMSE相比于MUSIC算法0.1°粗搜都有改善;分段三次樣條插值搜索的性能要比分段三次多項式插值搜索更好且與MUSIC算法0.01°搜索的RMSE相差很小。
(3) 基于分段三次樣條插值的二維MUSIC譜峰搜索算法相比MUSIC算法0.01°搜索明顯減少了運算量,大大提高了二維空間譜峰搜索的速度。
參考文獻
[1] 王永良,陳輝,彭應寧,等.空間譜估計理論與算法[M].北京:清華大學出版社,2007.
[2] KRIM H, VIBERG M. Two decades of array signal processing research [J]. IEEE Signal Processing Magazine, 1996, 13(4): 67?69.
[3] SCHMIDT R O. Multiple emitter location and signal parameter estimation [J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276?280.
[4] GAO F, GERSHMAN A B. A generalized ESPRIT approach to direction?of?arrival estimation [J]. Signal Processing Letters, 2005, 12(3): 254?257.
[5] RAOB D, HARI K V S. Performance analysis of root?music. IEEE Transactions Acoustics, Speech and Signal Processing, 1989, 37(12): 1939?1949.
[6] 吳世龍,羅景青,劉有軍.一種用于二維MUSIC算法的譜峰識別方法研究[J].信號處理,2005,21(z1):16?19.
[7] 吳江華,周圍.DOA估計的一種改進MUSIC算法[J].無線電通信技術,2008,34(1):39?42.
[8] 周小軍,譚薇,馮大政,等.基于解相干的改進MUSIC算法DOA估計[J].無線電工程,2014,44(12):18?21.
[9] 何子述,黃振興.修正MUSIC算法對相關信號源的DOA估計性能[J].通信學報,2000,21(10):14?17.
[10] MATHEWS J H,FINK K D.數值方法(Matlab版)[M].北京:電子工業出版社,2010.
[11] 張麗娟.三種插值方法的應用與比較[J].赤峰學院學報:自然科學版,2010,26(3):1?3.

