一類改進Boussinesq方程的Lie對稱群及群不變解

張 錦,王鄉月

(吉林大學 數學學院,長春 130012)

?

一類改進Boussinesq方程的Lie對稱群及群不變解

張 錦,王鄉月

(吉林大學 數學學院,長春 130012)

利用經典Lie群方法研究一類改進Boussinesq方程的Lie對稱群的存在性及相應的群不變解,證明了改進Boussinesq方程存在3-參數的Lie對稱群,并得到了該方程的一些行波解和非行波解.

Lie群;Lie對稱;Boussinesq方程;群不變解

Boussinesq方程[1]的一般形式為

utt=uxx+quxxxx+(u2)xx,q=±1,

它不僅與水波傳播密切相關,而且還可用于模擬其他波動現象,如物理學中的聲波、離子波及醫學中血管內的孤波等.但Boussinesq方程用于描述短波的傳播時具有不穩定性,因此Bogolubsky[2]又提出了如下改進Boussinesq方程:

utt=uxx+quttxx+(u2)xx,q=±1.

改進Boussinesq方程可以很好地模擬圓截面彈性桿中聲波的橫向運動和非線性運動.

目前,對于非線性微分方程的求解有很多可行方法,Lie群方法[3]是其中之一.利用Lie群方法對Boussinesq方程進行研究已取得豐富的結果[4-11].本文通過對改進Boussinesq方程進行Lie對稱分析,得到了該方程的Lie對稱群以及相應的群不變解.

考慮如下改進Boussinesq方程:

(1)

其中q是任意常數.利用經典的Lie群方法可以得到如下結果.

定理1改進Boussinesq方程(1)存在3-參數的Lie對稱群.

證明:考慮如下單參數Lie變換群:

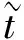
(2)

其中:ε?1是小參數;τ(t,x,u),ξ(t,x,u),φ(t,x,u)是關于t,x,u的光滑函數.Lie變換群(2)的無窮小生成元為

V=τ(t,x,u)?t+ξ(t,x,u)?x+φ(t,x,u)?u,

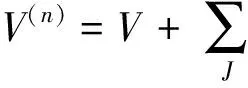
對方程(1)的所有解都成立.等價于求解方程

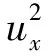
(3)

其中Q=Q(t,x,u(4))是依賴于t,x,u及u關于t,x的直到4階導數的光滑函數,并且

將各φJ的表達式代入方程(3),并比較u的各階導數系數,可得如下確定性方程組:

τx=0,τu=0,τtt=0,ξt=0,ξx=0,ξu=0,φx=0,φtt=0,φuu=0,φ=-(1+2u)τt.

求解該方程組得

τ=a+ct,ξ=b,φ=-c-2cu,

其中a,b,c是任意常數.表明方程(1)的Lie對稱群的生成元構成一個三維的Lie對稱代數,并有如下一組基:

V1=?t,V2=?x,V3=t?t-(1+2u)?u.

證畢.

利用定理1,可得如下關于改進Boussinesq方程的單參數群不變解的結果.

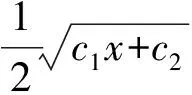
2)對應于Lie對稱V2的群不變解為u=c1t+c2;

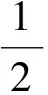
式中c1和c2都是任意常數.

(4)

這里 ′=d/dx.在方程(4)兩端同時乘以2(6q+f)f′并積分可得

(6q+f)2f′2=36qf2+4f3+c1,

其中c1是任意常數.進一步求解該方程可知結論成立.

實際上,通過考慮Lie對稱代數的線性組合,可以得到更一般的關于群不變解存在性的結果.

定理31)對應于向量場aV1+bV2(a,b≠0)的群不變解為u=f(ax-bt),這里f(y)滿足

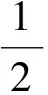
3)對應于向量場aV1+bV2+cV3(b,c≠0)的群不變解為

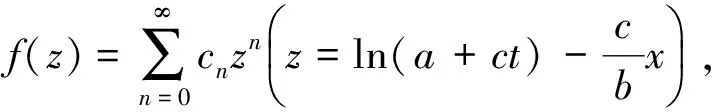
式中c0,c1,c2和c3都是任意常數.

證明:Boussinesq方程(1)的3-參數Lie對稱群為

若u=f(t,x)是方程(1)的解,則

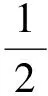
是可由群不變性得到的方程(1)的最一般解.

1)利用aV1+bV2的不變量ζ1=ax-bt和ζ2=u可知相應的群不變解為u=f(ax-bt).將其代入方程(1),可得f(y)滿足的方程為

(5)

這里 ′=d/dy.方程(5)等價于下述二階方程:

(6)

其中c0和c1是任意常數.特別地,令c0=0,并在方程(6)兩端同時乘以6f′再積分可知

(7)

其中c2是任意常數.進一步求解方程(7)可知結論成立.

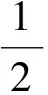
(8)

這里 ′=d/dx.在方程(8)兩端同時乘以2(6qc2+f)f′并積分可得

(9)

其中c1是任意常數.進一步求解方程(9)可知結論成立.

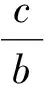
將其代入方程(1),可得f(z)滿足的方程為

(10)

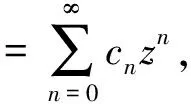
比較z的同次冪項系數即知結論成立.

綜上,本文利用Lie對稱方法求出了一類改進Boussinesq方程的Lie對稱群,并得到了該方程的一些行波解、非行波解及最一般群不變解所滿足的方程和相應的冪級數解.

[1] Boussinesq J.Théorie des Ondes et des Remous Qui se Propagent le Long D’un Canal Rectangulaire Horizontal en Communiquant au Liquide Contenu Dans ce Canal des Vitesses Sensiblement Pareilles de la Surface au Fond [J].J Math Pures Appl,1872,17(2):55-108.

[2] Bogolubsky I L.Some Examples of Inelastic Soliton Interaction [J].Comput Phys Comm,1977,13(3):149-155.

[3] Olver P J.Applications of Lie Groups to Differential Equations [M].New York:Springer-Verlag,1993.

[4] Barannik L F,Lahno H O.Symmetry Reduction of the Boussinesq Equation to Ordinary Differential Equations [J].Rep Math Phys,1996,38(1):1-9.

[5] Clarkson P A.Nonclassical Symmetry Reductions of the Boussinesq Equation [J].Chaos Solitons Fractals,1995,5(12):2261-2301.

[6] Levi D,Winternitz P.Non-classical Symmetry Reduction:Example of the Boussinesq Equation [J].J Phys A:Math Gen,1989,22(15):2915-2924.

[7] Clarkson P A,Ludlow D K.Symmetry Reductions,Exact Solutions,and Painlevé Analysis for a Generalised Boussinesq Equation [J].J Math Anal Appl,1994,186(1):132-155.

[8] Gandarias M L,Bruzón M S.Classical and Nonclassical Symmetries of a Generalized Boussinesq Equation [J].J Nonlinear Math Phys,1998,5(1):8-12.

[9] Bruzón M S,Gandarias M L.Symmetries for a Family of Boussinesq Equations with Nonlinear Dispersion [J].Commun Nonlinear Sci Numer Simul,2009,14(8):3250-3257.

[10] Moleleki L D,Khalique C M.Symmetries,Traveling Wave Solutions,and Conservation Laws of a (3+1)-Dimensional Boussinesq Equation [J].Adv Math Phys,2014,2014:672-679.

[11] 王兆燕,劉希強.(3+1)維Boussinesq方程的對稱、約化及精確解 [J].純粹數學與應用數學,2011,27(6):781-786.(WANG Zhaoyan,LIU Xiqiang.Symmetries,Reductions and Exact Solutions of (3+1)-Dimensional Boussinesq Equation [J].Pure Appl Math,2011,27(6):781-786.)

(責任編輯：趙立芹)

LieSymmetryAnalysisandGroup-InvariantSolutionsforanImprovedBoussinesqEquation

ZHANG Jin,WANG Xiangyue

(CollegeofMathematics,JilinUniversity,Changchun130012,China)

Applying the classical Lie symmetry method,we investigated the problem of determining the largest possible set of Lie point symmetries for an improved Boussinesq equation.The most general Lie point symmetry group of the improved Boussinesq equation was determined and the corresponding group-invariant solutions,such as travelling wave solutions were obtained.

Lie group;Lie symmetry;Boussinesq equation;group-invariant solution

10.13413/j.cnki.jdxblxb.2015.03.02

2014-10-21.

張 錦(1982—),女,漢族,博士,講師,從事Lie群在微分方程中應用的研究,E-mail:jinzhang@jlu.edu.cn.

國家自然科學基金(批準號:J1310022;11001102).

O175.2

：A

：1671-5489(2015)03-0359-04