擬周期平面振子平衡點的穩定性

邢秀梅,任秀芳

(1.伊犁師范學院 數學與統計學院,新疆 伊寧 835000;2.南京農業大學 理學院數學系,南京 210095)

?

擬周期平面振子平衡點的穩定性

邢秀梅1,任秀芳2

(1.伊犁師范學院 數學與統計學院,新疆 伊寧 835000;2.南京農業大學 理學院數學系,南京 210095)

利用主積分方法,將周期系統平衡點的穩定性判據推廣到擬周期情形,即證明擬周期二階微分方程x″+h(t)x′+a(t)x2n+1+e(t,x)=0(n≥1)平衡點x=x′=0的穩定性,其中h(t),a(t),e(t,x)是擬周期系數,其頻率向量滿足Diophantine條件,且在x=x′=0附近,|e(t,x)|=O(x2n+2).結果表明,具有變號阻尼項擬周期振子的平衡點在一定條件下具有穩定性.

擬周期;Diophantine條件;平衡點穩定性

0 引 言

近年來,對擬周期微分方程的研究受到人們廣泛關注.關于周期微分方程平衡點穩定性的研究已有許多結果[1-9].儲繼峰等[1]考慮具有一個半自由度的阻尼震蕩系統：

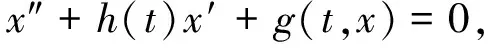
(1)

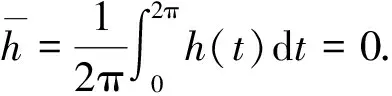
(2)

本文將劉期懷等[2]的相關結果推廣到擬周期微分方程：即在方程(2)中,要求e(t,x)在x=0附近滿足|e(t,x)|=O(x2n+2),h(t),a(t),e(t,x)關于t,x是實解析的,并且關于t是擬周期函數,相應的頻率向量(ω1,ω2,…,ωm)滿足Diophantine條件：即存在常數γ>0和τ>m-1,使得對一切k=(k1,k2,…,km)≠0,都有

(3)

其中|k|=|k1|+|k2|+…+|km|.

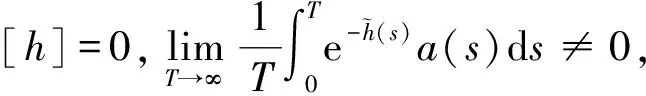
1)方程(2)的平衡點x=x′=0是穩定的;

1 典則變換

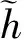
(4)

相應的Hamiltonian函數為

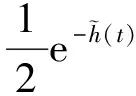
(5)

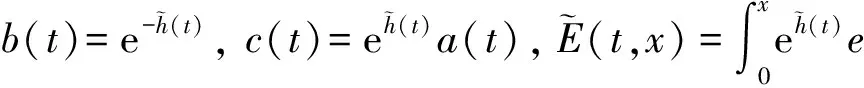
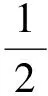
(6)

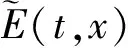
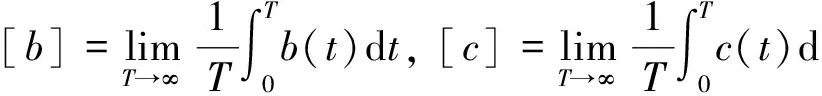
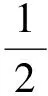
(7)

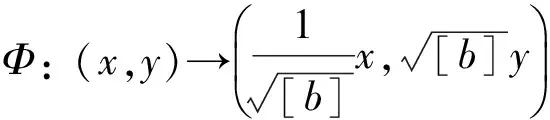
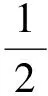
(8)

考慮輔助系統

(9)

令c=|[c]|[b]n+1.記(C(t),S(t))是方程(9)的滿足初始條件(C(0),S(0))=(1,0)的周期解.令T>0為其最小正周期,則這些函數滿足下列條件:

(10)

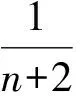
2 不穩定性的證明

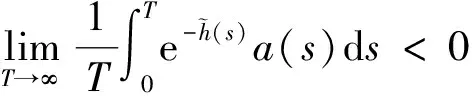
1)首先,引進典則變換:

則Hamiltonian函數(8)變為

(11)

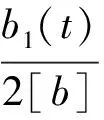
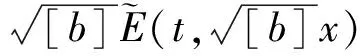
其次,定義一個與時間相關的典則變換:

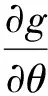
其中

(12)

它關于t是擬周期的.則變換后的Hamiltonian函數(11)具有如下形式:

其中

(13)

令

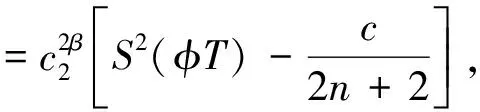
(14)

利用式(12)和2β>1,得

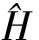
(15)

2)不穩定性的證明.考慮關于變量λ,φ的動力系統

(16)

首先,證明存在一個φ*和0<υ<1,使得ψ(φ*)=0,并且當|φ-φ*|≤υ時,下述結論成立:

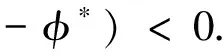
(17)

事實上,由式(10)有

并且

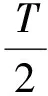
記m=min{|ψ(φ*+υ)|,|ψ(φ*-υ)|}.對于系統(16),存在常數r0>0,使得當|λ|≤r0時,下述不等式成立：

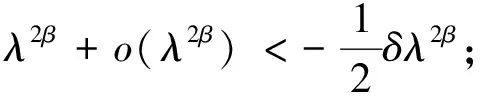
(19)

其次,定義角形區域Sε={(λ,φ)||λ|≤ε,|φ-φ*|≤υ},則必存在一點(λ0,φ0)∈Sε和某一時刻t*<0,使得λ(t*,λ0,ψ0)≥r0.

事實上,否則方程(16)的負向解屬于集合

(20)

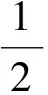
3 穩定性的證明

1)由于[c]>0,所以典則變換Φ1將Hamiltonian函數(8)變為

(21)

其中：

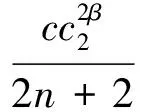
顯然f1(t,θ)關于t的均值為零、關于θ是1周期的.

2)利用典則變換Φ2,使變換后的Hamiltonian函數(21)具有如下形式:

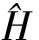
其中

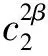
(22)

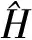
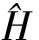
(23)

(24)

(25)

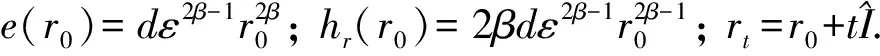
可得

(26)

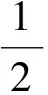
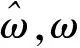
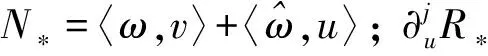
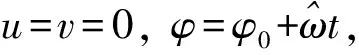
對于固定的t,解λ,φ在每一時刻t關于φ0連續,相應的積分曲線形成了t軸的管狀領域.由解的存在唯一性知,該管狀內出發的解永遠位于管狀領域內.由于該管狀領域大小由ε控制,而且ε可任意小,因此得到系統(23)的不動點λ=0是穩定的.

參考文獻

[1] CHU Jifeng,DING Jinhong,JIANG Yongxin.Lyapunov Stability of Elliptic Periodic Solutions of Nonlinear Damped Equations [J].J Math Anal Appl,2012,396(1):294-301.

[2] LIU Qihuai,QIAN Dingbian,WANG Zhiguo.The Stability of the Equilibrium of the Damped Oscillator with Damping Changing Sign [J].Nonlinear Anal:Theory,Methods &Appl,2010,73(7):2071-2077.

[3] Chetayev N G.The Stability of Motion [M].New York:Pergamon Press,1961.

[4] Dieckerhoff R,Zehnder E.Boundedness of Solutions via the Twist-Theorem [J].Ann Scuola Norm Sup Pisa Cl Sci,1987,14(1):79-95.

[5] LIU Bin.The Stability of the Equilibrium of Planar Hamiltonian and Reversible Systems [J].J Dyn Differ Equ,2006,18(4):975-990.

[6] Bibikov Yu N.On the Stability of the Zero Solution of Essentially Nonlinear Hamiltonian System and Reversible Systems with One Degree of Freedom [J].Differ Equ,2002,38(5):579-584.

[7] LIU Bin.The Stability of Equilibrium of Quasi-periodic Planar Hamiltonian and Reversible Systems [J].Science in China Series A:Mathematics,2010,53(1):125-136.

[8] LIU Bingwen.Global Exponential Stability of Positive Periodic Solutions for a Delayed Nicholson’s Blowflies Model [J].J Math Anal Appl,2014,412(1):212-221.

[9] LI Lin,LIU Zhicheng.Existence of Periodic Solutions and Stability of Zero Solution of a Mathematical Model of Schistosomiasis [J/OL].J Appl Math,2014-02-13.http://dx.doi.org/10.1155/2014/765498.

[10] WU Yunchao,WANG Yiqian.The Stability of the Elliptic Equilibrium of Planar Quasi-periodic Hamiltonian Systems [J].Acta Math Sin:Engl Ser,2012,28(4):801-816.

[11] P?schel J.A Lecture on the Classical KAM Theorem [J].Proc Sympos Pure Math,2001,69(2):707-732.

(責任編輯：趙立芹)

StabilityoftheEquilibriumofQuasi-periodicPlanarOscillator

XING Xiumei1,REN Xiufang2

(1.SchoolofMathematicsandStatistics,YiliNormalUniversity,Yining835000,XinjiangUygurAutonomousRegion,China;2.DepartmentofMathematics,CollegeofScience,NanjingAgriculturalUniversity,Nanjing210095,China)

We generalized the stability criteria for the equilibrium of the periodic system to those for that of quasi-periodic system,applying the method of main integration.Concretely,we showed the stability for the equilibriumx=x′=0 of the quasi-periodic second order differential equationx″+h(t)x′+a(t)x2n+1+e(t,x)=0,n≥1,whereh(t),a(t),e(t,x)are quasi-periodic coefficients,whose frequency vectors meet the requirements proposed by Diophantine.And moreover,|e(t,x)|=O(x2n+2)nearx=x′=0.The results we obtained also imply that,under some conditions,the equilibrium of the quasi-periodic oscillator with damping changing sign can still be stable.

quasi-periodic;Diophantine condition;stability of the equilibrium

10.13413/j.cnki.jdxblxb.2015.03.07

2014-10-27.< class="emphasis_bold">網絡出版時間

時間：2015-02-11.

邢秀梅(1973—),女,漢族,博士,講師,從事Hamiltonian系統的研究,E-mail:xingxm09@163.com.通信作者:任秀芳(1982—),女,漢族,博士,講師,從事擬周期動力系統的研究,E-mail:xiufangren@gmail.com.

國家自然科學基金(批準號:21364016)、新疆維吾爾自治區自然科學基金(批準號:20122111328)和新疆維吾爾自治區重點學科項目(批準號:2012ZDXK13).

http://www.cnki.net/kcms/detail/22.1340.O.20150211.1126.001.html.

O175.13

：A

：1671-5489(2015)03-0383-06