基于四元數EKF算法的小型無人機姿態估計

宋 宇,翁新武,郭昕剛

(長春工業大學 計算機科學與工程學院,長春 130012)

?

基于四元數EKF算法的小型無人機姿態估計

宋 宇,翁新武,郭昕剛

(長春工業大學 計算機科學與工程學院,長春 130012)

針對小型無人機設計的姿態測量系統,提出一種用于小型無人機姿態估計的四元數擴展Kalman濾波算法.該算法通過建立四元數姿態運動模型和航姿傳感器測量模型,構建了以四元數和陀螺儀隨機漂移為狀態向量、以加速度計測量值和磁阻儀解算的航向角為觀測向量的擴展Kalman濾波器,并設計了自適應測量噪聲協方差矩陣修正法.實驗結果表明,該算法不但解決了微機電系統慣性器件用于載體姿態測量時精度低、易發散、易被干擾的問題,而且顯著減小了陀螺儀隨機漂移對姿態估計的影響,有效提高了姿態估計的精度.

四元數；擴展Kalman濾波；姿態估計；微機電系統；小型無人機

實時、穩定、精準的姿態信息是無人機實現自主飛行和執行各種任務的基礎[1].受載荷和尺寸的限制,小型無人機(small UAV)通常不適合搭載高性能、體積大、價格高的傳統姿態測量系統.微機電系統(micro electro mechanical systems,MEMS)傳感器和嵌入式處理器由于其體積小、重量輕、功耗低等優點,在小型無人機慣性導航上應用廣泛.但MEMS慣性器件用于姿態估計時存在如下問題：1)陀螺儀存在漂移,單獨使用陀螺儀估計無人機姿態存在積累誤差；2)加速度計受線性加速度和振動影響較大,單獨利用加速度計估計載體姿態角,會出現較大誤差,動態時可信度較低；3)磁阻儀易受周圍環境(如高壓線、鐵礦廠等)所產生的磁場干擾,從而影響航向角的輸出.由于此類誤差是隨機的,無法預先消除,因此不能單獨通過上述方法獲取準確的姿態角,必須采用合理的數據融合方法以補償各類誤差帶來的影響,才能獲得穩定可靠的姿態信息[2-3].

描述飛行器姿態常用的方法有Euler角法、四元數法、方向余弦法和等效旋轉矢量法等.Euler角法描述簡單、無冗余參數,但存在奇異值,計算量大；方向余弦法可全姿態工作,但存在9個參數,求解計算量大；等效旋轉矢量法可消除計算的方向余弦矩陣或四元數中的不可交換性誤差,但存在大量參數冗余；四元數法因為計算量小、非奇異性、無超越函數和可全姿態工作等優點得到廣泛應用.文獻[4]提出了應用于便攜式移動機器人的四元數姿態解算方法,但未考慮傳感器的測量誤差會影響姿態估計;文獻[5]將MEMS傳感器數據通過四元數互補濾波器實現三自由度的姿態測量,有效減小了測量誤差,提高了測量精度;文獻[6-7]采用基于四元數的Kalman濾波器(Kalman filter,KF),進一步提高了姿態測量精度.但在實際應用中,飛行器姿態測量系統一般都是非線性系統,則基于系統線性Gauss分布的Kalman濾波器不能給出最優解,而擴展Kalman濾波器(extended Kalman filter,EKF)利用Taylor級數展開的方法將非線性系統線性化,進而采用Kalman濾波的基本步驟進行狀態估計更新[8].

本文在總結、分析常見姿態測量方法的基礎上,提出一種基于四元數擴展Kalman濾波器的小型無人機姿態測量方案.通過建立四元數姿態描述模型和MARG(magnetic,angular rate,and gravity)傳感器測量模型,構建了以四元數、陀螺儀零漂誤差為狀態向量、以加速度計和磁阻儀解算的航向角為觀測向量的擴展Kalman濾波器,為減小載體機動時和外界磁干擾對姿態測量的影響,設計了自適應的測量噪聲協方差矩陣,提高了姿態測量精度,實現了三自由度的姿態測量.最后通過實驗對上述算法進行了有效評估.

1 飛行器姿態運動模型

1.1參考坐標系

根據捷聯慣性導航原理[9],飛行器的姿態角就是載體坐標系b相對于導航坐標系n的方位關系.本文定義載體坐標系為OXbYbZb,該坐標系與機體固聯,原點選為飛行器質心,Xb軸沿機體橫軸指向右,Yb軸沿機體縱軸指向前,Zb軸垂直指向機體上方,且構成右手坐標系.定義地理坐標系OXnYnZn作為導航坐標系,該坐標系的原點在飛行器的質心,Xn,Yn和Zn軸分別從原點出發指向東、北和天向,簡稱ENU系.

1.2坐標系間的轉換

(1)

為坐標轉換矩陣,也稱為姿態矩陣.

(2)

由式(1),(2)可得載體的姿態角為

(3)

其中滾轉角φ和航向角ψ需要對主值進行相位判斷[10].

1.3四元數姿態運動模型

(4)

式中:ωx表示繞滾轉軸角速度;ωy表示繞俯仰軸角速度;ωz表示繞航向軸角速度.

采用一階Runge-Kutta法求解四元數微分方程[12],可得其離散時間模型為

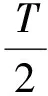
其中:T表示系統采樣時間間隔;q(k-1)表示k-1時刻四元數.設置初始四元數q(0),利用式(5)可遞推出第k時刻四元數q(k)的取值,進而更新姿態矩陣.

2 MARG傳感器誤差分析與校正

MARG傳感器由一個三軸MEMS陀螺儀、一個三軸MEMS加速度計和一個三軸MEMS磁阻儀組成,直接固聯在飛行器上,各傳感器內部量測坐標軸相互正交,且與載體坐標系重合,因此各傳感器輸出為三維矢量,對應的輸出為角速度ωb、加速度ab、磁場向量mb.

2.1誤差分析

使用MARG傳感器求解飛行器姿態時主要存在以下幾種誤差：1)傳感器的安裝誤差和標度誤差；2)陀螺儀的漂移和加速度計的零位誤差；3)初始條件誤差,包括導航參數和姿態角的初始誤差；4)計算誤差,主要包括量化誤差、用四元數求解姿態角和濾波算法的計算誤差；5)載體機動導致的動態誤差.其中前兩項由MARG傳感器導致,而由于MEMS傳感器精度較低,其誤差還包括測量噪聲.MARG傳感器輸出誤差將影響姿態的精度,所以有必要對其進行誤差校準.

2.2誤差校正

由于飛行器在運動過程中其姿態并非一直保持水平,因此還需對磁場測量值進行傾斜補償,得到水平磁場分布,磁場的水平分量為

由式(6),解算得到航向角ψ=arctan(myn/mxn).

3 擴展Kalman濾波器的設計

3.1系統結構

圖1 系統結構Fig.1 Block diagram of the system

姿態測量系統結構如圖1所示.為保證系統輸出的姿態角可靠、穩定,本文將陀螺儀、加速度計和磁阻儀測量值通過擴展Kalman濾波器進行多傳感器信息融合,求取姿態角、更新姿態矩陣,并設置自適應的測量噪聲協方差矩陣,提高姿態測量精度.

3.2系統模型

考慮非線性離散系統：

其中:x(k)∈n表示k時刻系統的狀態矢量;z(k)∈m表示k時刻系統的觀測矢量；f(·)表示實的n維矢量函數,h(·)表示實的m維矢量函數,f(·)和h(·)對其自變量都是非線性的；w(k)∈n和v(k)∈m是協方差分別為Q(k)和R(k)的過程噪聲矢量.

3.2.1 狀態方程 設系統狀態量為

(7)

其中:q0(k),q1(k),q2(k),q3(k)為姿態四元數；bωx(k),bωy(k),bωz(k)分別為繞滾轉軸、俯仰軸和航向軸的陀螺儀隨機漂移向量.則系統的狀態方程為

對f(x(k-1),k-1)求取Jacobi矩陣：

(9)

當飛行器靜止和勻速運動時,存在如下關系：

(10)

系統的觀測方程為

對h(x(k),k)求取Jacobi矩陣,可得系統量測矩陣為

3.3擴展Kalman濾波方程

根據擴展Kalman濾波理論,通過時間更新和量測更新的迭代求得系統狀態向量的最優估計,系統的擴展Kalman濾波遞推過程如下：

1)初始估計.計算狀態初始值x(0),設定過程噪聲協方差Q(k)、量測噪聲協方差R(k)和誤差方差矩陣P(0).

2)時間更新.計算狀態轉移函數的Jacobi矩陣：

(12)

從而k時刻狀態向量估計值為

更新狀態誤差協方差陣為

3.4擴展Kalman濾波修正

ca和cm為設定的權重因子.當載體線性加速度和外界磁干擾越大,相應的協方差也越大,此時狀態增益矩陣將減小,以減緩Kalman預測校準.

4 實 驗

本文采用的慣性測量單元(IMU)包括三軸加速度計、三軸陀螺儀(MPU-6050)、三軸磁阻儀(HMC5583L)和一個高性能FPGA微處理器(EP2C35F672C6).用微處理器對MARG傳感器測量的原始數據以1 000 Hz的采樣頻率進行采樣,在未濾波的情況下將原始數據通過串口發送至PC機,在PC機上利用MATLAB設計的擴展Kalman濾波器對數據進行處理,以獲取準確的姿態信息,最后將實驗結果用曲線描繪的方式顯示,并對解算結果進行比較分析.

為驗證本文姿態解算算法的有效性,分別進行3組實驗:1)IMU置于水平桌面靜止不動,如圖2所示；2)IMU做無規律運動,且有外界磁干擾,如圖3所示；3)IMU做無規律運動,有外界磁干擾,且增加高頻振動,如圖4所示.每組實驗都設計3種姿態解算法：利用加速度計和磁阻儀測量值的姿態解算法(G-M)(圖中黑色實線)；只采用陀螺儀的四元數姿態解算法(AR-Q)(圖中藍色雙線)；以及利用四元數EKF濾波將陀螺儀、加速度計和磁阻儀測量數據融合的姿態解算法(Q-EKF)(圖中紅色虛線).通過3組實驗對比3種算法在不同情況下的性能.

圖2 靜態時仿真結果Fig.2 Simulation results at static state

圖3 動態時仿真結果Fig.3 Simulation results at movement state

圖4 振動干擾時仿真結果Fig.4 Simulation results under vibration disturbance

由圖2可見,靜態時沒有其他線性加速度及干擾磁場,G-M算法能準確獲得載體的姿態信息；AR-Q算法會產生姿態角發散問題；而Q-EKF算法能有效地修正陀螺儀的隨機漂移誤差,解決了角度誤差累積的問題,準確地獲取了載體的姿態,且俯仰角和橫滾角都在0°附近,誤差控制在0.2°內.由圖3可見,動態時由于存在線性加速度及干擾磁場的影響,G-M算法獲得的載體姿態信息有時誤差會較大；AR-Q算法雖然不受線性加速度及干擾磁場的影響,但仍存在姿態角發散問題；而Q-EKF算法能有效減小載體線性加速度和干擾磁場的影響,且能有效地修正陀螺儀的隨機漂移誤差,動態性能較好.由圖4可見,當載體附加有高頻振動時,G-M算法得到姿態角有明顯的毛刺和突變分量,可能會導致載體的震蕩；AR-Q算法姿態角發散問題較嚴重；而Q-EKF算法有效地消除了干擾噪聲和突變分量,實現了姿態角的正確估計.

綜上所述,本文提出了一種適用于小型無人機姿態估計的四元數擴展Kalman濾波算法,將三軸陀螺儀、三軸加速度計和三軸磁阻儀的測量數據通過擴展Kalman濾波器進行信息融合,修正了陀螺儀的隨機漂移誤差,解決了角度誤差累積問題,能夠準確獲取載體的姿態.并設計了自適應量測噪聲協方差矩陣修正法,能有效抑制線性加速度和干擾磁場對姿態估計的影響,提高了姿態測量精度.實驗表明,本文提出的算法在靜態、動態時都能提供實時、穩定、精準的姿態信息.

[1] 房建成,張霄.小型無人機自動駕駛儀技術 [J].中國慣性技術學報,2007,15(6):658-663.(FANG Jiancheng,ZHANG Xiao.Development of Autopilot Technology of Small UAV [J].Journal of Chinese Inertial Technology,2007,15(6):658-663.)

[2] Tayebi A,McGilvray S,Roberts A,et al.Attitude Estimation and Stabilization of a Rigid Body Using Low-Cost Sensors [C]//Proceeding of the 46th IEEE Conference on Decision and Control.Berlin:Springer,2007:6424-6429.

[3] 秦勇,臧希喆,王曉宇,等.基于MEMS慣性傳感器的機器人姿態檢測系統的研究 [J].傳感技術學報,2007,20(2):298-301.(QIN Yong,ZANG Xizhe,WANG Xiaoyu,et al.Research of Attitude Estimation System Using MEMS Inertial Sensors [J].Chinese Journal of Sensors and Actuators,2007,20(2):298-301.)

[4] 張思奇,趙憶文.便攜式移動機器人姿態解算方法 [J].微計算機信息,2007,23(10-2):188-190.(ZHANG Siqi,ZHAO Yiwen.Attitude Algorithm of Portable Mobile Robot [J].Microcomputer Information,2007,23(10-2):188-190.)

[5] YUN Xiaoping,Lizarraga M,Bachmann E,et al.An Improved Quaternion-Based Kalman Filter for Real-Time Tracking of Rigid Body Orientation [C]//Proceedings of the IEEE International Conference on Intelligent Robots and Systems.Piscataway,NJ:IEEE,2003:1074-1079.

[6] Harms H,Amft O,Winkler R,et al.ETHOS:Miniature Orientation Sensor for Wearable Human Motion Analysis [C]//Proceedings of IEEE Sensors Conference.Piscataway,NJ:IEEE,2010:1037-1042.

[7] Yun X,Bachmann E,McGhee R.A Simplified Quaternion Based Algorithm for Orientation Estimation from Earth Gravity and Magnetic Field Measurements [J].IEEE Trans Instrum Meas,2008,57(3):638-650.

[8] 王松,田波,戰榆莉,等.基于修正EKF的微小型飛行器姿態估計 [J].高技術通訊,2011,21(6):612-618.(WANG Song,TIAN Bo,ZHAN Yuli,et al.Flight Attitude Estimation for MAVs Based on Amended EKF [J].Chinese High Technology Leters,2011,21(6):612-618.)

[9] 陳哲.捷聯慣導系統原理 [M].北京:宇航出版社,1996:82-85.(CHEN Zhe.The Principle of Strap Down Inertial Navigation System [M].Beijing:Astronautics Press,1996:82-85.)

[10] 秦永元.慣性導航 [M].北京:科學出版社,2006:297.(QIN Yongyuan.Inertial Navigation [M].Beijing:Science Press,2006:297.)

[11] Oshman Y,Carmi A.Attitude Estimation from Vector Observations Using Genetic Algorithm-Embedded Quaternion Particle Filter [J].Journal of Guidance,Control,and Dynamics,2006,29(4):879-891.

[12] 王鵬,呂顯瑞,張伸煦.求解隨機微分方程的三級半隱式隨機龍格庫塔方法 [J].吉林大學學報:理學版,2008,46(2):219-223.(WANG Peng,Lü Xianrui,ZHANG Shenxu.Three-Stage Semi-implicit Stochastic Runge-Kutta Methods for Stochastic Differential Equations [J].Journal of Jilin University:Science Edition,2008,46(2):219-223.)

[13] 劉興川,張盛,李麗哲,等.基于四元數的MARG傳感器姿態測量算法 [J].清華大學學報:自然科學版,2012,52(5):627-631.(LIU Xingchuan,ZHANG Sheng,LI Lizhe,et al.Quaternion-Based Algorithm for Orientation Estimation from MARG Sensors [J].Tsinghua Univ:Sci &Tech,2012,52(5):627-631.)

[14] Suh Y S.Orientation Estimation Using a Quaternion-Based Indirect Kalman Filter with Adaptive Estimation of External Acceleration [J].IEEE Trans Instrumentation and Measurement,2010,59(12):3296-3305.

[15] Bird J,Arden D.Indoor Navigation with Foot-Mounted Strap Down Inertial Navigation and Magnetic Sensors [J].IEEE Wireless Communcation,2011,18(2):28-35.

(責任編輯：韓 嘯)

SmallUAVAttitudeEstimationBasedontheAlgorithmofQuaternionExtendedKalmanFilter

SONG Yu,WENG Xinwu,GUO Xingang

(CollegeofComputerScienceandEngineering,ChangchunUniversityofTechnology,Changchun130012,China)

A new algorithm of quaternion extended Kalman filter was adopted to estimate the attitude of small UAV.After the establishment of the models of quaternion attitude movement and magnetic,angular rate,and gravity sensor measurement,a new designed extended Kalman filter was given with the quaternion and random drifting of gyro being the static vectors and the accelerometer measurements and the heading solved by the magnetometer being the observational vectors.What’s more,an innovation amendment method based on an adaptive approach to construct the measurement noise covariance matrix was designed.Experimental results show that the algorithm not only solves the problems of micro electro mechanical systems inertial sensors used for attitude measurement to show low accuracy and to be easy to diverge and to disturb,but also significantly reduces the effect of random drifting of gyro scope on attitude estimation,and proves to be effective at improving the accuracy of attitude estimation.

quaternion;extended Kalman filter;attitude estimation;micro electro mechanical systems (MEMS);small UAV

10.13413/j.cnki.jdxblxb.2015.03.31

2014-09-17.

宋 宇(1969—),男,漢族,碩士,副教授,從事嵌入式系統設計的研究,E-mail：songyu@mail.ccut.edu.cn.

教育部“春暉計劃”項目(批準號:Z2011139).

TP39

：A

：1671-5489(2015)03-0511-08