二能級原子自發輻射過程中的Wigner-Yanase偏態信息

劉萬芳,尹訓昌,付 靜,李 敏

(1.安慶師范學院 物理與電氣工程學院,安徽 安慶 246011;2.吉林建筑大學城建學院,長春 130111;3.集美大學誠毅學院,福建 廈門 351100)

?

二能級原子自發輻射過程中的Wigner-Yanase偏態信息

劉萬芳1,尹訓昌1,付 靜2,李 敏3

(1.安慶師范學院 物理與電氣工程學院,安徽 安慶 246011;2.吉林建筑大學城建學院,長春 130111;3.集美大學誠毅學院,福建 廈門 351100)

研究單個二能級原子自發輻射過程中原子和光場Wigner-Yanase的信息變化,并分別計算原子和輻射場的Wigner-Yanase信息.結果表明：原子和光場的Wigner-Yanase信息均依賴于平均值〈Sz〉;當原子處于基態時,光場的Wigner-Yanase信息達到最大值;原子與光場并非同步達到最大混合態.

二能級原子;自發輻射;Dicke模型;Wigner-Yanase偏態信息;混合態

自以量子糾纏為基礎的量子隱形傳態方案提出以來[1],量子信息科學已引起人們廣泛關注,在進行量子通訊[2]過程中,Wigner-Yanase偏態信息可較好地刻畫一個系統的信息量[3-4].純態中Wigner-Yanase偏態信息對應某個算符的漲落,若體系的量子態用密度算符描述,則其體現了某個算符與密度算符的不對易程度.由于Wigner-Yanase偏態信息是量子Fisher信息特殊的一類[5],因此其與不確定度[6-7]和系統參數估計及量子糾纏[8]有關.在2個量子比特純態中,通過定義一個廣義的Wigner-Yanase偏態信息,即與完全concurrence等價[9]；在多粒子體系中,通過粒子間的相互作用,可提高該體系的Wigner-Yanase偏態信息[9-10]；在量子記憶與信息存儲系統中,當光場信息轉移至原子系綜時,可通過Wigner-Yanase偏態信息刻畫光場信息的減少與原子系綜信息的增加[11].

光場與原子構成的復合系統在糾纏態的制備、糾纏度的濃縮、量子計算、量子態的保真和壓縮轉化中應用廣泛[12-15],但對復合系統及兩個子系統在光場與原子發生相互作用時的信息變化研究較少,本文針對單個處于激發態的二能級原子與真空場構成的復合系統,在原子自發輻射至基態的過程中,討論光場與原子兩個子系統Wigner-Yanase偏態信息的變化.

1 Wigner-Yanase偏態信息

文獻[16]利用局部的Wigner-Yanase偏態信息定義了量子關聯,若給定體系的狀態為ρ,則觀測量Ak的偏態信息表達式[3]為

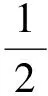
(1)

由式(1)可見:對于一個孤立體系,若其狀態變化遵守Landau-von Neumann方程,則該體系的信息保持一個常數；當兩個不同系綜合并時,聯合系綜的信息將小于分系綜信息的平均值；當兩個不同的組成部分構成復合系統時,復合系統的信息可分為兩部分信息之和.

式(1)體現了算符Ak和量子態ρ之間的不對易程度.對于純態,體系的狀態可用波函數ψ描述,若與波函數ψ對應的密度矩陣ρn=ρ,則偏態信息為

(2)

即算符Ak的漲落.

1.1單個量子比特總的Wigner-Yanase偏態信息

利用Bloch球表示單個量子比特,在退相干機制下,文獻[17]討論了量子Fisher信息的演化特性.若單個量子比特的總自旋為S,則相應的3個自旋算符Sx,Sy,Sz滿足的對易關系為

(3)

基于偏態信息的定義,引入一總偏態信息

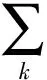
(4)

(5)

式(5)即為單個量子比特偏態信息的上限.若單個量子比特處于最大的混合態,則單個量子比特的偏態信息有一個為零的下限,由于最大混合態可用密度矩陣

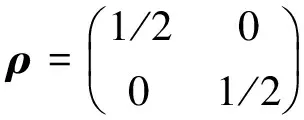
(6)

描述,且該密度矩陣與任何二維矩陣均具有對易的特點,因此

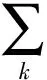
(7)

即處于最大混合態的單個量子比特有一個值為零的下限偏態信息.

1.2玻色系統總的Wigner-Yanase偏態信息

對于玻色系統,利用產生湮滅算符a+和a定義兩個厄米算符分別為

(8)

即算符X1和X2為描述玻色系統兩個正交分量的算符,并滿足對易關系

(9)

由偏態信息的定義可定義玻色系統的總偏態信息為

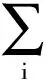
(10)

玻色系統純態的總偏態信息為

(11)

由于任意兩個粒子數態|m〉和|n〉等概率混合對應的密度矩陣并非與任意算符均對易,因此與二能級原子的情況不同.

2 單個二能級原子自發輻射過程中的偏態信息

在Weisskopf-Wigner自發輻射理論下,量子腔中一個處于激發態|+〉的原子可以任意頻率釋放一個光子而回到基態|-〉,原子與腔的相互作用可用Hamilton量[18]描述為

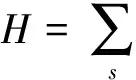
(12)

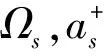
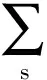
(13)

若原子初始時刻處于激發態|+〉,腔場處于真空態|0〉,則任意時刻腔場原子體系的狀態可表述為

(14)

將式(14)代入Schr?dinger方程可得概率幅c+(t)和c-,s(t)滿足的方程為

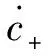
(15)

若所有的模式頻率接近,則式(13)中的求和可換為積分

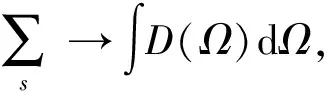
(16)

其中D(Ω)為終態態密度,該態密度和耦合強度g(Ω)分別與Ω的某次冪成比例.通過計算可得

(17)

其中γ與原子的壽命相關.

2.1二能級原子的偏態信息

通過對光場求跡計算原子的約化密度矩陣

(18)

可得原子的偏態信息,利用總的偏態信息定義,將3個算符對應的偏態信息相加可得

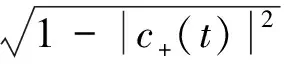
(19)

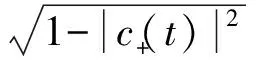
(20)

考慮到Sz的平均值為(cos2θ-sin2θ)/2,則可將式(20)轉化為

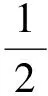
(21)

2.2輻射場的偏態信息

若處于激發態|+〉的原子可以任何頻率輻射一個光子回到基態|-〉,則光場以概率pssin2θ處于頻率為Ωs的|1s〉態,與其對應的密度矩陣為

(22)

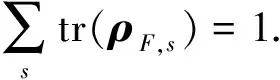
(23)

代入相應的數據,可得

(24)

由于光場所有模式之間沒有關聯,因此光場總的偏態信息為所有的It(ρF,s)相加,即

(25)

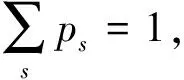
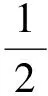
(26)

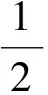
(27)

式(27)表明光場的偏態信息依賴于〈Sz〉.

二能級原子和光場偏態信息的演化特性如圖1所示,其中圖1(A)為Dicke模型,圖1(B)為J-C模型.由圖1(A)可見:在原子從激發態逐漸演化到最大混合態,最后演化到基態的過程中,原子信息經歷了一個從1/2逐漸變小到零,又逐漸增大到1/2的過程,如圖1(A)中實線所示;光場的偏態信息也經歷一個類似過程,但當原子信息回到1/2時,光場信息達到最大值3/2,如圖1(A)中虛線所示.當原子的偏態信息為零時,光場的偏態信息為初始值的1/2,即若將光場最小偏態信息對應的狀態作為最大混合態的標準,則一個光子和真空場等概率混合時,不是最大混合態,這不同于二能級原子的最大混合態.此外,在原子從激發態躍遷到基態的過程中,光子的平均個數為一個隨時間增加的函數,當原子處于基態時,光子個數應為1,比較光場的偏態信息曲線可見,光場的偏態信息依賴于光子的個數和光場的狀態.隨著時間的變化,原子最后穩定在基態,兩個子系統的信息均未出現反彈現象.在自發輻射過程中,兩個子系統之間不存在信息轉移、存儲和釋放等現象,與電磁誘導光透明系統的結果不同[11].

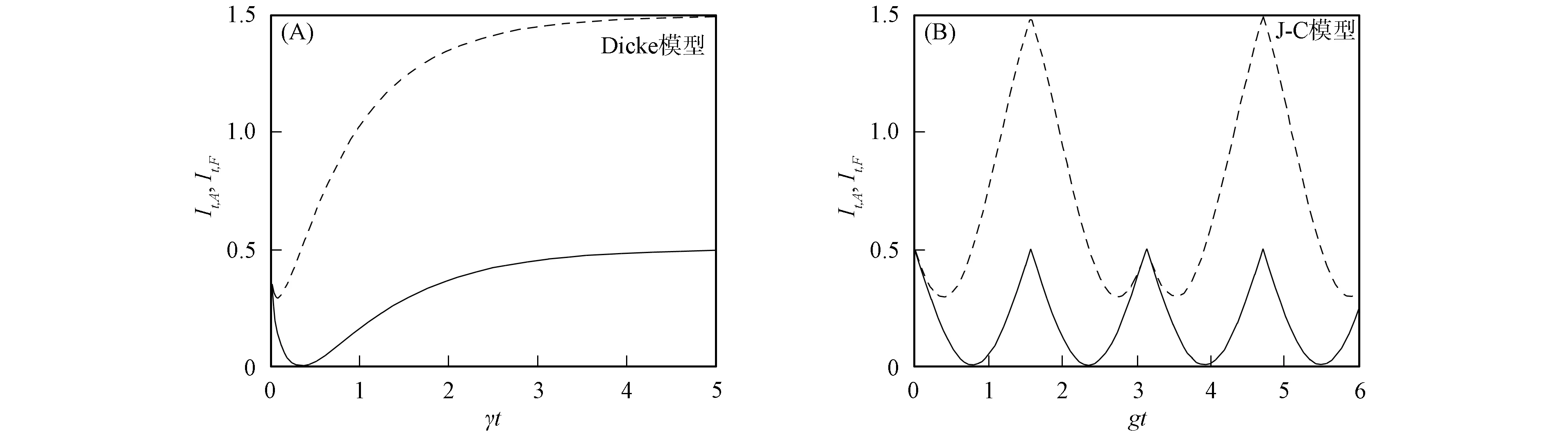
圖1 原子偏態信息It,A(實線)和光場偏態信息It,F(虛線)的演化特性Fig.1 Evolutions of skew information of atom It,A (solid line)and that of optical field It,F (dashed line)

若二能級原子的自發輻射過程采用J-C模型處理[18],則可得相似的結論：

(28)

其中θ=gt,g表示光場和二能級原子的耦合常數.Sz的平均值為(cos2θ-sin2θ)/2,將式(28)分別化為式(21)和式(27).由圖1(B)可見,二能級原子與光場的偏態信息呈周期性變化,但與Dicke模型所得結果不同.

綜上,本文研究了單個二能級原子從激發態自發輻射到基態過程中原子和光場的偏態信息,通過分析可得如下結論：

1)二能級原子在激發態和基態具有相同的Wigner-Yanase偏態信息,在最大混合態時Wigner-Yanase偏態信息達到最小值零.

2)光場的Wigner-Yanase偏態信息依賴于光場的平均光子數和光場的狀態;真空態|0〉和光子數態|1〉等概率混合時,偏態信息未達到最小值.

3)原子對光場的信息沒有存儲和釋放功能.

[1] Bennett C H,Brassard G,Crépeau C,et al.Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels [J].Phys Rev Lett,1993,70(13):1895-1900.

[2] Bouwmeester D,PAN Jianwei,Mattle K,et al.Experimental Quantum Teleportation [J].Nature,1997,390:575-579.

[3] Wigner E P,Yanase M M.Information Contents of Distributions [J].Proc Natl Acad Sci USA,1963,49(6):910-918.

[4] LUO Shunlong,FU Shuangshuang,Choo H O.Quantifying Correlations via the Wigner-Yanase Skew Information [J].Phys Rev A,2012,85(3):032117.

[5] LUO Shunlong.Wigner-Yanase Skew Information vs Quantum Fisher Information [J].Proceedings of the American Mathematical Society,2004,132(3):885-890.

[6] LUO Shunlong.Wigner-Yanase Skew Information and Uncertainty Relations [J].Phys Rev Lett,2003,91(18):180403.

[7] LUO Shunlong.Heisenberg Uncertainty Relation for Mixed States [J].Phys Rev A,2005,72(4):042110.

[8] CHEN Zeqiang.Wigner-Yanase Skew Information as Tests for Quantum Entanglement [J].Phys Rev A,2005,71(5):052302.

[9] LIU Wanfang,YIN Xunchang,ZHANG Lihua.Storage of Maximal Wigner-Yanase Skew Information of Two-Qubit System Using Nonlinear Interactions with Decay [J].Int J Theor Phys,2011,50(11):3375-3384.

[10] SUN Honggui,LIU Wanfang,LI Chunjie.Maximal and Total Skew Information for a Two-Qubit System Using Nonlinear Interaction Models [J].Chin Phys B,2011,20(9):090301.

[11] 付靜,劉萬芳,趙玉杰.電磁誘導光透明過程中Wigner-Yanase偏態信息 [J].物理學報,2013,62(17):170302.(FU Jing,LIU Wanfang,ZHAO Yujie.Wigner-Yanase Skew Information of the System with the Electromagnetically Induced Transparency [J].Acta Phys Sin,2013,62(17):170302.)

[12] 宋明玉,吳耀德.微波驅動雙模四能級單原子中連續變量糾纏的制備 [J].物理學報,2013,62(6):064207.(SONG Mingyu,WU Yaode.Generation of Continuous-Variable Entanglement in a Two-Mode Four-Level Single-Atom Driven by Microwave [J].Acta Phys Sin,2013,62(6):064207.)

[13] CAO Zhuoliang,ZHANG Lihua,YANG Ming.Concentration for Unknown Atomic Entangled States via Cavity Decay [J].Phys Rev A,2006,73(1):014303.

[14] DUAN Luming,GUO Guangcan.Scheme for Reducing Decoherence in Quantum Computer Memory by Transformation to the Coherence-Preserving States [J].Chin Phys Lett,1997,14(7):488-491.

[15] Poulsen U V,Mφlmer K.Squeezed Light from Spin-Squeezed Atoms [J].Phys Rev Lett,2001,87(12):123601.

[16] Davide G,Tommaso T,Gerardo A.Characterizing Nonclassical Correlations via Local Quantum Uncertainty [J].Phys Rev Lett,2013,110(24):240402.

[17] ZHONG Wei,SUN Zhe,MA Jian,et al.Fisher Information under Decoherence in Bloch Representation [J].Phys Rev A,2013,87(2):022337.

[18] Scully M O,Zubairy M S.Quantum Optics [M].Cambridge:Cambridge University Press,2000.

(責任編輯：王 健)

Wigner-YanaseSkewInformationintheProcessofSpontaneousEmissionbetweenTwoAtomicLevels

LIU Wanfang1,YIN Xunchang1,FU Jing2,LI Min3

(1.SchoolofPhysicsandElectricEngineering,AnqingTeachersCollege,Anqing246011,AnhuiProvince,China;2.TheCityCollegeofJilinJianzhuUniversity,Changchun130111,China;3.JimeiUniversityChengyiCollege,Xiamen351100,FujianProvince,China)

We investigated the changes of the Wigner-Yanase information in the processes of the spontaneous emission of a two-level atom system,and calculated the Wigner-Yanase information for the reduced density matrix of the atom and that for the quantum radiation respectively.Our investigations show that both of them depend on the expectation of 〈Sz〉.And the Wigner-Yanase information for the radiation field reach the maximum when the atom stays in the ground state.Additionally,the results also show that both the atom and the field will not simultaneously become the maximal mixed state.

two-level atom;spontaneous emission;Dicke mode;Wigner-Yanase skew information;mixed state

10.13413/j.cnki.jdxblxb.2015.03.36

2014-07-18.

劉萬芳(1979—),男,漢族,碩士,副教授,從事量子信息的研究,E-mail:lwf2002251@126.com.通信作者:李 敏(1980—),女,漢族,碩士,講師,從事量子信息的研究,E-mail:190930259@qq.com.

安徽省自然科學基金(批準號:1408085QA15)和福建省中青年教師教育科研基金(批準號:JB14219).

O431.2

：A

：1671-5489(2015)03-0542-05