C2?C3中Bell基型不可拓展的最大糾纏基和互不偏基
楊 強,陶元紅,南 華,張 軍
(延邊大學 理學院數學系,吉林 延吉 133002)
?
C2?C3中Bell基型不可拓展的最大糾纏基和互不偏基
楊 強,陶元紅,南 華,張 軍
(延邊大學 理學院數學系,吉林 延吉 133002)
先在C2?C3中得到一組Bell基型完備的不可拓展的最大糾纏基,再通過構造C3的一個標準正交基給出另一組Bell基型完備的不可拓展的最大糾纏基,同時保證這兩組基是互不偏的,并給出兩類Bell基型互不偏的不可拓展的最大糾纏基.
Bell基型;最大糾纏態;互不偏基;不可拓展的最大糾纏基
0 引 言
自從多體量子系統中引入一組不可拓展的直積基(UPB)概念以來,人們已獲得了大量有實際應用價值的理論成果[1-2].UPB是一個由不完備正交直積基構成的集合,在其互補空間中沒有直積態,包含UPB的態不能被局部測量和經典計算區分,且在與一組UPB互補子空間上的混合態是一個束縛糾纏態[3].將UPB推廣到不可拓展的最大糾纏基(UMEB),即UMEB是一個Cd?Cd上由標準正交最大糾纏態構成的集合,該集合含有向量小于d2個,且不存在其他的與其均正交的最大糾纏向量.當d=2時,不存在UMEB.當d=3,4時,存在含6個向量和12個向量的UMEB[4].
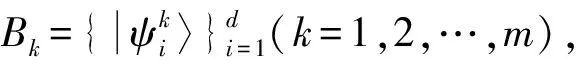
其中k,k′=1,2,…,m,則稱{B1,B2,…,Bm}為互不偏基(MUBs)[5].MUBs主要用于解決量子態層析和加密協議等問題[6-10],其個數N(d)最多不超過d+1.當d為一個素數冪時,N(d)=d+1;當d為一個非素數冪的合數時,N(d)未知[6].關于N(6)及在C6上如何構造MUBs的研究目前已引起人們廣泛關注[11-14].本文先證明兩體空間C2?C3上Bell基型的UMEB,通過構造C3的一個標準正交基給出兩組Bell基型完備的UMEBs,同時保證這兩組基是MUBs,并給出兩類互不偏的不可拓展的最大糾纏基集合.
1 C2?C3中Bell基型的UMEBs
定義1[3]一組態{|φi〉∈Cd?Cd′,i=1,2,…,n,n 1)|φi〉(i=1,2,…,n)均為最大糾纏態; 2)〈φi|φj〉=δij; 3)若〈φi|ψ〉=0(i=1,2,…,n),則|ψ〉不能為最大糾纏態. 當d=2,d′=3時,Bell基型的4個態為 (1) 其中{|0〉,|1〉},{|0′〉,|1′〉,|2′〉}分別為C2和C3中的標準正交基.顯然式(1)符合定義2,即|φi〉(i=0,1,2,3)均為最大糾纏態,且滿足〈φi|φj〉=δij(i,j=0,1,2,3). 下面證明式(1)中Bell基型的4個態滿足定義1中的條件3).即若存在一個態|ψ〉,使得〈φi|ψ〉=0(i=0,1,2,3),則|ψ〉一定不是最大糾纏態. 若假設|ψ〉為糾纏態,則|ψ〉可分解為 其中:λ0>0,λ1>0,λ0+λ1=1; U和V均為酉矩陣. 由〈φ0|ψ〉=0可得 整理得 (2) 同理由〈φi|ψ〉=0(i=1,2,3),可得: 分別整理得: (3) (4) (5) 方程(2)~(5)用矩陣可表示為 綜上所述,式(1)為C2?C3中一組不完備的四元UMEB. 在式(1)中加入兩個直積態|φ4〉=|02′〉和|φ5〉=|12′〉,即可得C2?C3一組完備的UMEB: (6) 構造C3的一個標準正交基: 重復使用上述方法可得C2?C3的另一組Bell基型完備的UMEB: (7) 由于 (8) 所以兩個完備Bell基型的UMEBs為MUBs. 將式(6)和式(7)中的兩個直積態分別換為文獻[3]中的|φ4〉,|φ5〉和|ψ4〉,|ψ5〉,可得兩組完備Bell基型的UMEBs和MUBs,即 (9) (10) 由Bell基型的4個態(1)為C2?C3中一組不完備的四元UMEB可知式(9)和式(10)均為完備Bell基型的UMEBs.通過計算可知式(9)和式(10)也為MUBs.如 對式(9)和式(10)中的直積態表達式進一步推廣可得: (11) 其中α,β均為實數,且滿足α2+β2=1. (12) 式(11)和式(12)均為完備Bell基型的UMEBs,通過計算可知式(11)和式(12)也為MUBs.由于 (13) 所以兩類完備Bell基型的UMEBs為MUBs. [1] Bennett C H,DiVincenzo D P,Mor T,et al.Unextendible Product Bases and Bound Entanglement [J].Phys Rev Lett,1999,82(26):5385-5388. [2] DiVincenzo D P,Mor T,Shor P W,et al.Unextendible Product Bases,Uncompletable Product Bases and Bound Entanglement [J].Commun Math Phys,2003,238(3):379-410. [3] CHEN Bin,FEI Shaoming.Unextendible Maximally Entangled Bases and Mutually Unbiased Bases [J].Phys Rev A,2013,88(3):034301. [4] Bravyi S,Smolin J A.Unextendible Maximally Entangled Bases [J].Phys Rev A,2011,84(4):042306. [5] Brierley S,Weigert S,Bengtsson I.All Mutually Unbiased Bases in Dimensions Two to Five [J].Quantum Information and Computation,2010,10(9/10):803-820. [6] Wootters W K,Fields B D.Optimal State-Determination by Mutually Unbiased Measurements [J].Ann Phys,1989,191(2):363-381. [7] Adamson R B A,Steinberg A M.Improving Quantum State Estimation with Mutually Unbiased Bases [J].Phys Rev Lett,2010,105(3):030406. [9] Cerf N J,Bourennane M,Karlsson A,et al.Security of Quantum Key Distribution Usingd-Level Systems [J].Phys Rev Lett,2002,88(12):127902. [10] Yu I C,Lin F L,Huang C Y.Quantum Secret Sharing with Multilevel Mutually (Un)biased Bases [J].Phys Rev A,2008,78(1):012344. [11] Brierley S,Weigert S.Maximal Sets of Mutually Unbiased Quantum States in Dimension 6 [J].Phys Rev A,2008,78(4):042312. [12] Brierley S,Weigert S.Constructing Mutually Unbiased Bases in Dimension Six [J].Phys Rev A,2009,79(5):052316. [13] Raynal P,Lü Xin,Englert B G.Mutually Unbiased Bases in Six Dimensions:The Four Most Distant Bases [J].Phys Rev A,2011,83(6):062303. [14] McNulty D,Weigert S.The Limited Role of Mutually Unbiased Product Bases in Dimension 6 [J].J Phys A:Math Theor,2012,45(10):102001. [15] Li Z G,Zhao M J,Fei S M,et al.Mixed Maximally Entangled States [J].Quantum Information and Computation,2012,12(1/2):63-73. (責任編輯:王 健) Bell-Base-TypeUnextendibleMaximallyEntangledBasesandMutuallyUnbiasedBasesinC2?C3 YANG Qiang,TAO Yuanhong,NAN Hua,ZHANG Jun (DepartmentofMathematics,CollegeofScience,YanbianUniversity,Yanji133002,JilinProvince,China) A complete Bell-base-type unextendible maximally entangled basis inC2?C3was proved.Based on a constructed orthonormal basis inC3,another complete Bell-base-type unextendible maximally entangled basis was constructed,which is mutually unbiased with the first one.Finally,two classes of Bell-base-type unextendible maximally entangled bases which are mutually unbiased were presented. Bell-base-type;maximally entangled state;mutually unbiased basis;unextendible maximally entangled basis 10.13413/j.cnki.jdxblxb.2015.03.37 2014-05-26. 楊 強(1991—),男,漢族,碩士研究生,從事量子力學及應用泛函分析的研究,E-mail:584431092@qq.com.通信作者:張 軍(1957—),男,漢族,教授,從事量子力學及應用泛函分析的研究,E-mail:zhangjun@ybu.edu.cn. 國家自然科學基金(批準號:11361065)和吉林省自然科學基金(批準號:201215239). O413.1 :A :1671-5489(2015)03-0547-06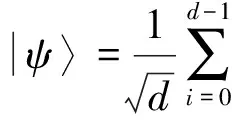
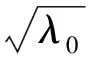
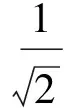
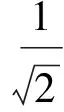
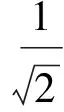
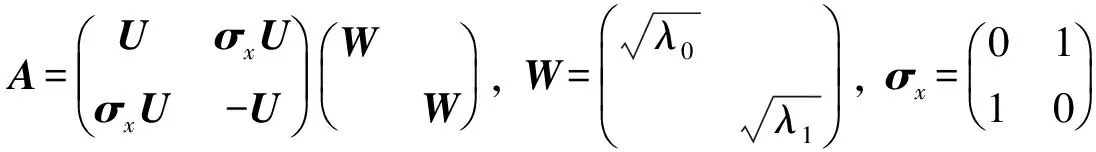
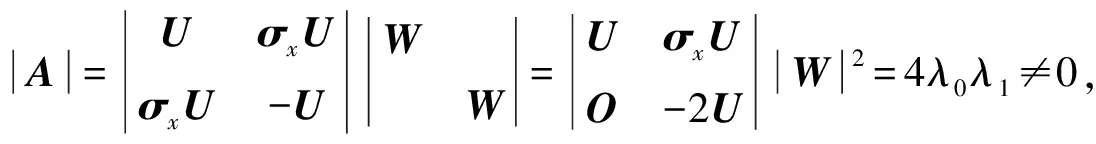
2 用C2?C3的UMEBs構造MUBs
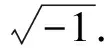
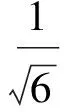
3 C2?C3中兩類互不偏的UMEBs
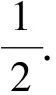
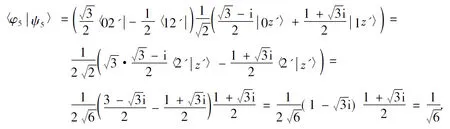
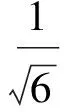
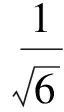
4 討 論