集值優(yōu)化問題廣義近似解的性質(zhì)和最優(yōu)性條件*1

王定暢, 仇秋生

(浙江師范大學(xué) 數(shù)理與信息工程學(xué)院,浙江 金華 321004)

集值優(yōu)化問題廣義近似解的性質(zhì)和最優(yōu)性條件*1

王定暢, 仇秋生

(浙江師范大學(xué) 數(shù)理與信息工程學(xué)院,浙江 金華 321004)

引進了集值優(yōu)化問題的一種廣義近似解,統(tǒng)一了其他集值優(yōu)化問題的近似解,研究了廣義近似解的性質(zhì),獲得了廣義近似弱有效解的最優(yōu)性條件.

集值優(yōu)化;廣義近似解;最優(yōu)性條件;拉格朗日乘子定理

0 引 言

優(yōu)化模型一般都是實際問題的簡化表示.利用數(shù)值算法得到的解大多是近似解,特別在約束集非緊的情況下,有效解集(或弱有效解集)往往是空集,但近似解集在很弱的條件下都是非空的.因此,研究近似解集不僅有理論價值而且有實際意義.1979年,Kutateladz[1]首次提出了非控近似解的概念;Loridan[2]提出了擬近似解的概念.注意到近似解的集合太大,White[3]對多目標(biāo)優(yōu)化問題提出了5種近似有效解的概念;1995年,Tanaka[4]在賦范空間中引進了一種具有度量一致性質(zhì)的近似解;1996 年,Yokoyama[5]討論了Kutateladz,White和Tanaka意義下的近似解之間的聯(lián)系;2006年,Gutierrez等[6]通過引進co-radiant集的概念定義了一個新的近似解的概念;2010 年,Gutierrez等[7]對序錐為閉凸錐的多目標(biāo)優(yōu)化問題引進了廣義擬近似解;2012 年,高英等[8]對向量優(yōu)化問題引進了一個更一般的近似有效解概念.

隨著集值優(yōu)化的發(fā)展,集值優(yōu)化問題的近似解引起了許多學(xué)者的興趣.1998年,陳光亞等[9]引進了集值優(yōu)化問題的近似有效解;戎衛(wèi)東等[10]引進了集值優(yōu)化問題的近似弱有效解的概念;2011年,Gutierrez等[11]引進了更一般的G(ε)解.

綜上所述,人們主要研究了向量優(yōu)化問題的近似解及集值優(yōu)化問題的近似有效解、近似弱有效解、近似Henig有效解,而對于集值優(yōu)化問題更一般的擬近似解的研究并不多.因此,如何提出集值優(yōu)化問題的擬近似解和更廣義的近似解,在比較弱的條件下獲得存在性定理及最優(yōu)性條件,是一個值得研究的課題.本文在文獻[8]的基礎(chǔ)上,將廣義近似解推廣到集值優(yōu)化問題,獲得了更一般的近似解.

1 相關(guān)概念及引理

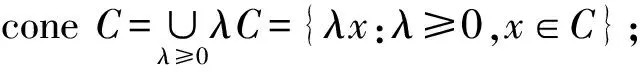
K+={l∈Y*:l(c)≥0,?c∈C};K+i={l∈Y*:l(c)>0,?c∈C}.

考慮下面帶約束的集值優(yōu)化問題:

其中:F:X→2Y;S?X且S≠?.若S=X,則(VPC)為無約束集值優(yōu)化問題，記為

若無特別說明,總假設(shè)K是Y中內(nèi)部非空的點凸錐,定義由K誘導(dǎo)出Y的偏序,即

x≤y??y-x∈K.

2 集值優(yōu)化問題的廣義近似解

設(shè)G是Y中的非空子集,滿足0?clG,G∩(-K)=?.設(shè)φ:R+→R+為一非降的實值函數(shù),滿足φ(0)=0,φ(t)>0.記b=(G,φ).對于任意固定點x0∈X,定義集值映射φ:X→2Y,φx0(x)=φ(d(x,x0))G.

定義1[9]設(shè)ε>0,q∈K,則

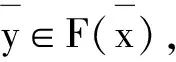
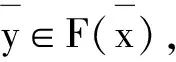
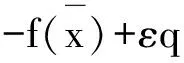
定義3[8]設(shè)f是X→Y的單值映射,ε≥0.

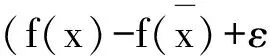
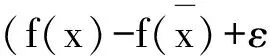
定義4設(shè)ε≥0.

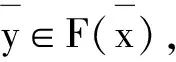
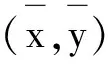
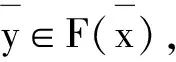
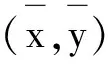
注11)若取ε=0,則(VPC)相對于b的廣義近似有效解和廣義近似弱有效解即為集值優(yōu)化問題的有效解和弱有效解.

2)若取φ(t)=1,?t≥0,并設(shè)G∩K≠?,則對?α∈G∩K,(VPC)相對于b的廣義近似有效解和廣義弱有效解即為定義1中的ε-有效解和ε-弱有效解.

3)設(shè)X是線性賦范空間,將F退化為單值映射,令q∈K{0},G={q},φ(d(x,y))=φ(‖x-y‖)=‖x-y‖,?x,y∈X,則相對于b的廣義近似有效解即為定義2中的擬(ε,q)-有效解.

4)若將F退化為單值映射,則(VPC)相對于b的廣義近似有效解和廣義近似弱有效解即為定義3中的廣義ε-有效解和廣義ε-弱有效解.

3 廣義近似有效解和廣義近似弱有效解的一些性質(zhì)

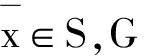
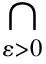
3)AE(F,K,b,ε1)?AE(F,K,b,ε2),?ε2>ε1>0;

4)若G1?G+K,則I(F,K,b,ε)?I(F,K,b1,ε),?ε>0,其中, b1=(G1,φ),I={AE,WAE};

5)若φ(t)≤φ1(t),?t≥0,則I(F,K,b,ε)?I(F,K,b2,ε),?ε>0,其中b2=(G,φ1),I={AE,WAE};

6)設(shè)b3=(G+K,φ),則I(F,K,b,ε)=I(F,K,b3,ε),其中I={AE,WAE}.

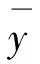
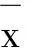
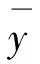
2)類似于1)的證明,故略.

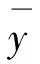
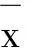
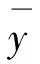
由K是凸錐知

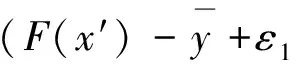
與式(2)矛盾,結(jié)論得證.

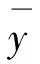
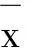
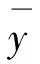
由于G1?G+K,故e′=e″+t,e″∈G,t∈K,代入式(4)有

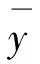
由K是凸錐知

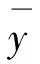
與式(3)矛盾.當(dāng)I=AE,同理可證.故結(jié)論得證.

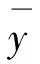
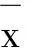
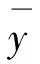
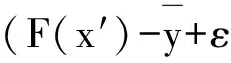
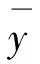
與式(5)矛盾.當(dāng)I=AE時,同理可證.結(jié)論得證.

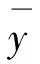
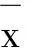
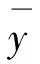
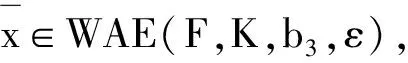
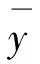
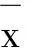
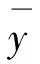
在式(7)中令t=0,有

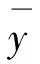
與式(8)矛盾.因此,WAE(F,K,b,ε)?WAE(F,K,b3,ε).類似可證當(dāng)I=AE時也成立.結(jié)論得證.命題1證畢.

命題2(拓?fù)湫再|(zhì)) 設(shè)X是線性度量空間,S?X是非空閉集,F:X→2Y上半連續(xù).

1)若WAE(F,K,b,ε)≠?,則WAE(F,K,b,ε)是閉集.

2)若S為緊集，則WAE(F,K,b,ε)為緊集.

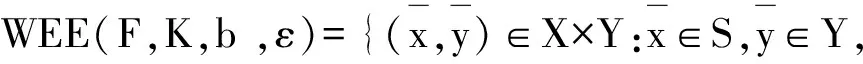
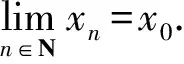
2)若S為緊集,則由1)知WAE(F,K,b,ε)是閉集,故易知WAE(F,K,b,ε)為緊集.

3)任取WEE(F,K,b,ε)中收斂的網(wǎng){(xα,yα)}α∈I, 記(xα,yα)→(x0,y0).由S是閉集知x0∈S.

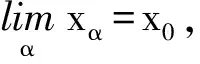
再證(x0,y0)∈WEE(F,K,b,ε).若不然,則對上述y0,存在x′∈S,e∈G,y′∈F(x′), 使得y′-y0+εφ(d(x′,x0))e∈-intK.

由φ的連續(xù)性知y′-yα+εφ(d(x′,xα))e→y′-y0+εφ(d(x′,x0))e,且-intK是開集,與(xα,yα)∈WEE(F,K,b,ε)矛盾.因此,(x0,y0)∈WEE(F,K,b,ε),即WEE(F,K,b,ε)是閉集.命題2證畢.

4 廣義近似解的最優(yōu)性條件

對集值映射F：X→2Y,若?x,y∈X,λ∈[0,1], 有λF(x)+(1-λ)F(y)?F(λx+(1-λ)y)+K,則稱集值映射F為凸的

注2易知若集值映射F：X→2Y為凸的,從而F(X)+K為凸集.

命題3設(shè)X是Banach空間,G?K是凸集，F(xiàn)是凸的,且φ是正齊次次可加的.任取x0∈X,定義集值映射φx0(x)=φ(d(x,x0))G.則F+εφx0是凸集值映射.

證明 任取x1,x2∈X,y1∈F(x1),y2∈F(x2),e1,e2∈G,λ∈(0,1).由φ正齊次和次可加知

λφ(d(x1,x0))+(1-λ)φ(d(x2,x0))≥φ(d(λx1+(1-λ)x2,x0)).

下證

y1+(1-λ)y2+λφ(d(x1,x0))e1+(1-λ)φ(d(x2,x0))e2∈F(λx1+(1-λ)x2)+

εφx0(λx1+(1-λ)x2)+K.

由題意知，

λφ(d(x1,x0))e1+(1-λ)φ(d(x2,x0))e2=(λφ(d(x1,x0))+(1-λ)φ(d(x2,x0)))e3.

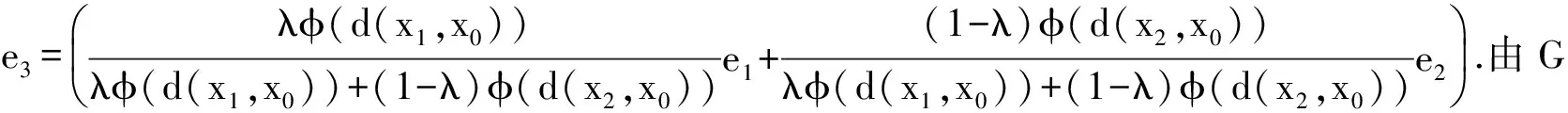
λy1+(1-λ)y2+λφ(d(x1,x0))e1+(1-λ)φ(d(x2,x0))e2=

λy1+(1-λ)y2+(λφ(d(x1,x0))+(1-λ)φ(d(x2,x0)))e3=

λy1+(1-λ)y2+(φ(d(λx1+(1-λx2),x0)))e3+(λφ(d(x1,x0))+(1-λ)φ(d(x2,x0))-

φ(d(λx1+(1-λx2),x0)))e3∈F(λx1+(1-λ)x2)+εφx0(λx1+(1-λ)x2)+K,

即得F+εφx0是凸集值映射.命題3證畢.

定理1(擇一性定理) 設(shè)X是Banach空間,G?K是凸集，F(xiàn)是凸的,且φ是正齊次次可加的,則以下結(jié)論有且僅有一個成立:

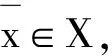
2)存在l∈K+{0},使得l(y0)≤l(y)+εφ(d(x,x0))l(e),?x∈X,y∈F(x),e∈G.

證明 易知若1)成立,則2)不成立.下證若1)不成立,則2)成立,即對?x∈X,(F(x)-y0+εφx0(x))∩(-intK)=?.由K是凸錐知(F(X)-y0+εφx0(X)+K)∩(-intK)=?.又由命題3和注2知F(X)+εφx0(X)+K是凸集.由凸集分離定理知,存在l∈Y*{0},使得

下證l∈K+{0}.若不然,則存在c0∈K,使得l(c0)<0.由K是凸錐知,固定y,q,e,?λ>0,有

在式(10)中令λ→+∞,即得l(-q)=-∞,矛盾.故l∈K+{0}.在式(9)中令c→0,q→0,得

l(y0)≤l(y)+εφ(d(x,x0))l(e), ?x∈X,y∈F(x),e∈G.

因此,2)成立.定理1證畢.

定理2設(shè)定理1中的條件均滿足,則(x0,y0)是(VP)問題關(guān)于b的廣義近似弱有效元當(dāng)且僅當(dāng)存在l∈K+{0},使得

證明 若(x0,y0)是(VP)關(guān)于b的廣義近似弱有效元,則由定理1知存在l∈K+{0},使得

又由y0∈F(x0)+εφx0(x0)知式(12)的右端可達到下確界,即

inf{l(z) :z∈F(x)+εφx0(x),x∈X}=l(y0).

反之,若存在l∈K+{0},使得

inf{l(z) :z∈F(x)+εφx0(x),x∈X}=l(y0).

而(x0,y0)不是(VP)關(guān)于b 的廣義近似弱有效解.因此,對上述y0,存在x′∈X,y′∈F(x′),e′∈G,使得y′-y0+εφ(d(x′,x0))e′∈-intK,故l(y′)+εφ(d(x′,x0))l(e′)

5 拉格朗日乘子定理

設(shè)Z是拓?fù)湎蛄靠臻g,G′:X→2Z是一集值映射,D為Z中的一內(nèi)部非空的凸錐,K內(nèi)部非空.記B(Z,Y)為Z→Y的所有連續(xù)線性算子,B+={s∈B(Z,Y) : s(D)?K}.現(xiàn)考慮集值優(yōu)化問題

其中,A={x∈X : G′(x)∩(-D)≠?}.

定理3設(shè):

1)(x0,y0)是(VP)關(guān)于b的廣義近似弱有效元;

2)G′(X)∩(-intD)≠?;

3)F+εφx0和G′是凸集值映射.

則存在s∈B+(Z,Y),使得(x0,y0)是以下問題關(guān)于b的廣義近似弱有效元:

(LP) {minF(x)+s(G′(x))+εφx0(x) : x∈X}.

且存在z0∈G′(x0),使得s(z0)=0.

證明 由于(x0,y0)是(VP)關(guān)于b的廣義近似弱有效元,故對?x∈A,有

(F(x)-y0+εφ(d(x,x0))G)∩(-intK)=?.

而?x?A,G′(x)∩(-D)=?,故

((F-y0+εφx0)(X),G′(X))∩(-intK,-intD)=?.

又由(F+εφx0,G′)是凸集值映射知((F-y0+εφx0)(X)+K,G′(X)+D)是凸集,且

((F-y0+εφx0)(X)+K,G′(X)+D)∩(-intK,-intD)=?.

由定理1知存在(η,l)∈(K+,D+){0,0},使得

由G′(x0)∩(-D)≠?知,可任取z0∈G′(x0)∩(-D).令x=x0,y=y0,z=z0,代入式(13)得l(z0)≥0.又由l∈D+,z0∈-D知l(z0)≤0.因此,l(z0)=0.

由K內(nèi)部非空知可取c∈K,l(c)=1.定義s(z)=l(z)c,?z∈Z.易知s是Z→Y的連續(xù)線性算子,且滿足s(D)=l(D)c?K.因此,s∈B+(Z,Y).由s(z0)=l(z0)c=0,?z0∈G′(x0)∩(-D),可得0∈s(G′(x0))，故

y0∈F(x0)?F(x0)+s(G′(x0))+εφx0?F(X)+s(G′(X))+εφx0(X).

對?x∈X,y∈F(x),z∈G′(x),e∈G,有

下證(x0,y0)是(LP)問題相對于b的廣義近似弱有效元.反證,若不然,則對上述y0,存在x′∈X,y′∈F(x′),e′∈G,z′∈G′(x′),使得

(y′-s(z′)+εφ(d(x′,x0))e′-y0)∩(-intK)≠?.

因此,η(y0)>η(y′)+l(z′)+εφ(d(x′,x0))η(e′).與式(14)矛盾.定理3證畢.

[1]Kuatateladze S S.Convexε-programing[J].Sov Math Dokl,1979,20(2):391-393.

[2]Lordian P.ε-solution in vector minimization problem[J].J Optim Theory Appl,1984,43(2):265-272.

[3]White D J.Epsilon efficiency[J].J Optim Theory Appl,1986,49(2):319-337.

[4]Tanaka T.A new approach to approximation of solutions in vector optimization problems[C]//Fushimi M T.Proceedings of APORS.Singapore:World Scientific,1995:497-504.

[5]Yokoyama K.Epsilon approximate solutions for multiobjective programming problems[J].J Math Anal Appl,1996,203(1):497-504.

[6]Gutierrez C,Jimenez B,Novo V.A unified approach and optimality conditions for approximate solutions of vector optimization problems[J].SIAM J Optim Theory Appl,2006,17(3):688-710.

[7]Gutierrez C,Lopez V,Novo V.Generalized quasi-solutions in multioblective optimization problems:Existence result and optimality conditions[J].Nonlinear Anal,2010,72(11):97-120.

[8]Gao Y,Hou S H,Yang X M.Existence and optimality conditions for approximate solutions to vector optimization problems[J].J Optim Theory Appl,2012,152(1):97-120.

[9]Chen Guangya,Huang X X.Ekeland′sε-variational principle for set-valued mappings[J].Math Method Oper Res,1998,48(1):181-186.

[10]Rong W D,Wu Y N.ε-weak minimal solutions for vector optimization problems with set-valued maps[J].J Optim Theory Appl,2000,106(3):569-579.

[11]Gutierrez C,Jimenez B,Novo V.A generic approach to approximate efficiency and applications to vector optimization with set-valued maps[J].J Global Optim,2011,49(2):313-342.

[12]Beldiman M,Panaitescu E,Dogaru L.Approximate quasi efficient solutions in multiobjective optimization[J].Bull Math Soc Sci Math Roum,2008,99(2):109-121.

(責(zé)任編輯 陶立方)

Thepropertiesandoptimalityconditionsforgeneralizedapproximatesolutionstoset-valuedoptimizationproblems

WANG Dingchang, QIU Qiusheng

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

A new concept of generalized approximate solution to set-valued optimization problems was introduced in order to unify the other apprximate solutions which had been inverstigated before. Some properties of generalized approximate solution were studied, and the optimality conditions for generalized approximate weak efficient solution were proposed.

set-valued optimization; generalized approximate solution; optimality condition; Lagrange multiplier theorem

10.16218/j.issn.1001-5051.2015.02.006

2014-05-11

國家自然科學(xué)基金資助項目(11471291)

王定暢(1989-)，男，浙江蘭溪人，碩士研究生.研究方向：最優(yōu)化理論.

仇秋生.E-mail: qsqiu@zjnu.cn

O221.6

A

1001-5051(2015)02-0156-07