路與圈的笛卡爾乘積的配對控制數*1

黃海圓, 馬美杰

(浙江師范大學 數理與信息工程學院,浙江 金華 321004)

路與圈的笛卡爾乘積的配對控制數*1

黃海圓, 馬美杰

(浙江師范大學 數理與信息工程學院,浙江 金華 321004)

根據Pn×Cm的結構特點,利用配對控制數的定義、歸納法及反證法,確定了路與圈的笛卡爾乘積圖Pn×Cm(m=3,4)的配對控制數.

笛卡爾乘積;控制集;控制數;配對控制集;配對控制數

本文僅討論無環、無重邊、無孤立點的無向圖.設G=(V,E)是頂點集為V、邊集為E的圖.圖G中的一個頂點u的開鄰域為N(u)={v∈V|uv∈E},點u的閉鄰域為N[u]=N(u)∪{u}.稱G中與u相關聯的邊的條數為u在G中的度數.記Δ(G)為G的最大度.圖G′=(V′,E′)是圖G=(V,E)的生成子圖,其中E′?E,V′=V.匹配M是G中兩兩不相鄰的邊組成的集合.若?v∈V,M中都有邊關聯v,則稱M是G的一個完美匹配.非空子集D?V,若對?x∈VD都有N(x)∩D≠?成立,則稱D是G的控制集.稱G中控制集的最小基數為G的控制數,記為γ(G).若D是控制集,且由D導出的子圖G[D]包含一個完美匹配M,則稱D是配對控制集.稱G中最小配對控制集的頂點數為G的配對控制數,記為γp(G).稱匹配M中的邊連接的2個點為D的對.G×H是2個圖G=(V1,E1)和H=(V2,E2)的笛卡爾乘積圖,V(G×H)={(u,v) |u∈V1,v∈V2}.其中,(u,v),(u′,v′)相鄰當且僅當u=u′且vv′∈E2,或者v=v′且uu′∈E1.

關于圖的笛卡爾乘積的相關控制數已經有了很多結論.2001年,Proffitt等[1]確定了γp(Pn×Pm)的值,其中m=2,3;由Gravier[2]關于全控制數的結論可以得到γp(Pn×P4)的確定值;2008年,Bre?ar等[3]確定了γp(Cn×C4)的值,其中n≥3;2014年,文獻[4]確定了γp(Cn×Cm)的值,其中n≥3,m=3,4;2013年,裴利丹等[5]確定了γ(Pn×Cm)的值,其中m=3,4.本文主要討論笛卡爾乘積圖Pn×Cm(m=3,4)的配對控制數.

首先給出幾個記號及引理.分別用Cn和Pn表示階為n(n≥2)的圈和路,且將Cn,Pn的點標記為0,1,…,n-1.記Pn×Cm為Pn與Cm的笛卡爾積,V(Pn×Cm)={(i,j) |i∈V(Pn),j∈V(Cm)};記Yi={(i,j) | 0≤j≤m-1},0≤i≤n-1,則Yi為Pn×Cm的列.令Hji=Yi∪Yi+1∪… ∪Yi+j-1,i+j≤n.

引理2[4]當n≥3時,

引理3當n≥3時,

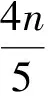
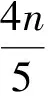
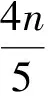
引理4當n≥5時,令D是Pn×C3的配對控制集,則|D∩H5i|≥4,0≤i≤n-5.

證明 設S=D∩H5i,其中H5i=Yi∪Yi+1∪… ∪Yi+4,0≤i≤n-5.令S1=D∩H3i+1,其中H3i+1=Yi+1∪Yi+2∪Yi+3.由D是配對控制集及圖的結構知,點集S控制子圖H3i+1.

1)D∩Yi+2=?.因為點集D中的一個點至多控制Yi+2中的一個點,且控制Yi+2的點都在Yi+1∪Yi+3中,又|Yi+2|=3,所以|S1|=|D∩H3i+1|≥3.由于D是Pn×C3的配對控制集,且與S1配對的點都在H5i中,所以|S|≥4.

2)D∩Yi+2≠?.因為D是Pn×C3的配對控制集,所以|S1|≥2.若|S1|≥3,則由上面的證明知|S|≥4.若|S1|=2,即S1是2個相鄰的點集,則圖H3i+1中2個相鄰的點至多控制H3i+1中的7個點.而|H3i+1|=9,故點集D在Yi∪Yi+4中至少有2個點控制H3i+1中沒有被S1控制的點.因此，|S|≥4.引理4證畢.

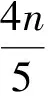
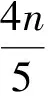
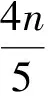
1)|D∩Y0|=0.因為D控制Y0中的點,故Y1?D.由D是配對控制集知,Y2中有一個點屬于D.因此，D∩I0?Y1∪Y2,從而Y3中有2個點不能被D∩I0控制.矛盾.

2)|D∩Y0|=3.由D是配對控制集知,Y1中有一個點屬于D.因此,D∩I0?Y0∪Y1,從而Y3中的點都不能被D∩I0控制.矛盾.

3)|D∩Y0|=2.因為D∩I0控制Y0∪Y1∪Y2∪Y3,所以|D∩(Y1∪Y2)|≥1.因此,|D∩Y3|≤1,D∩Y4=?.從而Y4中至少有2個點沒被D∩I0控制,所以|D∩Y5|≥2.若|D∩Y5|=3,則與2)類似可以得到矛盾.因此,|D∩Y5|= 2,從而Y9中至少有2個點沒被D∩I1控制.依此類推,Yn-1中有點沒被D控制.矛盾.

4)|D∩Y0|=1.因D是配對控制集,故|D∩Y1|≥1.若|D∩Y1|≥2,則D∩(Y3∪Y4)= ?.從而D∩I0不能控制Y4中的點.因此,Y5?D.從而與2)類似可以得到矛盾.若|D∩Y1|=1,則|D∩(Y2∪Y3)|=2.從而Y4中至少有一點沒被D∩I0控制,所以|D∩Y5|≥1.若|D∩Y5|≥2,則與2),3)類似可以得到矛盾.因此,|D∩Y5|=1,從而Y9中至少有一點沒被D∩I1控制.依此類推,Yn-1中至少有一點沒被D控制.矛盾.

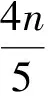
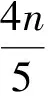
由γp(P1×C3)=γp(P2×C3)=2及引理3和引理5可得以下結論:

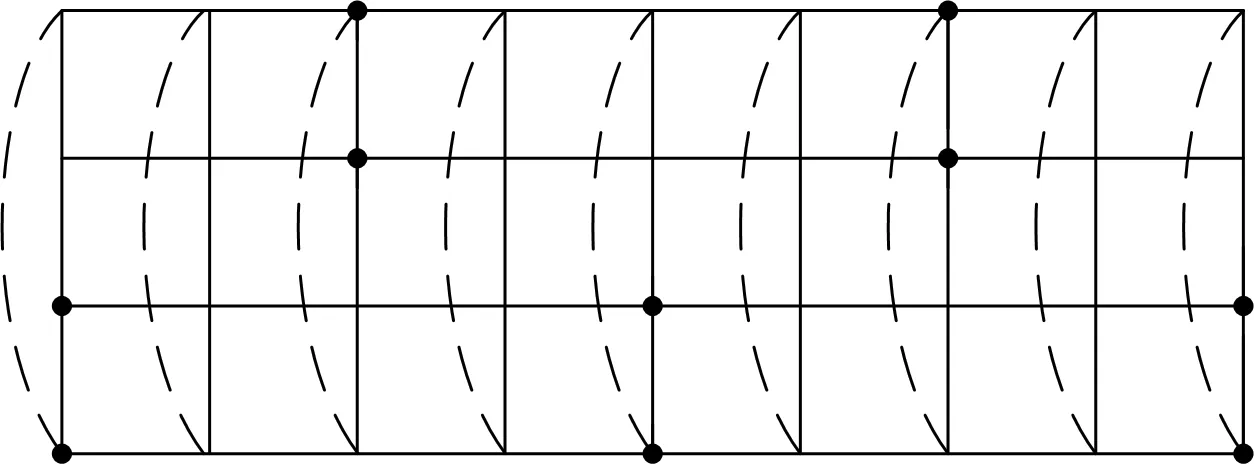
圖1 P9×C4的配對控制集(實點)

定理1當n≥1時,

引理6當n≥1且n≡1,3(mod 4)時,γp(Pn×C4)=n+1.

證明 當n≡1(mod 4)時,D={(i,0),(i,1),(i+2,2),(i+2,3):i≡0(mod 4),i≠n-1}∪{(n-1,0),(n-1,1)}是Pn×C4基數為n+1的配對控制集,如圖1所示.

當n≡3(mod 4)時,D={(i,0),(i,1),(i+2,2),(i+2,3):i≡0(mod 4)}是Pn×C4基數為n+1的配對控制集.因此,當n≡1,3(mod 4)時,γp(Pn×C4)≤n+1.

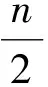
當n≡1,3(mod 4)時,γp(Pn×C4)≥n+1.因此,γp(Pn×C4)=n+1.引理6證畢.

引理7當n≥2且n≡0,2(mod 4)時,γp(Pn×C4)=n+2.

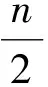
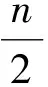
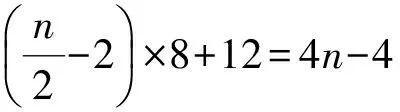
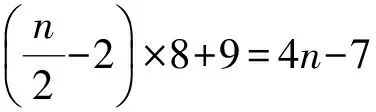
4)|D∩Y0|= 2.

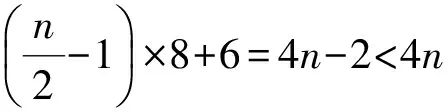
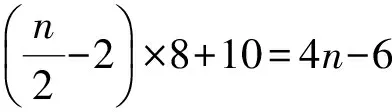
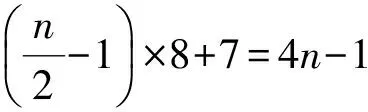
因此,γp(Pn×C4)>n.又因為配對控制數是偶數,所以γp(Pn×C4)≥n+2.

另一方面,當n≡0(mod 4)時,D={(i,0),(i,1),(i+2,2),(i+2,3):i≡0(mod 4)}∪{(n-1,0),(n-1,1)}是Pn×C4基數為n+2的配對控制集,當n≡2(mod 4)時,D={(i,0),(i,1),(i+2,2),(i+2,3):i≡0(mod 4),i≤n-3}∪{(n-2,0),(n-2,1),(n-1,0),(n-1,1)}是Pn×C4基數為n+2的配對控制集.因此,當n≡0,2(mod 4)時,γp(Pn×C4)≤n+2.引理7證畢.

由引理6和引理7可得以下結論:

定理2當n≥1時,

[1]Proffitt K E,Haynes T W,Slater P J.Paired-domination in grid graphs[J].Cong Numer,2001,150:161-172.

[2]Gravier S.Total domination number of grid graphs[J].Discrete Appl Math,2002,121(1):119-128.

[3]Bre?ar B,Henning M A,Rall D F.Rainbow domination in graphs[J].Taiwanese J Math,2008,12(1):213-225.

[4]Hu Futao,Xu Junming.Total and paired domination numbers of toroidal meshes[J].J Comb Optim,2014,27(2):369-378.

[5]裴利丹,連小娟,潘向峰.路與圈的笛卡爾乘積的控制數[J].合肥學院學報:自然科學版,2013,23(3):24-28.

(責任編輯 陶立方)

PaireddominationnumberoftheCartesianproductsofpathswithcycles

HUANG Haiyuan, MA Meijie

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

Based on the structure ofPn×Cmand the definition of paired domination number, by using the induction and contradiction method, it was determined the paired domination number of the Cartesian product ofPn×Cm(m=3,4).

Cartesian product graph; domination set; domination number; paired domination set; paired domination number

10.16218/j.issn.1001-5051.2015.02.008

2014-09-07

國家自然科學基金資助項目(11101378)

黃海圓(1990-),女,江西上饒人,碩士研究生.研究方向:圖論.

馬美杰.E-mail: mameij@zjnu.cn

O157.5

A

1001-5051(2015)02-0172-04