球式自動平衡裝置數值仿真系統設計

譚　青，任志湘，魏　來

（中南大學　機電工程學院，長沙410083）

球式自動平衡裝置數值仿真系統設計

譚青，任志湘，魏來

（中南大學機電工程學院，長沙410083）

在球式自動平衡裝置的數值仿真中，傳統的仿真方法是利用Matlab進行數值仿真，得到的結果不具直觀性和交互性。為了解決上述問題，現利用VB平臺，采用龍格—庫塔法對球式自動平衡裝置的數學模型進行數值求解，設計一種能夠使仿真結果動態可視化的交互式數值仿真系統。仿真結果表明，該數值仿真系統增加仿真結果的直觀性，實現滾球運動狀態的動態呈現。得到的仿真結果與自同期理論一致，不平衡轉子的振幅得到有效的衰減。

振動與波；球式自動平衡裝置；數學模型；數值仿真系統；減振

對于回轉機械而言，轉子不平衡將導致回轉機械產生振動和噪聲，甚至會引發災難性破壞，由此造成的損失不容忽視。目前，解決這一問題的一般方法是對其轉子進行高精度的動靜平衡［1］。由此，學術界展開了自動平衡課題的研究。球式自動平衡裝置是根據柔性轉子和彈性支撐的特性，不需要外部提供任何能量，只利用系統響應所形成的能量來驅動滾球的移動和分布，從而自動地消除轉子的不平衡。球式自動平衡裝置對于運動在過臨界轉速下的旋轉機械有較好的減振效益［2］。

以往研究中，借助數值分析方法求解球式自動平衡裝置運動微分方程的結果不夠直觀，并且無法直接觀察到其滾球的運動狀態及圓盤角速度和圓盤中心軌跡等。

根據球式自動平衡裝置的數學模型，借助Visual Basic 6.0平臺設計數值仿真系統，實現了球式自動平衡裝置仿真結果的動態可視化。考慮到在仿真過程中滾球會發生碰撞，將采用經過碰撞調整的適用于本數學模型的4階龍格—庫塔法求解。

1　球式自動平衡裝置的數學模型

球式自動平衡裝置的工作原理是轉子在過臨界轉速下旋轉時，轉子內滾球的位置將自動的受轉子機械振動相位的影響，移動到偏心質量的另一邊，一定程度上抵消偏心質量所產生的離心慣性力，從而起到減振的作用［2］。

球式自動平衡裝置的主要結構如圖1所示，一個轉盤固定在一根轉軸上，轉盤滾道內裝有若干滾球，其中轉盤中心位于O點，G處為不平衡質量，偏心距為e，滾球在半徑為R的滾道上運行，剛度和阻尼簡化到水平和豎直方向上。在建立數學模型時，將其結構簡化為轉盤和滾球兩部分，并做如下假設：

1）轉盤為均質圓形薄盤；

2）轉速視為按給定的函數變化；

3）球與滾道之間無相對滑動；

4）轉盤處在水平方向，不考慮軸向運動及重力影響。

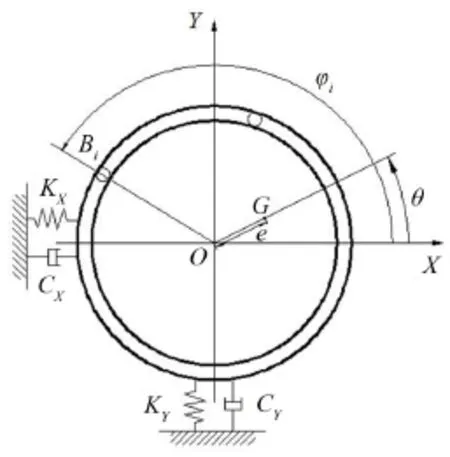
圖1　球式自動平衡裝置結構圖

所采用的符號表示如下（單位均采用國際標準單位）：

XOY：系統整體坐標系。以X和Y表示轉盤中心O的坐標。

Kx、KY：X方向的剛度系數和Y方向的剛度系數；CX、CY：X方向的粘性阻力系數和Y方向的粘性阻力系數。

θ：不平衡質量相對于X軸的轉角；

φi：第i個滾球的轉角。

β0：滾球的滾動摩擦系數；β1:滾球的粘性阻尼系數。

M：系統總質量，m1、m2、m3、m分別為偏心質量、轉盤質量、電機質量和滾球質量。

I、I1、I2：滾球的轉動慣量、偏心質量的轉動慣量、圓盤的轉動慣量。

R、r：滾球轉動半徑和球徑。

利用拉格朗日運動微分方程建立球式自動平衡裝置的數學模型，其推導過程參照文獻［3］第17至19頁，得到系統微分方程如下

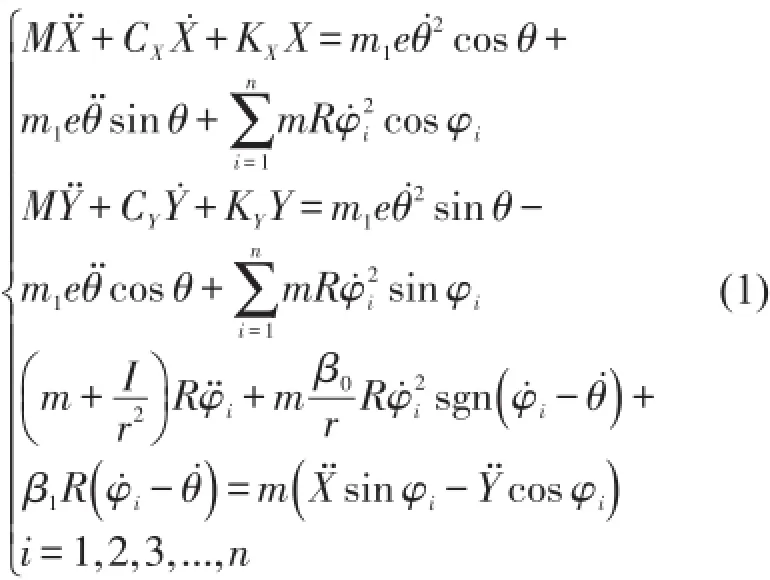
2　數值仿真系統的實現

采用四階龍格—庫塔法對上節給出的數學模型進行數值分析求解。數值分析需要借助編程平臺，對于一般的數學計算，首選Matlab，但Matlab在可視化上不如通用編程語言靈活，因此本文的計算將采用VB，利用VB強大的圖形化功能增加仿真結果的直觀性，實現滾球運動狀態的動態呈現。仿真程序流程如圖2所示。

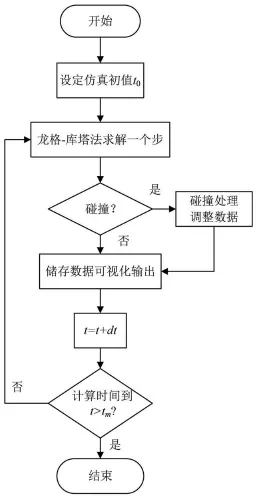
圖2　仿真程序流程圖

2.1系統微分方程化簡

將通用運動方程（1）化為便于仿真的通用格式1階微分方程組，以3球為例，取

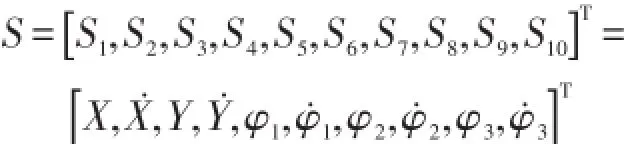
將定義的廣義坐標代入式（1）得到式（2），觀察可知，式（2）為已知初值的通用格式1階微分方程組，可以采用龍格—庫塔法求解。

2.2仿真參數

仿真參數依據實驗室原有的實驗設備確定，見表1。系統中仿真參數為變量，可通過改變仿真參數進行不同情況的仿真。

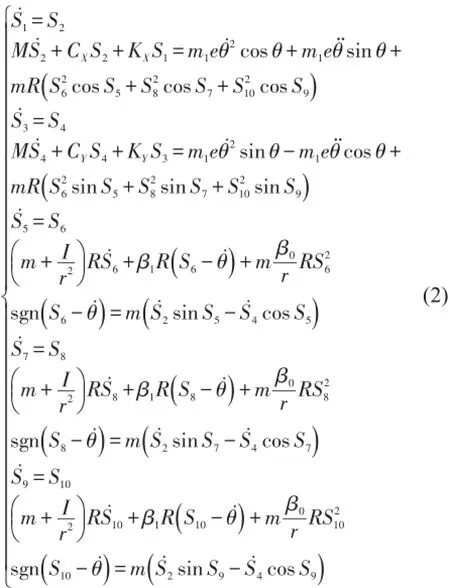
2.3仿真算法

仿真算法為4階龍格—庫塔法［4］。對于通用格式的1階微分方程組，如果初值可以確定，借助微機可以采用此算法求解。對于初值問題

4階龍格—庫塔法求解下一步的方法為

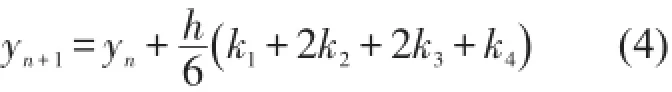
上式中h為步長，ki為

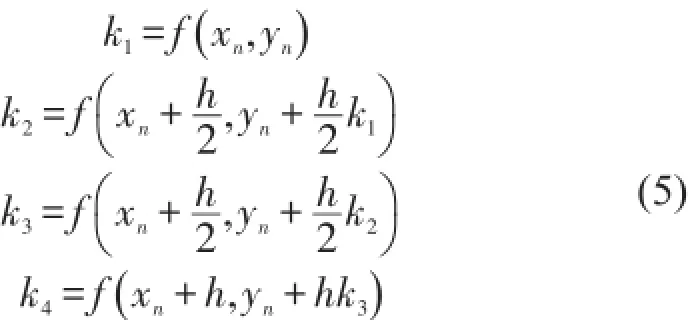
2.4碰撞調整

球式自動平衡裝置運動過程中的滾球可能會相撞，因此在龍格-庫塔法一個步的求解后，需檢查球的位置是否干涉，如果干涉須做碰撞處理。對于在滾道中運動的滾球，由于存在摩擦和粘性阻尼，可視為完全非彈性碰撞，即指滾球碰撞結束后，這一瞬間內兩物體的運動狀況完全相同，擁有相同的速度［5］。

兩球碰撞的判斷條件為兩球夾角φ滿足

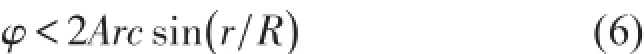
完全非彈性碰撞后的結果為兩球分別往各自兩側移動α

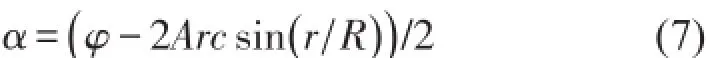
兩球速度均變為

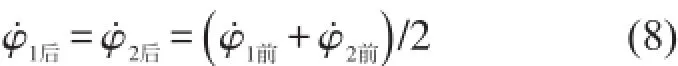
2.5數值仿真系統界面

基于VB設計的數值仿真系統主要輸出有X和Y方向的振幅、轉盤中心的運動軌跡、各滾球相對不平衡質量的轉角、滾球在轉盤內運動的動畫等。

該仿真系統具備計算0個滾球（視為不平衡轉子）和1～3個滾球（視為不同的球式自動平衡裝置）系統各項參數的能力。

軟件界面分三列，第一列四幅圖顯示振幅，分別為無滾球和有滾球情況下X和Y方向的振幅輸出，在無滾球計算完成后，保留振幅輸出圖像，便于同有滾球的時候形成振幅對比。中間列第一幅圖為角速度輸入，中間列后三幅圖為各滾球相對不平衡質量的轉角。最右邊列第一幅圖動態顯示滾球在轉盤內的運動情況，本模塊可以根據計算得到的轉角，以動畫的方式顯示滾球運動情況，不平衡質量在X軸正向，滾球以轉盤為參考系運行，最右邊列下面一幅顯示轉盤中心運動軌跡，也就是振幅在XY平面內的點云圖像。右下角的四個按鈕可以根據滾球數點擊，用來啟動仿真。

表1　仿真參數（未注單位為國際單位）

3　仿真系統的仿真結果

根據自同期理論［6］預測滾球在不同轉速下的位置：當轉速較低時，滾球向偏心質量一側移動，此時會造成轉子振幅增大；當轉速大于1階臨界轉速時，如果只是略大于，可能會產生自激振蕩，如果大得多，則滾球開始遠離偏心質量，達到平衡的目的［7］。下面分析四種不同滾球數目下的輸出，與自同期理論形成對比，驗證仿真系統結果的可信性。

殘留振幅是衡量過臨界轉速時移動物體對不平衡轉子減振能力的標志，最大振幅是決定轉子啟動時能否安全通過共振區的一項指標，因此最大振幅、殘留振幅作為評價自動平衡回轉機械工作機理影響因素的指標［3］。由于X、Y方向振幅規律相近，本文僅分析X方向振幅。

為了使仿真盡量接近實際情況，角速度輸入采用從0以5 s時間加速到25 Hz后勻速轉動。仿真時間持續30 s，每0.008 s取一個步，總共3 750個計算步。這里指出，仿真步的大小要選擇合適，步太大影響結果的準確性，步太小會導致仿真時間過長。

3.1不裝滾球

不裝滾球下的球式自動平衡裝置可視為普通不平衡轉子，其水平方向的振幅如圖3所示，從圖中的振幅走向可以看出，剛開始由于轉速不大，轉子振幅較小，之后轉子轉速達到一階臨界轉速后通過共振區，達到最大振幅，最后逐漸衰減為穩定值。最大振幅值和殘留振幅值可從圖上獲得（水平方向最大振幅由Xmax表示，殘留振幅由Xbal表示）。

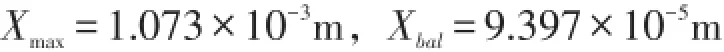
圖3　未裝滾球的計算結果

3.2 1個滾球

球式自動平衡裝置內裝有1個滾球的情況如圖4所示，滾球的原始位置相對不平衡質量的轉角為0，其X方向的振幅如圖4（a）所示。從圖中的振幅走向可以看出，剛開始由于轉速不大，轉子振幅較小，之后轉子轉速達到1階臨界轉速后通過共振區，達到最大振幅，該振幅超過了不裝滾球時的最大振幅，說明此時滾球加大了不平衡量，最后逐漸衰減為一個穩定值，該穩定值低于未裝滾球時的殘留振幅，說明滾球已經起到平衡不平衡質量的作用，符合自同期現象。圖4（b）顯示轉盤的中心運動軌跡。最大振幅值和殘留振幅值具體數值如下

Xmax=1.699×10-3m，Xbal=2.270×10-6m滾球最后相對不平衡質量的轉角為φ1'=-53.396 rad，化為角度，得滾球與不平衡質量最后的夾角為180.63°，接近理想角度180°。圖4（c）中的區域動態顯示滾球在轉過8圈后，緩慢移動到最后停留位置。

3.3 2個滾球

球式自動平衡裝置內裝有2個滾球，滾球初始轉角為0和π，基本情況同裝有1個滾球時相似，區別是兩個滾球可能會發生碰撞，上述初值下未發生碰撞，最大振幅同樣大于不裝滾球時的振幅。振幅穩定值低于未裝滾球時的振幅穩定值，減振效益十分明顯，說明滾球已經起到平衡不平衡質量的作用。最大振幅值和殘留振幅值及滾球停留位置具體數據如下

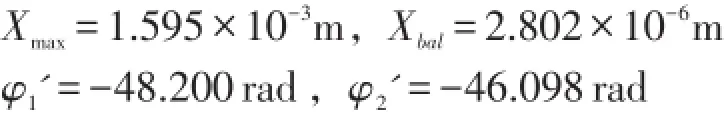
化為角度，得滾球1和滾球2與不平衡質量最后的夾角分別為118.34°和238.78°，分別接近理想角度120°和240°。球式自動平衡裝置裝有2個滾球的計算結果如圖5所示。

圖4　裝有1個滾球的計算結果

3.4 3個滾球

球式自動平衡裝置內裝有3個滾球的情況如圖

6所示，滾球初始轉角為0、2 π/3和4 π/3，其X方向的振幅如圖6（a）所示。從圖中的振幅走向可以看出，剛開始由于轉速不大，轉子振幅較小，之后轉子轉速達到1階臨界轉速后通過共振區，達到最大振幅，由于初始位置比較理想，該振幅略低于不裝滾球時的最大振幅，實際上此時滾球加大了不平衡量。最后逐漸衰減為穩定值，該穩定值低于未裝滾球時的殘留振幅，說明滾球已起到平衡不平衡質量的作用。這里指出在上述初始轉角下，滾球之間有相互碰撞。最大振幅值和殘留振幅值及滾球轉角具體數值如下

圖5　裝有2個滾球的計算結果

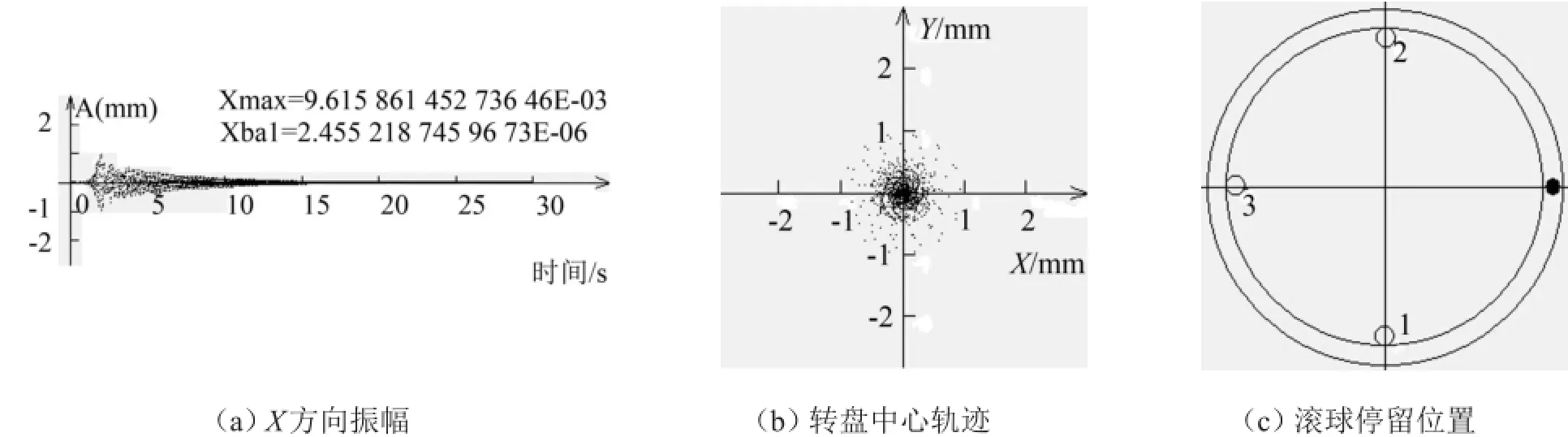
圖6　裝有3個滾球的計算結果

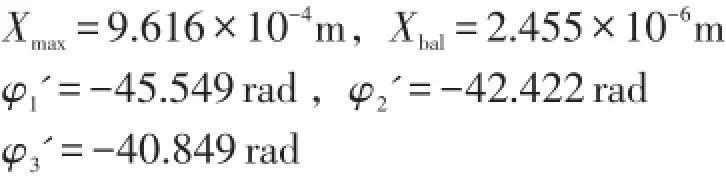
化為角度，得滾球1、滾球2和滾球3與不平衡質量最后夾角分別為270.23°、89.40°和179.52°，接近理想角度270°、90°和180°。圖6（c）顯示了滾球的最后停留位置。

4　結語

基于VB設計的球式自動平衡裝置數值仿真系統，通過參照（未裝滾球）和三組帶滾球的仿真，得到的仿真結果與自同期理論一致，不平衡轉子的振幅都得到了有效的衰減，減振效益達到40倍左右。

仿真過程中發現，減振速度與仿真步的大小有關，仿真步越小，滾球達到穩定位置的時間越長；殘留振幅與仿真時間有關，仿真時間越長，殘留振幅越小。

該數值仿真系統實現了球式自動平衡裝置仿真結果的動態可視化，增加仿真結果的直觀性，實現了滾球運動狀態的動態呈現。通過修改仿真系統的參數，可以很便捷的分析仿真結果的影響因素，包括初始位置、滾道摩擦系數、滾道阻尼系數、轉子旋轉加速度等。

［1］劉文倩，譚青，謝燕琴，等.自動平衡裝置減振效益分析［J］.噪聲與振動控制，2010，30（4）：153-157.

［2］譚青，周鐵，黃秀祥.球式自動平衡裝置的數值仿真與實驗研究［J］.噪聲與振動控制，2008，28（3）：142-145.

［3］周鐵.內裝滾球轉子自同期現象的理論與實驗研究［D］.長沙：中南大學，2008.

［4］Brooks Cole.馮煙利譯.數值分析［M］.北京：高等教育出版社，2005.

［5］哈爾濱工業大學理論力學教研室.理論力學（第七版）［M］.北京：高等教育出版社，2010.

［6］井上順吉，荒木嘉昭.振動機械的自己同期化研究（日文）［C］.日本機械學會論文集，1967，33（2）.246.

［7］楊義蛟，譚青，周鐵.自動平衡回轉機械的工作機理研究［J］.機械設計與研究，2009，（4）：33-36.

Design of Numerical Simulation System of Ball-type Automatic Balancers

TANQing，REN Zhi-xiang，WEILai
（College of Mechanical&Electrical Engineering，Central South University，Changsha 410083，China）

The Matlab code is used very often in numerical simulation of ball-type automatic balancers.But the results are neither intuitive nor interactive.In this paper，a new dynamic simulation system with VB platform was designed.The mathematical model of the ball-type automatic balancers was solved numerically using Runge-Kutta method.The simulation results show that the system enables interactive visualization and intuition of the simulation results and realizes the dynamic presentation of the state of dynamic motion of the balls.The simulation results obtained by the numerical simulation system of the ball-type automatic balancers are consistent with those of the self-synchronization theory.The amplitude of the unbalanced rotor is reduced effectively.

vibration and wave；ball-type automatic balancer；mathematical model；numerical simulation system；vibration reduction

TP311；TH113.1

ADOI編碼：10.3969/j.issn.1006-1335.2015.05.009

1006-1355（2015）05-0048-05

2015－02－12

任志湘（1990－），女，湖南省岳陽市人，碩士生，主要研究方向：自動平衡裝置虛擬實驗平臺。

Email：jds-share@163.com

譚青（1955－），男，博士生導師。