運算律，無論在哪里都適用嗎？

顧巍偉 嚴育洪

“望”：病例觀察

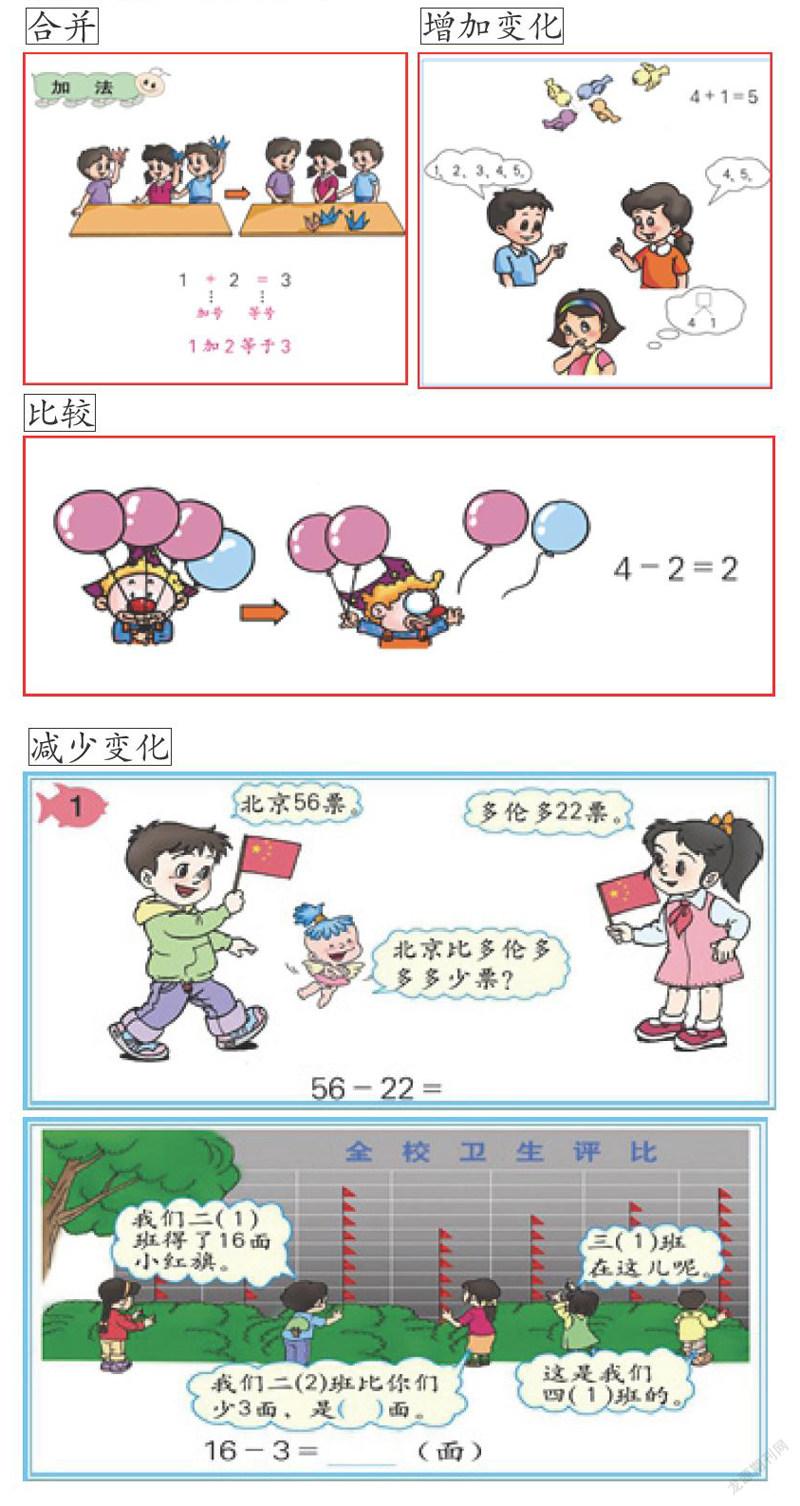
【片段1】一位教師在教學“加法交換律”和“加法結合律”之后，出了這樣一道選擇題：25+38+75=25+75+38，這里運用了（ ）。A.加法交換律；B.加法結合律；C.加法交換律和加法結合律。許多學生選擇A。揭示答案是C后，教師在學生的辯駁“只是38和75交換了位置啊”中，也說不出所以然來。

教師最后總結說：“兩個數相加可以交換位置，三個數相加也可以改變運算順序。你們還有什么想法嗎？”

生：無論多少個數相加，都可以改變運算順序，和都不會變。

師：對，是這樣。你真棒！

……

【片段2】一位教師教學“加法交換律”，課始組織了兩位學生交換位置、兩件物品交換位置等活動，然后由此導入新課：“在數學中，也有著類似的交換現象。這節課我們就一起來研究。”

……

課終，教師播放了《朝三暮四》的flash動畫：“在這個故事中，你能找到加法交換律嗎？”

當學生找出“3+4=4+3”后，教師總結道：“確實，‘朝三暮四’和‘朝四暮三’結果是一樣的，因為它符合加法交換律。”教師接著又補了一句：“看來，加法交換律不僅在數學中普遍適用，而且在生活中也普遍適用。”

……

“問”：病歷記錄

對于片段1的教學，筆者在課后對執教教師進行了如下訪談。

筆者：你是怎樣判斷交換律和結合律的？

執教者：交換律改變的是數的位置，結合律改變的是數的運算順序。25+38+75=25+75+38，我感覺只是改變了38和75的位置，并沒有改變從左往右依次運算的順序啊！（說完，一臉困惑，這也是她沒在課內表態的原因——對標準答案心存疑惑）

筆者：對于“無論多少個數相加”，你是怎么理解的？

執教者：我認為既可以有限個數相加，也可以無數個數相加，對嗎？

筆者（點頭）：那無數個數相加，加法交換律和結合律還適用嗎？

執教者（一臉疑惑）：難道不可以嗎？

……

對于片段2的教學，筆者也對執教教師進行了一次訪談，具體如下。

筆者：對于“加法交換律在數學中普遍適用”這句話，你覺得有問題嗎？（執教者對這一問題感到驚訝和不解）

筆者：那后半句“加法交換律在生活中也普遍適用”，你覺得有問題嗎？

執教者（不再猶豫）：沒問題啊，數學源于生活，例如生活中有著許多像兩個人交換位置、兩件物品交換位置等交換現象，基于這樣的考慮，所以我設計了從生活中的交換現象引入數學中的交換現象的教學環節，學生一下子就理解了。

……

“切”：病理診治

運算律，顧名思義，數運算中的規律。基本運算律以及初中階段將要學習的指數運算法則，被統稱為“數與代數”領域的“通性通法”。運算律是小學數學中唯一以定律方式呈現的內容。

片段1中，執教教師所說的“交換律改變的是數的位置，結合律改變的是數的運算順序”，僅僅關注了數的位置和數的運算順序，忽視了另外一個重要的前件。例如加法交換律“如果兩個數相加，交換加數的位置，那么和不變”（許多教材和教師在表述時，為了讓語句簡短，常常省略“如果……那么……”這一關聯詞語，甚至把“兩個數相加”也省略了，最終剩下“交換加數位置，和不變”），具有“若P則Q”假言命題的形式，P稱為命題的前件，Q稱為命題的后件，前件和后件構成了命題的整體。

實際上，數學中的“交換律”是指：一種運算“*”和參加運算的某集合A中的任意“兩個元素”a、b，一定有a*b= b*a，我們就說運算“*”對于集合A滿足交換律。由此可見，“兩個元素參加運算”這一前件忽視不得，否則在判斷“25+38+75=25+75+38”究竟用了什么運算律時就會發生知識性錯誤。

具體來看，“25+38+75=25+75+38”已經是三個數連加，按照運算規則，在“25+38+75”中，38只與25運算，其和63才與75運算，怎么可以運用加法交換律交換38和75的位置呢？也就是說，正是因為加法還滿足結合律，才能將38和75的位置交換過來，它可以看成是加法交換律和加法結合律的綜合應用（如下圖）：

加法結合律如果聯系加法交換律，那么加法結合律可以進一步延伸：三個數相加，可以把任意兩個數先相加，再加上第三個數，和不變。甚至可以推廣到更多的數相加的情況，經過加法交換律和結合律的多次綜合運用，得到“多個數相加，都可以改變運算順序，和不變”。從表面上看，多個數相加可以任意交換位置，似乎只是運用了交換律，其實應該說多個加數的基點最終是通過結合律化歸到兩數交換律。只是在實際操作中，人們對“交換”這一特征印象更清晰，直接導致“只運用了交換律”的誤見。

我們可以把“a+b+c = a+c+b”這樣一個規律說成是由加法結合律和交換律證明了的一個“推論”。嚴格地說，“a+b+c = a+c+b”應用的運算律不是加法交換律的推廣而是加法交換律和結合律的推廣。對乘法也是如此，可以合并表述為：三個以上的數相加（乘），任意交換加（乘）數的位置，或者先把其中的任意幾個結合成一組相加（乘），再同其他數相加（乘），它們的和（積）不變。

由此，我們還可以看出，加法交換律和結合律通常在加、減運算中同時使用，交換的目的在于結合，結合時一般是按正負結合，按相反數結合，總之，將容易計算的數進行結合；乘法交換律和結合律通常在乘、除運算中使用，交換的目的同樣是為了結合，結合時一般是將能約分的數結合。

五個基本運算定律適用于小數、分數、有理數、實數、復數，在中小學數學學習中通行無阻。那么，是否像片段2中執教教師所說的“（加法）交換律不僅在數學中普遍適用”呢？答案是否定的。

首先，運算律只能運用于有限集合的運算，而不能運用到無限集合中。例如：

算法一：1-1+1-1+1-1+…=1+（-1+1）+（-1+1）+…=1或1-1+1-1+1-1+…=1-（1-1）-（1-1）-…=1；

算法二：1-1+1-1+1-1+…=（1-1）+（1-l）+（1-1）+…=0。

同一道題得出兩個不同的答案，當然是不允許的，其原因就是在無限范圍內使用了加法交換律和加法結合律。由此可見，片段1中學生的發現——“無論多少個數相加，都可以改變運算順序，和都不會變”，這種說法不對。

其次，學習了高等代數，就會知道代數運算不一定具有交換或結合的性質。例如，n次置換的乘法能滿足結合律，但不滿足交換律；n階矩陣的乘法不滿足交換律，但滿足結合律。

再次，對定義新運算，例如，對于運算，交換律和結合律都是不適用的。

綜合以上知識，我們就能得到這樣一個結論：運算律在數學中并非普遍適用。那么，運算律在生活中是否也普遍適用呢？答案也是否定的。

片段2中，執教教師課始采用兩位學生交換位置、兩件物品交換位置導入新課，作為引子可以，不過還是有著本質的區別。執教教師說的“數學源于生活”，只對了一半，完整的說法應該是“數學源于生活但高于生活”，也就是說“數學不完全等于生活”，以本節課而言，運算律不能濫用于生活，萬事萬物在發展順序和運作順序上往往不滿足“交換律”，例如穿衣服，先穿內衣再穿外衣，你就不能交換過來，先穿外衣再穿內衣，時間也是無法“交換”，你先上樓再下樓，有可能與先下樓再上樓的結果不一致。

綜上所述，執教教師最后的補充——“看來，加法交換律不僅在數學中普遍適用，而且在生活中也普遍適用”并沒有起畫龍點睛的作用，反而成了畫蛇添足，是教學的敗筆。

我們再來看教師說的前一句話——“‘朝三暮四’和‘朝四暮三’結果是一樣的”，如果脫離情境，純粹地看數學等式“3+4=4+3”，毫無疑問它符合加法交換律，但如果放到生活中就未必符合加法交換律，例如從養生角度看，“早上吃得少晚上吃得多”與“早上吃得多晚上吃得少”對健康的影響未必一樣；從創新角度看，“從‘三’追求‘四’”與“從‘四’追求‘三’”顯示的精神狀態未必一樣；從經濟角度看，“先拿到‘三’”與“先拿到‘四’”所產生的經濟效用未必一樣……

綜上所述，運算律在數學中并非無論在哪里都適用，在生活中也并非無論在哪里都適用，所以教師需要三思而后言。

（江蘇省無錫市張涇實驗小學 214194

江蘇省無錫市錫山教師進修學校 214191）