基于預習的“問題誘導”教學

過曉偉

培養思維能力是由“問題”開始的，又是在問題解決中發展的，這也是學好數學的前提。學生在課前預習中產生的疑問往往是其與新知對話的結果，它實際上可以為學生走進課堂提供良好的學習準備，基于預習狀態下的“問題誘導”教學，抓住學生在預習中產生的問題進行設計，并通過和諧的互動誘發學生持續思考，促使他們去發現新知、探索新知，進而提高數學思維能力。下面筆者以蘇教版三年級上冊“兩、三位數除以一位數”的教學為例，來談一些具體的做法和思考。

一、匯聚“預習疑問”，設計“核心問題”，明確學習方向

學生通過預習，會在疑難處和新舊知識點鏈接矛盾的地方產生問題，如每個同學提一個問題，全班就會匯聚一串問題，這些問題有的細小、零碎，有的籠統，也有的具有思考性、啟發性。這些問題來自于學生認知上的不同理解，課上一一解答顯然效率低下，而且重點不突出。由此課堂上應對問題加以甄別，進行分類整合，進而形成直指本質、涵蓋教學重難點、具有高水平的、以探究為主的“核心問題”，這樣，這些具有思考性、探究性的問題就能讓學生迅速明確學習目標，為學習思考指明方向。

例如，在教學蘇教版三年級上冊“兩、三位數除以一位數”時，筆者對學生的問題作了如下整理：

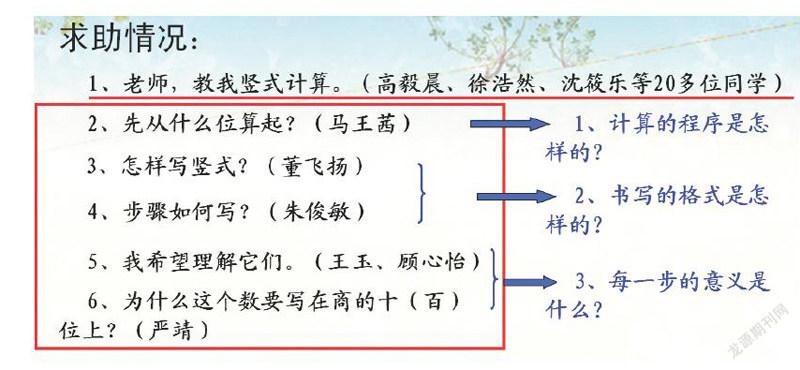
學生的問題一般具有共性，第一個問題有多位學生提出，其實是一個學習需求的集中求助，其他幾個提問則目的性非常強，但在教學中不可能分裂開來解決，于是筆者把它們進行分類整合，歸納成三個學習的“重點問題”，以這三個“研究問題”貫穿全課。這三個問題其實就是新課內容的核心，抓住這三個問題，學生也就明確了新知的重點，解決了難點。因此，課堂上把學生的疑問采用化繁為簡的策略進行歸納整理，變“問題串”為“大問題”，變“多環節”為“大板塊”，改變原先教師一步一臺階、降低思維難度的一串串小問題的“點狀思維”教學方式，讓學生自主探究“核心問題”，這樣充分凸顯了以學生為主體的學習方式，也給學生創設更多時空去探索、去思考，有利于培養良好的思維品質。

二、基于“初步認識”，設計“啟發性問題”，啟迪積極思維

通過預習，學生對新知會有一定的認識，但在知識重構中會出現模糊、混淆、不全面、不規范的現象。在教學實踐中，教師不能代替學生學習，不能簡單地教給學生一個結論，而在于引導學生通過自己的思維活動掌握獲取知識的過程和方法。因此，教師要根據新舊知識的內在聯系，精心設計“啟發性”的問題，啟發學生通過自己的積極思維主動地尋找答案。

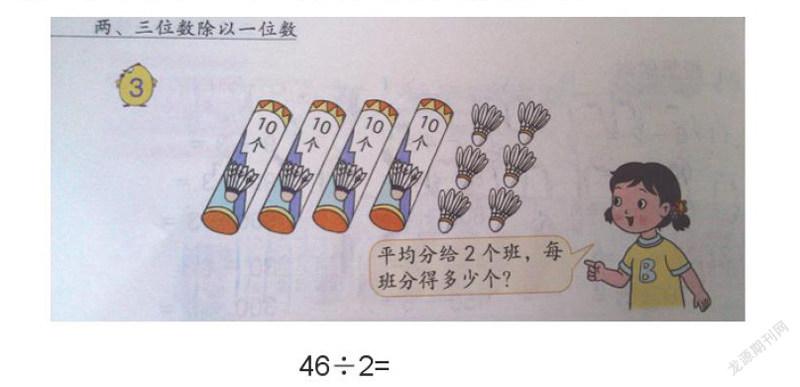
例如，在教學蘇教版三年級上冊“兩、三位數除以一位數”時，筆者出示以下情境圖：

學生列式后，設計了如下問題：“你想怎么算呢？能用畫圖、文字或算式說明嗎？”

學生通過自主思考，呈現了如下多樣算法：

上面通過“你想怎么算”這個綜合性的問題，讓學生自主思考“分”與“算”的過程。由于學生會分而不會算，所以學生就根據“問題”中的提醒“可以通過……”來解決“46÷2=”的問題，以上算法雖然只展現了分的過程，但其實已經展現了學生由“圖—文字—式”思維的數學化過程。隨后，筆者又提出以下幾個問題：“這么多的分法其實都是先分什么，再分什么？”“都是先算什么，再算什么？”“哪種方法你覺得既簡潔又包含了全部分的過程，為什么？”這些帶有“啟發性”的問題讓學生對眾多分法有了更深入的了解，對豎式計算的算理有了新的認識，為豎式計算的學習做好了準備。以上的教學展示、分享環節，不是簡單的“說一說，看一看”，而是在學生展示自己原始思維的同時，通過闡述、分析、比較、篩選等智力活動，圍繞多種原始思維展開的深度對話，完善和提高了個體認識。

所以，課堂中教師要在“關鍵處”善于設計啟發學生思考的問題，準確把握學習的方向，讓學生在初步認識的基礎上得到充分交流經驗、探討、剖析的機會，讓學習不斷深入。

三、依據“學習經驗”，引領“關鍵問題”，拓展思維深度

數學知識比較抽象，要讓學生真正理解和自覺掌握數學基礎知識并形成能力，關鍵在于對所學內容的深度理解。學生通過預習，對所學內容會有一定的了解，但在“關鍵問題”上還需要教師的引領，所以教師要盡可能地利用有限的時間，通過對“關鍵問題”進行廣泛、深入的剖析，由淺入深，使學生對教學內容達到深度的理解。

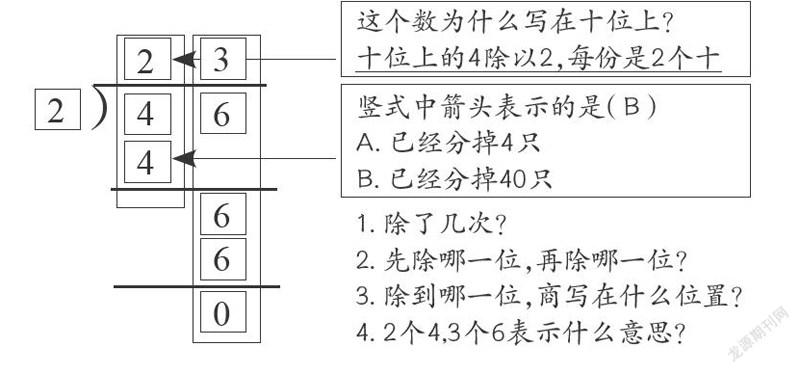
例如，教學蘇教版三年級上冊“兩、三位數除以一位數”時，筆者設計了如下一些問題：

以上的教學通過不斷地追問，不僅讓學生懂得如何計算，而且是對每一步、每一個數都進行了辨析，明晰了算法，理解了算理。在此基礎上，筆者繼續深入，又提出：“除法豎式與以往的其他豎式有什么不同點？”讓學生對比不同的豎式，最后歸納總結出：

1.其他豎式都是把要計算的數上下對齊排列，除法豎式是把除數和被除數寫在同一行。

2.其他豎式都是把要計算的數寫在上面，結果寫在下面，除法豎式是把結果寫在最上面。

3.其他豎式都是從右向左計算，即按照個位數、百位數、千位數等由小算到大，除法豎式卻是由最高位算起。

通過對以上“關鍵問題”的積極討論和充分說理，學生對除法豎式有了更深刻的理解，不僅從模仿或單純的計算中解脫出來，而且學生的思考得到了檢查、強化、驗證，零散的思考變得系統化、結構化，停留在表面的思考通過解釋說明、質疑問難得到了深化，學習逐步走向深入，“數學理解”思想得到體現。

基于預習狀態下的“問題誘導”教學在于要關注學生的已有認知水平和學習經驗，充分尊重學生的原創思維，在匯聚眾多疑問的基礎上的“重要問題”“核心問題”“關鍵問題”是學生學習的關鍵，課堂上以“問題導思”為目標，為學生創設了更多的時空，讓他們有時間和空間去自主探索、動手實踐，這樣，學生的思維會更主動、更靈活、更廣闊、更深刻，學生的良好思維品質也得到了培養。

（江蘇省無錫市云林實驗小學 214101）