幾何畫板在中職數學教學中的應用和作用

廖宗明

摘 要： 在現今的中職數學教學中，幾何畫板以它強大的功能改進了中職數學的教學手段。本文對幾何畫板功能進行了分析，用實例概括了幾何畫板在中職數學的一般應用，研究了幾何畫板對中職數學教學所起的作用。結論表明，合理利用幾何畫板教學，能夠提高中職課堂數學學習效率。

關鍵詞： 中職數學教學 幾何畫板 教學應用 教學作用

在知識經濟時代、信息社會中，知識以人們無法想象的速度在增加和更新，中職數學教學手段、教學方法也在不斷改進，從以前的黑板上教學逐漸過渡到現在的多媒體輔助教學。前蘇聯著名數學家A.H.柯爾莫戈洛夫指出：“只要有可能，數學家總是盡力把他們正在研究的問題從幾何上視覺化。”

幾何畫板是一個通用的數學教學環境，提供豐富而方便的創造功能，使用戶可以隨心所欲地編寫出自己需要的教學課件。相對于PowerPoint、Flash等中職數學教學輔助軟件，幾何畫板在中職數學圖形的空間結構、軌跡的形成等方面，有著不可取代的優勢。它并非只是替代了直尺、圓規的一個畫圖工具，更重要的是它所作的圖形、圖像是動態的，更注重中職數學表達的準確性，其最突出的優點就是使圖形、圖像在運動的狀態下保持不變的幾何關系。由于幾何畫板學習入門容易，操作簡單，資源節省，以及其強大的動畫功能等優點，已被越來越多中職數學教師所重視，它必將給中職數學教學帶來不小的變革。

一、幾何畫板的功能

幾何畫板以點、線、圓為基本元素，通過這些元素的構造、變換、平移、旋轉、縮放、反射等可以構造復雜的圖形。在中職數學教學中，幾何畫板為新的探索式教學提供了可能。它有以下幾個功能。

1.圖形繪制及度量、計算功能幾何畫板中，不僅有直角坐標系功能，還能畫出解析。

幾何中所有的二次曲線，還有極坐標系，可以作出由極坐標確定的所有曲線。在同個坐標系中，可以作出多個函數圖形進行比較，利用圖像的直觀性，給學生創造觀察、比較的環境。比如：可以利用幾何畫板畫出指數函數的圖像；利用幾何畫板度量直線傾斜角的角度；利用幾何畫板度量任意兩點間的距離。

2.圖形變換功能。

幾何畫板提供了平移、旋轉、縮放、反射等圖形變換功能，可以按指定的值或動態的值對圖形進行這些變換。只要給出函數表達式，就可以做出任意一個給定區間上的初等函數圖像，并且可以動態控制含若干個參數的函數圖像，隨著參數值的變化，圖像的形狀也跟著變動。比如：可以作出函數y=ax■+bx+c的圖像，并可以改變參數a、b、c的大小，進而改變圖像的形狀。

3.對幾何定理的展示。

如果存在不變的幾何關系，即幾何定理，幾何畫板就能使這些幾何關系保持不變。比如：可以利用幾何畫板證明和展示角平分線定理。

4.動態對象的跟蹤。

幾何畫板能對動態對象進行跟蹤，并能顯示該對象的軌跡，如：點的軌跡、線的軌跡、形成曲線等。比如：我們要求到線段兩端距離相等的點的軌跡，就可以利用幾何畫板動態地把點的軌跡顯示出來。

5.簡便的動畫功能。

幾何畫板可以針對幾何教學的要求制作動畫和移動對象，可以體現幾何體的運動。比如：可以利用幾何畫板進行三角形翻折、繞某點旋轉。

二、幾何畫板在中職數學教學中的應用

1.繪制精確的幾何圖形。

規范準確的幾何圖形往往能給人以美的享受。作為中職數學教育工作者，我們應該充分認識這一點，并要善于運用這個特點輔助我們的教學。幾何畫板這個軟件正好給我們提供了這樣的一個平臺，它不僅可以準確地繪制出任意的幾何圖形，而且可以在運動過程中動態地保持元素之間的幾何關系。

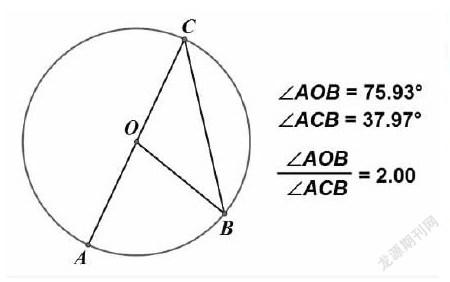
例如：中職數學里面的圓周角定理，在常規的教學中，往往是先由教師給出定理，再證明定理，最后舉例應用。這樣處理教材的內容往往使定理失去了應有的魅力，難以激發學生學習中職數學的熱情和興趣。再者，很多中職學校缺少教具，利用隨手畫的圓教學，圖形不美觀，教學效果不好，也缺少了中職數學的圖形美。如果在教學中能把幾何畫板引入課堂，并制作成相應的課件，不僅體現了中職數學圖形美和圖形幾何的嚴謹性，還能動態地研究定理的結論。比如下圖：利用幾何畫板的拖拉、測算等功能，可以任意地拖動A、B兩點以改變該A、B、C三點的位置，讓同學們觀察相應圓周角和圓心角的大小和它們的比例關系，并試著用自己的語言進行歸納總結，進而提出圓周角定理。有條件的話，可以讓學生自己動手親自試驗；在同學們觀察實驗的基礎上，教師再利用構造圖形的方法對該定理給予證明。這樣讓學生通過老師或自己的操作感受其中的規律，體會其中的艱苦，嘗試成功后的喜悅，從而培養他們學習幾何的興趣。

2.研究函數的圖像及性質。

中職數學里面有冪函數、指數函數、對數函數、三角函數，函數的圖像和性質在中職數學里既是重點又是難點。如果在教學中能充分利用幾何畫板將抽象的內容具體化、形象化，那么對于學生的學習無疑是很有幫助的。

例如：教學中職數學里面的指數函數時，為了更好地研究函數的圖像和性質，可以借助幾何畫板做演示。通過移動P點改變指數函數底數a的大小，讓學生通過觀察或操作理解底數a的大小改變對指數單調性的影響；在移動動點P的過程中觀察B點的坐標一直不變，得出指數函數都經過點（0，1）；移動點P并移動點A，觀察點A的坐標，得出指數的定義域是實數集，值域是正實數集。

這樣，就會使整個內容變得非常形象直觀，易于接受，比過去直接用理論說明或簡單地在黑板上畫幾個草圖講解的效果要好得多。在學習其他的函數圖像和性質時，也可以采取類似的方法，從而使中職數學的課堂變得豐富多彩。

3.探尋點的軌跡。

中職數學里面的直線的方程、圓的方程、拋物線的方程和雙曲線的方程，都是點的軌跡的問題，一直以來都是學生比較難以理解和掌握的問題，大多中職數學生只能在頭腦中簡單地想象或手工地畫出其草圖，而這樣不能保證所畫圖像的精確性，尤其是對初學者來說，更難以形成自己的知識，達到熟練應用的程度。如果應用幾何畫板，就可以動態地描繪出軌跡的形成過程，使學生能夠更容易地抓住其本質進行學習。

例如：在學習橢圓這一部分內容時，可以利用幾何畫板演示利用橢圓的定義作橢圓。簡要步驟：

（1）作點A、B，以及線段CD（定長）；

（2）以點A為圓心，CD為半徑作圓，并在圓A上任意取一點E；

（3）連接AE、BE，并作BE的垂直平分線FG，交BE于點F，交AE于點G；

（4）同時選中點G和點E，作軌跡，如圖：

在教學過程中，我們不妨在課堂上一步一步地直接給出該課件的制作過程。通過對這個過程的了解，學生可以非常容易地知道點G就是到定點A、B等于定長的點。當點E在圓上不停地運動時，點G的軌跡正好就是橢圓。于是橢圓的形成過程就完全地展現在學生的面前，這對于他們的形象記憶是很有好處的。當然，為了更好地說明問題，還測算出AG及AG和BG的長度之和，這樣可以使學生非常方便地觀察出動點G在運動過程中其他的量與量之間的關系，從而對橢圓的形成過程有進一步認識。

在幾何畫板中，橢圓的做法有很多種，我們可以鼓勵學生在課下自己動手，試著用其他的方法作出橢圓，以達到舉一反三的目的。這樣在接下來學習雙曲線這一部內容的時候，就可以讓同學們自己動手探索問題了。不僅是圓錐曲線這一部分的內容可以用幾何畫板輔助教學，其他很多有關點的軌跡的問題也都可以由它幫助解決。

4.探索直線和直線的關系、直線和圓的位置關系。

直線和直線的關系、直線和圓的位置關系，用幾何畫板教學比較直觀，容易理解，且具有說服力。

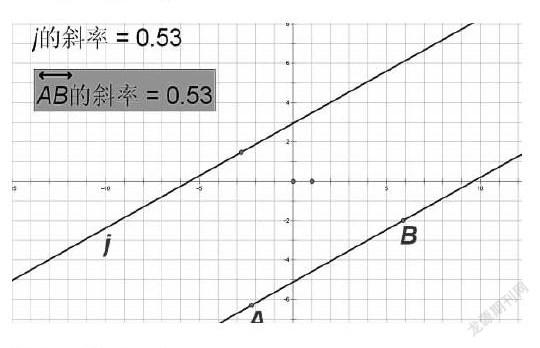
如圖，拖動兩條直線，隨意改變兩條直線的位置，觀察到，兩條直線的斜率相等。因為作圖比較簡單，可以引導學生自己作圖，自己操作測量，最后驗證兩條直線平行的充要條件：斜率相等。

三、幾何畫板在中職數學教學中的作用

1.創設情境，幫助理解中職數學概念。

很多中職數學概念十分抽象，學生不太能理解，通過有聯系的引入，讓學生了解概念提出的背景，才能讓學生深入理解中職數學。

比如：斜率的教學，利用幾何畫板可能動態地演示斜率變化，引起的直線的傾斜程度的變化，讓學生更深刻地理解斜率這個概念。

2.動態演示，顯示軌跡，突破教學難點。

一直以來，中職數學教學就強調邏輯性，但不太考慮學生的空間想象力。在學習圓柱等幾何圖形時，只能看到簡單的幾個實物和并不復雜的圖形，卻沒有深入了解幾何圖形。幾何畫板的出現，簡化了教師教導幾何這方面的問題。在幾何畫板里，學生可以動態地觀察、探索，根據圖像的運動，發現對象間的變化關系。

3.體現數形結合的中職數學思想。

數形結合是學習中職數學的重要方法，用圖形解釋抽象的中職數學現象形象、直觀。通過觀察幾何畫板里的圖像，可以把抽象變為形象，微觀中職數學轉化為宏觀中職數學。比如：曲線的方程的教學，用幾何畫板動態動演示曲線的變化會引起方程的參數變化，方程的參數的變化同樣也引起曲線形狀的變化。

4.開展中職數學實驗，進行研究性學習。

獲得中職數學知識的過程，離不開反復的實驗與觀察，對實驗觀察資料的思考：歸納、類比、聯想、猜想……單憑邏輯推理是發現不了中職數學的。幾何畫板顯示出了超凡的威力，幾何畫板改變了中職數學教學方式，使得許多應用中職數學問題一下子直觀起來。比如：講授兩條直線的平行和垂直的條件時，讓學生利用幾何畫板操作發現兩條直線平行和垂直與這兩條直線斜率之間的關系。學生通過自己的實驗發現和驗證了兩條直線平行和垂直的條件。以幾何畫板為工具，讓學生動手實踐，親自操作經歷了知識的生成和知識的構建過程，這樣知識必然是深刻的、牢固的。幾何畫板所創造的學習過程的快捷，形象、生動性必然會給學生留下極為深刻的印象，進一步增強學習的積極性和求知欲望。

總之，幾何畫板在中職數學課堂教學中的廣泛應用和推廣，不僅帶來了教學內容、教學方法、教學模式的深刻變革，而且使學生接受知識的被動地位得以改變，真正體現課堂教學中學生的主體地位和教師的主導地位，對提高學生中職數學素質和教師的教學能力有著重要作用，同時對我國的素質教育起著重要的推進作用，為國家培養出大量高素質的綜合型人才。

參考文獻：

[1]蘇強.基于幾何畫板的數值計算課件開發研究[J].宜春學院學報，2012（12）.

[2]李瓊.簡談《幾何畫板》在高中數學教學中的應用[J].山西師范大學學報（自然科學版），2011（S1）.

[3]徐新愛，胡啟宙.用幾何畫板研究二次函數性質[J].教學月刊（中學版），2011（01）.

[4]應茜.利用幾何畫板輔助初中函數教學的實踐與研究[D].蘇州大學，2010.

[5]李紅莉.應用幾何畫板輔助物理教學的研究[D].湖南師范大學，2005.

[6]陶丹.幾何畫板在圓錐曲線中的應用研究[D].江西師范大學，2005.