“方程像什么”，這樣的舉例合適嗎？

顧利國　嚴育洪

【“望”：病例觀察】

在一節“認識方程”的課中，教師設計了以下幾個教學環節：一是以天平為載體呈現等量關系和不等量關系，然后進行分類得到方程；二是以方程的定義為切入點，從“等式”和“未知數”兩個要點認識方程，并通過大量練習進行強化，最終學生都能抓住教師再三強調的“等式”和“未知數”兩個要點來判斷是否方程。

在課即將結束的時候，教師讓學生回顧對方程的認識，開始回答的學生都在復述方程的意義——“含有未知數的等式叫作方程”。教師正在進行全課總結，有一位學生談了自己的學習體會：“我覺得方程就像兩個雙胞胎在一起玩蹺蹺板一樣，兩邊相等，很平衡。”

教師沒有馬上接口，暗自思考該如何評價，其他學生卻很受“啟發”，紛紛舉手要發言。教師一看學生學習熱情如此高漲，也不由得興奮起來，允許學生暢所欲言，結果又出現了以下“精彩紛呈”的舉例，讓教師大呼過癮，直至下課鈴聲響起——

生1：方程像農民伯伯挑的糞桶擔。

生2：方程像少林寺和尚用雙手提水桶練功。

生3：鳥類的翅膀就像方程一樣用來保持它們飛行時的平衡。

生4：對，飛機的兩翼也是這個道理。

生5：我們人類繁衍生存的男女比例是一半一半的，這也與方程相似吧？！

生6：科學課上學過植物鏈、動物鏈，我覺得，這生態平衡問題就像一個大大的方程。

……

【“問”：病歷記錄】

課后，筆者問學生：“你們覺得方程難學嗎？”

學生眾口一詞，都說不難，只要抓住“等式”和“未知數”兩個要點就行。

“那為什么要學方程呢？”

許多學生都說不出所以然。

筆者換了一個話題：“一輛公交車行駛到某一站，下車6人，上車4人，這時車上一共12人。這里有方程么？”

學生眾口一詞，都認為沒有，因為這里看不到天平的平衡。

筆者又換了一個話題：“你認為x=1是方程嗎？”

許多學生都認為是，因為它符合“等式”和“未知數”兩個要點。還有一些學生感覺這個方程有點怪。

筆者轉而問教師：“x=1是方程嗎？”

教師有點遲疑地說：“應該是吧，它是一個含有未知數的等式。只是這個方程也太簡單了。”

“明明x等于1，怎么可以說它未知呢？！”

“這個，……是啊，這是怎么回事呢？”教師一籌莫展。

筆者又換了一個話題：“你覺得，學生在課的最后，所說的對方程的認識是否準確？”

教師一臉無奈：“說實在的，我也說不準，但我感覺他們這樣說還是比較形象生動的。”

……

【“切”：病理診治】

數學家笛卡爾在《指導思維的法則》一書中提出了一種解決一切問題的“萬能方法”，其模式是：把任何種類的問題轉化為數學問題；把任何種類的數學問題轉化為代數問題；把任何種類的代數問題轉化為方程（組）的問題，然后討論方程（組）的問題，得到解之后再對“解”進行解釋。從中，我們可以感覺到“方程”知識的重要性，它是解決問題的重要方法，由此有專家認為“方程既非基本概念，也非基本理論，而是基本方法”。

然而，許多教師對方程的本質認識也比較模糊，這可以從課后筆者詢問教師“x=1是方程嗎？”中反映出來。

那么，方程的本質是什么？張奠宙教授對方程進行了重新定義：“方程是為了尋求未知數，在未知數和已知數之間建立起來的等式關系。”如此發生式定義首先告訴了我們方程的核心價值，即為了尋求未知數，接著告訴我們，方程乃是一種關系，其特征是“等式”關系，這種等式關系，把未知數和已知數聯系起來了，于是，人們借助這層關系，找到了我們需要的未知數。可見，“含有未知數的等式叫作方程”并非是方程的嚴格定義，僅是一種樸素的描寫，方程的意義不在于概念本身，而在于方程的本質特征：要“求”未知數，在未知數和已知數之間建立起來的等式關系。

至此，我們就不難回答“x=1是方程嗎？”這一問題，從形式上看，x=1是方程，這個式子里有未知數，也有等式，完全符合教材對方程的描述。但如果用“方程是為了尋求未知數，在未知數和已知數之間建立起來的等式關系”來看，x=1更應該說成是方程的解。否則，只會出現“數學悖論”——“明明x等于1，怎么可以說它未知呢？”

在教學中，如果教師始終只是抓住“等式”和“未知數”這兩個要點去認識方程，那永遠只能流于形式，這樣的教學就是史寧中教授所說的把思路搞反了，學生對方程的認識只是停留在熟練背誦方程定義的層面上，也就是說，這樣的教學過程只是教會了學生定義，而沒有教會學生意義。

因為“方程既非基本概念，也非基本理論”，所以我們的教學不應過分在方程的“是什么”上咬文嚼字、對號入座，而應該在方程的“為什么”上下功夫。陳重穆教授也指出：“含有未知數的等式叫作方程”這一定義中沒有體現方程的本質，這樣的定義要淡化，不要記，無須背，更不要考。真正的方程教學關鍵是要理解方程思想的本質，它的價值和意義，讓學生通過豐富的問題情景，去發現其中的相等關系，在表達這些相等關系的時候，有的不需要未知數，有時候需要未知數一起參與，下面這個教學片段就很好地讓學生明白了方程的“為什么”——

師：你今年幾歲啦？

生：11歲。

師：你的年齡是一個已經知道的數，在數學上稱為已知數。你知道老師的年齡嗎？

生：不知道。是未知數。

師：你們想把這個未知數變成已知數嗎？我的年齡減去20歲后，還比你們大。我的年齡減去30歲，比你們小。能確定我的年齡嗎？

生：不能，只是一個范圍。

師：如果我的年齡減去27就等于11呢？

生：38歲。

師：剛才給你們三條信息，為什么前面兩條信息你們不能確定我的年齡，而第三條信息一出來就能確定？（學生小組討論）

生：只有相等的式子，才能求出確定的結果。

師：怎樣把這三條信息用含有字母的式子表示？

生：x-20>11，x-30<11，x-27=11。

師：比較一下，你們發現了什么？

生：第三個式子是左右相等的。

師：是的，在未知數和已知數之間建立等量關系的式子，在數學上叫方程。

……

在小學教學中，方程是小學生首次學習有關代數的知識，是學生從算術思維向代數思維過渡的初期。然而，在訪談中學生普遍認為“方程不難”，這在一定程度上暴露了教師并沒有認識到方程的真正價值，也沒有對教學難點進行突破。

首先，我們要讓學生弄清楚等式關系這一個教學難點。學生在以前的學習中，經常做的計算題，例如“1+2=？”此時“1+2=3”中的“=”，在學生的眼里，常常被看成是一種具有運算性質的符號，然而，以前學生也曾做過諸如這樣的判斷題“在○里填>、=、<：1+2○3”，此時“1+2=3”中的“=”，教師卻常常未能及時指導學生認識到它其實就是一種關系符號。由此可見，“1+2=3”在學生的眼里更多地看成是一個算式——“1+2=？”而非一個等式——“1+2○3”，其實，“1+2=3”中的“=”在根本上就是一種關系符號。

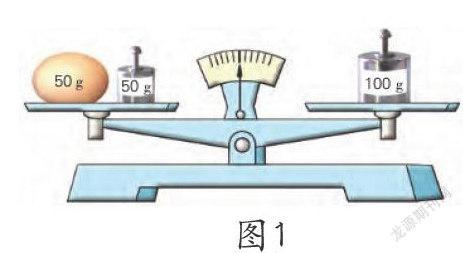
學生長久局限在算術的思維中，導致在學習方程時對“‘=’是一種關系符號”的認識感到困難，對此，教師可以復習“在○里填>、=、<：1+2○3”這樣的判斷題，勾起學生對“往事”的回憶，認識到“1+2=3”中的“=”表示相等關系。為了增加視覺效果，引起學生的注意，教師還可以在例1（如圖1）前增加這樣的鋪墊——“在天平左右兩邊各放20克砝碼”，讓學生對“20=20”在視覺上產生強烈的“不舒服”——“有這樣的算式嗎？”此時教師把“20=20”改換成“20○20”這種學生曾經做過的判斷題形式，幫助學生領悟到“20=20”表示的是一個等式，從而在對比中認識到此處的“=”是一種關系符號。

……

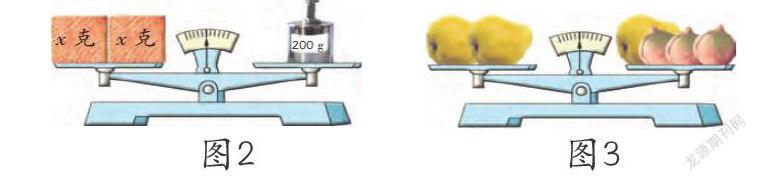
除了方程的工具價值，方程思想的感悟也是教學的重點和難點。方程思想的核心在于建模、化歸。史寧中和孔凡哲在《方程思想及其課程教學設計——數學教育熱點問題系列訪談錄之一》一文中指出：“小學四則運算僅僅提供一種算法，而一元一次方程則比較全面地展示了建模思想——用等號將相互等價的兩件事情聯立。等號的左右兩邊等價，至于其中的關系是用文字語言表示的，還是用數學符號表達的，都不太重要，重要的是等號左右兩邊的事情在數學上是等價的，這就是數學建模的本質。”在認識“方程是一種模型”的教學中，教師應該讓學生認識到“相互等價的兩件事情”不僅只是如圖2所示事物與砝碼之間的等價關系（因為學生常常將砝碼視為事物稱重的結果，此情景下的“=”，學生往往視之為運算符號），還可以是如圖3所示一種事物與另一種事物之間的等價關系（此情景下的“=”更容易讓學生清楚地認識到它是一種關系符號），從而使學生能正確地理解方程的意義。

本課教學不能停留在概念層面的理解，而應該注重讓學生經歷方程的建模過程，根據已有模式出發賦予方程合理的生活情境，在經歷方程建模的過程中深刻理解方程的意義。上述課例，從課后的測試可以看出，學生對方程的認識滿腦子只有“天平”，這對方程的建模是不利的。我們應該幫助學生跳出天平而在更大的范圍內認識方程，除了“乘車問題”，還有如下教學片段中的“倒水問題”，同樣存在著方程——

師：現在老師把看得見的天平收起來了，不知道你們的心中有天平嗎？

生：有！

師：拿出來！（學生兩手平衡表示天平）

出示題目：一個水壺，裝有2000毫升水，往兩個暖壺倒滿水，再往一個200毫升的水杯倒滿水，正好倒完。（假設一個水壺的自身重量=兩個暖壺的自身重量+一個水杯的自身重量）

師：這道題里有天平嗎？

生：沒有。

師：真的沒有嗎？

生：有！

師：在哪兒呢？拿出來。右邊2000毫升水壺，現在天平怎么樣？（學生演示）左邊倒滿一個暖壺，再倒滿一個暖壺，天平還不平衡，再加一個裝滿200毫升水的水杯，天平平衡了嗎？

師：你會列出方程嗎？

……

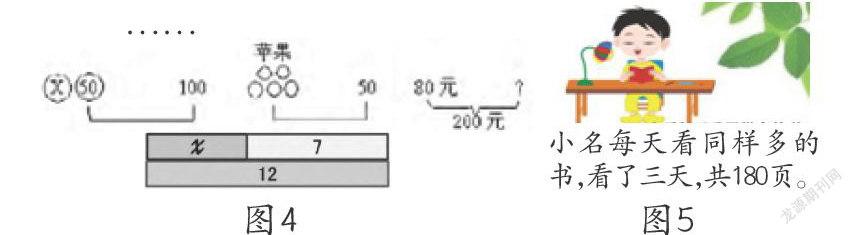
當然，上述“倒水問題”中的方程也可以只關注水的相等關系。在“乘車問題”和“倒水問題”之類的遷移中，學生會經歷一個“天平”的變異、抽象和拓展過程，例如圖4所示，“天平”變成了示意圖、線段圖等形象。如果說，圖4所示的問題還能讓學生看出“天平”，那么圖5所示的問題則更需要學生想出“天平”，這樣的抽象和變通過程是數學模型建立必須經歷的過程。

……

同時，要讓學生更好地進行方程建模，教師不妨多采用對比手法，教學可以分為兩個層次：一是同樣的問題情景可以寫出不同的方程，讓學生從不同角度尋找等量關系，體會數量間的相等關系是方程的根；二是不同的問題情景可以用同樣的方程來概括，表明了方程是刻畫現實世界的有效模型，例如設計一些諸如“你能說一說生活中還有哪些事情也用方程4x=400表示嗎？”之類的開放題。異中有同，同中有異，這也是方程的魅力所在。

上述“倒水問題”教學中，教師的高明之舉就是逐步引導學生將心中的天平代替活動的天平。學習方程，形式上的天平并不重要，重要的是心中要有“天平”——數量間的相等關系。只有心中有數量之間的相等關系，才能真正體會到這種相等關系所帶來的數學思維的變化。

經過如此深入知識本質的教學，也就能夠最大程度避免上述課例中一些學生對方程的模糊認識：一位學生的舉例——“我覺得方程就像兩個雙胞胎在一起玩蹺蹺板一樣，兩邊相等，很平衡”，其實玩蹺蹺板是以不平衡為目的，如果蹺蹺板平衡了，恰恰說明兩邊重量不相等。同樣，另一位學生的舉例——“方程像農民伯伯挑的糞桶擔”，挑糞桶擔雖然以平衡為目的，但它可以通過調節支點兩邊的距離來實現，所以平衡不一定相等。另外，這些學生的舉例都缺失了方程另一個主要元素“含有未知數”，正確地說應該是“求未知數”，在此確實可以看出學生滿腦子只有“平衡”意識。而教師在處理這些生成性問題的時候沒有及時介入作正確的指導（由此看出教師對此認識也比較模糊），導致學生的舉例走上岔路，把“方程是什么”的科學性認識開始偏向“方程像什么”的藝術化認識，最終遠離知識本質、學科本質而不亦樂乎，淡忘甚至遺忘原有的思考對象和知識目標。

教學過程是動態變化的，其隨機性造就了許許多多的生成性問題。有些生成性問題對教學有著積極作用——造就教學意外的“故事”，教師應及時開發和利用這些有益的問題，使之上升為教學的“資源”，使教學更精彩；而有些生成性問題對教學有著消極作用——造成教學意外的“事故”，教師應及時拋棄或轉化這些無益的問題，使之不演變成教學的“垃圾”，使教學正常化。

然而，教師對這些生成性問題并非都能保持清醒的認識，并能科學合理地進行處理。有的教師因本體性知識不足，對生成性問題是否正確無從判斷；有的教師誤解新課程理念，片面認定生成性問題的正面效應；有的教師審視能力偏低，判斷遲鈍，教育機智不強，顯得無所適從。所以，教師需要加強自身修煉。

（江蘇省無錫市碩放南星苑小學 214142

江蘇省無錫市錫山教師進修學校 214191）