基于CFD近似模型的船尾線型多目標綜合優化

董素貞+馮佰威+詹成勝+沈通+常海超

摘要： 為提高船體的優化效率，以國際標準船型KCS為研究對象，以船舶總阻力和槳盤面伴流不均勻度為優化目標，建立近似模型，完成KCS船尾線型的優化，得到優化船型.通過優化結果可知：對于母型船，在滿足工程約束條件下，通過船尾優化可以得到總阻力未增加、船尾流場品質有明顯改善的船體線型.

關鍵詞： 船體線型； 徑向基函數； 插值； 近似模型； 阻力性能； 伴流不均勻度； 綜合優化

中圖分類號： U663.5文獻標志碼： B

Abstract： To improve the optimization efficiency of ship hull， the international standard ship type KCS is taken as the research object. The total resistance and the wave nonuniformity at the propeller disk are taken as the optimization goals， an approximation model is built， and the KCS stern line is optimized. The optimization results indicate that， under the engineering constraint conditions， the optimization on the stern of original ship can obtain an improved ship hull line， of which the total resistance is not increased and the stern flow field quality is significantly improved.

Key words： ship hull line； radial basis function； interpolation； approximation model； resistance performance； wake nonuniformity； integrated optimization

收稿日期： 2014[KG*9〗03[KG*9〗26修回日期： 2014[KG*9〗05[KG*9〗15

基金項目： 國家自然科學基金重點項目（51039006）；國家自然科學基金（51279147， 51179143）；

高等學校博士學科點專項科研基金（20100143110010）

作者簡介： 董素貞（1991—），女，河北石家莊人，碩士研究生，研究方向為船舶多學科設計優化，（Email）suzhen_dong@126.com；

馮佰威（1974—），男（滿族），遼寧錦州人，副教授，博士，研究方向為船舶多學科設計優化，（Email）fengbaiwei@126.com0引言

近年，國際海事組織（International Maritime Organization， IMO）提出船舶能效設計指數（Energy Efficiency Design Index， EEDI），為迎接這一挑戰，必須大力開展節能船型的設計與研究.國際船舶會議 （International Towing Tank Conference， ITTC）已將基于仿真的設計（Simulation Based Design， SBD） 列為數值模擬技術研究的前沿熱點課題.國內外學者紛紛將最優化技術與先進的CFD技術結合，發展形成基于CFD的船型優化設計技術.意大利INSEAN水池的PERI等[12]、德國柏林理工大學的HARRIES等[3]、日本京都大學的TAHARA等[4]和美國喬治梅森大學的YANG等[5]，均將數值模擬技術和優化算法結合，建立基于CFD的船型優化設計平臺，完成船體線型的仿真優化設計.馮佰威[6]、梁軍[7]、張寶吉[8]和李勝忠[9]等對船型優化進行深入研究，取得不錯的成果.然而，上述研究大多以船體水動力性能為優化目標，很少考慮優化船型的尾流場品質.艉流場不僅影響船舶的推進效率，而且還對螺旋槳空泡剝蝕、艉部激振、噪聲以及船體振動等產生影響.

本文以國際標準船型KCS為研究對象，以船舶總阻力和槳盤面伴流不均勻度為優化目標，優化KCS艉部形狀，期望得到阻力和艉流場品質有明顯改善的船體線型.

1基于CFD近似模型的船型優化框架為保證船型優化結果的可靠性，需要準確的水動力性能數值預報工具.傳統做法是將CFD軟件直接應用于優化進程中，雖能保證優化的準確度，但計算成本高，優化效率低；若在優化前采用CFD對多條樣本船舶進行水動力計算，并根據計算結果建立高精度的近似模型，然后在優化過程中利用近似模型代替耗時的CFD計算，能有效解決這一問題.基于CFD近似模型的船型優化流程見圖1.

1）船型參數化修改模塊依據設計變量進行船體曲面的變形，同時計算各類約束條件.

2）用近似模型代替CFD求解器，并預報相關性能指標（目標函數）.

3）優化器根據目標函數和約束條件信息判斷是否停止，若沒有達到停止條件，則通過優化算法改變設計變量的值.

4）新的設計變量傳遞給船型參數化修改模塊，再重復1～3.

由圖1可知，船型參數化修改和近似模型構建是實現船型優化的關鍵.船型參數化修改決定設計變量的空間形式，而近似模型的精確度決定優化結果的可靠性.

2基于徑向基插值的船體曲面修改

利用徑向基函數插值（原理見文獻[10]）實現船體曲面修改，其優勢在于：在進行船體變形時可以固定水線、甲板邊線等控制點，以保留母型船的特定線型，方便工程師在總布置等方面的設計.對韓國船舶與海洋工程研究所的集裝箱船KCS（見圖2）進行艉部曲面修改.該船的主要參數見表1.

根據經驗，在船體曲面的舯、艉部選擇9個可變控制點（即變量），分別編號為1～9，見圖3.控制點的變動方向均為y方向（船寬方向）.以使船型曲面不發生太大變化為原則，確定變量的變化范圍.變量的初始值為標準模型數據，見表2.為保證加工制造的可行性，將處于船體中縱剖線上、甲板邊線上以及靠近舯橫剖面上的網格控制點作為優化過程中的不變點，在圖3中用粗實線表示.

3KCS水動力計算和近似模型建立

3.1KCS船體阻力和伴流計算精度驗證

利用水動力軟件SHIPFLOW計算得到弗勞德數Fr為0.25，0.26和0.27時KCS船模的阻力和伴流場信息.興波阻力計算采用勢流理論，黏性阻力計算采用kω SST湍流模型.為降低網格對計算的影響，采用由疏到密3套不同網格密度，分別記為coarse， medium和fine進行CFD計算.3套網格中，興波計算采用面元網格， 黏性計算采用全結構化六面體網格.coarse密度時網格數量為44.6萬個，medium密度時網格數量為74.4萬個，fine密度時網格數量為121.8萬個.

船體總阻力因數曲線的計算結果與試驗結果對比見圖4.當Fr=0.26時船尾螺旋槳盤面上槳軸高度處流場的軸向速度（u/U）在船體側向的分布情況見圖5.試驗數據采用Gothenburg 2000，Tokyo 2005和Gothenburg 2010等會議資料中公布的相關數據.

由圖4可知：網格fine比網格coarse和medium的阻力結果更接近試驗結果，網格medium與網格coarse計算結果相比精度相當；3套網格下阻力結果的趨勢與試驗結果趨勢均相同.由圖5可知：不同網格密度下的艉流場模擬結果的差異很小，且均較接近試驗結果.綜合來看，在不同網格質量下計算結果的趨勢相同，網格加密對阻力和流場的計算精度有利.因此，首先采用粗網格對船型樣本進行水動力計算，建立以總阻力和伴流不均勻度為目標的近似模型；然后為驗證優化結果，采用加密的網格對優化船型進行水動力計算.

3.2近似模型的建立

船舶CFD計算復雜且耗時多，一直是困擾船體線型優化研究的難點之一，將近似理論引入到船體線型優化中可以有效解決這一難題.

1）建立典型樣本庫，即對典型船型進行水動力性能數值模擬，并在此基礎上建立樣本庫.

2）模型選擇和模型的擬合.針對樣本庫中數據的特點，選擇合適的近似模型.以船型的特征參數為輸入參數，以水動力性能指標為響應的輸出參數，采用最小二乘回歸等方法對近似模型進行數據回歸擬合，求得相關待定系數，建立近似模型.

3）模型檢驗.近似模型建立之后，根據統計學中的方差分析原理，利用新的數據樣本對模型進行檢驗.如果模型擬合與預測精度都滿足要求則建模結束，否則重新構造近似模型，直到其擬合與預測精度滿足要求.

4）近似模型的使用.在優化進程中，將近似模型代替耗時的數值計算驅動優化，根據船型特征參數快速預報和優化水動力性能指標.

3.2.1樣本點的選取

采用均勻試驗設計方法[11]，選取200個船型樣本點進行CFD數值計算.計算中，面元網格采用medium網格，體網格采用coarse網格，計算得到船型樣本點的總阻力和伴流場信息.選取的部分船型樣本點見表3，部分變量的投影圖見圖6，其中y1y2代表變量y1和y2所在的二維平面，y8y9代表變量y8和y9所在的二維平面.由圖6可知，變量在二維平面內均勻分布.

3.2.2神經網絡建模

通過水動力計算得到船舶阻力和艉流場信息，計算槳盤面伴流不均勻度Wf.采用神經網絡對生成的樣本集進行系統建模，訓練算法為LM算法，激活函數采用tanh函數，經訓練得到總阻力和Wf的近似模型.為驗證近似模型的精度，另外隨機選擇100個方案作為測試點，利用CFD軟件進行數值計算，并與近似模型預報的結果進行比較.訓練點與測試點的Wf誤差比較見圖7，訓練點與測試點的總阻力因數Ct誤差比較見圖8.

a）訓練點

b）測試點

Tab.4Values of ERMS and EMAP指標類型ERMSEMAP/%Wf訓練點0.002 971.42測試點0.004 071.71Ct訓練點0.000 016 520.34測試點0.000 020 140.43由表4可知，訓練點2個指標的ERMS和EMAP值均很理想，說明訓練的神經網絡模型精確度較高，可將該模型應用于船型優化中.

4KCS船總阻力和艉流場的優化

4.1基于近似模型的船型優化流程

基于近似模型的船型優化流程見圖9，具體過程如下：

1）對選取的設計變量賦初值.

2）基于RBF修改方法生成船型曲面.

3）若滿足約束條件則到步驟4，否則回步驟1.

4）利用神經網絡近似模型預報目標值.

5）采用多目標遺傳算法優化設計變量，判斷是否收斂.

6）若不收斂，則重復步驟2～5，直到收斂或達到迭代次數.

4.2優化數學模型的建立

4.2.1優化目標

優化目標有2個，即Ct最小、伴流場質量最好.伴流場質量的衡準很多，常用的衡量艉流場不均勻度的方法有BSRA五項衡準，其對艉流場各因素進行綜合考慮，但對大量結果進行比較判斷時較繁瑣；另有荷蘭MARIN水池提出的伴流目標函數 （Wake Objective Function， WOF）方法[12]，WOF數值越小，說明伴流越均勻.PERI等[13]定義的槳盤面伴流不均勻度Wf=Ni1MMj（Vxij-V-xi）2（3）式中：M為槳盤面沿周向的等分數目；N為槳盤面沿徑向等分的數目；Vxi為槳盤面半徑為Ri/N，角度為2πj/M處對應的無因次軸向伴流速度；V-xi為槳盤面半徑Ri/N處各角度的無因次軸向速度平均值.

選取具有代表性的0.7R（R為槳盤面半徑）處采集的M個不同角度處伴流速度的標準差作為Wf的評判標準，即Wf=1MMj（V-V-）2（4）式中：V為槳盤面角度為2πj/M處對應的無因次速度；V-為槳盤面各角度處無因次速度的平均值.

因此，優化目標為min f1=Wf

min f2=Ct，Fr=0.26（5）4.2.2優化變量取值范圍

優化變量的取值范圍見表2.

4.2.3約束條件

船寬B、吃水T均保持不變，艏部線型不變，僅變動艉部線型.為使船舶的載質量以及浮態等不致發生太大改變，限制排水量和浮心縱向位置的變動在1%范圍內.約束條件為Δ-ΔoptΔ≤0.01（6）

L-LoptL≤0.01（7）式中：Δ為母型的排水量，t；L為浮心距舯縱向距離，m；Δopt和Lopt分別為優化船的排水量和浮心距舯縱向距離，單位分別為t和m.

4.3優化結果分析

4.3.1優化結果

優化算法采用遺傳算法，其種群規模設置為50，遺傳代數設置為80，優化后產生Pareto前沿（非劣解解集）見圖10.

優化算例顯示：在Pareto前沿上，Ct越小，伴流均勻性越差.Wf越小，Ct往往越大.設計人員可以依據性能要求的不同，在Pareto前沿上選擇合適的設計方案.

4.3.2網格加密后的數值計算結果分析

為進一步驗證優化效果，從Pareto非劣解集中選取Wf目標值小于母型船且Ct未增大或增大較少的6個方案，分別記為Opt 1～6，加密網格后再進行CFD計算，黏性迭代次數為2 000步，網格數約為120萬個.

優化方案及母型船的總阻力值與Wf的對比見表5.由此可知：優化方案Opt 1～6的總阻力依次減小，而Wf的對比依次上升；0.7R處Wf的對比有明顯下降，總不均勻度也有所下降.雖然優化船的Ct優化效果明顯，但由于船體濕表面積的增大，導致總阻力的優化效果不明顯.

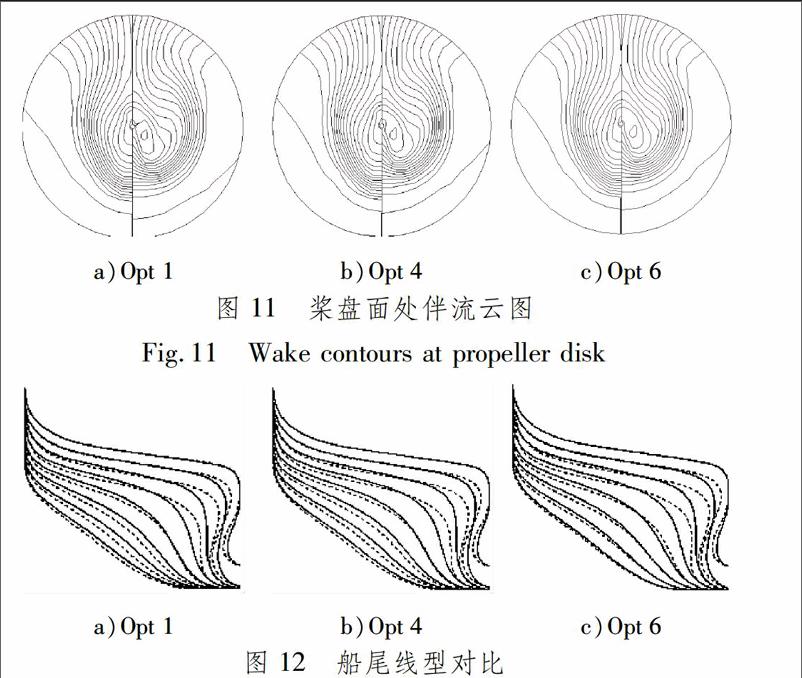
從以上6個優化方案中，選取3個優化方案Opt 1，Opt 4和Opt 6進行分析.Opt 1，Opt 4和Opt 6與母型船槳盤面處伴流云圖見圖11，其中每個子圖的左半部為母型船、右半部為優化船.由此可知，在大半徑處優化船的伴流等值線更接近同心圓.艉部線型比較見圖12，其中實線為母型船、虛線為優化船.

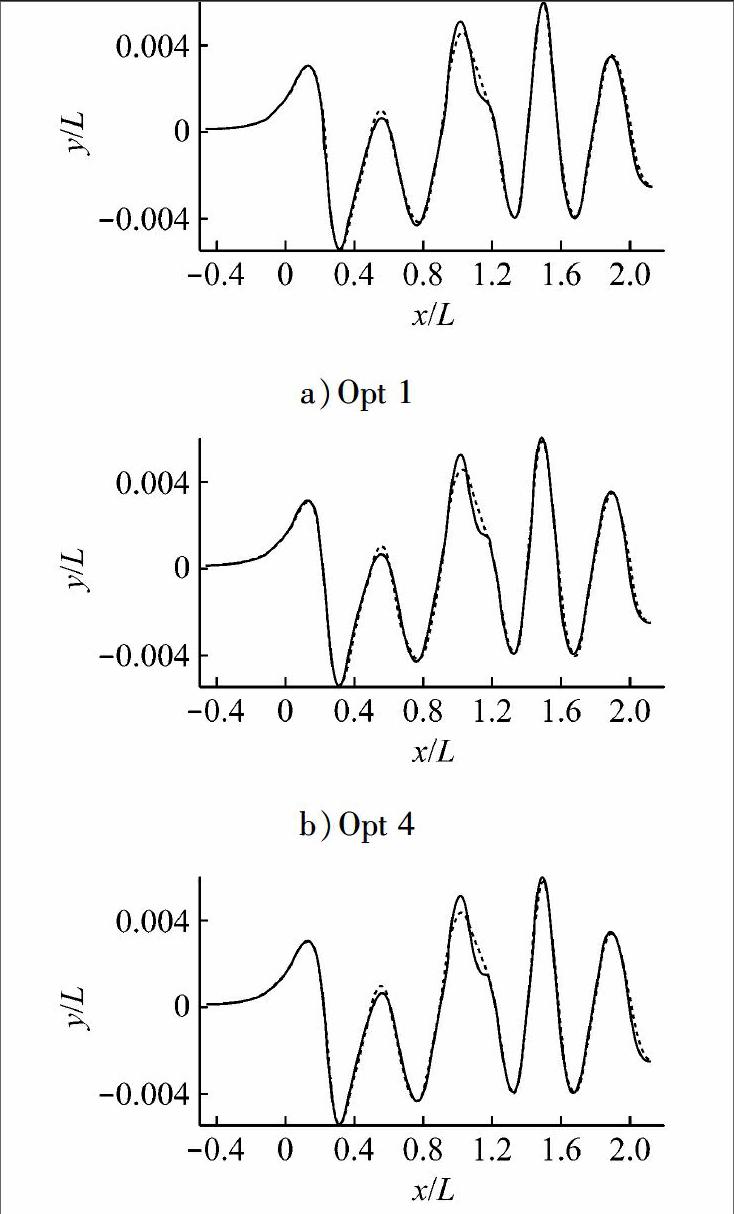
由圖12可知，優化船的艉軸處線型更“扭曲”，艉軸附近的形狀適當下沉，有利于艉部Wf的改善.由于艉軸上方線型內凹，使更多的流體流動至此，并向螺旋槳盤面處流動，改善不均勻狀況.優化船和母型船在船側y/L=0.1處水動力計算所得的波切圖對比見圖13，其中實線為母型船、虛線為優化船.

由于沒有對舯前部分線型進行修改，因此舯前波高變化非常小，而舯后部分尤其是船尾處波高有所下降，所損耗的能量變少，是阻力下降的原因之一.

Opt 1，Opt 4和Opt 6與母型船的槳盤面0.7R處伴流速度及槳盤面不同半徑處伴流速度均值見圖14.由此可知，當約θ<30°時優化方案0.7R處伴流速度大于母型，當約θ>30°時則相反，表明伴流速度沿周向的波動較母型船小；伴流均值在r/R<0.3處大于母型船，在r/R>0.3處則相反，表明伴流速度沿徑向的波動較母型船小.

a）0.7Rb）不同半徑

5結論

以KCS船為初始船型，對其艉部線型進行優化，結論如下.

1）RBF曲面插值方法不僅能保證曲面的光順性，而且使局部線型的變形更為靈活，極大地拓寬船型變化的設計空間.

2）利用均勻設計方法進行樣本點的選取，實例驗證表明：應用該方法選取的樣本點能夠均勻散布于整個變量空間，為構建高精度的近似模型提供必要的前提條件.

3）為提高優化效率，根據低精度水動力計算結果構建神經網絡近似模型，并將其應用于船舶優化中，結果表明，神經網絡模型對于變量維數較高、性能空間復雜的非線性問題具有良好的適用性.

4）在Fr=0.26時，對KCS船進行艉流場和總阻力的多目標優化研究，得到槳盤面處艉流場伴流不均勻度明顯改善且總阻力基本未增加的優化船型.參考文獻：

[1]PERI D， CAMPANA E F. Multidisciplinary design optimization of a naval combatant[J]. J Ship Res， 2003， 47（1）： 112.

[2]PERI D， CAMPANA E F， DATTOLA R. Multidisciplinary design optimization of a naval frigate[C]//Proc 10th AIAA/ISSMO Multidisciplinary Anal & Optimization Conf. Albany， 2004： 4613.

[3]HARRIES S， VALDENAZZI F， ABT C， et al. Investigation on optimization strategies for the hydrodynamic design of fast ferries[C]//Proc 6th Int Conf Fast Sea Transportation. Southhampton， 2001： 5356.

[4]TAHARA Y， STERN F， HIMENO Y. Computational fluid dynamicsbased optimization of a surface combatant[J]. J Ship Res， 2004， 48（4）： 273287.

[5]YANG C， KIM H. Hull form design exploration based on response surface method[C]// Proc 21st （2011） Int Offshore & Polar Eng Conf. Maui， 2011： 816820.

[6]馮佰威. 基于多學科設計優化方法的船舶水動力性能綜合優化研究[D]. 武漢： 武漢理工大學， 2011.

[7]梁軍. 基于水動力性能的線型優化[D]. 上海： 上海交通大學， 2008.

[8]張寶吉. 船體線型優化設計方法及最小阻力船型研究[D]. 大連： 大連理工大學， 2009.

[9]李勝忠. 基于SBD技術的船舶水動力構型優化設計研究[D]. 北京： 中國艦船研究院， 2012.

[10]沈通， 馮佰威， 劉祖源， 等. 基于徑向基函數插值的船體曲面修改方法研究[J]. 中國造船， 2013， 54（4）： 4554.

SHEN Tong， FENG Baiwei， LIU Zuyuan， et al. Research of hull form modification method based on radial basis function interpolation[J]. Shipbuilding China， 2013， 54（4）： 4554.

[11]常海超， 馮佰威， 劉祖源， 等. 近似技術在船型阻力性能優化中的應用研究[J]. 中國造船， 2012， 53（1）： 8898.

CHANG Haichao， FENG Baiwei， LIU Zuyuan， et al. Research on application of approximate model in hull form optimization[J]. Shipbuilding China. 2012， 53（1）： 8898.

[12]van DER P A， HOEKSTRA M. Multiobjective optimization of a tanker after body using PARNASSOS[EB/OL]. （20091031）[20140610]. http：//www.marin.nl/web/Publications/Publicationitems/ MultiobjectiveOptimizationofaTankerAfterbodyusingPARNASSOS.htm.

[13]PERI D， CAMPANA E F. Highfidelity models and multiobjective global optimization algorithms in simulationbased design[J]. J Ship Res， 2005， 49（3）： 159175.