非線性矩陣方程X+A*X-qA=Q的Hermite正定解

霍金丹，梁麗，于嬌

(東北林業(yè)大學(xué))

0 引言

在這里要給出方程

正定解存在的充分和必要條件，其中A是n階非奇異復(fù)矩陣，Q是n階Hermite正定陣，且q≥1，X為未知矩陣，這樣的非線性矩陣方程在梯形網(wǎng)絡(luò)，隨機(jī)過(guò)濾，動(dòng)態(tài)規(guī)劃和統(tǒng)計(jì)中應(yīng)用廣泛［1-2］，同時(shí)通過(guò)眾多的學(xué)者的研究學(xué)習(xí)也取得了一定的成績(jī).

該文中遇到的難題都可以根據(jù)Banach的不動(dòng)點(diǎn)定理和Brouwer不動(dòng)點(diǎn)定理來(lái)解決，接著根據(jù)方程(1)正定解存在的充分和必要條件求出方程的解，最后又給出了求解方程(1)正定解的另一種方法，即迭代法，與此同時(shí)又給出了推導(dǎo)迭代法收斂的一個(gè)充分條件.

1 引用定理

引理 1.1［5］令B∈Cn×n，U∈Cn×k，V∈Ck×n且B，B-UV是非奇異的，則

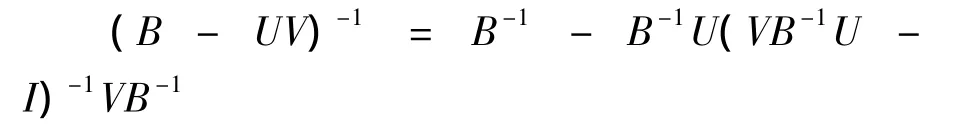
引理1.2［6］令A(yù)和B是Hilbert空間H上的正算子，且

M1Ⅰ≥A≥m1Ⅰ≥0，M2Ⅰ≥B≥m2Ⅰ＞0和B≥A＞0，

則

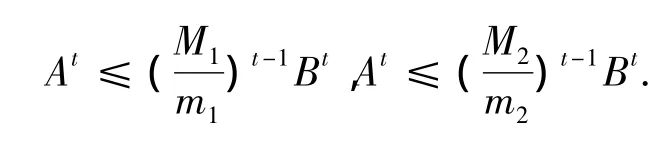
引理1.3［7］令f為在(0，∞)上的單調(diào)函數(shù)的算子，且令A(yù)、B為兩個(gè)與a有關(guān)系下界的正定算子，即A＞aⅠ和B＞aⅠ，其中a為正數(shù)，如果存在f＇(a)，則對(duì)于每一個(gè)酉不變范數(shù)‖·‖，有

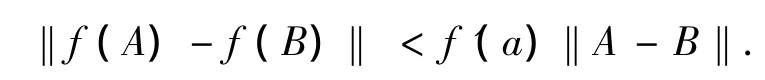
2 主要定理及證明

定理2.1 如果方程(1)有一個(gè)正定解X，則

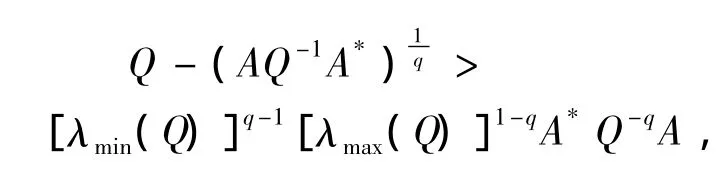
且X∈ (S，T)，這里

證明 由于X是方程(1)的一個(gè)正定解.則有X＜Q，A*X-qA＜Q，根據(jù)不等式性質(zhì)，后一個(gè)不等式可變?yōu)椋瑫r(shí)也有Q-1＜X-1，則根據(jù)引理1.2，上面兩式變?yōu)閄q＜①和②，又由方程(1)可變形為

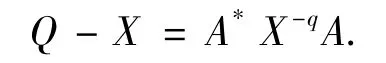
則有

即

則

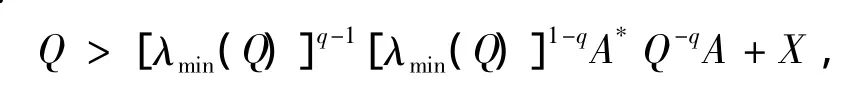
則有

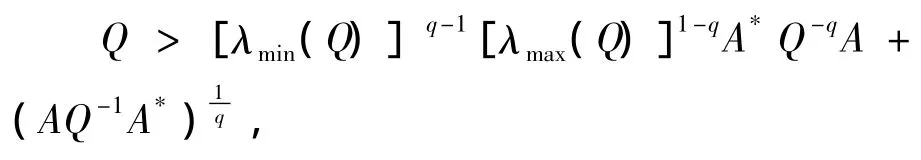
即

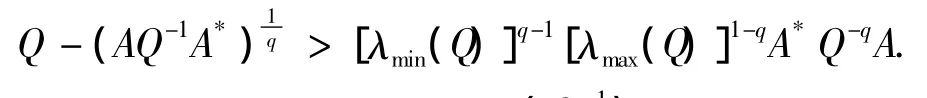
則有

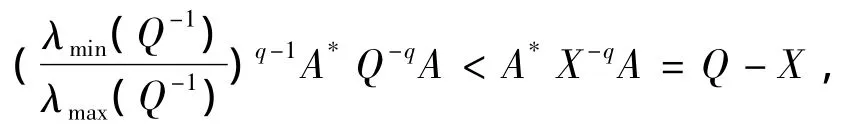
即

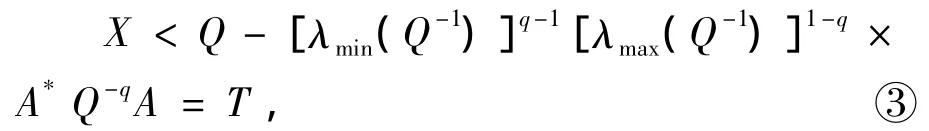
另一方面，由于方程(1)為X+A*X-qA=Q，它可變形為

則由引理1.1可得

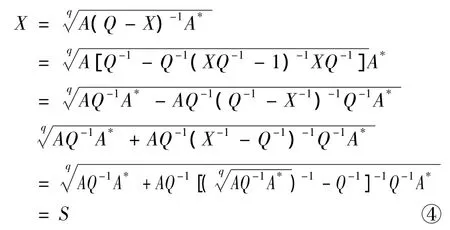
由上述的③和④，則有X∈(S，T).

注2.1 根據(jù)定理2.1可知

定理2.2 如果當(dāng)X∈時(shí)，

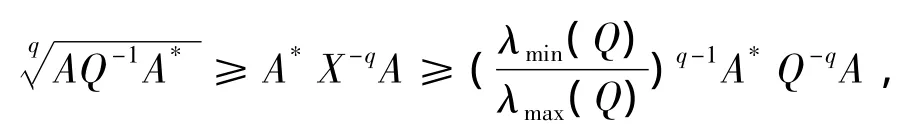
則方程(1)有正定解，且如果

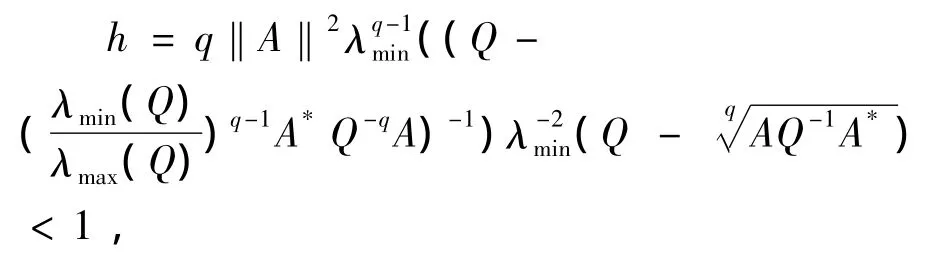
則方程(1)有唯一的正定解.

證明 考慮映射G(X)=Q-A*X-qA，且令

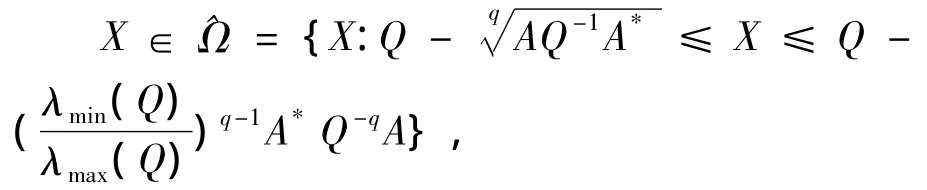
顯然，是一個(gè)凸閉集且有界，并且G(X)是上的連續(xù)函數(shù).當(dāng)X∈時(shí)，有

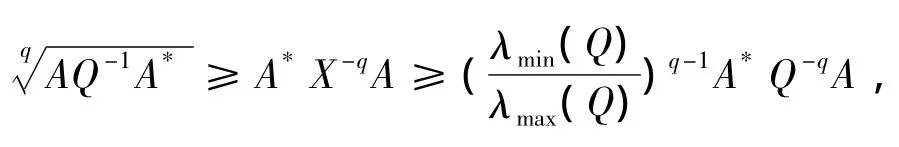
則又有

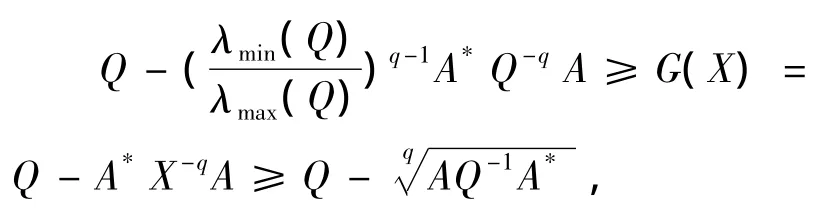
即

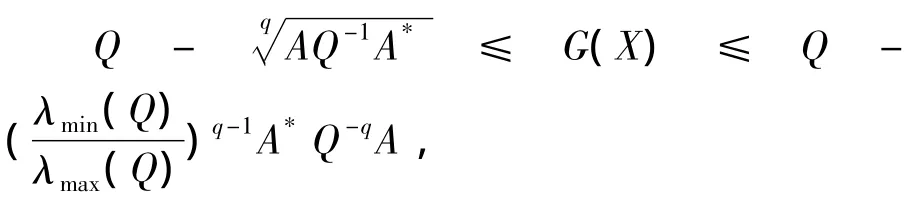
因此有G(X)?.

根據(jù)Brouwer不動(dòng)點(diǎn)定理，G(X)在區(qū)間上存在不動(dòng)點(diǎn)，且它就是方程(1)的一個(gè)解.

對(duì)于?X1，X2∈，有

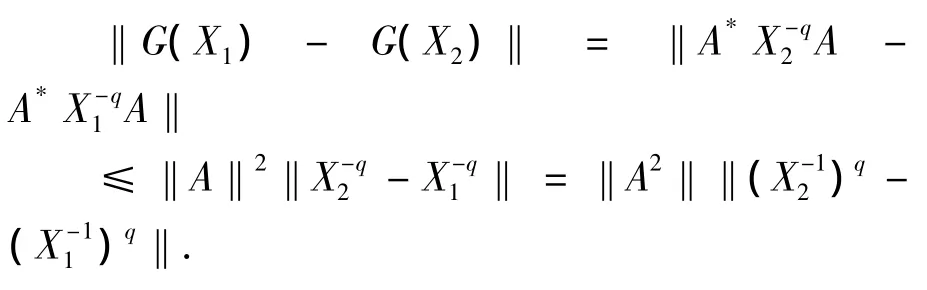
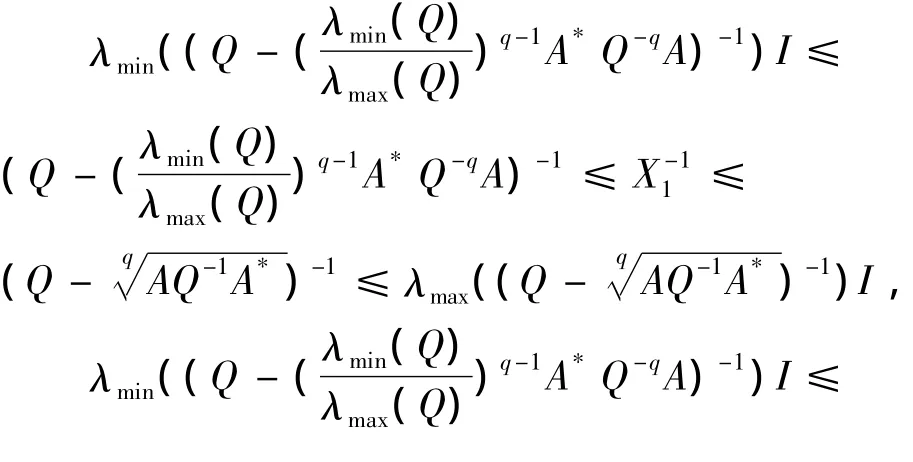
則由引理 1.3，有

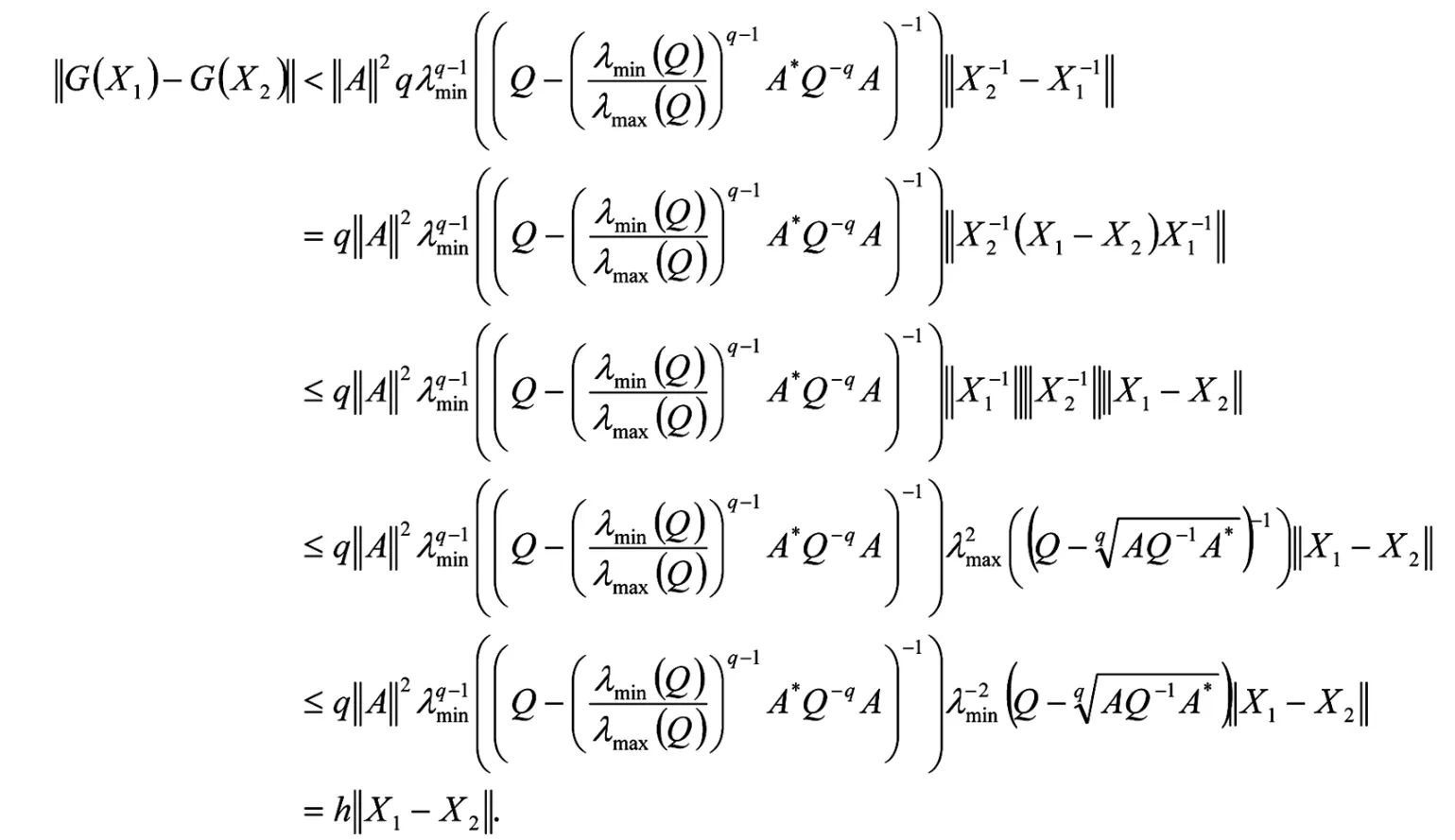
由于h＜1，所以G(X)為上的壓縮算子，又由Banach的不動(dòng)點(diǎn)定理可知G(X)在上有唯一的不動(dòng)點(diǎn)，并且這個(gè)不動(dòng)點(diǎn)是方程(1)的唯一正定解.

3 用迭代法求矩陣方程的正定解

在這一部分提出了求解方程(1)的迭代法和推導(dǎo)迭代法收斂的一個(gè)充要條件，通過(guò)考慮下面的迭代方法:

這里γ＞0.

定理3.1［8］如果方程(1)有正定解，則當(dāng)時(shí)，由(1)確定的序列{xk}是單調(diào)遞增并收斂于矩陣方程(1)的最小正定解Xs.

［1］ Anderson W N，Morley T D，Trapp G E.Positive solutions to.Linear Algebra Appl，1990，134:53-62.

［2］ Engwerda J C.On the existence of a positive definite solution of the matrix equatio.Linear Algebra Appl，1993，194:91-108.

［3］ Chen X，Li W.On the matrix equation:solution and perturbation analysis.Math Num Sin，2005，27:303-310.

［4］ Guo C，Lancaster P.Iterative solution of two matrix equations，Math Comput1999，68:1589-1603.

［5］ Gene H.Golub，Charles F.Van Loan，Matrix Computations，3rd ed.，The Johns Hopkins University Press，Baltimore and London，1996.

［6］ Furuta T.Operator inequalities associated with Holder-Mc-Carthy and Kantorovich inequalities.J Inequal，1998:137-148.

［7］ Bhatia R.Matrix analysis Springer，Berlin，1997.

［8］ Duan Xuefeng，Liao Anping.On the nonlinear matrix equation［J］.Mathematical and Computer Modeling，2009，49:936-945.