一類帶有交錯擴散項的捕食-食餌模型的分歧分析*

廖思源

(哈爾濱師范大學)

0 引言

捕食-食餌系統一直是生態學和生物數學研究的重要內容，其理論研究主要包括系統平衡點的穩定性、極限環的存在性、正解的存在性和穩定性以及分歧等問題，其中正解若存在，則表明在一定參數區域內捕食者和食餌能夠共存.

在［1］中Leslie和Gower提出如下經典的捕食-食餌模型

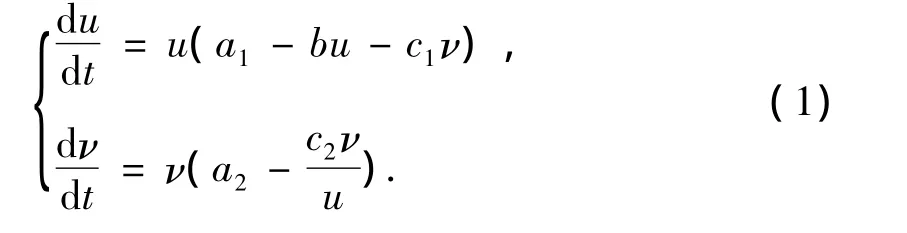
(1)可以看做是生態學研究中捕食-食餌系統的原型，但是其相互作用項是無界的，這在現實中是不合理的.通過利用在文獻［2］中提到的關于食餌和捕食者相互作用項的HollingⅡ型響應函數，可以得到如下帶有飽和響應函數的Leslie-Gower捕食 -食餌模型

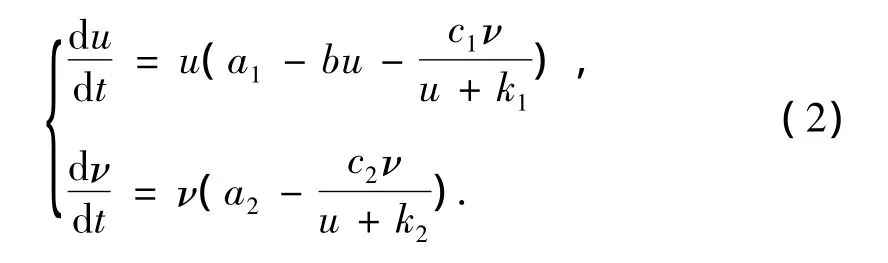
模型(2)是建立在這樣的生物學事實上:如果捕食者從它最喜歡的食物(食餌u)轉移到其它可選食物上的能力越強，那么當食餌種群數量低的時候其生存能力就越強.

由于種群會從高密度區域向低密度區域遷徙，在文獻［3-4］中考慮了如下帶有擴散項的Leslie-Gower模型

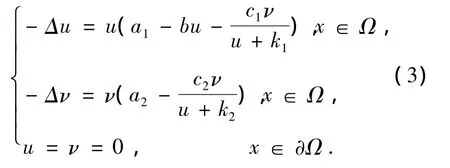
文獻［3］中討論了模型(3)在某些參數條件下正解的存在性.文獻［4］中考慮了其正解的多解性以及在特定條件下正解的唯一性，并給出了一些數值模擬的結果.

在遷徙中，食餌有向捕食者密度低的區域逃離的趨勢，這可以用交錯擴散項來刻畫.在文獻［5］中討論了Dirichlet邊值條件下帶有交錯擴散項和HollingⅡ型響應函數的如下Leslie-Gower捕食 -食餌模型.

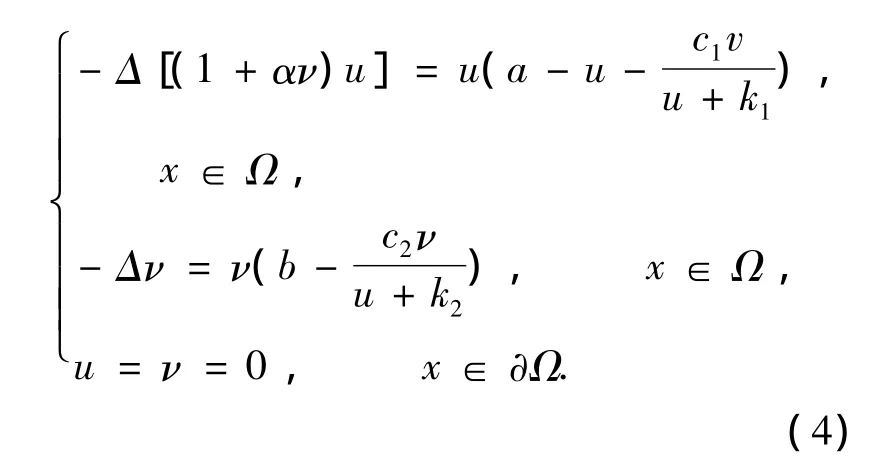
文獻［5］中討論了系統(4)正解的存在性和多解性，以a為參數考慮了系統從其中一支半平凡解支(0，k2θb/c2)上發生的分歧.該文以b為參數給出了系統(4)從另一支半平凡解(θa，0)上發生的分歧.

對于任意的q∈C()，特征值問題

的主特征值我們記為λ1(q)，對應的特征向量記為φ1(x)，并且記λ1(0)=λ1，φ1(0)=φ1.

引理［6］考慮如下logistic方程

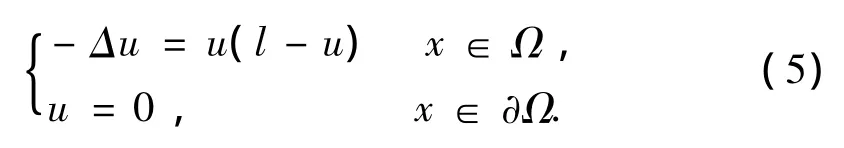
其中l是正常數，Ω?RN是邊界光滑的有界開集.

(i)如果l≤λ1，那么系統(5)沒有非平凡解.

(ii)如果l＞λ1，那么系統(5)存在唯一的正解θl(x)，并且0＜θl(x)＜l，x∈ Ω.

1 主要結果

記θa和θb分別為l=a和l=b時系統(5)的唯一正解，那么系統(4)存在平凡解(0，0)，當a＞λ1時，存在半平凡解(θa，0);當b＞λ1時，存在半平凡解(0，k2θb/c2).這里我們討論從半平凡解支(θa，0)上發生的分歧.

定理1 設a＞λ1，那么λ1是系統(4)從半平凡解曲線Γ0={(b，θa，0):b＞0}上出發的分歧值.進一步地，在(，θa，0)點附近，系統(4)的所有正解都在光滑曲線Γ1={(b(s)，u(s)，v(s)):s∈(0，δ)}上，使得對于某個δ＞0滿足

其中φ1=(-Δ+2θa-a)-1［(-αθab-)是從(0，δ)到R×X×X上的光滑函數，b1(0)=0，u1(0，x)= ν1(0，x)=0，并且

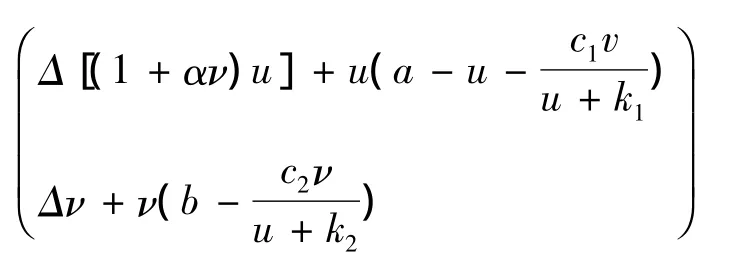
通過直接計算可得

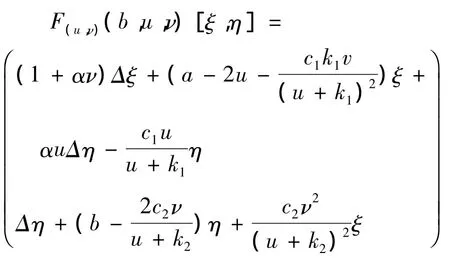
當(u，ν)=(θa，0)時，分歧發生的一個必要條件是F(u，ν)(b，θa，0)［ξ，η］ = μ［ξ，η］的主特征值等于0，即

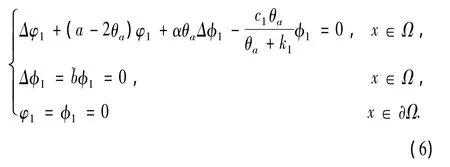
這只有當b==λ1時滿足，因此，分歧點為(b，u，ν)=(，θa，0)又由于 λ1(2θa-a)＞λ1(θa-a)=0，所以(-Δ+2θa-a)-1可逆，定義那么 核 空 間=span{(φ1，φ1)}且 dimN(=1.

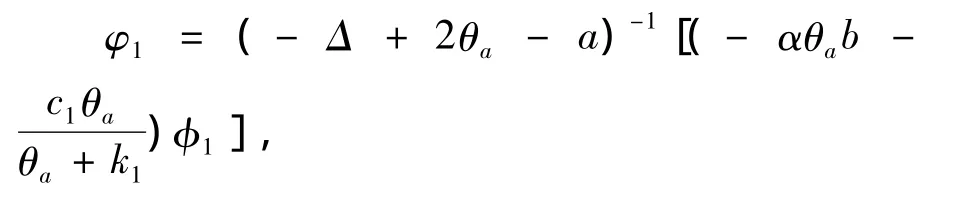
假設對任意的(f，g)∈Y×Y，存在(ξ1，η1)∈X×X，使得

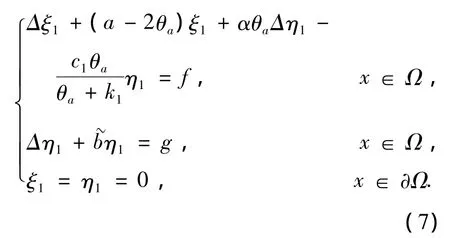
用(7)的第二式乘以φ1減去(6)的第二式乘以η1再在Ω上積分得∫Ωgφ1dx=0，因此θa，0)的像空間為

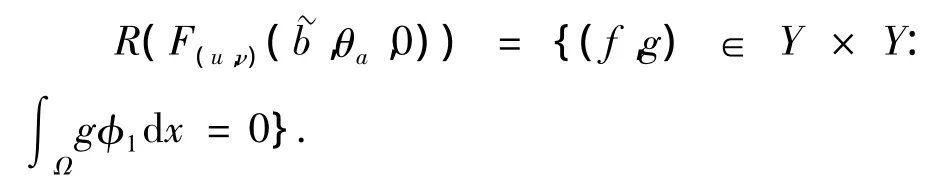
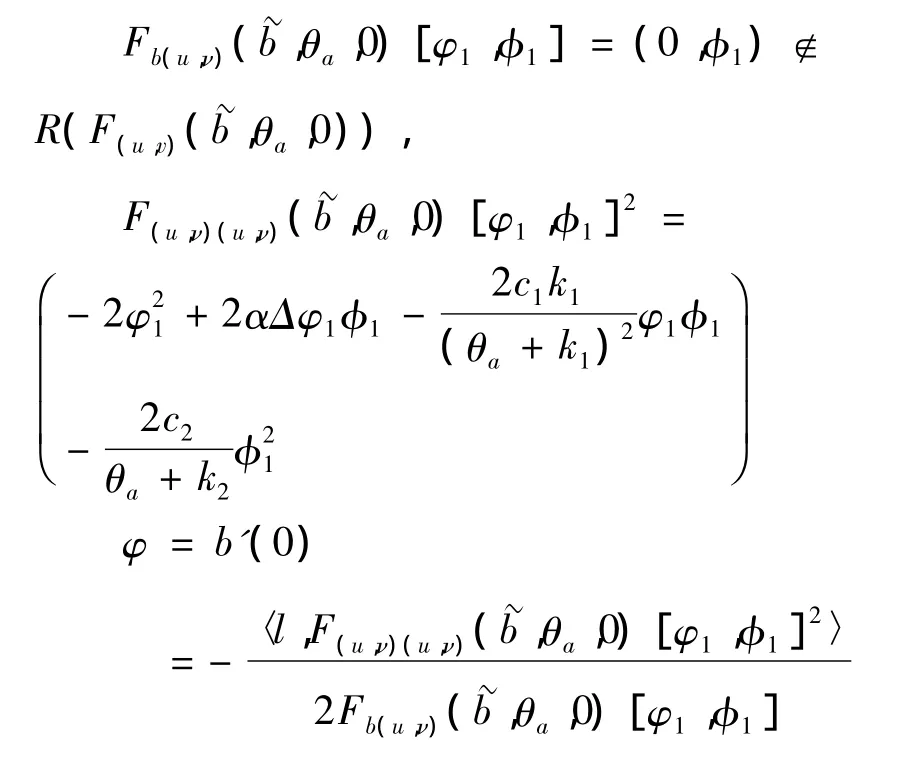
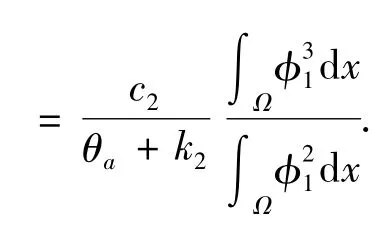
其中l是Y×Y上的線性泛函，定義

［1］ Leslie P H，Gower J C.The properties of a stochastic model for the predator-prey type of interaction between two species［J］.Biometrika，1960，47:219 ～234.

［2］ Holling C S，Some characteristics of simple types of predation and parasitism［C］.Entomol，1959，91:385-398.

［3］ Zhou J.Positive Solutions of a Diffusive Predator– prey Model with Modified Leslie-Gower and Holling-type II Schemes［J］.Math Anal Appl，2012，389:1380-1393.

［4］ Zhou J，Shi J P.The Existence，Bifurcation and Stability of Positive Stationary Solutions of a Diffusive Leslie-Gower Predator-prey Model with Holling-type II Functional Responses［J］.Math Anal Appl，2013，405:618-630.

［5］ Zhou J，Kim C G，Shi J P.Positive Steady State Solutions of a Diffusive Leslie-Gower Predator-prey Model with Holling-type Ⅱ Functional Response and Cross-diffusion［J］.Discrete and Continuous Dynamical Systems，2014，34:3875-3899.

［6］ Dancer E N.On positive solutions of some pairs of differential equations，Trans.［A］.Math Soc，1984，284:729-743.