一種模塊化機械臂的設計與運動學分析

閆繼宏，郭 鑫，劉玉斌，趙 杰

(機器人技術與系統國家重點實驗室(哈爾濱工業大學)，150001哈爾濱)

傳統的機器人大都是應用戶的要求，“一個用戶，一次重新設計”，產品規格多，零件的通用性差，而且質量和可靠性都不穩定.針對這種情況，美國卡納基梅隆大學［1-2］、日本東芝公司［3］、德國雄克(SCHUNK)公司［4］、哈爾濱工業大學機器人所［5-7］等開展了模塊化機械臂的研究，并取得了一定的成果，但是目前仍存在著機械臂模塊體積大、質量重、力矩小等問題.同時，由于模塊化機器人可以利用不同模塊組裝成各種不同的構型，給機械臂的運動學求解帶來了很大難度.雖然國內外都開展了相關的研究［8-13］，但仍未找到一種通用性強、可靠性高的運動學模塊化算法.

本文主要對機械臂結構模塊化、控制系統模塊化進行了分析和設計，并對能夠根據機械臂構型自動進行運動學求解的運動學算法進行了研究，最后以六自由度模塊化機械臂為例，對運動學算法進行了求解和仿真驗證.

1 機械臂結構模塊化設計

1.1 模塊化關節設計

機械臂模塊化關節是集機械結構、驅動、控制和通信于一體的機電一體化產品，在設計時不僅要考慮模塊自身的結構和尺寸，而且要具有良好的通用性和互換性，以便快速組裝成不同的構型.

圖1為設計的關節模塊結構，其電氣結構如圖2所示.整個關節的模塊化結構主要由驅動、傳動、反饋控制和走線等部分組成，通過機械結構與電氣的模塊化設計，實現關節模塊在機械與電氣兩個方面的模塊化.

圖1 關節模塊結構

圖2 關節模塊電氣結構

從圖1中可見，模塊采用直流伺服電機作為驅動裝置，采用諧波和齒輪二級減速的傳動方式，利用絕對式光電編碼器和扭力盤作為反饋控制裝置，通過制動器提供斷電保護.整個關節模塊結構緊湊，質量輕，輸出力矩大.直流電機、編碼器、制動器分別通過齒輪套與同一個中心齒輪連接，采用軸線平行的布置方式，使關節模塊結構更加緊湊，大大減小了關節尺寸;各個支撐、連接零件采用鋁合金進行加工制造，在保證剛度和強度的同時減輕了整個關節的質量;二級減速實現了較大的減速比，使關節輸出力矩增大.模塊走線通過電機偏置和零件的中空軸來實現，從而解決了電纜纏繞和磨損的問題.

每個關節模塊中具有相同的動力和信號連接轉接板，動力由24 V直流電源提供，信號傳遞采用CAN總線串聯的方式.驅動器根據絕對編碼器和扭力盤反饋的信息對電機和制動器等進行控制.

1.2 連桿模塊設計及機械臂構型選擇

各關節之間的運動學參數由兩者之間的連桿來確定，連桿模塊是確定構型的另一重要模塊.設計了軸線垂直形式和軸線平行形式的連桿模塊用于關節模塊之間的連接.另外，為了構型方便，模塊之間采用了螺紋快速連接結構.其結構如圖3所示.

圖3 連桿模塊結構

各個關節模塊和連桿模塊具有相同的機械接口和電氣接口，可以根據需要快速組裝成不同構型的機械臂以滿足用戶的需求.末端可以連接不同的夾持或操作機構，如圖4所示為利用不同的關節模塊和連桿模塊組成的不同自由度的機械臂構型.

圖4 模塊化機械臂構型

2 機械臂運動學模塊化分析

設計的關節模塊通過不同組合可以形成不同自由度數及構型的機械臂，需要建立統一的模塊化運動學.利用魏延輝提出的構形平面匹配的思想［14-15］，對所研制的模塊化關節組裝成的各種構型機械臂的運動學模塊化進行了分析，并設計了運動學仿真平臺.最后以六自由度模塊化機械臂為例對運動學算法進行了求解和仿真驗證.

2.1 運動學建模

由于可重構模塊化機器人的構型和所選模塊的不確定性和多樣性，為了能夠快速獲得其運動學，希望能用相同形式的表達式表示不同的模塊.關節模塊的主要形式有移動關節模塊、回轉關節模塊和搖擺關節模塊，連桿模塊有平行式和垂直式.

模塊的統一表達方式為

式中:θ為回轉模塊的回轉角度，β為搖擺模塊的搖擺角度，β為搖擺模塊的連接長度，h為回轉模塊或連接模塊的連接長度，w為移動模塊的移動量．

通過基本模塊的統一表達方式，在已知模塊類型的情況下，即可建立機器人正運動學:

引入構形平面，每個構形平面由若干個搖擺模塊、若干個移動模塊、若干個連接模塊與一個回轉模塊組成.在無空間蔽障的條件下，一般2個構形平面進行匹配就能夠滿足機器人工作空間點的位姿要求;某些情況下，需要3個構型平面.經過構形平面的姿態匹配和位置匹配，關節角的求解就轉化成了平面內的運動學求解，可根據幾何關系求出各關節角的值.

2.2 運動學求解

以其中一種構型的六自由度機械臂(如圖5所示)為例來進行運動學的求解.

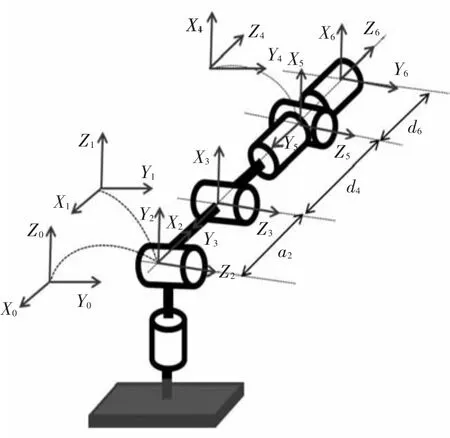
圖5 六自由度模塊化機械臂

該機械臂構型由3個回轉模塊和3個搖擺模塊組成，將各個模塊的參數代入式(1)得到各個模塊的數學模型，將其代入式(2)可得機械臂的正運動學:

其中:

逆運動學求解，已知機械臂末端位姿矩陣為

首先對機械臂進行構形平面姿態匹配，該構型的機械臂最多由兩個構形平面組成，設

則姿態匹配矩陣為

式中:θ1是關節1的回轉角度;θ'是構形平面一回轉關節的回轉角度，即關節4的回轉角度;β1+β2是構形平面1上各個搖擺關節的搖擺角度之和，即關節2和關節3回轉角度之和;θ″是構形平面2回轉關節的回轉角度，即關節6的回轉角度;β3是構形平面2上各個搖擺關節的搖擺角度之和，即關節5的回轉角度．經過構形平面姿態匹配可以求出θ1、(θ2+θ3)、θ4、θ5和θ6．

然后進行構形平面位置匹配，關鍵是確定構形平面一匹配點的空間坐標值，在經過構形平面的姿態匹配和位置匹配后，關節角的求解就轉化成了平面內的運動學求解，根據幾何關系求出關節角θ2和θ3的值，從而完成逆運動學求解．

2.3 運動學仿真與驗證

根據所設計的機械臂關節模塊和連桿模塊，基于MFC框架類和Open Inventor圖形庫，在VC++6.0開發平臺上開發一套適用于這種構型的三維仿真工具，如圖6所示.用戶可以按照需要從已有的模塊庫中選取所需的關節模塊和連桿模塊，以任意的連接順序組裝成不同自由度、不同構型的機械臂，并能快速獲得所組成的機械臂的正、逆運動學，以驗證對機械臂運動學模塊化建模以及正、逆運動學分析的正確性.

圖6 模塊化機械臂運動學仿真界面

以圖5所示構型的六自由度機械臂為例，給各個關節角以特殊的角度，利用所設計仿真工具得到機械臂末端的位置和姿態，根據實際機械臂的位姿判斷正運動學的正確性，結果如表1所示.通過驗證，正運動學解法是正確的.隨機給出機械臂末端的位置和姿態，利用所設計的仿真工具進行逆運動學求解，求得各個關節角的角度，再將這些角度代入正運動學得出末端位姿，與給出的位姿進行對比以驗證逆運動學解法的正確性，結果如表2所示，通過驗證，逆運動學解法是正確的.

表1 運動學正解驗證數據

表2 運動學逆解驗證數據

3 模塊化機械臂控制系統設計

由設計的關節模塊組成的機械臂的控制系統結構方案如圖7所示，采用基于工業以太網的開放式分布控制系統，主要由上位機、下位機、控制器、驅動器等組成，從上位機、主控計算機、運動控制器三層次控制機器人，各部分獨立運行，能夠適應各種模塊組成構型的機械臂控制.

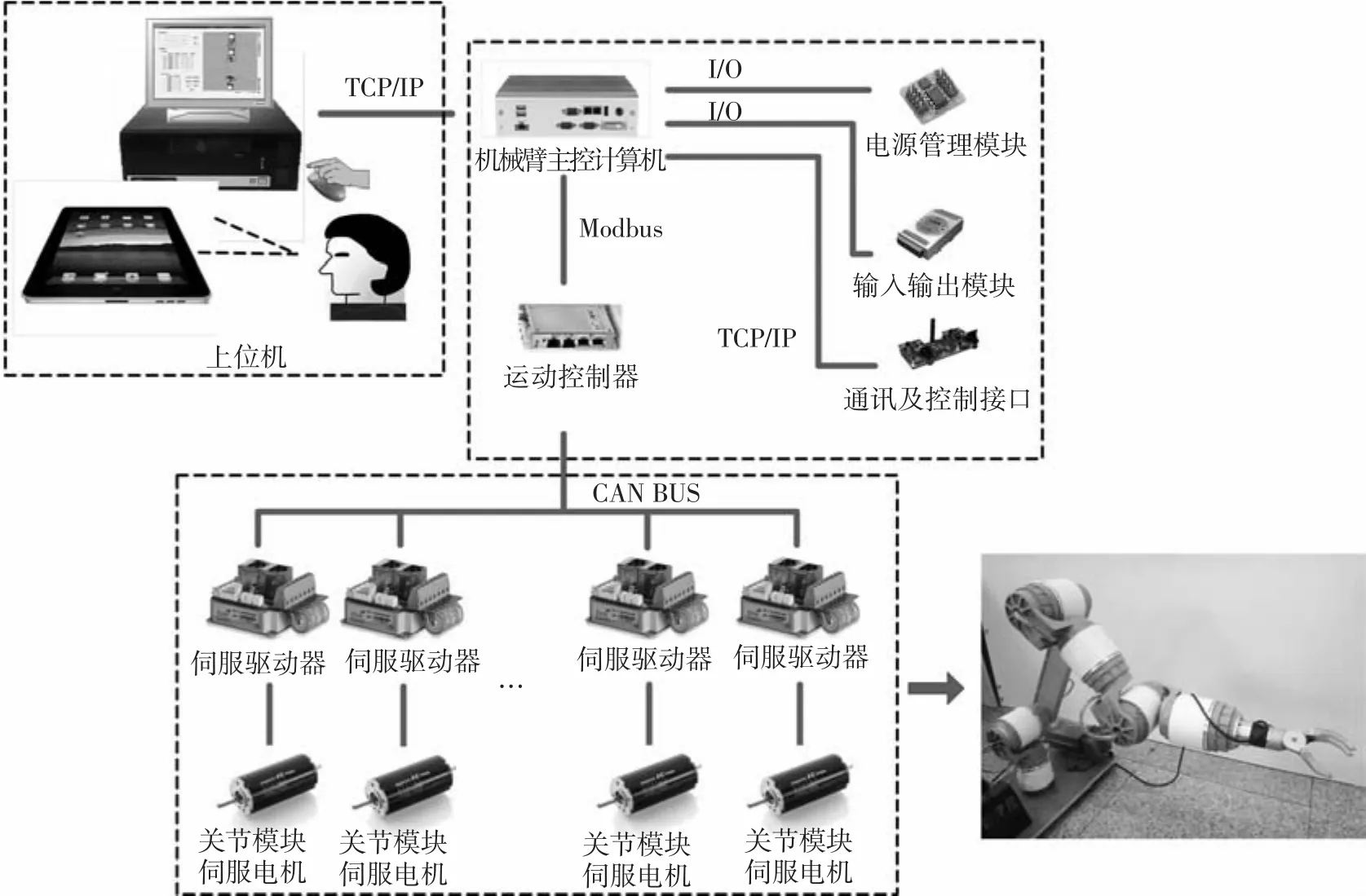
圖7 控制系統結構

上位機為操作者提供人機接口，根據環境和操作者的命令進行任務規劃，通過人機交互界面向下位機發送控制指令，并在線監控系統的運行情況.下位機負責將上位機的控制指令進行解析，經過運動學解算等將控制指令發送給控制器.控制器負責將從下位機接收到的控制指令發送給驅動模塊，并對反饋模塊的輸入信號進行實時采集和處理.驅動器獲得控制模塊的指令，對執行機構進行驅動.

用戶通過鼠標、鍵盤等操控上位機人機交互控制軟件，產生機械臂的控制命令，通過TCP/IP協議發送給主控計算機(下位機)，主控計算機接收指令并根據力矩傳感器反饋的信息，經運動學、力控制算法處理后生成控制命令，通過Modbus協議向控制器發送，控制器接收下位機指令控制電機運動，同時檢測編碼器的位置速度信息，并將電機的狀態反饋給下位機，從而實現整個系統的運動控制.

4 結 論

1)研制的新型機械臂關節模塊具有結構緊湊、體積小、重量輕、通用性好等特點，各個模塊具有相同的結構，能夠快速組裝成不同構型的機械臂.

2)采用構形平面思想對通用的模塊化運動學解法進行分析，并設計了模塊化運動學仿真平臺，以6自由度構型機械臂為例，驗證了運動學解法的可行性和正確性.

3)結合模塊化機械臂的特點，基于工業以太網建立開放式分布控制系統，從上位機、主控計算機、運動控制器三層次控制機器人，能夠適應各種構型的機械臂控制.

［1］PAREDIS C J J，BENJAMIN B H，KHOSLA P K.A rapidly deployable manipulator system［J］.Robotics and Autonomous Systems，1997，21(3):289-304.

［2］SCHMITZ D，KHOSLA P，KANADE T.The CMU reconfigurable modularmanipulatorsystem［C］//Proceedings of the International Symposium and Exposition on Robots.Piscataway:IEEE，1988:473-488.

［3］MATSUMARU T.Design and control of the modular robot system:TOMMS［C］//Proceedings of IEEE International Conference on Robotics and Automation.Piscataway:IEEE，1995:2125-2131.

［4］BAYRHAMMER E，KENNEL M，SCHMUCKER U，et al.Viro-Con:efficient deployment of modular robots［C］//Joint 41st International Symposium on Robotics and 6th German Conference on Robotics.Munich:VDE Conference Department，2010:759-764.

［5］魏延輝，朱延和，趙杰，等.基于柔性化工作的可重構機器人系統設計［J］.吉林大學學報，2008，38(2):

449-453.

［6］趙杰，魏延輝，蔡鶴皋.新型可重構機器人分布式控制方法的研究［J］.哈爾濱工業大學學報，2008，

40(1):39-42.

［7］崔馨丹，朱延河，王曉露，等.模塊化機器人的雙輸出CPG網絡調相運動控制［J］.哈爾濱工業大學學報，2013，45(7):47-52.

［8］LIU Xinjun，Chen Xiang，LI Zhidong.Modular design of typical rigid links in parallel kinematic machines:Classification and topology optimization［J］.Frontiers of Mechanical Engineering，2012，7(2):199-209.

［9］CHEN I M，GAO Yan.Closed-form inverse kinematics solver for reconfigurable robots［C］//Proceedings of the 2001 IEEE International Conference on Robotics＆Automation.Seoul:IEEE，2001:2395-2400.

［10］PAN Xinan，WANG Hongguang，JIANG Yong，et al.Research on kinematics of modular reconfigurable robots［C］//2011 IEEE International Conference on Cyber Technology in Automation，Control，and Intelligent Systems.Piscataway:IEEE，2011:91-96.

［11］TEJOMURTULA S，KAK S.Inverse kinematics in robotics using neural networks［J］. Information Sciences，1999，116(2):147-164.

［12］CHAPELLE F，BIDAUD P.Closed form solutions for inverse kinematics approximation of general 6R manipulators［J］.Mechanism and Machine Theory，2004，39(3):323-338.

［13］吳文強，管貽生，朱海飛，等.面向任務的可重構模塊化機器人構型設計［J］.哈爾濱工業大學學報，2014，

46(3):93-98.

［14］WEI Yanhui，ZHAO Jie，ZHU Yanhe，et al.Inverse kinematic research based on a new type of reconfigurable robot［J］.西安電子科技大學學報，2008，35(1):175-182.

［15］魏延輝，趙杰，高延濱，等.一種可重構機器人運動學求解方法［J］.哈爾濱工業大學學報，2010，42(1):

133-137.