非對稱環形桁架索網天線預張力設計解析算法

范葉森，李團結，馬小飛，李正軍

(1.西安空間無線電技術研究所，710100西安;2.西安電子科技大學 機電工程學院，710071西安)

隨著深空探測、遠程通訊、地球觀測等航天事業的發展，迫切需要發展大型空間可展開天線［1-4］.在眾多可展開天線的結構形式中，環形桁架索網天線因具有可折疊、質徑比小、收縮比高、熱穩定性優良等特點，成為國內外學者和工程技術人員研究的熱點［5-9］.

環形桁架空間索網天線結構設計的關鍵是合理配置索網中各段繩索的預張力，以使索網各節點穩定在理想的位置上，這是一個以“形”找“力”的過程［10-17］.如果繩索中的張力分布不合理，實際節點位置和理想節點位置就會有偏差，從而產生設計誤差［15-17］.在索網天線中，繩索單元的數量通常大于自由節點數量的3倍，索網天線預張力求解是一個多解的問題，理論上滿足索網結構平衡的預張力有無窮多組.為了保證索網結構的穩定性和抗干擾能力，人們提出了同一網面上的最大張力比(最大繩索張力與最小繩索張力之比)盡可能小的要求［9-17］.根據國內外的研制經驗［9-20］，合理的一組繩索預張力必須滿足使結構平衡和最大張力比盡可能小這項要求.

目前，常見的索網結構張力優化算法有以下幾種:極小范數法［17］、平衡矩陣奇異值分解算法［14］以及把有限元法［11］、力密度法［12，20］和智能優化算法結合進行繩索預張力優化的綜合算法［15］等.這些算法對推動空間索網結構設計技術的發展都起到了非常積極的作用，但這些算法必須通過大量的迭代運算才能得到最終的結果，并且用這些算法編寫程序也較繁瑣，應用存在一定難度.在工程上，為了減小收攏體積，副網的焦距通常大于主網的焦距，以縮小整個桁架的高度［16］.目前，有關環形桁架索網天線張力優化算法的研究對象多為主副網對稱的結構［16］.事實上，對稱結構是非對稱結構的一種特殊形式，研究非對稱結構能夠得到更為一般的結論.

為提高運算效率，方便工程技術人員應用，本文發展了一種適用于非對稱環形空間索網天線預張力設計的解析算法.只要給出主網繩索中的平均預張力，依次使用幾個線性代數公式即可得到完全滿足工程要求的繩索預張力.該算法不僅避免了迭代運算，而且在算法原理上不會產生設計誤差，因而具有較高的計算效率和計算精度.

1 計算模型

圖1所示為一個空間環形桁架索網天線計算模型［14，16］，該型天線主要由主網、副網、張力陣和環形桁架4部分構成.主網、副網和張力陣均由芳綸纖維繩索制作，環形桁架為碳纖維管材.主網和副網為拋物面，在主網上鋪設輕質金屬網，用于反射電磁波.

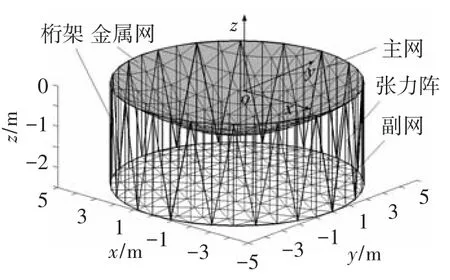
圖1 環形桁架索網天線計算模型

為便于計算，以環形桁架上環面中心為坐標原點，建立整個計算模型的總體坐標系o-xyz，z軸與環形桁架中心線平行．張力陣中的繩索都與z軸平行，主網與副網在xoy平面內的投影重合．將與主網節點i相連(投影重合)的副網節點稱為節點i的對應節點，并用表示該節點的編號;用繩索兩端節點的編號共同表示繩索的編號，并將副網繩索稱為主網繩索ij的對應繩索．如果分別用(xi，yi，zi)和(xi，yi，zi)表示主網節點i和副網節點的坐標，則xi=xi，yi=yi．為便于論述，將與桁架相連的索網節點作為固定節點處理，其他索網節點為自由節點．圖2為索網結構中任一繩索所受張力的示意圖．

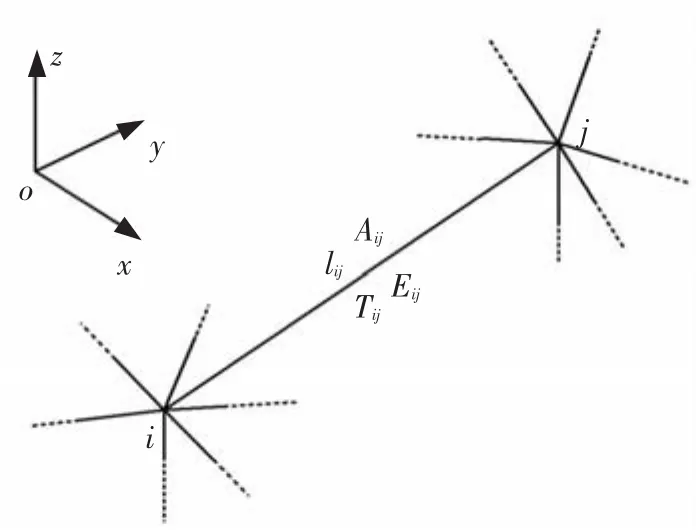
圖2 繩索張力示意圖

圖2中i、j為索網的任意兩個節點，Tij、Eij、Aij、lij分別為連接i、j兩個節點繩索ij的張力、彈性模量、截面積和兩節點之間張緊狀態的繩索長度，且lij滿足:

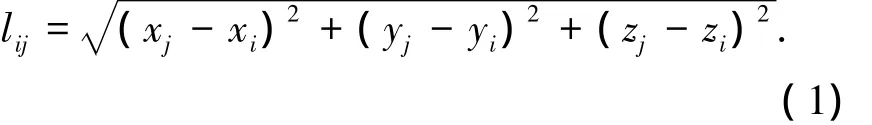
2 理論推導

2.1 索網預張力設計方法

2.1.1 主網預張力計算

為保持平衡，主網各自由節點在3個方向所受的合力都必須為零.太空環境是一個無重力環境，因此在空間索網結構預張力優化的過程中，無需考慮重力作用，作用在自由節點上的力只有繩索張力．因為主網繩索作用在各自由節點z向合力可由與該節點相連的張力陣繩索中的張力去平衡，主網繩索的預張力只要能夠使各節點在x向和y向平衡，主網中所有自由節點就都是穩定的．即只需要研究主網在xoy平面內投影的平衡問題，就能找到使主網平衡的繩索預張力．自由節點i在x向和y向的平衡方程為

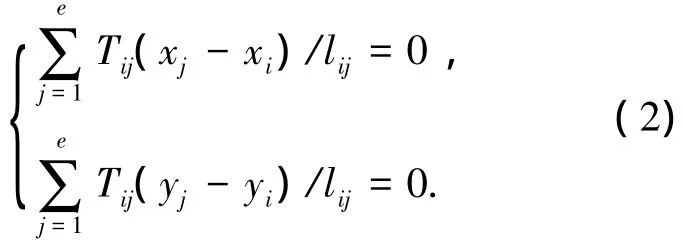
式中:j為與節點i相連的第j個節點編號，e為與節點i相連的主網繩索總數．則主網所有自由節點在x向和y向的平衡方程為

式中:U為力平衡方程的系數矩陣，T為主網繩索預張力組成的向量，ns為主網中自由節點，r為主網中繩索單元數．

基于平面索網結構預張力優化極小范數法［17］的基本原理，結合以上分析，可以得到一組主網預張力的優化解為

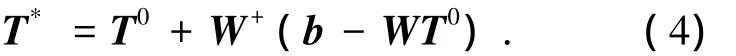
在用式(4)進行計算時，只要根據工程要求給定主網的平均預張力，就可以求出一組使主網在x向和y向平衡的預張力，而z向的平衡通過合理配置張力陣繩索預張力實現．

2.1.2 張力陣預張力計算

式(4)是式(3)的一組解，利用式(4)求出的繩索預張力必然可以使主網中的自由節點i在x向和y向平衡．為了使主網節點i處于平衡狀態，還必須合理配置與節點i相連的張力陣繩索預張力 Tii．為了讓節點 i在z向平衡，Tii必須與主網繩索作用在節點i上的z向合力相等，即

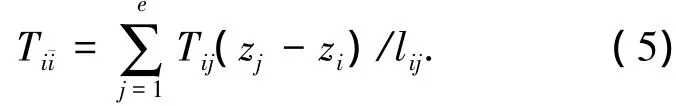
2.1.3 副網預張力計算

如果主網與副網是前后對稱的結構，即主網焦距f1與副網焦距f2相等，則副網繩索預張力與對應位置主網繩索預張力取相同值就能使副網處于穩定狀態．

如果主網與副網不是前后對稱的結構，即f1≠f2，則副網與主網繩索ij對應位置繩索ij中的預張力 Tij可取為

式中 lij為主網繩索 ij在副網對應繩索 ij的長度．

2.2 索網結構平衡論證

由以上論述可知，繩索預張力必須使索網各節點都穩定在理想位置.式(4)和式(5)求出的繩索預張力都是根據主網的靜力平衡方程得到的一組解，由式(4)和式(5)求出的繩索預張力一定能使主網各節點穩定在理想位置.如果根據式(6)求出的副網繩索預張力能使副網穩定在理想位置則整個索網系統就處于平衡狀態.

不失一般性，取與主網任一自由節點i對應的副網節點i進行分析．副網中節點i在x和y向合力為

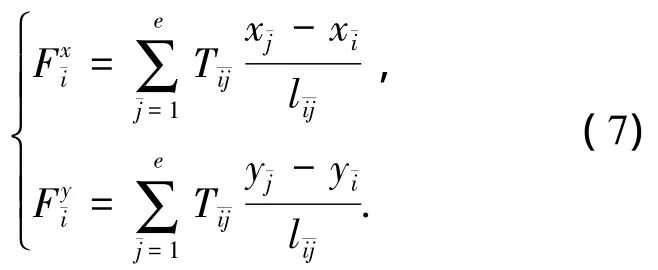
把 xi=xi，yi=yi和式(6)代入式(7)可得

把式(2)帶入式(8)，可得

由式(9)可知，副網在x和y向是平衡的．

因為主網和副網都為拋物面，可設主網的拋物面方程為

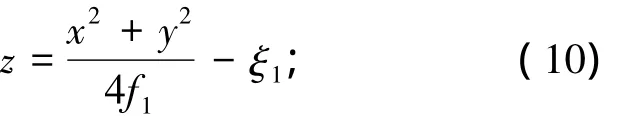
副網的拋物面方程為

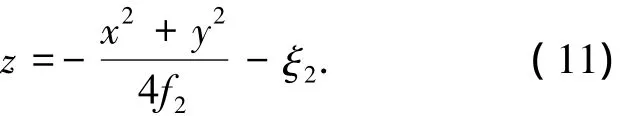
將式(5)帶入式(13)可得

由式(14)可知，副網作用在節點i上的z向合力與張力陣繩索作用在該節點上的力大小相等方向相反，是一對平衡力，因此該節點在z向也是平衡的．

綜上可知，使用式(4)～(6)計算得到的繩索預張力可使整個索網系統都處于平衡狀態，各節點都穩定在理想位置.即只需要根據設計要求，給出一個主網繩索預張力的平均值，就可以求出一組使主網平衡的繩索預張力，然后根據主網的縱向平衡方程，就可求出張力陣繩索張力;當求出一組主網的平衡預張力后，讓主網繩索中的預張力分別與特定的系數相乘，就可以得到一組使副網平衡的預張力.

2.3 繩索初始長度計算

繩索的初始長度是繩索裁剪的依據，為繩索在無應力狀態下的長度．在求出每段繩索ij的預張力Tij后，可求出繩索ij的初始長度為

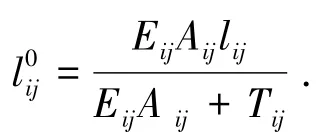
3 算例分析

為進一步驗證本文算法的正確性、可行性和有效性，便于將計算結果進行對比，下面對一個具體算例進行分析.

根據文獻［16-17］，選取圖1所示計算模型的結構參數，天線口徑10 m，前索網拋物面焦距f1=6 m，后索網拋物面焦距f2=40 m.為了用非線性有限元法對計算結果進行驗證，還需要補充一些結構參數.選取主網繩索預張力的平均值為20 N，直徑為1 mm，繩索的彈性模量為20 GPa，環形桁架高度為2.5 m.把采用本文所提算法計算得到的繩索預張力轉化為繩索初始應變后，將預張力優化結果導入ANSYS軟件進行非線性有限元分析，繩索單元為Link10，把各節點的理想位置作為各節點的初始位置，索網結構有限元模型如圖3所示.

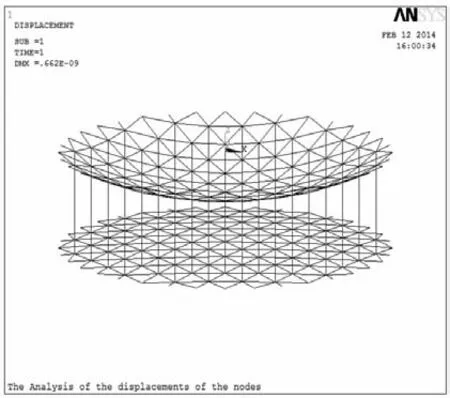
圖3 索網結構有限元模型

對于具體的工程來說，如果各節點位移都處在一個較小的范圍(1×10-6mm)內，就可以認為整個索網結構處于穩定狀態.經過ANSYS計算，整個索網結構各節點的最大位移為0.662×10-9mm，因此整個索網系統處于穩定狀態，采用本文所提算法得到的繩索預張力可以使索網各節點穩定在理想位置.

為進一步論述本文所提算法的可行性，把本文算法計算結果與其他算法的計算結果做一比較.當取主網的平均預張力為20 N時，采用本文算法計算得到的主網張力陣和副網的預張力最大和最小值如表1所示.

表1 預張力優化結果 N

計算出全部繩索的預張力后，即可以計算不同部位繩索預張力的最大張力比.文獻［16-17］都對圖1所示計算模型的預張力優化問題進行了研究，并且主網和副網的結構尺寸與本文所選取結構尺寸相同.文獻［16-17］及本文算法得到的繩索預張力的最大張力比如表2所示.

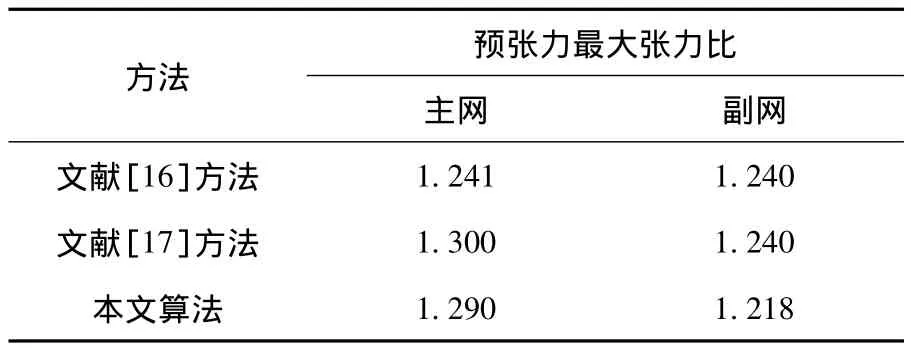
表2 不同算法得到的預張力的最大張力比

由表2可知，本文算法得到的計算結果全面優于文獻［17］的計算結果;副網預張力優化結果優于文獻［16］方法的計算結果，主網預張力的最大張力比略大于文獻［16］方法的計算結果，差值為3.95%.

文獻［14］采用平衡矩陣奇異值分解算法對一個前后對稱的索網天線預張力進行了優化計算，主、副網結構尺寸與本文所用計算模型主網尺寸相同，文獻［14］得到的主網預張力的最大張力比為1.38;對于這一模型，用本文算法得到主網預張力的最大張力比為1.29.本文所提算法得到的計算結果優于文獻［14］所提算法的計算結果.考慮到把力密度法、有限元法和智能優化算法(如遺傳算法)結合進行預張力優化的綜合算法會產生一定的設計誤差［10］，本文不再與這些綜合算法的計算結果進行對比.

綜上，本文的解析算法所得計算結果總體上優于或接近目前常見的幾種高精度空間索網結構預張力優化算法;同時，相對于其他算法，本文提出的解析算法避免了迭代，減小了編程工作量，提高了計算效率，更便于工程應用.采用matlab內部計時器進行計時，對圖1所示的計算模型進行一次預張力優化計算的時間為0.0491 s.

4 結 論

1)提出一種適用于非對稱環形桁架索網天線預張力設計的解析算法，并給出該算法的計算步驟，對于結構確定的環形桁架索網天線，只需給出主網的平均張力，就可以根據式(4)～(6)求出一組滿足設計要求的繩索預張力.

2)理論推導、數值仿真以及與其他算法的比較表明，本文所提算法正確、可行和有效，可用于對稱或非對稱環形索網天線繩索的預張力優化計算.

3)算法避免了常規算法中普遍存在的反復迭代求解的步驟，理論簡潔，具有較高的計算效率，便于工程應用.

［1］HIGUCHI K，KISHIMOTO N，MEGURO A，et al.Structure of high precision large deployable reflector for space VLBI［C］//50th AIAA/ASME/ASCE/AHS/ASC Structures， Structural Dynamics and Materials Conference.Palm Springs:AIAA Press，2009:AIAA 2009-2609.

［2］ORIKASA T，MIURA A，HIROYUKI T，et al.A Study of large reflector antenna mounted on communication satellite for satellite terrestrial mobile communication system［C］//31st AIAA International Communications Satellite Systems Conference.Florence:AIAA Press，2013:AIAA 2013-5649.

［3］TANAKA H.Surface error estimation and correction of a space antenna based on antenna gain analyses［J］.Acta Astronautica，2011，68:1062-1069.

［4］THOMAS W M.Historical perspectives on the development of deployable reflectors［C］//50th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Conference.Palm Springs:AIAA Press，2009:AIAA 2009-2605.

［5］SHI H，YANG B，THOMSON M，et al.A nonlinear dynamic model and free vibration analysis deployable mesh reflectors［C］//52nd AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics and Materials Conference.Denver:AIAA Press，2011:AIAA 2011-1999.

［6］SHI H，YANG B，THOMSON M，et al.Automatic surface mesh generation for design of space deployable mesh reflectors［C］//53rd AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics and Materials Conference.Honolulu:AIAA Press，2012:AIAA 2012-1840.

［7］楊東武，尤國強，保宏.拋物面索網天線的最佳型面設計方法［J］.機械工程學報，2011，47(19):123-128.

［8］SHI H，YANG B，FANG H.Offset-feed surface mesh generation for design of space deployable mesh reflectors［C］//14th AIAA Gossamer Spacecraft Forum.Boston:AIAA Press，2013:AIAA 2013-1526.

［9］YANG B，SHI H，THOMSON M，et al.Optimal design of initial surface profile of deployable mesh reflectors via static modeling and quadratic programming［C］//53rd AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics and Materials Conference.palm springs:AIAA Press，2009:AIAA 2009-2173.

［10］MA X，SONG Y，LI Z.Mesh reflector antennas:form finding analysis review ［C］//54th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Conference.Boston:AIAA Press，2013:AIAA 2013-1576.

［11］李團結，周懋花，段寶巖.可展天線的柔性索網結構找形分析方法［J］.宇航學報，2008，29(3):794-798.

［12］邊鵬飛.環形桁架可展開天線的找形與動力學分析［D］.西安，西安交通大學，2012:1-34.

［13］LI Tuanjie，JIANG Jie，DENG Hanqing，et al.Formfinding methods for deployable mesh reflector antennas［J］.Chinese Journal of Aeronautics，2013，26(5):1276-1282.

［14］李剛，關福玲.環形桁架展開天線索網的預拉力優化技術及工程應用［J］.固體力學學報，2006，27(專輯):174-179.

［15］GUAN Fuling，DAI Lu，XIA Meimeng.Pretension optimization and verification test of double-ring deployable cable net antenna based on improved PSO［J］.Aerospace Science and Technology，2014，32(1):19-25.

［16］楊東武，保宏.非對稱索網拋物面天線力平衡特性及預拉力設計［J］.機械工程學報，2009，45(8):308-312.

［17］楊東武.星載大型可展開索網天線結構設計與型面調整［D］.西安，西安電子科技大學，2010:55-80.

［18］MORTEROLLE S，MAURIN B，QUIRANT J，et al.Numerical form-finding of geotensoid tension truss for mesh reflector［J］.Acta Astronautica，2012，76:154-163.

［19］LIU W，LI D.Simple technique for form-finding and tension determining of cable-network antenna reflectors［J］.Journal of Spacecraft and Rockets，2013，50(2):479-481.

［20］CHU Zhengrong，DENG Zongquan，QI Xiaozhi，et al.Modeling and analysis of a large deployable antenna structure［J］.Acta Astronautica，2014，95:51-60.