深海履帶車的路徑跟蹤控制算法

韓慶玨，劉少軍

?

深海履帶車的路徑跟蹤控制算法

韓慶玨，劉少軍

(中南大學 機電工程學院，深海礦產資源開發利用技術國家重點實驗室，湖南 長沙，410083)

建立深海履帶車運動學和路徑偏差模型，并針對履帶車在工作環境中出現的路徑偏差問題提出一種新的路徑跟蹤算法。基于履帶車的行走動力約束，路徑跟蹤算法中引入線速度和角速度中間變量，避免了由于履帶車驅動輪角速度突然變化所導致的系統失穩。同時，為提高系統的響應時間，算法中增加與PID控制類似的比例環節，利用李雅普諾夫法證明控制系統的穩定性，并對深海采礦2種典型期望工作路徑的路徑跟蹤進行仿真。研究結果表明：所提出的新的路徑跟蹤算法具有良好的快速性和穩定性，能夠滿足深海采礦履帶車的行走控制要求，保證履帶車良好的行走性能。

深海；履帶車；路徑跟蹤；算法

對于深海6 km多金屬結核及鈷結殼采礦領域而言，世界各國相繼研制出包含海底履帶式采礦車的深海采礦系統[1]。近年來，深海履帶車系統作為整個深海采礦系統的核心之一成為各國研究的熱點。由于受到海底極其稀軟底質特點以及海底洋流等環境因素的影響，深海履帶式采礦車的行走控制較困難。為使采礦車能準確按照預定開采路徑進行海底作業，采用合理高效的路徑跟蹤控制算法顯得尤為關鍵。Herber 等[2]對非線性移動機器人的穩定性進行了研究。Endo等[3]利用測距法對小型履帶車輛進行路徑跟蹤控制研究；Keiji等[4]在考慮打滑的情況下利用陀螺儀提高了測距法路徑跟蹤控制的準確性；Zhou等[5]利用非線參數估計法提出了基于濾波器的跟蹤算法。徐俊艷等[6]提出了雙曲正切特征曲線路徑跟蹤算法，并用李雅普諾夫方法證明了系統的全局穩定性。但是，這些研究主要針對運動環境相對簡單的陸用車輛。深海履帶式采礦車行走的環境極其復雜，由于受到海底稀軟底質以及海底洋流的影響，其動力學和運動學是研究的熱點。Schulte等[7]通過理論分析和大量實驗對深海履帶式采礦車動力學特性進行了研究。Yeu等[8]設計了PID和增強型PD路徑跟蹤控制器，并通過對2種控制效果的仿真對比，對軟底質環境下履帶車的路徑跟蹤控制進行了研究；之后，Yeu等[9?10]又提出向量跟蹤以及LOS視線路徑跟蹤控制算法，并通過實驗驗證了算法的可行性。Wang等[11]利用模糊控制理論，提出了連續狀態反饋的有限時間深海采礦車路徑跟蹤控制算法。李力等[12]建立了深海履帶式采礦車液壓動力系統模型，利用模糊算法對其運動進行了控制。Dai等[13]綜合考慮了軟底質及洋流的影響，提出了PID算法，實現了對海底履帶車的路徑跟蹤控制。然而，上述研究將深海稀軟底質作為影響路徑跟蹤控制的重要因素，但忽略了采礦車驅動系統自身固有的動力約束對路徑跟蹤問題的影響。本文作者在深海履帶車運動學模型的基礎上，提出一種新的路徑跟蹤算法。算法中引入中間線速度和角速度變量以滿足履帶車輛實際驅動系統的動力約束。通過對2種典型的采礦路徑的仿真分析，得到了比較好的控制效果。

1 深海履帶車運動學模型

深海履帶車的行走裝置是由左、右2條履帶構成，其行走動力由履帶驅動輪提供。通過調整左、右履帶驅動輪的轉速可以實現履帶車直行和轉彎過程。考慮到深海履帶車的行走環境，其自由度變化較少，固履帶車可以簡化為1個二維的車輛運動學問題。在全局坐標系中，選取固定在履帶車上的坐標系統來對履帶車的運動過程進行描述，如圖1所示。

圖1 履帶車運動學模型

圖中：點為履帶車運動瞬心；為履帶車質量中心；為履帶車左右履帶的中心距；為側向打滑角；C履帶車的方向角；C為履帶車的角速度；i和o分別為內、外側履帶的線速度。在不考慮縱向打滑的情況下，

式中：為履帶轉動半徑；i和o分別為內、外側履帶驅動輪角速度。由此，可以得到履帶車的線速度和角速度為：

由圖1中的幾何關系可知

對于執行深海采礦作業的履帶車，由于其行走速度較小(約0.5 m/s)，同時其所受的側向摩擦力很大，因此，假定在履帶車轉彎過程中由向心力引起的側向打滑率為0，即圖中=0°。則履帶車的運動學方程為：

2 深海履帶車路徑偏差模型

對于深海采礦，為了提高開采效率，在履帶車進行開采作業前其開采路徑已經基本確定。但在實際采礦過程中，由于布放偏差、海底軟底質產生打滑、海底洋流以及與履帶車車相連的軟管等作用的影響，深海履帶車在作業過程中與期望開采路徑將會存在一定偏差，其路徑偏差模型可用圖2表示。圖2中：為預定路徑；d(d，d，d)為履帶車期望位置坐標；C(C，C，C)為履帶車當前位置坐標。定義履帶車e為當前位置與期望位置的偏差，則e可以通過下式計算得到：

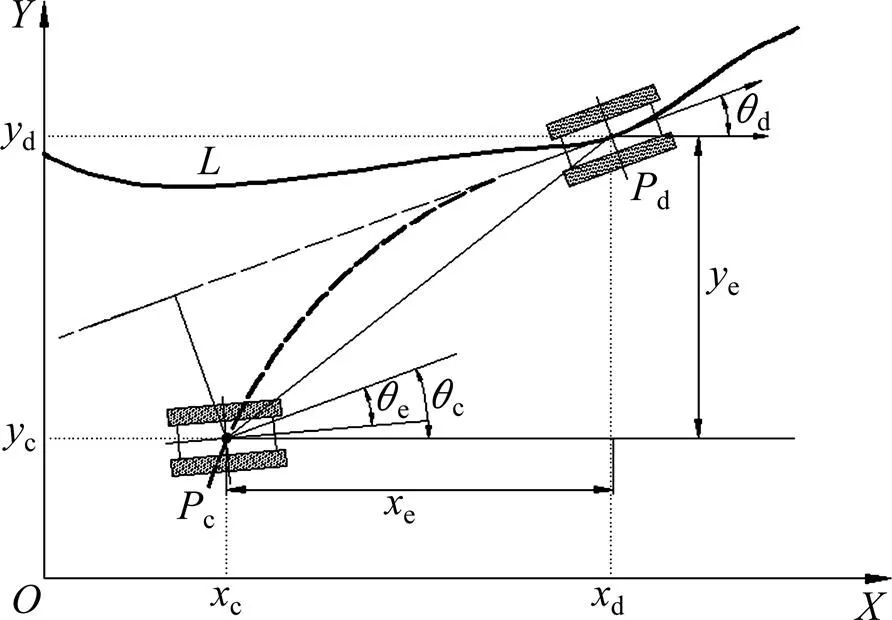
圖2 履帶車路徑偏差模型

同時可以得到路徑偏差的導數為

路徑跟蹤控制問題就是使履帶車系統在任意初始位置誤差下，確定履帶車的輸入控制和使得(e，e，e)T有界且lim→∞||(e，e，e)T||=0。

3 履帶車行走動力約束

深海履帶車在運動過程中，由于自身動力系統性能條件的約束，履帶驅動輪的角速度不能隨意調整。在控制履帶車進行路徑跟蹤過程中，應該盡量避免驅動輪角速度突然變化情況的發生，否則會導致系統的機械沖擊或履帶嚴重打滑，這些都不利于履帶車的系統穩定。

設履帶車驅動輪角加速度的最大值為max，則履帶車行走動力約束條件為

同時，由式(1)~(3)可得

將式(11)中2個式子相加并取導可得

式中：C和C分別為驅動輪的線加速度和角加速度。由式(12)可以看出：驅動輪的角加速度和線加速度約束條件耦合在一起，將最大角加速度平分可以得到獨立的角加速度和線加速度約束條件為：

4 路徑跟蹤算法

由履帶車動力約束條件可知，所設計的路徑跟蹤算法不能使履帶驅動輪角加速度超出其最大值；同時，為了保證履帶車系統的穩定性，驅動輪的角速度也不應有突然變化。為了滿足上述2個條件，在算法中引入驅動輪線速度和角速度判斷中間變量j和j：

式中：1，2，3和4為控制系數，均為正值；sgn()為符號函數。在一定的采樣周期Δ內，可以將線速度和角速度中間變量轉換為加速度中間變量，即

由于式(16)中的加速度參考值是基于動力約束的，所以，將此參考值與集礦機最大線加速度和角加速度進行比較，取較小值作為最終履帶車路徑跟蹤控制輸入，得到路徑跟蹤控制算法為：

在采樣周期Δ內，對履帶車驅動輪的線速度和角速度進行離散化可以得到路徑跟蹤的控制方程為

此路徑跟蹤算法的思想來源于傳統的PID控制。傳統PID控制中，比例環節對于系統響應的快速性有所改善，所以應予以保留；另外，履帶車的動力約束與路徑偏差有關，所以，在中間變量中引入max|e|和max|e|。

5 算法穩定性證明

深海履帶車路徑跟蹤控制系統的穩定性要求履帶車無論以任何位置為初始條件，系統最終都能跟蹤到期望路徑上，即系統具有收斂性。選取李雅普諾夫函數

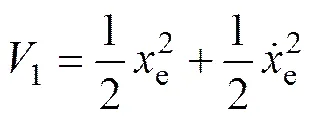
對上式取導得

由式(15)可知：

其中：d為履帶車期望位置處的線加速度。將式(21)和(22)代入式(20)得

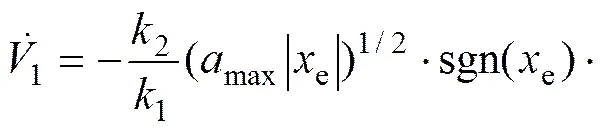
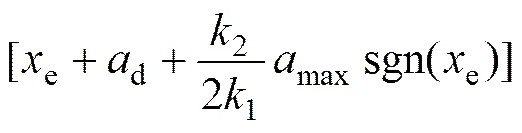
因為1和2均為正值，，且當時，。所以，當時，，即系統漸進穩定。對于深海履帶車方向角的系統穩定性可以利用同樣的方法得以 證明。

6 路徑跟蹤仿真

6.1 深海采礦預定路徑

對于深海采礦領域，目前國際上普遍提出的深海采集路徑為“S”型路徑。為了保證履帶車海底作業過程安全、高效與環保，韓慶玨等[14]提出了2種新的采集路徑，如圖3所示。

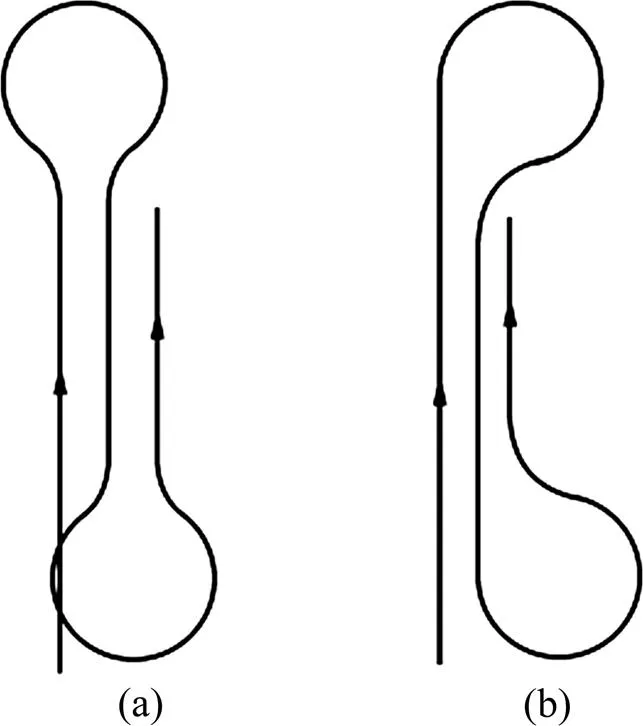
(a) 路徑a；(b) 路徑b

此2種采集路徑(a和b)描述如下。采集路徑a示意圖見圖4。圖4中=21.8 m。履帶車按采集路徑a行走時，需要進行4次調速，如圖4中曲線①~④所示。第1次調速使履帶車由直線行駛轉變為弧線行駛。履帶車轉向行駛角度=55.97°后進行第2次調速，在轉向行駛角度=291.94°時進行第3次調速。再進行轉向行駛角度=55.97°后進行第4次調速，最終沿直線行駛。履帶車經過此4次調速后，保證2條直線行駛軌跡間距等于履帶車的寬度 5.2 m。采集路徑b見圖5。

圖4 采集路徑a示意圖

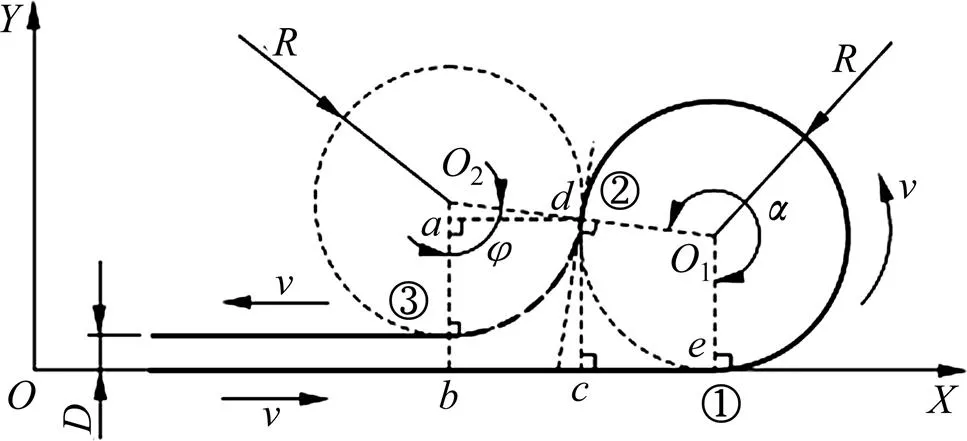
圖5 采集路徑b示意圖

對于采集路徑b，履帶車經歷3次調速，其中，2次轉向行駛角分別為=83.15°，=263.15°，圓弧軌跡半徑=21.8 m，2條直線軌跡間距=5.2 m。

6.2 仿真分析

為了驗證本文所提出的路徑跟蹤算法的有效性，分別對2種采集路徑進行仿真，仿真參數如表1所示。

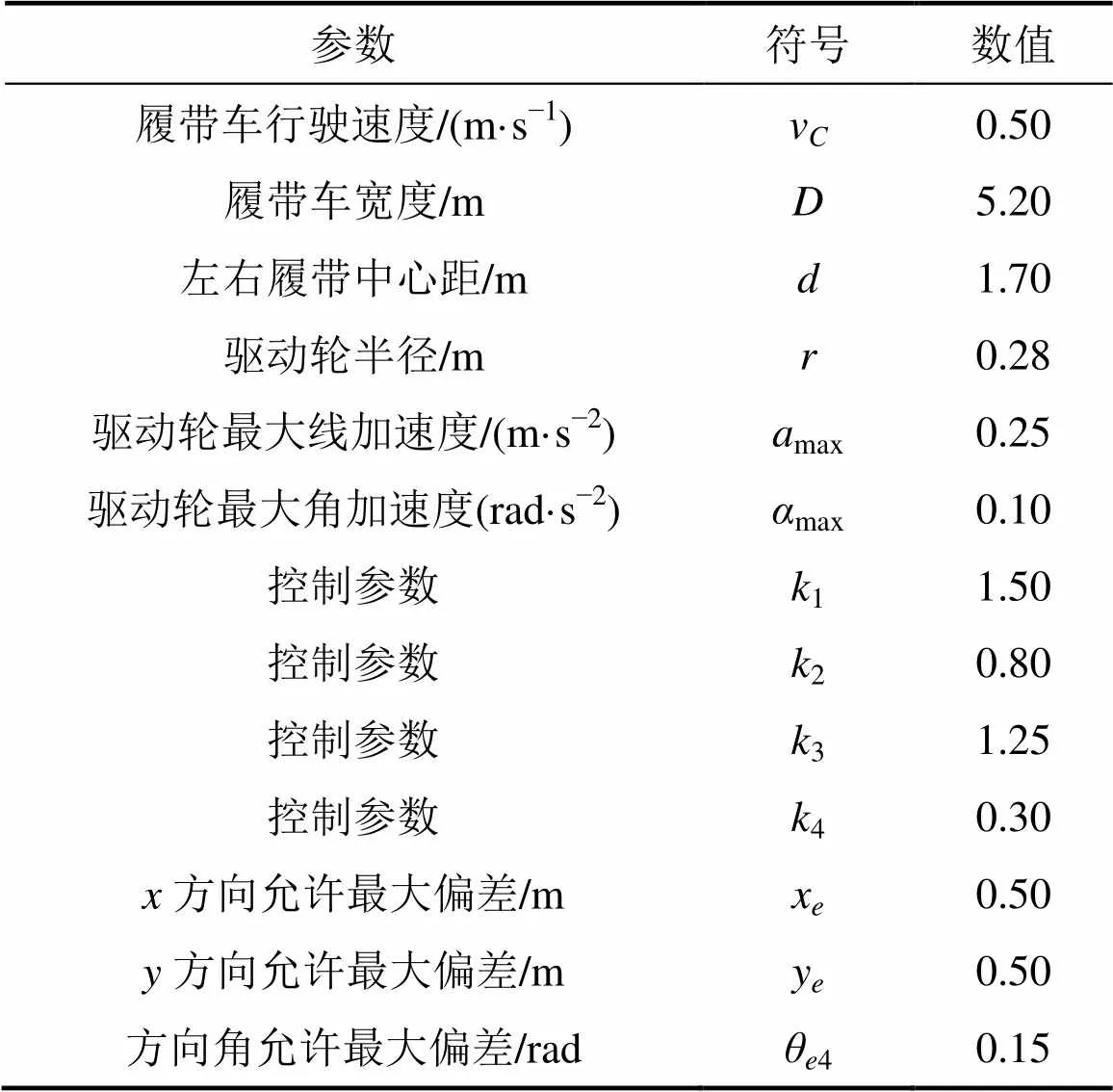
表1 仿真環境參數

2種采集路徑的起始位置為(0?0?0)。為了使仿真更具一般性，跟蹤采集路徑a的仿真中，設定履帶車的初始位置為(0，?5，0)，屬于小偏差路徑跟蹤；而跟蹤采集路徑b的仿真中，初始位置偏差設定為(?10，?10，0)，屬于大偏差路徑跟蹤。

圖6(a)所示為履帶車實際行走路線與預定路線仿真對比圖。從圖6(a)可以看出：仿真開始時履帶車初始位置偏差為5 m；履帶車自啟動后，逐漸朝預定路徑方向和位置靠近，水平方向約行走10 m后行駛在期望路徑上，此后履帶車實際行走路徑始終與預定路徑吻合，說明路徑跟蹤效果良好。

圖6(b)~(d)所示分別為路徑跟蹤過程中履帶車橫向、縱向以及方向角偏差曲線。從圖6(b)可以看出：履帶車啟動時橫向位置偏差為0，隨后偏差出現波動，這是履帶車跟蹤過程中不斷調整行走速度所致；10 s后橫向位置偏差穩定在0處，說明控制算法在橫向位置具有良好的快速性和穩定性。

圖6(c)所示為縱向偏差曲線。從圖6(c)可以看出：履帶車啟動時縱向偏差為5 m，隨后偏差迅速減小；經過10 s左右，縱向偏差穩定在0處，說明此時履帶車已沿預定路徑行走；但在200~265 s以及480~510 s期間，縱向偏差存在一定波動，波動范圍為±0.2 m。這是由于此時履帶車處于轉彎調速階段，速度的改變導致跟蹤誤差再次出現。由于偏差波動范圍較小，在誤差允許范圍內，故可以接受。

圖6(d)所示為方向角偏差曲線，其變化規律與縱向偏差一致。同樣在200~265 s以及480~510 s期間，由于履帶車轉彎調速，方向角偏差出現波動，波動范圍為±0.1 rad，在誤差允許范圍內，可以接受。

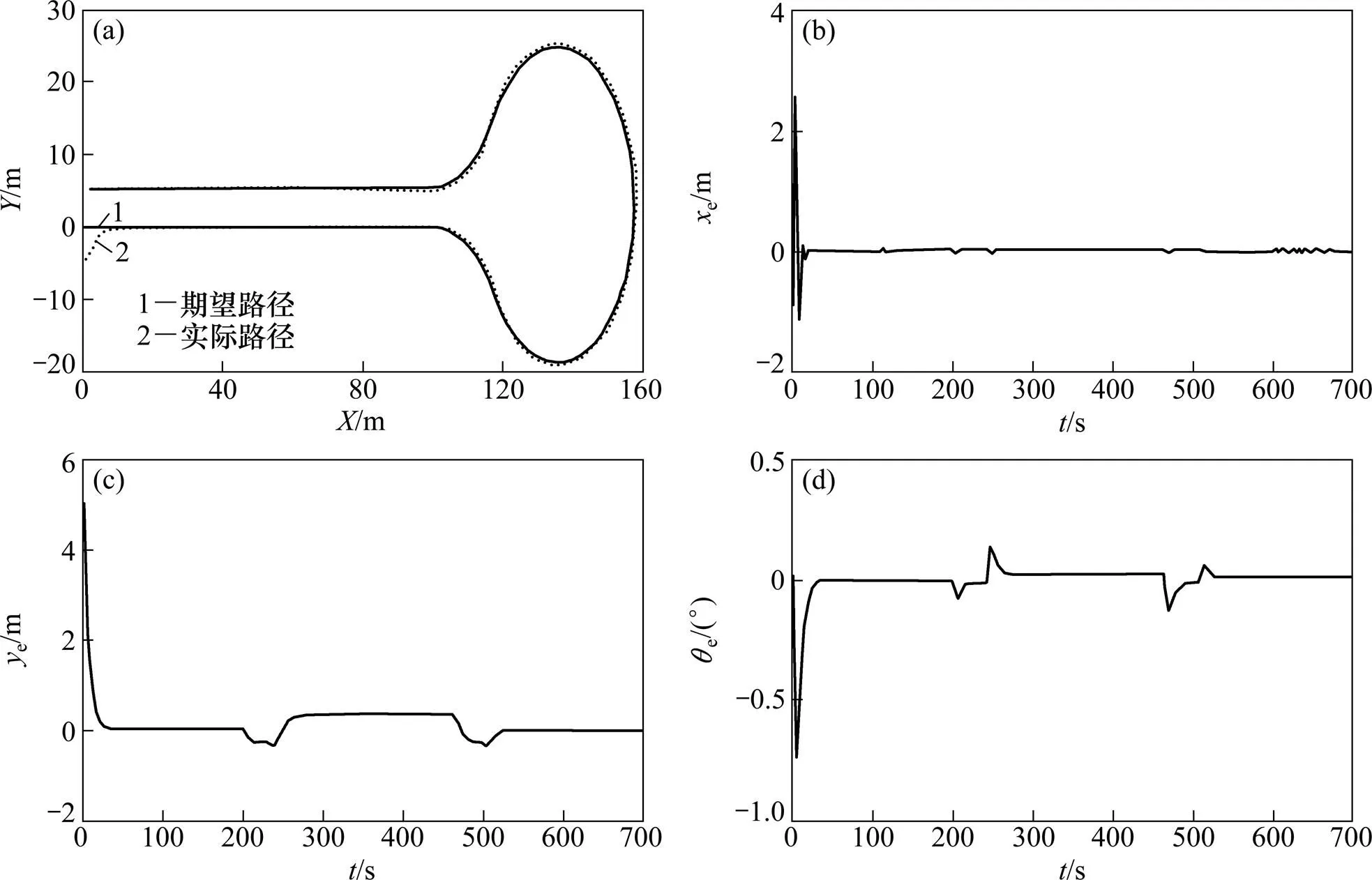
(a) 履帶車跟蹤預定路徑仿真圖；(b) 橫向偏差曲線；(c) 縱向偏差曲線； (d) 方向角偏差曲線

綜合以上對路徑跟蹤過程橫向、縱向以及方向角偏差的分析可知：在采集路徑a情況下，所提出的控制策略可以滿足履帶車路徑跟蹤要求，控制算法具有良好穩定性。

圖7(a)所示為履帶車實際行走路線與預定路線仿真對比圖。從圖7(a)可以看出：仿真開始時履帶車初始位置橫向、縱向偏差均為10 m，屬于大偏差范圍；履帶車自啟動后，迅速朝預定路徑方向和位置靠近，水平方向約行走25 m后行駛在期望路徑上，此后履帶車實際行走路徑始終與預定路徑吻合，說明路徑跟蹤效果良好。

圖7(b)~(d)所示為路徑跟蹤過程中履帶車橫向、縱向以及方向角偏差曲線。從圖7(b)可以看出：履帶車啟動時橫向位置偏差為10 m，隨后偏差迅速減小；約經過10 s后，偏差減小并穩定在0處。

圖7(c)所示為縱向偏差曲線。圖7(c)可以看出：履帶車啟動時縱向偏差為10 m，隨后偏差迅速減小并出現一定波動。其原因是在大偏差情況下為保證路徑跟蹤的快速性，履帶車調速。偏差經過15 s后減小并穩定在0處。

圖7(d)所示為方向角偏差曲線。從圖7(d)可見：其初始偏差為0°，隨后突然增大后迅速減小，大約在15 s附近減小并穩定在0°處。這說明履帶車啟動時與預定路徑方向一致。隨著路徑跟蹤過程履帶車轉彎，導致方向角偏差增大。同時方向角偏差在200~400 s，偏差為0.1 rad；在400~460 s，偏差為?0.1 rad。這說明在采集路徑(b)的轉彎過程，履帶車方向角偏差存在一定誤差，由于誤差屬可接受范圍，故整體方向角偏差控制效果良好。

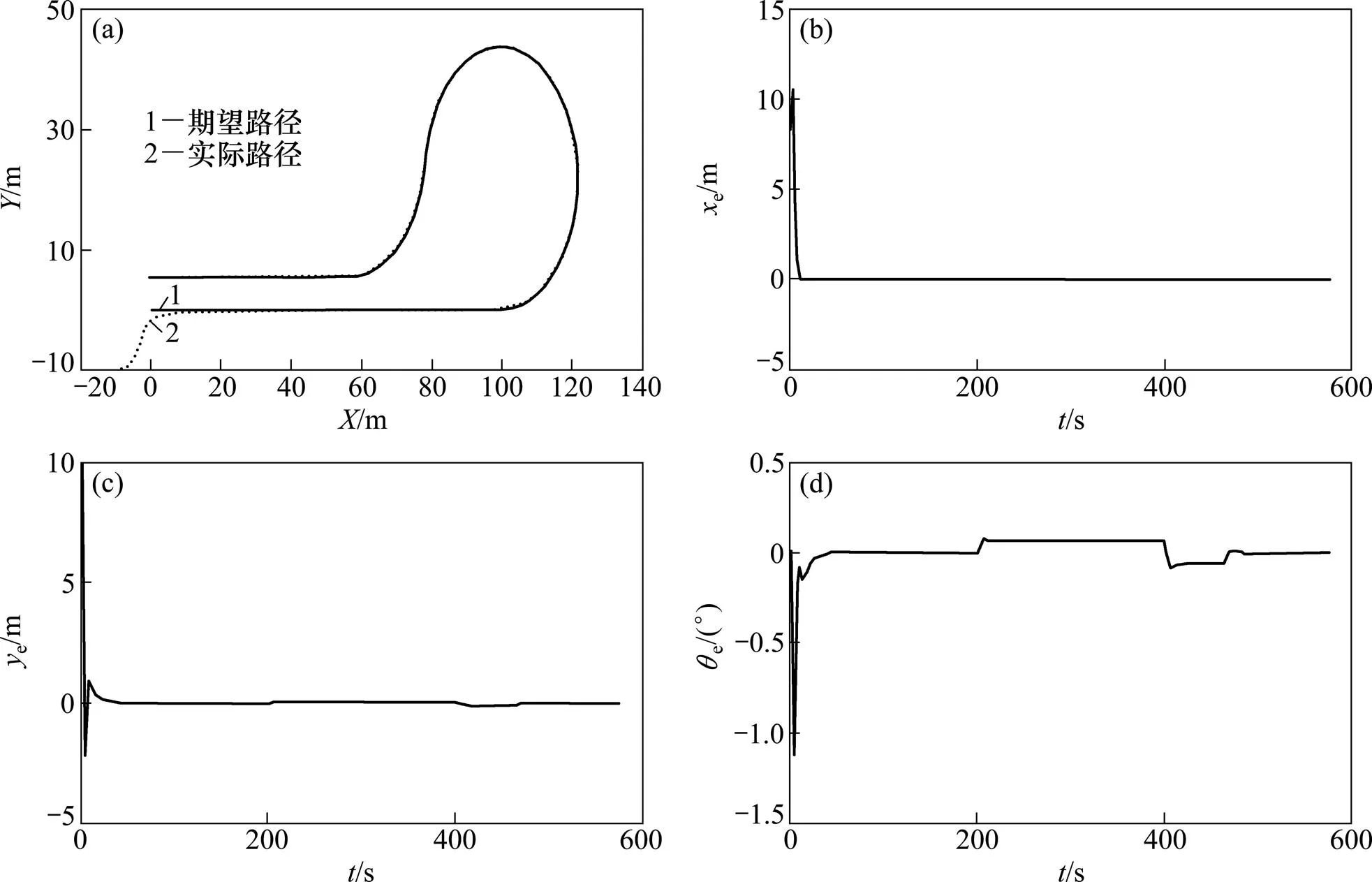
(a) 履帶車跟蹤預定路徑仿真圖；(b) 橫向偏差曲線；(c) 縱向偏差曲線；(d) 方向角偏差曲線

綜合以上對采集路徑b時路徑跟蹤過程橫向、縱向以及方向角偏差的分析可知：所提出的控制策略可以滿足履帶車路徑跟蹤要求，控制算法具有良好穩 定性。

綜合以上仿真結果可知：對于深海采礦不同期望采集路徑，本文所提出的路徑跟蹤算法能使履帶車快速有效地跟蹤期望采集路徑，跟蹤過程雖有波動，但仍在可接受范圍內。故算法能夠滿足深海采礦履帶車的行走控制要求，保證了履帶車良好的行走性能。

7 結論

1) 建立了完整的深海履帶車運動學模型和路徑偏差模型，并提出了履帶車動力約束條件，為深海履帶車路徑跟蹤提供了依據。

2) 基于深海履帶車動力約束條件，提出一種新的路徑跟蹤控制算法，算法中引入速度中間變量，保證了系統的動力要求。運用李雅普諾夫方法證明了算法的穩定性。

3) 針對深海采礦2種不同期望采集路徑，對路徑跟蹤控制進行仿真，仿真結果滿足路徑跟蹤控制要求，保證了深海履帶車行走的準確性。

下一步將著重于路徑跟蹤控制實驗研究。

[1] 戴瑜. 履帶式集礦機海底行走的單剛體建模研究與仿真分析[D]. 長沙: 中南大學機電工程學院, 2010: 1?10.
DAI Yu. The modeling research and simulation analysis on the single-rigid-body of tracked miner moving on the seafloor[D]. Changsha: Central South University. School of Mechanical and Electrical Engineering, 2010: 1?10.

[2] Herber G, Kostas J. Discontinuous backstepping for stabilization of nonholonomic mobile robots[C]//Proceedings of the IEEE International Conference on Robotics and Automation. Washington DC, 2002: 3948?3953.

[3] Endo D, Okada Y, Keiji N, et al. Path following control for tracked vehicles based on slip-compensation odometry[C]// Proceedings of the International Conference on Intelligent Robots and Systems. San Diego, USA, 2007: 2871?2876.

[4] Keiji N, Endo D, Yoshida K. Improvement of the odometry accuracy of a crawler vehicle with consideration of slippage[C]//Proceedings of International Conference on Robotics and Automation. Roma, Italy, 2007: 2752?2757.

[5] ZHOU Bo, HAN Jianda. Nonlinear estimation methods for autonomous tracked vehicle with slip[J]. Chinese Journal of Mechanical Engineering, 2007, 20(4): 1?7.

[6] 徐俊艷, 張培仁. 非完整輪式移動機器人軌跡跟蹤控制研究[J]. 中國科學技術大學學報, 2004, 34(3): 376?380.
XU Junyan, ZHANG Peiren. Research on trajectory tracking control of nonholonomic wheeled mobile robots[J]. Journal of University of Science and Technology of China, 2004, 34(3): 376?380.

[7] Schulte E, Handschuh R, Schwarz W. Transferability of soil mechanical parameters to traction potential calculation of a tracked vehicle[C]//International Society of Offshore and Polar Engineers. Proceedings of the 5th ISOPE Ocean Mining Symposium. Tsukuba, Japan: ISOPE, 2003: 123?131.

[8] Yeu T K, Hong S, Kim H W. Path tracking control of tracked vehicle on soft cohesive soil[C]//Proceedings of the Sixth ISOPE Ocean Mining Symposium. Changsha, China, 2005: 168?173.

[9] Yeu T K, Park S J, Hong S. Path tracking using vector pursuit algorithm for tracked vehicles driving on the soft cohesive soil[C]//Proceedings of SICE-ICASE International Joint Conference. Busan, Korea, 2006: 2781?2786.

[10] Hong S, Choi J S, Kim H Y, et al. A path tracking control algorithm for underwater mining vehicles[J]. Journal of Mechanical Science and Technology, 2009, 23(8): 2030?2037.

[11] WANG Suiping, GUI Weihua, ZHANG Tao, et al. Fuzzy and predictive control on the deep-sea vehicle[C]//Proceedings of the Sixth ISOPE Ocean Mining Symposium. Changsha, China, 2005: 181?186.

[12] 李力, 鄒興龍. 海底機器人自動跟蹤預定開采路徑[J]. 機械工程學報, 2007, 43(1): 152?157.
LI Li, ZOU Xinglong. Seafloor robots control on tracking automatically planning mining paths[J]. Chinese Journal of Mechanical Engineering, 2007, 43(1): 152?157.

[13] DAI Yu, LIU Shaojun. Theoretical design and dynamic simulation of new mining paths of tracked miner on deep seafloor[J]. Journal of Central South University, 2013, 20(4): 918?923.

[14] 韓慶玨, 劉少軍, 戴瑜, 等. 水下履帶式采礦車作業環境下的動力學分析及路徑跟蹤控制[J]. 中南大學學報(自然科學版), 2011, 42(2): 307?312.
HAN Qingjue, LIU Shaojun, DAI Yu. Dynamic analysis and path tracking control of tracked underwater miner in working condition[J]. Journal of Central South University (Science and Technology), 2011, 42(2): 307?312.

Path tracking control algorithm of the deep sea tracked vehicle

HAN Qingjue, LIU Shaojun

(National Key Laboratory of Development and Utilization of Deep-Sea Mineral Resource,School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

The kinematic and position error model of the deep sea tracked vehicle was established, and a new path tracking control algorithm was proposed to solve the path error problem of tracked vehicle during working. Based on the dynamic constraints, two intermediate variables were introduced in the control algorithm to avoid the systematic instability due to abrupt change in angular velocity of the vehicle sprocket. To improve the response time of the system, a proportional element was introduced in the algorithm. Meanwhile, the stability of the control system was proved using Lyapunov method, and a series of simulations of tracking two typical deep sea mining desired paths were carried out. The results show that the suggested algorithm is valid and can meet the control requirement; therefore, the walking performance of the tracked vehicle is ensured.

deep sea; tracked vehicle; path tracking; algorithm

TP242

A

1672?7207(2015)02?0472?07

2014?03?10；

2014?05?21

國家自然科學基金資助項目(51074179)；國家高技術研究發展計劃(863計劃)項目(2012AA091201)(Project (51074179) supported by the National Natural Science Foundation of China; Project (2012AA091201) supported by National High Technology Research and Development Program of China (863 Program))

韓慶玨，博士研究生，從事海底履帶采礦車行走控制研究；E-mail：qingjuehan@yahoo.com.cn

10.11817/j.issn.1672-7207.2015.02.014

(編輯 陳燦華)