基于多準則的組合預測模型權重研究及其應用

黃仁東，張海彬，楊志輝，周揚，張攀

?

基于多準則的組合預測模型權重研究及其應用

黃仁東1，張海彬1，楊志輝2，周揚1，張攀1

(1. 中南大學資源與安全工程學院，湖南長沙，410083；2. 中南大學冶金與環境學院，湖南長沙，410083)

針對傳統組合預測模型大多是通過建立單一準則方程進行優化，而沒有更好地考慮各單一模型之間互支持信息帶來的不確定性問題，建立基于多準則的組合預測模型權重確定算法。首先，通過建立區間數模型構建樣本區間距離并進行相關折算歸一化生成樣本的基本概率分布BPA(basic probability assignment)，作為單一預測模型的初級權重；然后，通過對D-S證據理論進行改進，建立證據可信度、證據精度和證據自沖突系數3個準則分別用于評價單一模型自身精度及其之間互相支持信息，通過對3個準則排序得到綜合排序值作為單一模型初級權重的權重調整系數；最后，綜合多時刻數據歸一化后確定單一模型的最終權重用于組合預測。研究結果表明：經過權重調整后的組合預測精度得到顯著提高，且經過調整系數調整后的不變權組合預測模型最優。

組合預測；證據理論；權重調整系數；可信度；證據精度；自沖突系數

預測是隨著社會發展而產生的，隨著人們對生產和生活要求的提高，傳統的單一預測模型自身存在的局限性顯得愈明顯。任何事物通常都是與周圍多種事物相互影響、相互制約的，而傳統的單一預測模型通常是在一定的假設條件下進行，這也就使得單一模型不能全面反映事物的信息。信息的缺失造成預測結果出現誤差，而這些誤差常常會給問題決策帶來嚴重的影響。為了解決單一模型誤差大的問題，Bates等[1]提出將多種單一模型結合起來的組合預測模型。組合預測方法是通過建立多種不同的單一預測模型，然后通過對各單一模型的預測結果進行一定加權組合得到最終預測結果。組合預測模型的研究重點在于單一模型權重的確定，目前大多是通過建立一定的目標準則而對組合模型進行優化確定權重。不同的準則可以得到不同的權重分配結果。然而，不同的準則都存在相應的缺陷，如預測誤差平方和準則作為判定模型預測精度的重要指標常常會因異常數據造成較大的偏差。針對不確定性誤差問題，出現了多種理論如證據理論、灰色理論、模糊理論、粗糙集理論等[2]。其中，證據理論由于滿足比概率論更弱的先驗概率要求，在模式識別、決策分析以及趨勢分析等多源信息融合領域得到廣泛應用。而傳統的證據理論在確定組合預測權重時通常是通過目標準則計算權重，然后，將權重迭代融合得到最終權重[3]。這種單一的迭代融合在一定程度上有效，然而，由于其很少考慮模型權重之間互相影響的因素，在面對有沖突的證據體時效果不是很好。為了解決這些問題，本文作者采用證據理論建立基于多準則排序證據組合預測模型權重確定算法，通過對證據體建立多準則評價，綜合考慮多種數據源自身信息以及相互之間的互支持信息，確定模型的調整系數，對模型初級權重進行調整，利用多時刻數據確定模型的最終權重，最后根據確定的權重與單一模型預測值確定最終組合預測值。該算法不僅可以用于權重的確定，而且可以作為挑選單一模型的依據。

1 組合預測模型原理

本文組合預測模型原理見圖1。預測模型可以分為4部分，預測基本流程如下。

第1步，單一預測模型的選擇。確定模型類型及其參數。

第2步，單一預測模型初級權重的生成。利用單一預測模型預測結果與相應時刻訓練樣本真值區間之間的距離作為度量單一預測模型預測精度的參數，通過相似性轉換歸一化后作為下一步證據理論要用的基本概率分配BPA，其中BPA矩陣中對于B區間的mass函數值作為單一模型的初級權重。

第3步，計算權重調整系數。利用證據可信度、信任精度和證據自沖突系數3個準則綜合評判證據體的優劣，對各準則進行排序融合得到證據體的綜合排序值作為單一模型的權重調整系數，以減小證據沖突造成的直覺悖論。

第4步，最終的組合預測。利用第3步中改進的證據理論方法求得的調整系數對第2步BPA矩陣中的單一模型初級權重進行調整，確定最終單一模型權重，并進行預測。

圖1 基于多準則排序證據組合預測模型流程圖

2 理論基礎

2.1 組合預測模型

組合預測模型[4]是通過將多個單一預測模型的預測值進行適當加權平均得到最終組合預測結果。

假設種單一預測模型個時刻的預測矩陣為

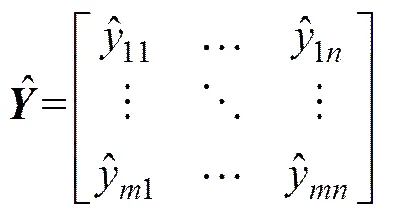
組合預測模型的重點在于計算各個單一模型分配的權重，目前主要有2種方法：第1種是通過擬合實際值分配權重使得加權后預測值與實際值擬合殘差最小，此法只針對所建的目標準則進行評價，不夠全面；另一種是通過對各個單一模型評價綜合信息得到權重。本文基于第2種方法通過不同指標對單一模型進行評價，再分析相互之間影響，以綜合確定最終單一模型權重。

2.2 證據理論

D?S理論[5]用一個具有互斥和可窮舉元素的集合作為它的識別框架(也稱為論域)，通常用表示，記為：。在識別框架上的BPA是1個的函數，稱為mass函數，并且滿足且。對于，上的個mass函數1,2, …,m的Dempster合成規則為

其中：為歸一化常數，其作用是為了避免在合成時將非零概率賦給空集[6]。

證據理論的關鍵在于基本概率分配的準確性和證據合成規則的合理性2個方面，本文基于這2點分別采用區間數基本概率指派生成方法提高BPA的準確性，減小傳統專家法帶來的高沖突問題；同時，利用多指標排序融合方法改進Dempster組合規則，以減小證據組合規則自身存在的問題。

3 新型組合預測模型的建立

3.1 單一模型的選擇

從組合預測模型的組成可以看出組合模型包括2個方面：一個是單一預測模型，另一個是相應的權重系數。這2個元素的選擇都與最終預測結果直接相關，好的單一模型和合適的權重分配非常重要。

單一模型的選擇主要是從模型精度、模型的相關度以及模型的數量3方面綜合考慮。好的模型精度對于結果的預測至關重要，較小的模型之間預測誤差相關性可以減少組合誤差，同時模型的數量過多造成計算量大，而預測結果精度隨模型數量的增多可能提高并不大，數量少可能造成預測效果不好。

基于以上考慮，結合軟件EViews[7]和Matlab[8]進行優化，本文選擇ARMA(2,2)，Holt-Winter-No seasonal(=1，=0)指數平滑法和G(1,1)模型作為單一預測模型。ARMA模型對于模型線性部分有很好的分析效果，指數平滑法主要分析模型的非線性部分產生的影響，灰色模型則是針對整個模型進行整體分析。

3.2 單一模型初級權重的確定

3.2.1 樣本數據的三區間劃分

為了分析單一預測模型與真值樣本的相似性，需確定單一模型的預測值與真值的偏差。本文將真值樣本按照

進行分解，這樣將每一時刻的真值樣本分解成1個以真值為中心點向兩邊擴散的3個區間識別框架，通過計算單一模型預測值落在每個區間的平均距離用于度量單一預測模型的精度，并經過折算生成證據理論的BPA。根據模型權重與基本概率分配的相似性，以最接近樣本真值的B區間的mass函數值(B)作為單一模型的初級權重，通過多種準則對，和3個區間相互之間的關系進行綜合評價，求單一模型的權重調整系數，以×調整模型初級權重，歸一化后作為單一模型最終權重。

3.2.2 區間數基本概率指派生成

應用證據理論的第1步就是確定證據的基本概率分配，這也是證據理論中最重要的一步。據基本概率分配的準確度直接確定下一步證據合成結果。目前確定基本概率分配的方法一般分為兩大類：第1類主要是根據專家經驗主觀確定基本概率分配；第2類主要是根據已知條件自動生成基本概率分配。為了減小專家因個人經驗問題帶來的沖突，本文采用智能化區間數模型生成基本概率分配BPA。區間數只要求給定上、下限2個數據, 建模簡單易行，除了可以減少專家打分法帶來的高沖突問題外，還可以很好地描述信息缺乏不確定度高的應用場合[9]。

應用區間數模型建立單一模型初步權重的步驟如下。

第1步：建立區間數模型。按照式(3)將真值樣本進行區間分割，每一時刻的數據分為3個區間，作為測度單一模型準確度的度量區間。

第2步：計算單一模型預測值與區間數模型之間的距離。根據文獻[10]可利用

第3步：計算單一模型預測值與區間數模型之間的相似性。根據文獻[11]定義區間數相似度為

利用式(6)將得到的距離矩陣轉化為相似度矩陣。

第4步：歸一化處理得到基本概率分配BPA矩陣。對第3步中得到的相似度矩陣按照式(7)進行歸一化處理，得到相應的BPA矩陣。

其中：=，，。

根據BPA與權重的相似性，本文將得到的BPA矩陣作為單一模型時刻點的初級權重，用于后續融合，確定最終權重。

3.3 權重調整系數的確定

證據理論在信息融合領域中具有重要地位，而傳統的Dempster組合規則在遇到沖突證據時常常出現一些違背直覺的悖論，如沖突悖論[12]、信任偏移悖論、證據吸收悖論和焦元基模糊悖論等。對于這些沖突問題，主要有2種改進思路：一種是對證據組合規則進行改進，Florea等提出了一種魯棒的證據組合規則，將交運算和并運算結合起來[13]；另一種是對證據體進行改進，通常先對證據進行預處理，再進行證據組合，代表性的研究成果有Murphy等的研究[13?14]。

單純的改進證據組合規則或者改進證據體都存在一定缺陷，單一的準則往往只能反映證據體的不同側面，不能全面反映證據體的優劣。為了有效地解決證據沖突問題，本文綜合采用證據可信度、證據精度[14]和證據自沖突系數[15]這3種指標對不同證據進行測度，并排序融合作為權重調整系數[13]。

衡量證據之間沖突主要是通過證據距離來衡量，目前主要的證據距離公式有歐氏距離、馬氏距離和余弦距離。這些距離沒有考慮基本概率分配函數包含的信息量即“勢”對信息提取的影響[16]，本文采用Jousselme等[17]提出的可以解決上述問題的證據距離算法，通過將證據體視作向量來表示證據體之間的距離：

利用式(8)的證據距離定義證據體被支持程度為

經綜合考慮，認為證據的受支持程度越高，可信度越大。定義證據體的證據可信度為

證據可信度描述了證據體之間相互支持的程度。為了描述證據自身的不確定性，定義證據精度為

Dempster合成規則中為歸一化常數，而將1?視作證據沖突項，與式(7)的Jousselme距離一樣描述證據沖突，但是并不能全面描述。本文采用文獻[14]中的證據自沖突系數表征證據體的自沖突程度。

其中：m為單點焦元函數，且；系數2的作用是為了使自沖突系數的取值范圍為[0，1]。

本文綜合采用式(11)，(12)和(13)的證據可信度、證據精度和證據自沖突系數來綜合評價證據體，參考文獻[15]并按照式(14)進行排序。

將所得的排序序列按照加權求和作為證據時刻點綜合排序值，以此綜合排序值作為模型的權重調整 系數：

利用式(7)計算的區間基本概率分布與式(15)計算的證據權重調整系數按照下式歸一化計算求得不同單一模型的最終權重：

3.4 最終融合預測

將按照式(16)求得的不同單一模型最終權重代入式(1)進行組合預測并分析。

4 實例分析

選用2011?06—2013?01的金屬鑭月平均價格作樣本數據，根據模型選擇原則，結合EViews和Matlab軟件進行優選，最終選擇ARMA(2,2)，Holt-Winter-No seasonal(=1,=0)指數平滑法和G(1,1)模型作為單一預測模型。

式(3)將真值樣本時刻點數據分解為以3個區間數為元素的識別框架，所以，式(8)中的為×矩陣，經計算可得對稱矩陣為

為評價預測模型的效果，分別選擇平均絕對百分比誤差(MAPE)、均方根誤差(RMSE)和均方百分比誤差(MSPE)這3個指對模型進行評價。單一預測模型預測結果見表1。

表1 金屬鑭價格預測及分析結果

從表1可以看出：G(1,1)模型預測效果最優，ARMA(2,2)效果相對最差，而Holt-Winter-No seasonal (=1,=0)指數平滑法預測效果中等。

針對樣本數據，本文研究調整系數、區間劃分以及權重是否變化對組合預測結果的影響。

當沒有調整系數時，直接以(B)作為單一預測模型最終權重，結果指標見表2。從表2可以看出：可變權模型預測效果要優于不變權模型的可變權模型預測效果。

表2 無調整系數組合預測結果

為了分析式(15)調整系數的合理性，根據證據體證據信任度和證據精度與融合結果正相關，而證據自沖突系數與融合結果反相關，另外定義第2種調整系數為

區間的劃分也會對最終結果產生影響，不同的區間會產生不同的(B)，本文分2種情況探討等區間劃分和不等區間劃分。

對不同區間劃分和調整系數組合方式進行組合預測，不變權組合預測模型權重見表3，預測結果評價指標見表4~5。

表3 不變權組合模型權重

表4 區間劃分(a)組合預測分析結果

表5 區間劃分(b)組合預測分析結果

從表4~5可以看出：可變權組合模型的預測結果要優于不變權組合模型預測結果。分別對比表4和表5發現：采用可變權組合模型時，調整系數比調整系數有更好的效果；當采用不變權組合模型時，利用調整系數比調整系數有更好的效果。不等區間劃分的比等區間劃分效果較好。這是因為中間不等區間劃分時，區間的劃分更集中于樣本真值，具有更好的單一模型初級權重(B)。

雖然可變權組合模型的預測效果要優于不變權模型的預測效果，但在實際使用過程中，由于可變權重是隨時間變化的，對于后期的預測還需要提前預測權重，這就增加了模型的不確定性，所以，在實際中采用不變權組合模型更加實用。對比表2~5中不變權可以發現：經過調整系數處理后的預測結果要明顯優于調整系數和無調整系數處理過的結果，這也證明了本文權重調整方法的優越性。

綜上所述可知：選用不變權、以為單一模型權重調整系數且識別框架中間區間越趨近于真值樣本的模型，最后的組合預測結果效果更實用、更精確。

5 結論

1) 本文通過優選利用ARMA(2,2)，Holt-Winter- No seasonal(=1，=0)指數平滑法和G(1,1)模型對金屬鑭月平均價格進行訓練預測，然后通過區間數模型處理預測數據生成證據理論所需的BPA，以基于樣本時刻點數據的BPA值作為單一模型的初級權重，再利用證據可信度、證據精度和證據自沖突系數這3個準則分析BPA矩陣各證據體之間的互支持信息對單一模型進行綜合評價，對最終的指標排序值進行處理生成單一模型的權重調整系數，最終經過歸一化處理得出各組合預測模型最終權重，并進行預測。

2) 通過考慮單一模型之間的互支持信息對模型初級權重進行調整，并且選擇合適的調整系數，區間劃分方式都將對組合預測結果產生明顯影響。本文提出的基于多準則排序證據組合預測模型權重確定算法可以顯著提高組合預測模型預測精度。

[1] Bates J M, Granger C W J. The combination of forecasts[J]. Operational Research Society, 1969, 20(4): 451?468.

[2] 邱望仁, 劉曉東. 基于證據理論的模糊時間序列預測模型[J]. 控制與決策, 2012, 27(1): 99?103. QIU Wangren, LIU Xiaodong. Fuzzy time series model for forecasting based on Dempster-Shafer theory[J]. Control and Decision, 2012, 27(1): 99?103.

[3] 吳京秋, 孫奇, 楊偉, 等. 基于D?S證據理論的短期負荷預測模型融合[J]. 電力自動化設備, 2009, 29(4): 66?70. WU Jingqiu, SUN Qi, YANG Wei, et al. The short-term load forecasting based on D?S evidential theory[J]. Electric Power Automation Equipment, 2009, 29(4): 66?70.

[4] 戴華娟. 組合預測模型及其應用研究[D]. 長沙: 中南大學數學與統計學院, 2007: 6?24.. DAI Huajuan. Research on combination forecast and its application[D]. Changsha: Central South University. School of Mathematics and Statistics, 2007: 6?24.

[5] 韓崇昭, 朱洪艷, 段戰勝, 等. 多源信息融合[M]. 2版. 北京: 清華大學出版社, 2010: 82?92. HAN Chongzhao, ZHU Hongyan, DUAN Zhansheng, et al. Multi-source information fusion[M]. 2nd ed. Beijing: Tsinghua University Press, 2010: 82?92.

[6] 葉清, 吳曉平, 宋業新. 基于權重系數與沖突概率重新分配的證據合成方法[J]. 系統工程與電子技術, 2006, 28(7): 1014?1016, 1081. YE Qing, WU Xiaoping, SONG Yexin. Evidence combination method based on the weight coefficients and the confliction probability distribution[J]. Systems Engineering and Electronics, 2006, 28(7): 1014?1016, 1081.

[7] 易丹輝. 數據分析與EViews應用[M]. 北京: 中國人民大學出版社, 2009: 98?148. YI Danhui. Data analysis and application of reviews[M]. Beijing: Renmin University of China Press, 2009: 98?148.

[8] 張志涌. 精通MATLAB(6.5版)[M]. 北京: 北京航空航天大學出版社, 2006: 27?85. ZHANG Zhiyong. Proficient in MATLAB(Version 6.5)[M]. Beijing: Beihang University Press, 2006: 27?85.

[9] Wan S P. Interval number method for object threat assessment[J]. Computer Engineering and Applications (China), 2009, 45(6): 32?34.

[10] Tran L, Duckstein L. Comparison of fuzzy numbers using a fuzzy distance measure[J]. Fuzzy Sets and Systems, 2002, 130(3): 331?341.

[11] 康兵義, 李婭, 鄧勇, 等. 基于區間數的基本概率指派生成方法及應用[J]. 電子學報, 2012, 40(6): 1092?1096. KANG Bingyi, LI Ya, DENG Yong, et al. Determination of basic probability assignment based on interval numbers and its application[J]. Acta Electronica Sinica, 2012, 40(6): 1092?1096.

[12] Zadeh L A. Review of a mathematical theory of evidence[J]. AI Magazine, 1984, 5(3): 81?83.

[13] Powell G, Roberts M. GRP1. A recursive fusion operator for the transferable belief model[C]// Proceedings of the 14th International Conference on Information Fusion. Chicago, USA: IEEE, 2011: 168?175.

[14] Smarandache F, Martin A, Osswald C. Contradiction measures and specialty degrees of basic belief assignments[C]// Proceedings of the 14th International Conference on Information Fusion. Chicago. USA: IEEE, 2011: 475?482.

[15] 楊藝, 韓德強, 韓崇昭. 基于多準則排序融合的證據組合方法[J]. 自動化學報, 2012, 38(5): 823?831. YANG Yi, HAN Deqiang, HAN Chongzhao. Evidence combination based on multi-criteria rank-level fusion[J]. Acta Electronica Sinica, 2012, 38(5): 823?831.

[16] 于東平, 段萬春, 孫永河. 基于最優權重的多源證據加權平均合成算法研究[J]. 統計與決策, 2011(10): 16?19. YU Dongping, DUAN Wanchun, SUN Yonghe. Research on weighted average algorithm of multi-source evidence based on optimal weight[J]. Control and Decision, 2011(10): 16?19.

[17] Jousselme A L, Grenier D, Bossé é. A new distance between two bodies of evidence[J]. Information Fusion, 2001, 2(2): 91?101.

Research and application of multi-criteria combination forecast model

HUANG Rendong1, ZHANG Haibin1, YANG Zhihui2, ZHOU Yang1, ZHANG Pan1

(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;2. School of Metallurgy and Environment, Central South University, Changsha 410083, China)

Considering that most of traditional combination forecast models are established by criterion of single equation regardless of information between individual model which implicits lots of uncertainty, a weight determination algorithm of combination forecast model was presented based on multi-criteria information. Firstly, interval numbers model was built to getthe sample BPA matrix as the primary weight of the single models by a series of distance calculations between the true data and the predictive value. Then, three criteria, i.e. evidence credibility, evidence precision and evidence contradiction, were set up to evaluate the precision of individual model and information between them. By sequencing the above three criteria, a composite sort value called weight adjustment coefficient was generated to adjust the primary weight of the single models. Finally, the final weight was determined by normalizing the multi-time weight data used for combination forecast. The results show that the precision of the method is high, one fixed weight combination forecast model adjusted by weight adjustment coefficientis the best.

combination forecast; evidence theory; weight adjustment coefficient; credibility; evidence precision; evidence contradiction

10.11817/j.issn.1672-7207.2015.05.028

TD983

A

1672?7207(2015)05?1778?08

2014?06?12；

2014?08?22

國土資源部公益性行業科研專項課題(201211067-3) (Project(201211067-3) supported by Public Service Industry Special Scientific Research of Ministry of Land and Resources)

黃仁東，教授，從事礦產安全開采理論與技術研究；E-mail: hldlb@163.com

(編輯 陳燦華)