基于分裂Bregman迭代的混合正則化重力場反演

曹書錦，朱自強，魯光銀

?

基于分裂Bregman迭代的混合正則化重力場反演

曹書錦，朱自強，魯光銀

(中南大學地球科學與信息物理學院，湖南長沙，410083)

針對重力場反演中深度分辨率過低的問題，提出基于混合稀疏正則化聯(lián)合反演。引入L1多尺度小波和全變差技術，使在剔除干擾異常及規(guī)避反演過度聚焦的同時，盡可能地保留深度方向上的分辨率；針對在混合正則化反演中預條件矩陣左乘(求逆)計算量過大的問題，構建新的深度權項實現(xiàn)基于最小分裂Bregman迭代算法快速三維密度反演成像。研究結果表明：本文反演方法可行、有效，具有較強的適應性。

混合正則化；分裂Bregman迭代算法；深度加權矩陣；多尺度小波；全變差正則化

由于反演著重點或目的不同，所需要建立的反演模型也不同，同時也決定了反演的總體設計、反演過程、反演特征及反演效果等不同。本質上，每種正則化方法都有一定的側重性，而在面對較復雜的地質構造時，這種優(yōu)勢即轉變成過度正則化效應。同時，由于重力異常的幅值隨著地下物性網(wǎng)格質心深度的增加而迅速衰減，導致反演深度分辨率過低[1]，如何得到更清晰的地質界面仍是當前地球物理反演研究的一個重點問題。在過去的十幾年中，眾多研究者在邊界識別/邊界保存的位場反演技術如全變差正則化[2]、聚焦反演[3]和尖銳邊界/陡邊界反演[4]等方面進行了大量的研究。Tikhonov正則化雖然具有成像速度快、求解穩(wěn)定、定位準確等優(yōu)點，但由于該算法導出的是最小二乘問題近似解，導致目標區(qū)域與背景區(qū)域間的邊界模糊，成像效果不好，分辨能力較低，多個物體之間存在偽跡。全變差正則化算法能在對問題進行反演過程中得到跳躍性較大的參數(shù)部分，有效地避免了物性邊界的過度光滑，使得目標區(qū)域與背景區(qū)域間的邊界分明，具有很好的保邊緣性[5]。僅在先驗地質信息充足的情況下，尖邊界反演方法才能取得很好的反演效果，但其對初始模型的設置和先驗地質信息的準確性要求較高，難于滿足起伏地形條件下的反演需求，且存在反演深部構造不夠準確以及加入約束條件較困難等不足[6]。聚焦反演具有成像快速、對單一異常聚焦效果明顯等優(yōu)點，但由于存在過度正則化效應，在地質構造復雜且各構造權重不均一的情況下，其易導致構造形態(tài)發(fā)生畸變及對目標區(qū)域的定位不準確[7]。為此，本文作者引入一類多尺度小波稀疏算子，以期在邊界保持的同時借助其具有的一定光滑效應，在此基礎上引入具有邊界保持特性的全變差算子，將兩者在分裂Bregman迭代算法的框架下有機地實現(xiàn)混合正則化反演[8]。針對在分裂Bregman迭代算法框架下的預條件算子構建難度大(即當預條件矩陣為左除矩陣時，其為稀疏矩陣，由于每次反演迭代都需要計算其臨時中間逆矩陣，但其逆矩陣為非稀疏矩陣，因而導致不能有效地存儲預條件矩陣的逆矩陣)，引入一類與場源衰減特性無關的預條件矩陣，以實現(xiàn)快速反演。使用2組不同模型(同一深度與不同深度)和實際觀測數(shù)據(jù)，對比研究多類位場反演方法在不同深度異常的適應性，并通過數(shù)值模型和實際觀測數(shù)據(jù)的反演驗證本文算法的正確性，即對不同深度異常的適應性。

1 混合正則化反演

將反演的地下空間劃分為大小相等、緊密排列的立方體格網(wǎng)單元，且任一立方體內部的密度均勻[9]。重力正演可以表示如下：

其中：表示觀測重力，可具體為g；為示模型空間密度分布的重力正演核函數(shù)；物性參數(shù)向量。重力場物性反演待求的參數(shù)就是各網(wǎng)格單元內的密度。傳統(tǒng)位場反演等價于求解線性方程(1)的反問題，利用正則化理論構建三維反問題[10]：

其中：()通常為L1或L2罰項，為模型泛函；為數(shù)據(jù)泛函，為正則化參數(shù)。

單一正則化方法都有一定的側重性，也意味著對相應的問題具有非常重要的單一優(yōu)勢，而在面對較復雜的地質構造時，這種優(yōu)勢則轉變成過度正則化效應。為確保反演的穩(wěn)定性和健全性，又不損失重構結果的分辨率，引入L1多尺度小波[11?12]與全變差正則化算子[13]以構建重力場聯(lián)合稀疏約束反演目標函數(shù)，以期在保留位場多尺度特征的同時，增強邊界區(qū)分的能力，從而在更好地得到清晰構造邊界的同時快速而穩(wěn)定地求解。聯(lián)合稀疏約束反演的可通過修改式(2)實現(xiàn)[8]：

使用L1范數(shù)，則有[15]

其導數(shù)為

其中，導數(shù)定義為：

；

；

；

。

其中：h，h和h分別為物性網(wǎng)格在，和方向的邊長。函數(shù)(,)的定義為

其中：sign為符號函數(shù)，

當與的方向相反時，(,)則等于0。對于在物性不連續(xù)接觸界面(如斷層接觸面、地層分界面等)，

通常采用重加權迭代最小二乘法序貫求解式(3)[16]，但采用傳統(tǒng)的序貫方法解混合正則化優(yōu)化問題的效率較低。在解混合正則化問題上，Wright[17]提出了固定點迭代算法，但其僅為線性收斂，存在收斂速度慢的問題；Goldstein等[10]提出了分裂迭代正則化算法，以降低模型的計算復雜性；Jia等[18]在其基礎上，對其收斂性進行了進一步分析。為此，對式(3)引入收斂更快的最小分裂Bregman迭代算法框架以實現(xiàn)重力場聯(lián)合稀疏約束反演。利用1和2分別替換式(3)中的和等2項，得一約束優(yōu)化問題[10]：

將式(5)轉化為無約束優(yōu)化問題：

對式中求導，并令求導式等于0，則迭代形式為

其中：

2 深度加權

用式(6)進行物性反演，其目標是取得地下物性的分布。由于重力沒有或較少含有深度方向的信息，且在深度方向的分辨率較低，其確定異常邊緣上的能力較強，主要源于重力異常的幅值與場源到觀測點的距離的冪次方成反比，而使重力異常的幅值隨著物性網(wǎng)格質心深度的增加而迅速衰減產生的趨膚效應，導致重構結果的密度分布趨向地表附近，而不是按照地質體的真實深度分布，因此，可以通過引入深度加權函數(shù)近似地補償核系數(shù)矩陣隨著深度的衰減。僅考慮深度方向的上距離而忽略觀測點與密度體水平方向上的差異，可以使用近似反映核函數(shù)隨著深度的衰減。Li等[19]在三維磁化率反演中，引入深度加權函數(shù)：

式中：為物性網(wǎng)格質心埋深；0為常數(shù)，取決于物性網(wǎng)格的邊長以及觀察面高度；為衰減因子，取決于地球物理位場的場源特性。通過調整0和，以近似表達反演核函數(shù)的趨膚效應。

混合正則化反演其主要受式(6)的求解速度控制，尤其是進行海量面數(shù)據(jù)的三維反演時，這種瓶頸效應更加明顯。為了加快反演速度，應該使反演收斂速度更快、迭代次數(shù)盡可能小并減少反演核矩陣參與運算的次數(shù)。式(6)的收斂受系數(shù)矩陣的條件數(shù)控制，對于三維密度成像反演而言，其系數(shù)矩陣的條件數(shù)很大，一般可以通過左乘1個預條件矩陣優(yōu)化目標函數(shù)。Pilkington[20]引入深度加權矩陣式(7)到三維磁化率反演目標函數(shù)中，得出簡單可靠的預條件矩陣(其中=3.0，為單位矩陣)，并得到了比較理想的結果。但在重力反演中，一般為1.5~2.0[21]；在重力梯度反演中，一般為2.0~3.0；在磁化率反演中，=3.0[20]。這致使在重力場多分量聯(lián)合反演中難以確定。對于混合正則化密度反演，其預條件矩陣為

對于小模型密度反演成像問題，直接對式(6)左乘預條件矩陣2其計算效率將很快。但對大尺度模型的三維物性反演，引入預條件共軛梯度法可快速近似地計算式(6)[22]；當混合正則化反演中兩正則項分別為多尺度小波算子和全變差算子時，的預條件算子可近似地為其自身的對角矩陣：

2與3均為稀疏帶狀矩陣，因而，其左乘(求逆)的計算和存儲成本遠遠比1的高，且對于相對較大模型的三維密度反演成像時，3的逆矩陣將極難計算或存儲。但由于1應用于多階重力場聯(lián)合反演并不準確，通過以上3類預條件算子1，2與3相比，選擇一個更簡單的基于反演核矩陣的先驗深度權[23]：

因此，在不考慮物性網(wǎng)格在水平方向上的差異及網(wǎng)格邊界效應的影響時，將隨著物性網(wǎng)格深度的增大而減小。若應用于(2)式，則將優(yōu)先約束在淺層網(wǎng)格上，從而使得在作用深部的物性網(wǎng)格權重更大[24]，此時，便可以作為求解式(6)的預條件矩陣。

引入深度加權項式(8)，對式(2)改寫為

類似于式(3)，引入2個稀疏正則化項，并將數(shù)據(jù)泛函的正則化參數(shù)縮并到兩混合正則化參數(shù)內：

深度加權的分裂Bregman迭代無約束優(yōu)化算法的具體實施步驟如下。

1) 選定誤差限t、正則化參數(shù)和。

4) 鑒于在地球物理重磁場反演時，通常使用非線性共軛梯度法或預條件共軛梯度法易于獲得光滑邊界，而難于獲得尖銳邊界。因此，利用重加權正則化共軛梯度法求解式(10)以實現(xiàn)重力場聯(lián)合稀疏約束反演。多正則化參數(shù)的重加權正則化共軛梯度法算法流程見文獻[3, 25]。

5) 利用soft?shrinkage公式[26]對式(5)中約束項更新：

7) 重復步驟3)~6)，直至滿足反演終止條件為止。

3 模型實驗

3.1 實驗模擬Ⅰ

如圖1(a)所示，構建1個含有2個同深度異常體的模型對上述方法原理進行驗證。2個異常體的長×寬×高均為200 m×200 m×200 m，異常體頂板埋深均為200 m，底板埋深為為400 m，剩余密度均為1.0 g/cm3。將場源空間劃分為20×20×10=4 000個單元格，每個單元格沿，和軸方向的長度均為50 m；觀測網(wǎng)測點高度為25 m，測點間距為50 m，共有20×20=400個采集數(shù)據(jù)。

(a) 正演模型；(b) 光滑反演結果；(c) Marquardt 反演結果[27]；(d) Occam反演結果[28]；(e) 聚焦反演結果[29]；(f) 混合正則化反演結果

反演數(shù)據(jù)為添加3%的高斯白噪聲的正演模擬結果。在光滑反演、Marquardt反演及Occam反演中，=4，a=1，a=1，a=1，a=0.000 5，=1.8，如圖1(a)~(d)所示[27?29]；在圖1(e)中，聚焦算子為，=1.2×10?6；圖1(f)中，混合正則化反演的參數(shù)為=0.01，=0.1，=1。在圖1(b)，(c)和(d)中三者效果相當，三者在深度上的分辨率均較低，尤以光滑反演(圖1(b))在深度上的分辨率最低，異常底板分界面非常模糊，難以辨識；而聚焦反演取得了較清晰的邊界，由于聚焦作用的影響，存在過度聚焦的現(xiàn)象(圖1(e))，即反演得出異常的規(guī)模遠比實際的要小，而異常幅值要比實際正演模型的大得多。相比于聚焦反演(如圖1(f)所示)，本文混合正則化反演方法的聚焦作用更明顯，但其反演輪廓與正演模型的相當。

3.2 實驗模擬Ⅱ

構建1個含2個不同深度異常體的模型對上述方法原理進行驗證，如圖2(a)所示。2個異常體長×寬×高均為200 m×200 m×200 m；右側異常體頂板埋深為200 m，底板為400 m，左側異常體頂板埋深均為300 m，底板為500 m；剩余密度均為1.0 g/cm3。將場源空間劃分為20×20×16=6 400個單元格，每個單元格沿，和軸方向的長度均為50 m；觀測網(wǎng)測點高度為25 m，觀測點間距為50 m，總共有20×20=400個采集數(shù)據(jù)。

(a)正演模型；(b) 光滑反演結果；(c) Marquardt 反演結果[27]；(d) Occam反演結果[28]；(e) 聚焦反演結果[29]；(f) 混合正則化反演結果

反演數(shù)據(jù)為添加3%的高斯白噪聲正演模擬結果，在光滑反演、Marquardt反演及Occam反演中，=4，a=1，a=1，a=1，a=0.000 5，=1.8，如圖2(a)~(d)所示；在混合正則化反演中，=0.01，=0.1，=1，如圖2(f)所示。在圖2(b)，(c)和(d)中三者效果相當，異常底板分界面非常模糊，難以辨識；而聚焦反演取得了較為清晰的邊界(圖2(e))，將兩者區(qū)分開來，但其反演推斷異常空間位置與正演模型的存在較大偏差，尤其在深度方向存在差異較大。這主要受到聚焦算子的適應性和聚焦閥值的難以選取的影響，此處聚焦算子為，=0.001，其中與前次模型(即圖1(e))相差很大，其原因為：在限制反演密度模型上限的同時(異常幅值上限為1.2 g/cm3)，進一步提高了深度方向上的聚焦效應。相比于聚焦反演，本文反演方法的聚焦作用更明顯，其聚焦作用介于Occam反演、Smoothness反演和Marquardt反演這三者與聚焦反演之間，其反演結果輪廓與正演模型的相當，且深度與實際正演模型的相當(圖2(f))。與其他反演方法相比，混合正則化反演具有更強的適應性。

4 實例

加拿大卑詩省在2007年設施1個旨在為吸引礦業(yè)投資者向地質構造復雜、勘探程度較低、潛在成礦潛力巨大的British Columbia地區(qū)投資的地球物理及地球化學綜合勘探項目[30]。本文實例采用該項目組中的1個名為Quest—South的測區(qū)，見圖3。為便于處理，選取其中1個矩形測區(qū)(見圖4)。在測區(qū)內地勢從丘陵到連綿陡峭的山脈，海拔高程為?150~370 m。

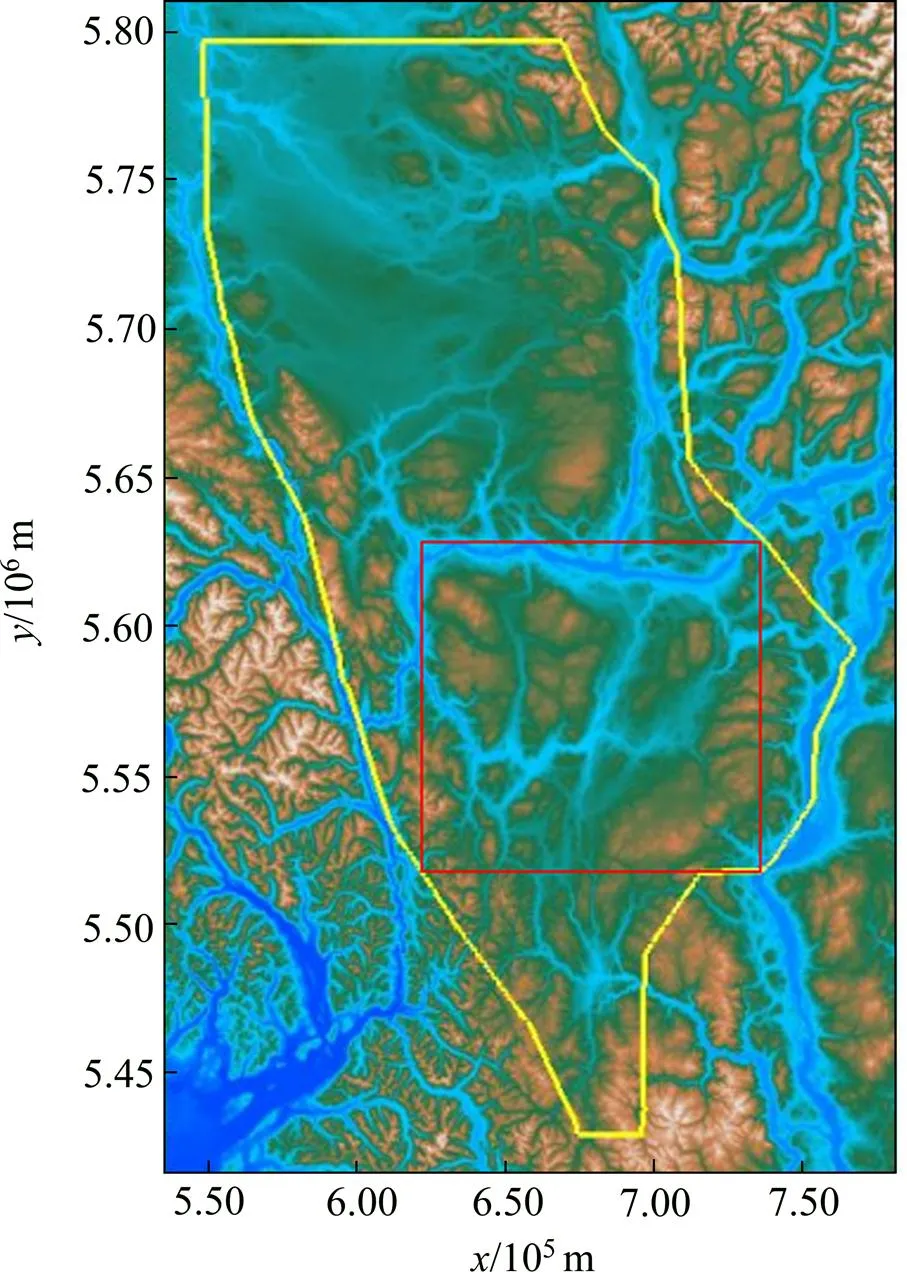
圖3 Quest South測區(qū)示意圖[30]

圖4 重力異常

為對重力異常進行分離，用向上延拓到3 km平面的重力場作為區(qū)域場，將區(qū)域異常從重力異常中減去從而得到剩余異常場，見圖5。

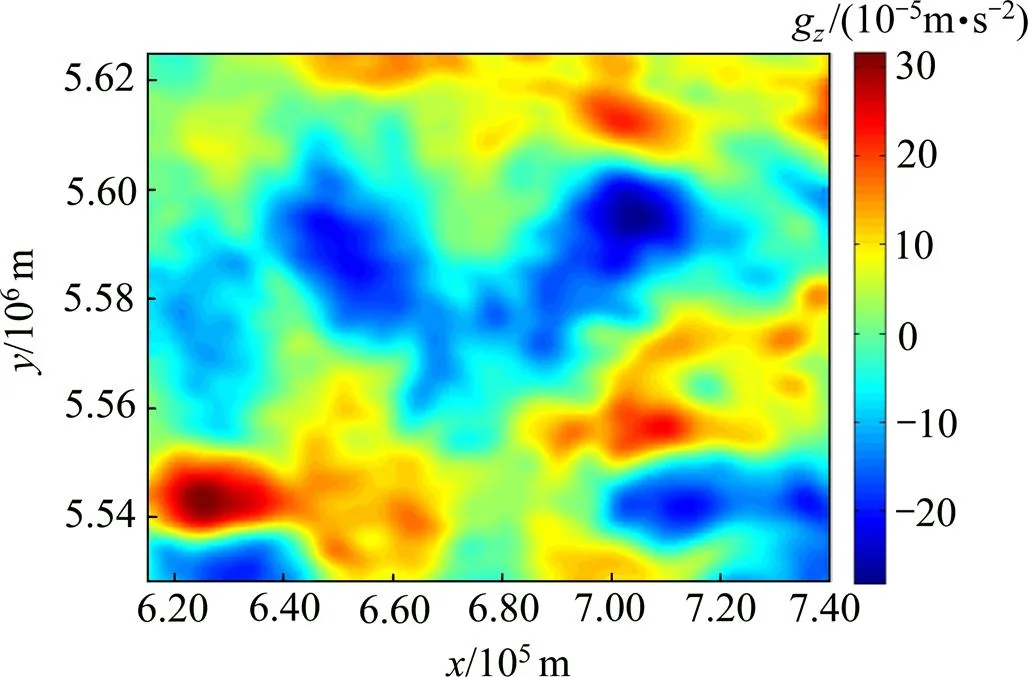
圖5 局部重力異常

從圖5可以發(fā)現(xiàn)反演算法在淺部的正異常取得了較清晰的結果。反演密度切片見圖6。圖6中的(1)，(3)和(4)號異常均具有較清晰的邊界；而圖6中的(2)和(5)號異常所示在深部反演的分辨率有所下降，這主要受到區(qū)域場和剩余異常場劃分的影響。

圖6 混合正則化重力場反演結果組合切片圖

5 結論

1) 分析了混合正則化框架下預條件算子的實現(xiàn)及計算性能，給出了適合多階重力場分量的深度權公式，并在此基礎上給出了混合正則化反演算法。

2) 充分對比了多類單一正則化反演方法，引入基于L1多尺度小波正則項和全變差正則的混合正則化，在剔除無效異常的同時，盡可能地保留深度方向上的分辨率及在邊界上的識別能力。

3) 與其他反演方法相比，混合正則化反演對不同深度異常源具有更強的適應性，并有效地避免了聚焦反演存在的過度聚焦現(xiàn)象。

[1] 姚長利, 郝天珧, 管志寧, 等. 重磁遺傳算法三維反演中高速計算及有效存儲方法技術[J]. 地球物理學報, 2003, 46(2): 2252?2258. YAO Changli, HAO Tianyan, GUAN Zhining, et al. High speed computation and efficient storage in 3D gravity and magnetic inversion based on genetic algorithms[J]. Chinese Journal of Geophysics, 2003, 46(2): 2252?2258.

[2] 李星秀, 韋志輝. 形態(tài)成分正則化約束的圖像恢復方法[J]. 計算機工程與應用, 2010,46(17): 27?29. LI Xingxiu, WEI Zhihui. Image restoration via regularization constraints of morphological components[J]. Computer Engineering and Applications, 2010, 46(17): 27?29.

[3] Zhdanov S. Geophysical inverse theory and regularization problems[M]. Boston: Elsevier Science Ltd, 2002: 155?165.

[4] 張羅磊, 于鵬, 王家林, 等. 光滑模型與尖銳邊界結合的MT二維反演方法[J]. 地球物理學報, 2009, 52(6): 1625?1632. ZHANG Luolei, YU Peng, WANG Jialin, et al. Smoothest model and sharp boundary based two-dimensional magnetotelluric inversion[J]. Chinese Journal of Geophysics, 2009, 52(6): 1625?1632.

[5] 岳建惠. 電阻率成像反問題的混合正則化方法研究[D]. 大連: 大連海事大學應用數(shù)學系, 2012: 4?5. YUE Jianhui. Research of mixture regularization methods for EIT inverse problem[D]. Dalian: Dalian Maritime University. Department of Applied Mathematics, 2012: 4?5.

[6] 譚捍東, 余欽范, John B, 等. 大地電磁法三維快速松弛反演[J]. 地球物理學報, 2003, 46(6): 1218?1226. TAN Handong, YU Qinfan, John B, et al. Three-dimensional rapid relaxation inversion for the magnetotelluric method[J]. Chinese Journal of Geophysics, 2003, 46(6): 1218?1226.

[7] 黃嵩. 電阻抗靜態(tài)成像中正則化算法研究[D]. 重慶: 重慶大學電氣工程學院, 2005: 27?50. HUANG Song. Regularization algorithm research of static electrical impedance tomography[D]. Chongqing: Chongqing University. College of Electrical Engineering, 2005: 27?50.

[8] Gholami A, Siahkoohi H. Regularization of linear and non-linear geophysical ill-posed problems with joint sparsity constraints[J]. Geophysical Journal International, 2010,180(2): 871?882.

[9] LI Xiong, Chouteau M. Three-dimensional gravity modeling in all space[J]. Surveys in Geophysics, 1998, 19(4): 339?368.

[10] Goldstein T, Osher S. The split Bregman method for L1- regularized problems[J]. SIAM Journal on Imaging Sciences, 2009,2(2): 323?343.

[11] Davis K, Li Y. Efficient 3D inversion of magnetic data via octree mesh discretization, space-filling curves, and wavelets[J]. SEG Technical Program Expanded Abstracts, 2010, 29(1): 1172?1177.

[12] Davis K, LI Yaoguo. Fast solution of geophysical inversion using adaptive mesh, space-filling curves and wavelet compression[J]. Geophysical Journal International, 2011, 185: 157?166.

[13] Routh S, Qu L, Sen K, et al. Inversion for non-smooth models with physical bounds[J]. SEG Technical Program Expanded Abstracts, 2007, 26(1): 1795?1799.

[14] Bertete-Aguirre H, Cherkaev E, Oristaglio M. Non-smooth gravity problem with total variation penalization functional[J]. Geophysical Journal International, 2002,149(2): 499?507.

[15] Loris I, Verhoeven C. Iterative algorithms for total variation-like reconstructions in seismic tomography[J]. International Journal on Geomathematics, 2012, 3(2): 179?208.

[16] Abbasbandy S. Improving Newton-Raphson method for nonlinear equations by modified a domian decomposition method[J]. Applied Mathematics and Computation, 2003, 145(2): 887?893.

[17] Wright J. Primal-dual interior-point methods[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1997: 127?156.

[18] Jia R Q, Zhao H, Zhao W. Convergence analysis of the Bregman method for the variational model of image denoising[J]. Applied and Computational Harmonic Analysis, 2009, 27(3): 367?379.

[19] LI Yaoguo, Oldenburg W. 3-D inversion of magnetic data[J]. Geophysics, 1996, 61(2): 394?408.

[20] Pilkington M. 3-D magnetic imaging using conjugate gradients[J]. Geophysics, 1997,62(4): 1132?1142.

[21] LI Yaoguo, Oldenburg W. 3-D inversion of gravity data[J]. Geophysics, 1998, 63(1): 109?119.

[22] Koh K, Kim S J, Boyd P. An interior-point method for large-scale L1-regularized logistic regression[J]. Journal of Machine Learning Research, 2007, 8(8): 1519?1555.

[23] Portniaguine O, Zhdanov S. 3-D magnetic inversion with data compression and image focusing[J]. Geophysics, 2002, 67(5): 1532?1541.

[24] Pilkington M. 3D magnetic data-space inversion with sparseness constraints[J]. Geophysics, 2008,74(1): L7?L15.

[25] ZHANG Luolei, YU Peng, WANG Jialin, et al. Smoothest model and sharp boundary based two-dimensional magnetotelluric inversion[J]. Chinese Journal of Geophysics, 2009, 52(6): 1360?1368.

[26] WANG Yilun, YIN Wotao, ZHANG Yin. A fast algorithm for image deblurring with total variation regularization[R]. Texas: Technical Report TR07-10 of Rice University Computational and Applied Mathematics, 2007: 1?19.

[27] Thanassoulas C, Tselentis G A, Dimitriadis K. Gravity inversion of a fault by marquardt’s method[J]. Computers & Geosciences, 1987,13(4): 399?404.

[28] Constable C, Parker L, Constable G. Occam’s inversion: A practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 1987, 52(3): 289?300.

[29] Zhdanov M, Ellis R, Mukherjee S. Three-dimensional regularized focusing inversion of gravity gradient tensor component data[J]. Geophysics, 2004, 69(4): 925?937.

[30] Reichheld S. Documentation and assessment of exploration activities generated by geoscience BC data publications[R]. British Columbia, CANADA: Geoscience BC, 2013: 125?130.

Gravity inversion based on hyper-parameter regularization inversion via iteration splitting bregman algorithm

CAO Shujin, ZHU Ziqiang, LU Guangyin

(School of Geosciences and Info-Physics, Central South University, Changsha 410083, China)

Considering the depth resolution of gravity inversion is too low, a hyper-parameter regularization algorithm based on multi-scale L1 wavelet operator and total variation operator was proposed. Regarding the difficulty to calculate the inverse matrix of preconditioning matrix, a new preconditioner was introduced to carry out the hyper-parameter regularization inversion, which was solved by the minimum splitting Bregman iterative algorithm. The results show that the proposed method is vilid and effective, and has strong adaptability.

hyper-parameter regularization; splitting Bregman iterative algorithm; depth weighting matrix; multi-scale wavelet; total variation operator

10.11817/j.issn.1672-7207.2015.05.018

P631

A

1672?7207(2015)05?1699?08

2014?05?28；

2014?07?21

國家自然科學基金資助項目(41174061, 41374120) (Projects(41174061, 41374120) supported by the National Natural Science Foundation of China)

曹書錦，博士，從事地球物理勘探數(shù)據(jù)處理與反演等研究；E-mail: shujin.cao@163.com

(編輯 陳燦華)