考慮下部結(jié)構(gòu)支承剛度的大跨度屋蓋風(fēng)致響應(yīng)分析

陳智勇，彭振斌，陳偉

?

考慮下部結(jié)構(gòu)支承剛度的大跨度屋蓋風(fēng)致響應(yīng)分析

陳智勇1，彭振斌1，陳偉2

(1. 中南大學(xué)地球科學(xué)與信息物理學(xué)院，湖南長(zhǎng)沙，410083；2. 廣州工程總承包集團(tuán)有限公司，廣東廣州，510030)

在對(duì)廣州國(guó)際體育演藝中心實(shí)施剛性測(cè)壓模型風(fēng)洞實(shí)驗(yàn)的基礎(chǔ)上，對(duì)分別采用整體模型與簡(jiǎn)化整體模型對(duì)其上部大跨度空間屋蓋鋼結(jié)構(gòu)的風(fēng)致動(dòng)力響應(yīng)進(jìn)行對(duì)比分析與研究。同時(shí)，在分析結(jié)構(gòu)風(fēng)致振動(dòng)響應(yīng)計(jì)算方法時(shí)，分別采用傳統(tǒng)的多階自由振動(dòng)模態(tài)和基于荷載的Ritz向量模態(tài)進(jìn)行對(duì)比分析，其中基于荷載的Ritz向量求解所需的初始荷載模式通過(guò)本征正交分解(POD)技術(shù)獲得。研究結(jié)果表明：簡(jiǎn)化整體模型風(fēng)致響應(yīng)的計(jì)算結(jié)果比整體模型的風(fēng)致動(dòng)力響應(yīng)稍大，其主要原因是在采用相同數(shù)目的參振模態(tài)時(shí)，簡(jiǎn)化整體模型所包含的對(duì)屋蓋風(fēng)致響應(yīng)有直接貢獻(xiàn)的模態(tài)比整體模型的模態(tài)多；所提出的基于屋蓋表面風(fēng)荷載的Ritz向量法求解僅使用少數(shù)參振模態(tài)，即可獲得傳統(tǒng)模態(tài)疊加法同樣精度的風(fēng)致振動(dòng)響應(yīng)，說(shuō)明該方法是有效的。

大跨屋蓋結(jié)構(gòu)；風(fēng)致響應(yīng)；Ritz向量；POD分解

一般的大跨度體育場(chǎng)館主要由上部的大跨度空間屋面和其下部支承的混凝土框架結(jié)構(gòu)看臺(tái)和輔助用房組成，上、下部結(jié)構(gòu)之間通過(guò)屋蓋底部支座相連接。由于下部混凝土結(jié)構(gòu)組成一般復(fù)雜，桿件眾多，因此，在進(jìn)行上部屋蓋風(fēng)致響應(yīng)分析時(shí)，若計(jì)算模型將上部屋蓋和下部支承混凝土結(jié)構(gòu)全部計(jì)入，則有限元計(jì)算和屋蓋風(fēng)致振動(dòng)分析的工作量很大。考慮到體育場(chǎng)館中結(jié)構(gòu)自身的組成特點(diǎn)，其上部大跨度空間結(jié)構(gòu)與下部支承混凝土結(jié)構(gòu)相比剛度要小得多，因此，僅考慮以上部大跨度空間結(jié)構(gòu)本身為基礎(chǔ)的簡(jiǎn)化整體模型，并考慮上部屋蓋和下部混凝土支承結(jié)構(gòu)的相互作用，這樣既可以考慮上、下部結(jié)構(gòu)兩者之間的共同作用，又可以大大減少大跨屋蓋風(fēng)振響應(yīng)計(jì)算的工作量[1?2]。另外，大跨度屋蓋結(jié)構(gòu)由于采用輕質(zhì)高強(qiáng)材料，在屋蓋自重降低的同時(shí)，結(jié)構(gòu)剛度也日趨變?nèi)幔沟闷鋵?duì)風(fēng)的敏感性日益增強(qiáng)，風(fēng)荷載已成為該類結(jié)構(gòu)設(shè)計(jì)中的主要控制荷載。其表面風(fēng)荷載具有明顯的三維特征，本征正交分解(POD)方法作為一種有效描述大跨屋面風(fēng)荷載分布狀況的有效工具[3?7]，是空間時(shí)間分離的分析方法。Holmes等[3]應(yīng)用POD分析了脈動(dòng)壓力場(chǎng)。另一方面，大跨度體育場(chǎng)館屋蓋結(jié)構(gòu)本身存在振動(dòng)模態(tài)密集、振型間耦合效應(yīng)明顯等特點(diǎn)，高階模態(tài)對(duì)結(jié)構(gòu)風(fēng)致響應(yīng)不可忽略，甚至部分高階模態(tài)貢獻(xiàn)很大的現(xiàn)象。應(yīng)用以傳統(tǒng)振型分解理論為基礎(chǔ)的頻域分析方法時(shí)，較難有效處理計(jì)算振型數(shù)量和保證必要的計(jì)算精度。眾所周知，衡量1個(gè)振型對(duì)結(jié)構(gòu)動(dòng)力響應(yīng)的程度由下述2個(gè)條件共同決定：1) 振型形狀是否與荷載的空間分布形式類似；2) 該振型對(duì)應(yīng)的頻率與荷載的中心頻率接近程度。由Wilson等[8]提出的WYD (Wilson Yuan Dickens)法所采用的Ritz向量直接疊加法正是根據(jù)這2個(gè)條件來(lái)選擇初始Ritz向量。基于荷載的Ritz向量考慮了荷載的空間分布特點(diǎn)，只需少數(shù)Ritz向量即可保證振動(dòng)響應(yīng)分析精度，從而顯著提高計(jì)算效率。Gu等[9]對(duì)WYD進(jìn)行了改進(jìn)，發(fā)展了與荷載頻率相關(guān)的Ritz向量疊加法，李方慧等[10?13]對(duì)運(yùn)用Ritz法對(duì)大跨屋蓋結(jié)構(gòu)的抗風(fēng)設(shè)計(jì)進(jìn)行了相關(guān)論述。對(duì)于大跨屋蓋風(fēng)致動(dòng)力響應(yīng)分析，Ritz向量疊加法的一個(gè)關(guān)鍵問(wèn)題是如何得到荷載的空間分布形式。通過(guò)本征正交分解法(POD)法，可以用較少的幾組本征模態(tài)作為Ritz模態(tài)分析的初始荷載向量，得到基于風(fēng)荷載POD分解的Ritz模態(tài)振型，進(jìn)行后續(xù)的隨機(jī)振動(dòng)分析[14]。本文以廣州國(guó)際演藝中心大跨度屋蓋為例，在考慮下部混凝土支承體系共同作用下對(duì)其上部大跨度空間屋蓋的風(fēng)致動(dòng)力響應(yīng)進(jìn)行研究。同時(shí)，在用頻域法進(jìn)行的風(fēng)致響應(yīng)計(jì)算中，分別采用多階傳統(tǒng)自由振動(dòng)模態(tài)和數(shù)量較少的基于屋蓋風(fēng)荷載分布特征的塊Ritz向量模態(tài)進(jìn)行分析。

1 工程概況及結(jié)構(gòu)體系

廣州國(guó)際體育演藝中心模型見(jiàn)圖1，它為符合NBA(National basketball association)和AEG(Anschutz entertainment group)標(biāo)準(zhǔn)的大型綜合性體育場(chǎng)館，總建筑面積約 12 萬(wàn)m2，建筑高度為34.5 m。該體育館由屋面鋼結(jié)構(gòu)屋架和下部混凝土主體結(jié)構(gòu)組成(圖1(a))，兩者之間采用具有一定水平滑移和轉(zhuǎn)動(dòng)剛度的橡膠支座連接。上部屋架長(zhǎng)×寬為136 m×106 m的鋼桁架結(jié)構(gòu)，縱橫桁架正交分布，其主要由10榀跨度為79.7~106.2 m、高為8.2~12.1 m的主桁架和兩榀跨度為136.2 m、桁架高為11.8 m的次桁架組成。圖1(b)所示為其上部屋蓋部分的SAP2000有限元模型。下部混凝土結(jié)構(gòu)體系對(duì)上部大跨度鋼結(jié)構(gòu)屋蓋結(jié)構(gòu)的支承作用，采用設(shè)計(jì)單位提供的如表1所示的支承剛度(如圖1(b)中底部支座部分)進(jìn)行模擬。

(a) 廣州體育演藝中心主體育館整體模型；(b) 主體育館上部屋蓋SAP2000有限元模型

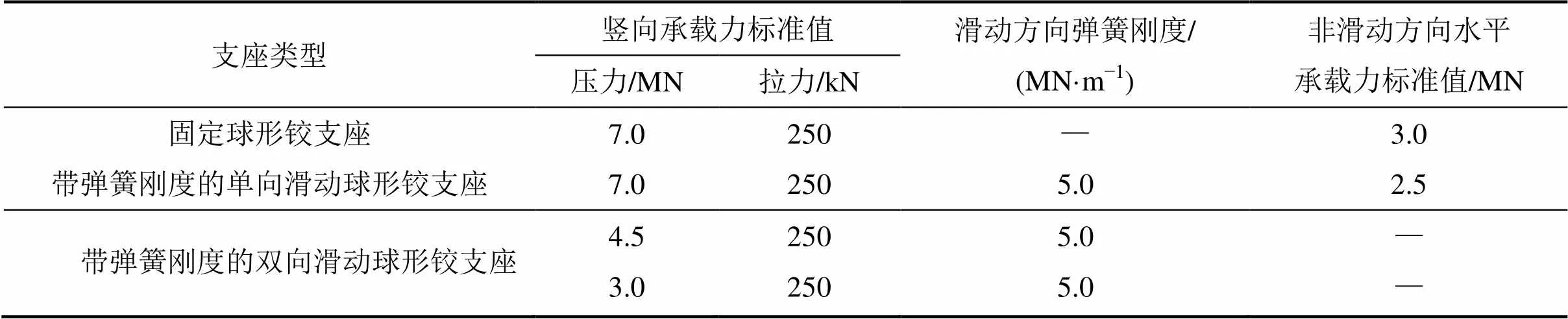
表1 廣州國(guó)際體育演藝中心屋蓋下部支座支承剛度

2 風(fēng)洞實(shí)驗(yàn)概述

新鄉(xiāng)醫(yī)學(xué)院點(diǎn)加團(tuán)隊(duì)結(jié)合自身和本校的實(shí)際情況，在探索“科研團(tuán)隊(duì)——小組二元育人模式”的過(guò)程中，取得諸多成績(jī)的同時(shí)并發(fā)現(xiàn)該模式運(yùn)行中還存在著相關(guān)指導(dǎo)老師配備不足，無(wú)法向全校本科生開(kāi)展培養(yǎng)，監(jiān)督機(jī)制不夠完善，活動(dòng)開(kāi)展形式過(guò)于教條等方面的問(wèn)題。點(diǎn)加團(tuán)隊(duì)還應(yīng)繼續(xù)創(chuàng)新和完善 “科研團(tuán)隊(duì)——小組二元育人模式”的制度，并在高等醫(yī)學(xué)教育改革背景下實(shí)踐和探索本科生科研素質(zhì)培養(yǎng)模式，為地方和國(guó)家培養(yǎng)出具備優(yōu)秀科研素質(zhì)，符合應(yīng)用創(chuàng)新型的人才。

為評(píng)估和分析其上部屋蓋的風(fēng)荷載及風(fēng)致動(dòng)力響應(yīng)，在汕頭大學(xué)風(fēng)洞實(shí)驗(yàn)室進(jìn)行剛性測(cè)壓模型的風(fēng)洞試驗(yàn)。模型的幾何縮尺比為 1:200。試驗(yàn)中以原型地址120 m作為參考高度，以36 個(gè)風(fēng)向角在模擬的B 類地貌湍流邊界層來(lái)流條件中進(jìn)行。確定計(jì)算結(jié)構(gòu)風(fēng)荷載的重現(xiàn)期采用100 a，對(duì)應(yīng)的基本風(fēng)壓分別為0.60 kN/m2，風(fēng)洞試驗(yàn)采樣頻率為312.5Hz。

3 基于Ritz-POD法求解大跨屋蓋的風(fēng)致動(dòng)力響應(yīng)

3.1 本征正交分解法(POD)

本征正交分解法(POD)可以有效地描述大跨屋蓋結(jié)構(gòu)表面風(fēng)壓分布特征，其具體作法為：將已知脈動(dòng)風(fēng)壓向量{()}表示成另一空間狀態(tài)[]，此狀態(tài)使得{()}在{}上的投影值a()最大化。

其中：{}可通過(guò)求解脈動(dòng)風(fēng)壓空間協(xié)方差矩陣的特征值獲取，且滿足均方值條件。

由于均方值反映了脈動(dòng)風(fēng)壓向量{()}中與能量相關(guān)的信息，所以，可以使用本征值來(lái)衡量前幾階模態(tài)所包含的風(fēng)荷載能量，只需根據(jù)少量的前幾階本征模態(tài)便可以較好地描述大跨屋蓋表面脈動(dòng)風(fēng)壓特征。其中，前階本征模態(tài)對(duì)脈動(dòng)風(fēng)壓貢獻(xiàn)的模態(tài)累積率可定義如下：

一般認(rèn)為當(dāng)b大于0.75時(shí)，所取的本征模態(tài)數(shù)目即可滿足要求。

3.2 基于荷載的Ritz模態(tài)分析

Ritz向量疊加法的一個(gè)關(guān)鍵問(wèn)題是如何得到荷載的空間分布形式。對(duì)于大跨度屋蓋的風(fēng)致振動(dòng)響應(yīng)計(jì)算，通過(guò)荷載向量狀態(tài)空間的POD轉(zhuǎn)換，可以用較少的幾組本征模態(tài)作為Ritz模態(tài)分析的初始荷載向量，得到基于風(fēng)荷載POD分解的Ritz模態(tài)振型；運(yùn)用較少的振型再通過(guò)諧波激勵(lì)法[15]便可得到與運(yùn)用較多傳統(tǒng)自由振動(dòng)振型分析法幾乎相同的風(fēng)致響應(yīng)分析精度。

3.3 Ritz-POD法聯(lián)合運(yùn)用求解大跨屋蓋結(jié)構(gòu)的風(fēng)致動(dòng)力響應(yīng)

綜合運(yùn)用POD和基于荷載的Ritz模態(tài)分析結(jié)果，采用隨機(jī)振動(dòng)相關(guān)理論，以SAP2000有限元軟件的MATLAB應(yīng)用程序編程接口環(huán)境(API)，編制大跨屋蓋結(jié)構(gòu)的風(fēng)致動(dòng)力響應(yīng)相關(guān)分析程序，其基本流程見(jiàn)圖2。

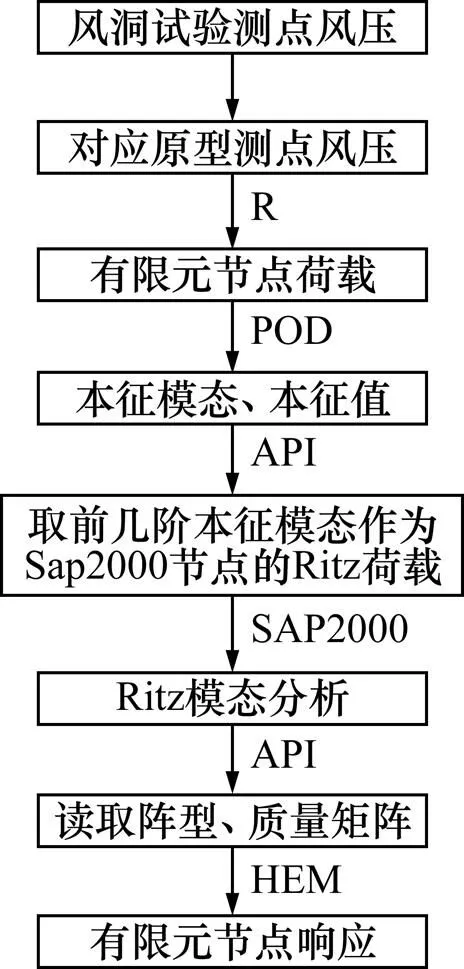
圖2 Ritz-POD法計(jì)算屋蓋風(fēng)致響應(yīng)計(jì)算流程圖

4 Ritz-POD法和傳統(tǒng)模態(tài)分解法求解大跨屋蓋風(fēng)致響應(yīng)結(jié)果對(duì)比分析

以廣州國(guó)際體育演藝中心的上部結(jié)構(gòu)大跨度屋蓋有限元模型為例，結(jié)合風(fēng)洞測(cè)壓實(shí)驗(yàn)得到的表面風(fēng)荷載時(shí)程，用Ritz-POD法和傳統(tǒng)模態(tài)分解法分別求解其風(fēng)致動(dòng)力響應(yīng)。根據(jù)風(fēng)洞測(cè)壓實(shí)驗(yàn)的屋蓋表面脈動(dòng)風(fēng)荷載分布狀況， POD分析中各階對(duì)應(yīng)的模態(tài)累計(jì)貢獻(xiàn)率如圖3所示。從圖3可見(jiàn)：前5階的模態(tài)貢獻(xiàn)率高達(dá)73.64%。因此，選取本征模態(tài)前5階對(duì)應(yīng)的本征模態(tài)向量，作為基于荷載的Ritz模態(tài)分析的初始向量組。在進(jìn)行Ritz模態(tài)分析時(shí)，選用的Ritz模態(tài)階數(shù)為前40階，而傳統(tǒng)模態(tài)分析時(shí)選取的振動(dòng)模態(tài)階數(shù)為前100階。

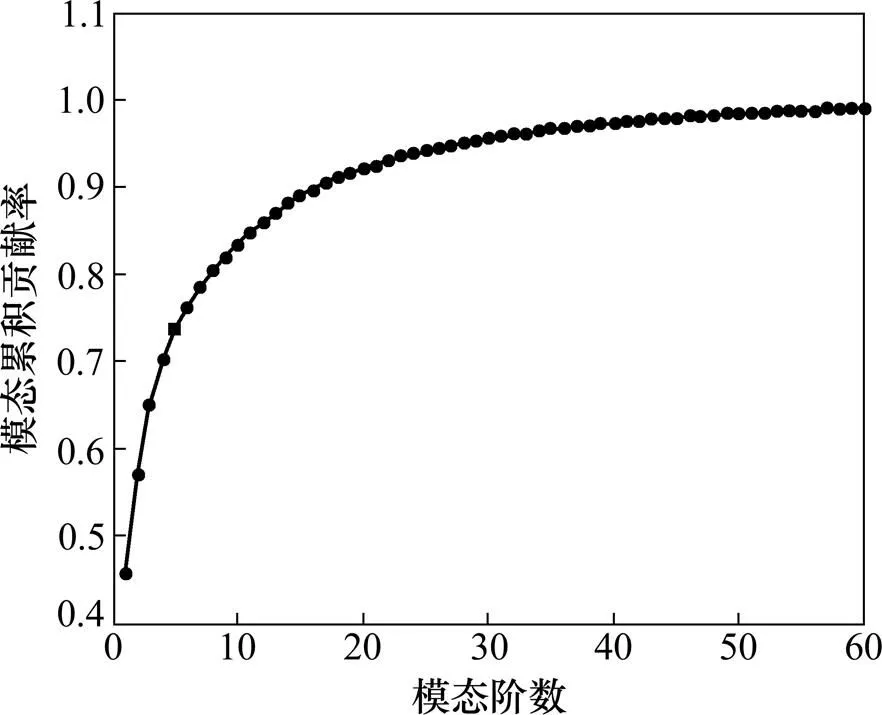
圖3 POD分解法各階模態(tài)累積貢獻(xiàn)率曲線

4.1 水平方向(方向)風(fēng)致位移均方根相應(yīng)對(duì)比分析

對(duì)按傳統(tǒng)模態(tài)分解法和Ritz-POD法求得的上部屋蓋模型，在風(fēng)向角為0°及重現(xiàn)期為100 a時(shí)，求得的各節(jié)點(diǎn)水平方向(方向)風(fēng)致位移均方根分布圖分別見(jiàn)圖4和圖5。從圖4和圖5可見(jiàn)：2種方法中，均方根最大位移均對(duì)應(yīng)有限元節(jié)點(diǎn)221號(hào)，Ritz-POD(Ritz)法對(duì)應(yīng)的最大位移為0.000 170 m，傳統(tǒng)模態(tài)分解法(Modal)對(duì)應(yīng)的最大位移為0.000 163 m。從圖5所示的由2種分析方法所得位移均方根相對(duì)誤差可見(jiàn)，兩者誤差最大出現(xiàn)在有限元節(jié)點(diǎn)611號(hào)，為80.39%；二者誤差最小比值出現(xiàn)在有限元節(jié)點(diǎn)294號(hào)，為?9.62%；而對(duì)于其他大部分節(jié)點(diǎn)，兩者得到的風(fēng)致位移響應(yīng)均大致相同。從圖4和圖5可以看出：Ritz法僅需前40階就可以得到與傳統(tǒng)振型分解法取前100階模態(tài)組合結(jié)果相同的準(zhǔn)確性和精度。

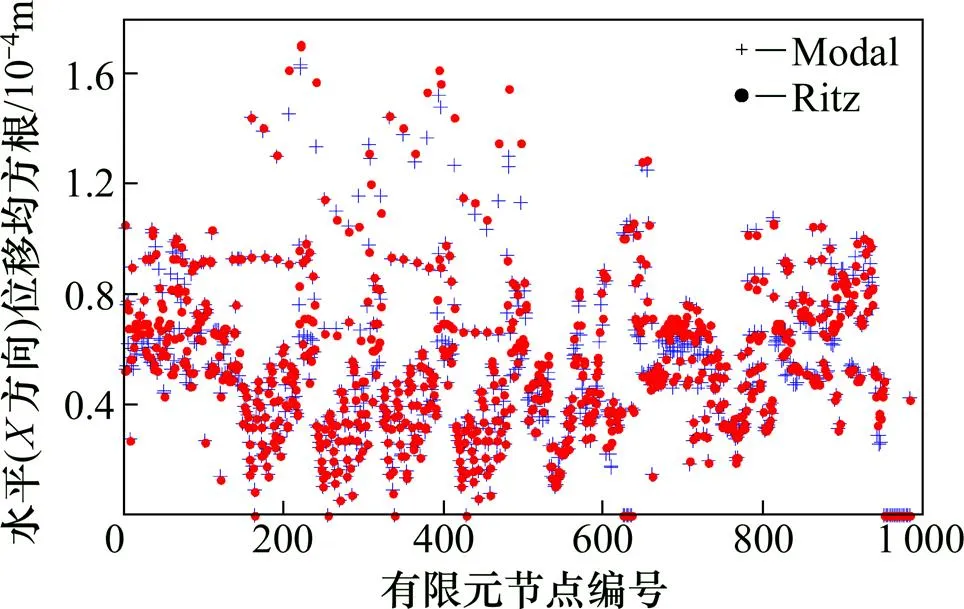
圖4 水平方向(X方向)風(fēng)致位移均方根分布

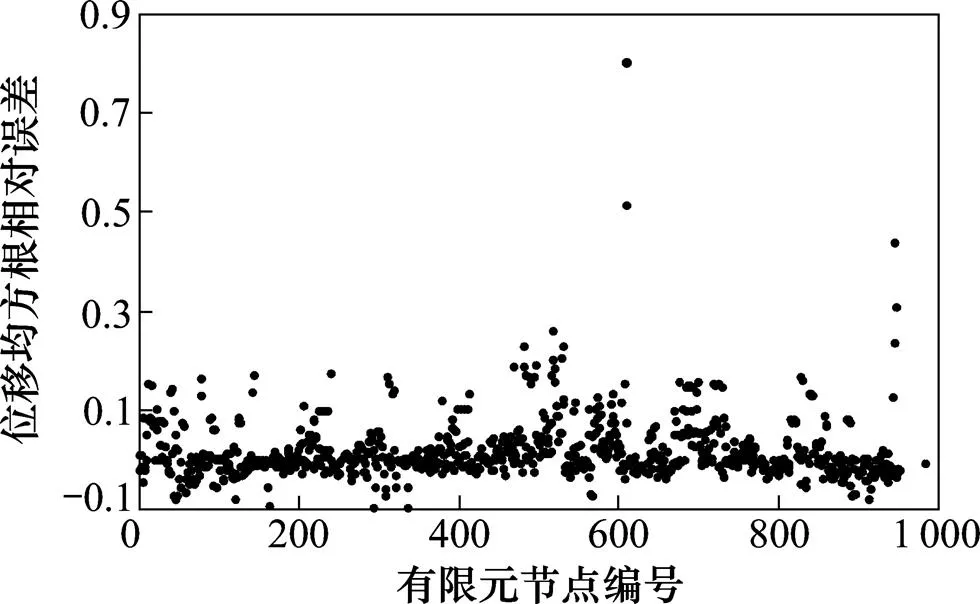
圖5 Modal與Ritz方法水平方向的風(fēng)致位移均方根相對(duì)誤差

4.2 豎直方向(方向)風(fēng)致位移均方根相應(yīng)對(duì)比分析

一般地，大跨度屋蓋結(jié)構(gòu)的最大風(fēng)致位移出現(xiàn)在垂直方向上。圖6所示為傳統(tǒng)模態(tài)分解法和Ritz-POD這2種方法在0°風(fēng)向角及100 a重現(xiàn)期條件下，求得的各節(jié)點(diǎn)豎直方向(方向)風(fēng)致位移均方根分布圖。圖7所示為這2種方法計(jì)算的風(fēng)致位移均方根相對(duì)誤差圖。從圖6和圖7可看出：Ritz-POD(Ritz)法對(duì)應(yīng)的位移最大值為0.002 8 m，傳統(tǒng)模態(tài)分解法的位移最大值為0.003 0 m。從圖7可以看出：2種方法位移誤差最小比值出現(xiàn)在有限元節(jié)點(diǎn)579號(hào)，其值約為?10%，而對(duì)于其他大部分節(jié)點(diǎn)，兩者得到的風(fēng)致位移響應(yīng)值均大致相同。這再一次驗(yàn)證了用Ritz-POD法分析具有密集自振頻率分布的大跨度屋蓋風(fēng)致響應(yīng)是高效和有效的。

圖6 豎直方向(Z方向)風(fēng)致位移均方根分布

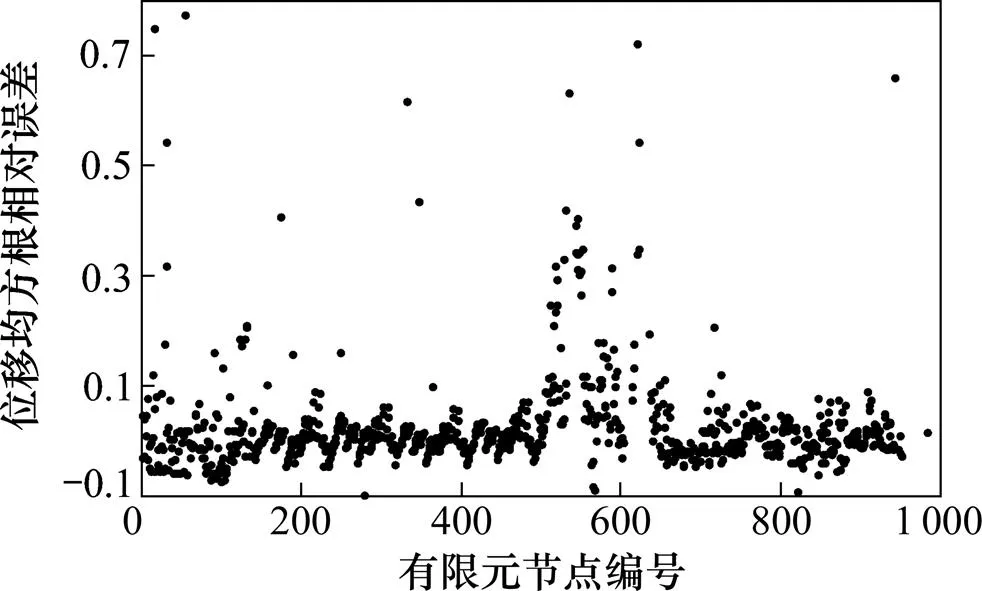
圖7 Modal與Ritz方法豎直方向的風(fēng)致位移均方根相對(duì)誤差

5 考慮下部支撐結(jié)構(gòu)共同作用的大跨屋蓋結(jié)構(gòu)風(fēng)致動(dòng)力響應(yīng)分析

廣州國(guó)際體育演藝中心體育館的整體結(jié)構(gòu)體系由剛度相對(duì)較小的上部大跨空間屋蓋鋼結(jié)構(gòu)和具有較大剛度的下部混凝土結(jié)構(gòu)支承體系共同組成，因此，下面采用2種不同的有限元分析模型進(jìn)行風(fēng)致響應(yīng)對(duì)比分析：1) 將上部大跨鋼屋蓋和下部混凝土支撐結(jié)構(gòu)全部加以考慮(此處稱之為整體模型)，動(dòng)力分析時(shí)所選取的模態(tài)為按傳統(tǒng)自由振動(dòng)分析得到的自由振動(dòng)模態(tài)，模態(tài)階數(shù)為32，其計(jì)算模型如圖8所示；2) 圖1(b)中僅考慮上部屋蓋結(jié)構(gòu)的有限元模型(此處稱之為簡(jiǎn)化整體模型)，但其下部結(jié)構(gòu)的影響用上、下部連接處的支撐剛度(如表1所示)進(jìn)行模擬。動(dòng)力分析時(shí)選用的模態(tài)采用基于Ritz-POD分析的振動(dòng)模態(tài)，Ritz模態(tài)數(shù)目也采用32階，以對(duì)比2種不同計(jì)算模式下鋼結(jié)構(gòu)屋蓋的風(fēng)致動(dòng)力響應(yīng)分析結(jié)果。

圖8 考慮上、下部共同作用的整體結(jié)構(gòu)有限元分析模型

整體有限元分析模型(見(jiàn)圖8)前10階自振頻率及對(duì)應(yīng)的振動(dòng)特征見(jiàn)表2，考慮上、下部共同作用(見(jiàn)圖1(b))的簡(jiǎn)化整體模型見(jiàn)表3。

表2 整體有限元分析模型的前10階自振頻率

表3 大跨屋蓋結(jié)構(gòu)考慮下部支承剛度的前10階Ritz模態(tài)自振頻率

5.1 2種計(jì)算模式在豎直方向(Z方向)風(fēng)致位移均方根對(duì)比分析

采用2種不同的計(jì)算模型，在風(fēng)向角為0°及重現(xiàn)期為100 a時(shí)，求得各節(jié)點(diǎn)豎直方向(方向)風(fēng)致位移均方根分布及兩者相對(duì)誤差分別見(jiàn)圖9和圖10。其中，由于個(gè)別有限元節(jié)點(diǎn)位移遠(yuǎn)大于其余大多數(shù)節(jié)點(diǎn)位移，為避免在相同圖形比例中將其余大多數(shù)節(jié)點(diǎn)位移的信息淹沒(méi)，個(gè)別具有較大節(jié)點(diǎn)位移的響應(yīng)結(jié)果未在圖中顯示(后續(xù)采用同樣處理手法)。整體模型的最大豎向位移出現(xiàn)在有限元節(jié)點(diǎn)502號(hào)，其值為0.776 mm；簡(jiǎn)化整體模型的最大豎向位移出現(xiàn)在節(jié)點(diǎn)94號(hào)，其值為2.8 mm。從圖9和圖10可以看出：這2種計(jì)算模型的風(fēng)致位移分布狀況大致相同。由于簡(jiǎn)化整體模型采用的是基于脈動(dòng)風(fēng)荷載分布的Ritz模態(tài)，而整體模型的是常規(guī)自由振動(dòng)模態(tài)，且這2種模型的模態(tài)數(shù)目均為32階，因此，采用簡(jiǎn)化整體模型得到的絕大部分節(jié)點(diǎn)風(fēng)致動(dòng)力響應(yīng)結(jié)果稍大，兩者相對(duì)誤差大部分集中在?2%~20%之間。

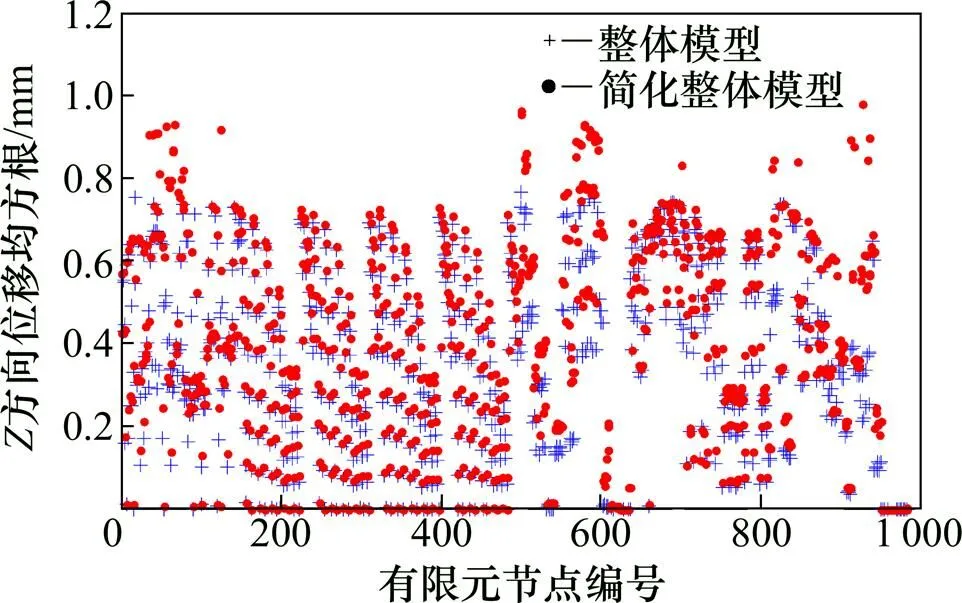
圖9 2種計(jì)算模式下豎直方向(Z方向)風(fēng)致位移響應(yīng)

圖10 整體模型與簡(jiǎn)化整體模型計(jì)算模式下的豎直方向(Z方向)風(fēng)致位移均方根相對(duì)誤差

5.2 2種計(jì)算模式在水平方向(方向)風(fēng)致位移均方根相應(yīng)對(duì)比分析

采用2種不同的計(jì)算模型，在風(fēng)向角為0°及重現(xiàn)期為100 a時(shí)，求得各節(jié)點(diǎn)在水平方向(方向)風(fēng)致位移均方根分布及相對(duì)誤差分別見(jiàn)圖11和圖12。從圖11和圖12可見(jiàn)：整體模型的最大向位移出現(xiàn)在有限元節(jié)點(diǎn)145號(hào)，其值為0.224 mm；簡(jiǎn)化整體模型的最大向位移出現(xiàn)在有限元節(jié)點(diǎn)401號(hào)，其值為0.700 mm。從表2和表3可以看出：簡(jiǎn)化整體模型和整體模型的前10階均以豎向振動(dòng)模態(tài)為主，但在簡(jiǎn)化整體模型的前10階中仍有部分水平側(cè)向振動(dòng)的模態(tài)出現(xiàn)，因此，這2種模型的水平風(fēng)致位移響應(yīng)的誤差比豎向位移響應(yīng)的強(qiáng)度大。從圖12可以看到：兩者相對(duì)誤差大部分集中在20%~50%之間。

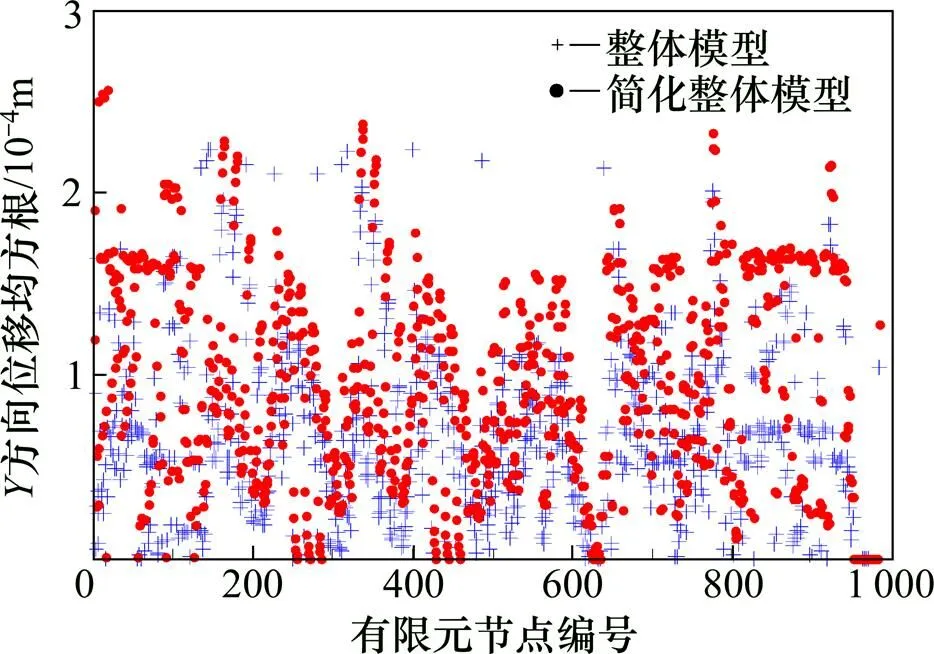
圖11 2種計(jì)算模式下水平側(cè)向方向(Y方向)的風(fēng)致位移響應(yīng)

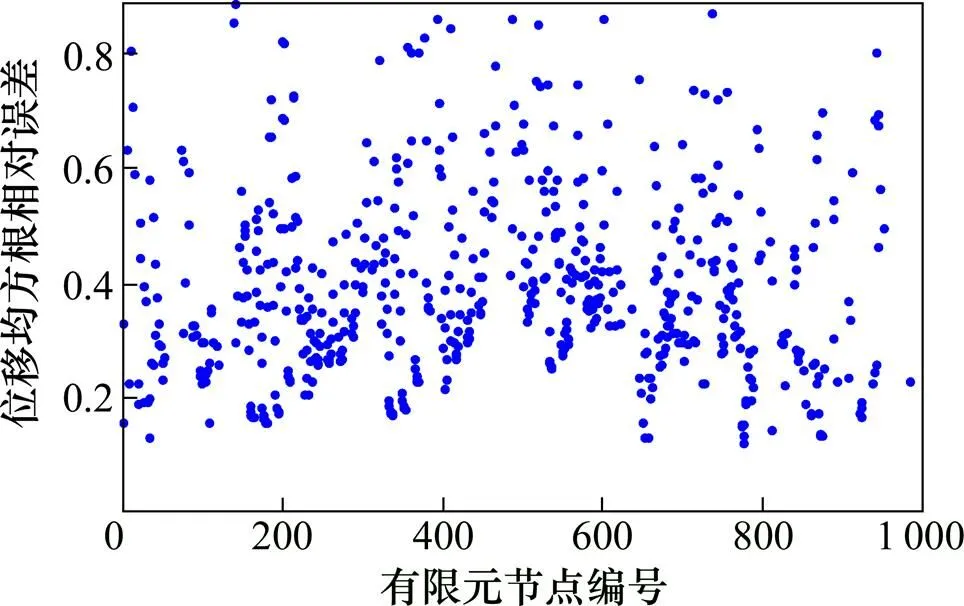
圖12 整體模型與簡(jiǎn)化整體模型計(jì)算模式下的水平側(cè)向方向(Y方向)的風(fēng)致位移均方根相對(duì)誤差

通過(guò)上述2種模型的風(fēng)致動(dòng)力響應(yīng)分析結(jié)果可以看出：采用簡(jiǎn)化整體模型計(jì)算大跨度復(fù)雜屋蓋結(jié)構(gòu)的風(fēng)致動(dòng)力響應(yīng)與采用整體模型相比，一方面，可以通過(guò)上、下部連接處的支承剛度有效地模擬這兩者之間的共同作用，大大減少了有限元分析的工作量；另一方面，在風(fēng)致動(dòng)力響應(yīng)分析中，當(dāng)兩者采用相同數(shù)目的參振模態(tài)時(shí)，簡(jiǎn)化整體模型所包含的對(duì)屋蓋風(fēng)致位移響應(yīng)有直接貢獻(xiàn)的模態(tài)比整體模型的多，因此，采用本文的簡(jiǎn)化整體模型，結(jié)合Ritz-POD模態(tài)分析方法，可以用相對(duì)較少數(shù)目的參振模態(tài)進(jìn)行風(fēng)致動(dòng)力響應(yīng)分析，得到的風(fēng)致振動(dòng)結(jié)果與用整體模型的分析結(jié)果相比略偏大。

6 結(jié)論

1) 采用本文的Ritz-POD方法，可以有效地將POD和基于荷載的Ritz模態(tài)求解方法有機(jī)地結(jié)合在一起，這為具有復(fù)雜表面脈動(dòng)風(fēng)荷載分布和具有密集耦聯(lián)模態(tài)的大跨度空間屋蓋結(jié)構(gòu)的風(fēng)致動(dòng)力響應(yīng)計(jì)算提供了一種高效簡(jiǎn)潔的方法。采用Ritz-POD法僅需前40階，就可以得到與傳統(tǒng)振型分解法取前100階模態(tài)所得分析結(jié)果相同的準(zhǔn)確性和精度。

2) 簡(jiǎn)化整體模型可以通過(guò)上、下部連接處的支承剛度，有效模擬其兩者之間的共同作用。同時(shí)，結(jié)合Ritz-POD模態(tài)分析方法，簡(jiǎn)化整體模型還可以采用數(shù)量較少的Ritz模態(tài)，得到的風(fēng)致振動(dòng)結(jié)果與用整體模型的分析結(jié)果相比略偏大。

[1] Holmes J D. Wind loading of structures[M]. New York: Spon Press, 2001: 163?221.

[2] Yasui H, Marukawa H, Katagir J, et al. Study of wind-induced response of long-span structure[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 83(1/2/3): 277?288.

[3] Holmes J D, Sankaran R, Kwok K C S, et al. Eigenvector modes of fluctuating pressures on low-rise building models[J]. J Wind Eng Ind Aerodyn, 1997, 69/70/71(7/8/9/10): 697?707.

[4] Tamura Y, Suganuma S, Kikuchi H, et al. Proper orthogonal decomposition of random wind pressure field[J]. Journal of Fluids and Structures, 1999, 13(7/8): 1069?1095.

[5] 倪振華, 江棹榮, 謝壯寧. 本征正交分解技術(shù)及其在預(yù)測(cè)屋蓋風(fēng)壓場(chǎng)中的應(yīng)用[J]. 振動(dòng)工程學(xué)報(bào), 2007, 20(1): 1?8. NI Zhenhua, JIANG Zhaorong, XIE Zhuangning. POD technique and its application for predicting wind pressure on roof[J]. Journal of Vibration Engineering, 2007, 20(1): 1?8.

[6] 江棹榮, 倪振華, 謝壯寧. POD 在大跨屋蓋風(fēng)致響應(yīng)計(jì)算中的應(yīng)用[J]. 土木工程學(xué)報(bào), 2007, 40(6): 1?6. JIANG Zhaorong, NI Zhenhua, XIE Zhuangning. Application of POD in wind-induced response analysis of large span roof[J]. Journal of Civil Engineering, 2007, 40(6): 1?6.

[7] 李方慧, 倪振華, 沈世釗. 單層球面網(wǎng)殼結(jié)構(gòu)風(fēng)致響應(yīng)計(jì)算的塊里茲向量法[J]. 振動(dòng)工程學(xué)報(bào), 2007, 20(2): 128?132. LI Fanghui, NI Zhenhua, SHEN Shizhao. Block Ritz method for wind-induced response analysis of single-layer latticed domes[J]. Journal of Vibration Engineering, 2007, 20(2): 128?132.

[8] Wilson E L, Yuan M W, Dickens J M. Dynamic analysis by direct superposition of Ritz vectors[J]. Earthquake Engineering & Structural Dynamics, 1982, 10(6): 1648?1666.

[9] Gu J M, Ma Z D, Hulbert G M. A new load-dependent Ritz vector method for structural dynamics analysis: Quasi-static Ritz Vectors[J]. Finite Elements in Analysis and Design, 2000, 36(3/4): 261?278.

[10] 李方慧. 大跨屋蓋結(jié)構(gòu)實(shí)用抗風(fēng)設(shè)計(jì)[M]. 哈爾濱: 黑龍江大學(xué)出版社, 2008: 32?48. LI Fanghui. The practical wind resistant design of large span roof structures[M]. Harbin: Heilongjiang University Press, 2008: 32?48.

[11] 武岳, 陳波, 沈世釗. 大跨度屋蓋結(jié)構(gòu)等效靜風(fēng)荷載研究[J]. 建筑科學(xué)與工程學(xué)報(bào), 2005, 22(4): 27?31. WU Yue, CHEN Bo, SHEN Shizhao. Equivalent static wind loading analysis of large-span roof structures[J]. Journal of Architecture and Civil Engineering, 2005, 22(4): 27?31.

[12] Nakayama M, Sasaki Y, Masuda K. An efficient method for selection of vibration modes contributory to wind response on dome-like roofs[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 73(1): 31?43.

[13] 胡繼軍, 李春祥, 黃金枝. 網(wǎng)殼風(fēng)振響應(yīng)主要貢獻(xiàn)模態(tài)的識(shí)別及模態(tài)相關(guān)性影響分析[J]. 振動(dòng)與沖擊, 2001(1): 22?28.HU Jijun, LI Chunxiang, HUANG Jinzhi. The identification of dominated contribution vibration modes and modal correlation analysis for wind-induced vibration analysis of reticulated shells[J]. Vibration and Shock, 2001(1): 22?28.

[14] 張建勝, 武岳, 陳波, 等. Ritz-POD法及其在大跨度屋蓋結(jié)構(gòu)風(fēng)振分析中的應(yīng)用[J]. 沈陽(yáng)建筑大學(xué)學(xué)報(bào)(自然科學(xué)版), 2005, 21(6): 603?607.ZHANG Jiansheng, WU Yue, CHEN Bo, et al. A new load-dependent Ritz Vector method for wind-induced response analysis on large span roof structure[J]. Journal of Shenyang Architecture University (Natural Science), 2005, 21(6): 603?607.

(編輯 陳燦華)

Wind-induced response analysis of long-span roof structure with supporting stiffness

CHEN Zhiyong1, PENG Zhenbin1, CHEN Wei2

(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China; 2. Guangzhou Engineering Contractor Group Co. Ltd., Guangzhou 510030, China)

Based on the wind tunnel test data for the surface wind load of Guangzhou International Sport Complex (GISA), the wind-induced response analysis was conducted for the long-span roof steel structure by utilizing different analyzed models (practical and simplified models) and considering the supporting stiffness. Traditional natural vibration mode shapes and load-dependent Ritz mode shapes were utilized in the frequency domain analysis on the wind-induced response of the long-span roof structure. The initial load vectors for load-dependent Ritz mode analysis were selected from the first five eigenvectors in the POD (proper orthogonal decomposition) decomposition on the covariance matrix of fluctuated wind loads on the long-span roof. The results show that with the combined application of Ritz-POD method, the simplified roof structure model with less Ritz modal shapes obtains larger values in the wind-induced response than those obtained by the practical model does. The simplified model with Ritz-POD algorithm can be supplied as an effective method for the wind-induced response analysis on such complex roof structures.

long span roof structure; wind-induced response; Ritz vector; POD decomposition

10.11817/j.issn.1672-7207.2015.04.039

TU317.2；TU311.3

A

1672?7207(2015)04?1475?07

2014?05?12；

2014?07?22

國(guó)家自然科學(xué)基金資助項(xiàng)目(51378134)(Project (51378134) supported by the National Natural Science Foundation of China)

陳智勇，博士研究生，從事地質(zhì)與結(jié)構(gòu)工程研究；E-mail：kfqczy@163.com