側風下橋上高速列車傾覆穩定性及臨界車速的參數化研究

項超群，郭文華, 2，顏俊卿，張佳文

?

側風下橋上高速列車傾覆穩定性及臨界車速的參數化研究

項超群1，郭文華1, 2，顏俊卿1，張佳文1

(1. 中南大學土木工程學院，湖南長沙，410075;2. 中南大學高速鐵路建造技術國家工程實驗室，湖南長沙，410075)

基于計算流體動力學理論，采用數值模擬的方法計算高速列車通過雙線簡支箱梁橋時的氣動力系數，考慮列車在編組中的位置、迎風側和背風側線路以及風偏角等因素的影響，并將數值模擬結果與風洞實驗進行對比分析。根據列車傾覆系數的定義，推出對傾覆臨界狀態合力作用線與兩側輪軌接觸斑連線交點的累計力矩計算式，從而避免求輪軌相互作用力，直接得到車速和風速的相關表達式，并據此得到求臨界車速的計算方法，最后對影響列車傾覆穩定性的參數進行分析。研究結果表明：采用數值模擬計算的列車氣動力系數與風洞實驗結果較吻合；雙線簡支箱梁橋上迎風側線路頭車所受氣動力最大，其側傾臨界車速最低；隨彈簧剛度系數、線路曲線半徑、軌道超高以及列車質量的增加，臨界車速均會增加，不考慮豎向振動加速度將會過高地估計列車側傾臨界車速。

氣動力系數；傾覆穩定性；臨界車速；高速列車；雙線鐵路橋

近年來，中國在提高既有鐵路運行速度的同時，建設快速和高速客運專線也取得了舉世矚目的成就。隨著對運行安全性、穩定性、行車舒適性以及低能耗、低噪音等要求的不斷提高，對列車氣動性能的研究變得越來越重要，其中側風對列車傾覆穩定性的作用更是不容忽視。運行在強側風作用下的列車將受到很大的氣動側力、升力和側傾力矩作用，在氣動力和其他多種因素綜合作用下列車可能發生脫軌、傾覆等嚴重事故，且隨著列車運行速度的不斷提高，氣動力的作用將更加顯著，強側風對其造成的安全性威脅也大大增加。由于高速鐵路跨越區域較廣，不可避免地要跨越大江大河以及峽谷上的橋梁，當列車運行于橋梁上時，其所受的氣動力遠比地面環境的大，因而列車橫風穩定性大大下降，且國外曾出現過大風將列車吹翻墜橋的事故[1?3]。列車在側風下的臨界車速能從靜平衡方程中得到，因此，為了建立側風作用下的平衡方程，首先必須得到作用在列車上的氣動力[4]。郗艷紅等[5]計算了高速列車在不同側風環境下所受到的氣動力，并采用三次多項式對氣動力與風向角之間的關系進行了回歸分析。劉志燕[6]分析了高速列車在橋梁上的氣動特征，并與在平坦路段的氣動力進行了對比，發現高速列車行駛在橋梁上時傾覆危險性將增大。張杰[7]采用數值模擬的方法，選用南京長江大橋橋體截面形狀，研究了多種截面參數下的側傾力矩，最后對不同環境不同風向角下的氣動力進行了對比，并依此判斷列車在橫風下的穩定性。以上研究只對列車的氣動力進行了分析，蔣崇文等[8]則定義了平原上空載集裝箱所受翻滾力矩與自身重力矩相等時的風速為傾覆臨界風速，計算了某一車速下不同風速等級時列車的氣動力，并與重力矩進行對比從而判斷橫風穩定性。許士軍[9]計算了不同路況下動車組受到的氣動力，推導了橫風作用時車輛傾覆穩定性計算關系式，從而可以考慮車體橫向振動加速度、曲線半徑等更多因素的影響。高廣軍等[10?13]以蘭新線、青藏線上運行的列車為工程背景，對集裝箱整車傾覆穩定性和集裝箱在平車上的傾覆穩定性、氣動力和垂向動載荷等對雙層集裝箱平車臨界車速的影響等進行了研究。為了保證列車的運行安全，常采取運行管制等措施，即在各風速下規定列車能安全運行的臨界車速。由此可見，對強側風作用下列車運行管制與運行效率之間存在一定的矛盾，臨界車速評估偏低而頻繁的運行管制會造成大量列車停運或晚點；反之，則會使列車發生危險的概率大大增加。高速列車采用二系懸掛，當受到外荷載作用時，車體、轉向架等結構將產生位移，已有的研究一般未考慮該位移對側傾力矩力臂的影響，或者只考慮了車體和轉向架之間的位移而忽略了轉向架和輪對之間產生的位移，同時，已有的研究大多未單獨考慮輪對質量等的影響。采用更精確的計算模型計算高速列車在橫風作用下的穩定性具有重要的意義。本文作者基于大型計算流體力學通用軟件FLUENT，采用數值模擬方法計算雙線簡支箱梁橋上列車的氣動力系數，考慮列車在橋上的橫向位置、列車在編組中的位置、來流風偏角等主要因素的影響，并將部分結果與風洞實驗結果進行對比。根據列車傾覆系數的定義，推出具有兩系懸掛系統的高速列車側傾力矩平衡關系式，據此得到計算臨界車速的方法并編制相應的Fortran程序。最后分析彈簧剛度系數、豎向振動加速度、線路曲線半徑、軌道超高以及列車質量等參數對臨界車速的 影響。

1 列車氣動性能

1.1 數值模擬方法

橋梁幾何模型采用32 m雙線簡支箱梁，橋墩對列車的氣動力影響很小，在計算模型中忽略其影響。由于列車中間車輛采用同一截面形式，當氣流流過車頭一定距離后，繞流邊界層結構已趨于穩定，中間車輛的氣動力特性基本一致，因此，在數值模擬中采用包括頭車、中車和尾車的3節車模型，列車均勻段寬3.28 m，高3.82 m。在強側風作用下列車的氣動力問題為三維湍流問題，一般在該問題中不考慮空氣密度的變化，而將流場看作是不可壓縮的[14]。采用合成風法計算橋上列車所受氣動力[11]，即輸入的實際風速為側風風速和列車風速的矢量合成。選用基于有限體積法的CFD軟件FLUENT計算氣動力，因為列車橋梁氣動系統的復雜性，對整個計算域采用四面體的非結構化網格進行離散。入口選用速度入口邊界，出口選用壓力出口邊界，湍流強度取0.5%。橋梁、列車表面均選用無滑移的壁面邊界[6]。為了便于與風洞實驗結果進行對比，車橋數值模型采用1:20的縮尺比。采用RNG?湍流模型，壓力速度場采用SIMPLE算法耦合。

1.2 氣動力系數計算結果

側風和列車風共同作用引起的氣動側力、升力和側傾力矩是使列車吹翻、脫軌等事故發生的主要原 因[15]。氣動力和氣動力矩除了與合成速度有關外，還與風偏角有直接關系[14]，在此定義列車的側力系數、升力系數和側傾力矩系數如下：

式中：s，l和c分別為氣動側力、升力和側傾力矩，力矩作用點為列車截面重心；為空氣密度，計算中取1.225 kg/m3；為相對于列車的實際風速(見圖1)；和分別為側風風速和列車運行速度，計算中假設側風垂直于橋梁軸線；風偏角；參考面積；為列車均勻段高度；為對應車輛長度；f為列車均勻段寬度。

圖1 合成風計算簡圖

對于雙線簡支箱梁橋，當列車處于不同線路時，列車橋梁的相對位置不同，對氣流的擾動也不同，故需分別計算列車處于迎風側線路和背風側線路時的氣動力。通過改變邊界條件計算了風偏角從0°~90°的各種工況，見圖2。從圖2可知：頭車的側力系數、升力系數和側傾力矩系數均比中車和尾車的大；除尾車的升力系數外，列車在迎風側線路上的氣動力系數均比在背風側線路的大；頭車的側力系數、升力系數和側傾力矩系數以及中車的側傾力矩系數均不是風偏角的單調函數，其極值在風偏角[50°, 80°]內。

(a) 側力系數；(b) 升力系數；(c) 側傾力矩系數

1.3 數值模擬與風洞試驗結果對比

在中南大學高速鐵路建造技術國家工程實驗室進行了列車?橋梁系統1:20縮尺模型在風偏角[0°, 50°]內的風洞實驗。為了驗證數值模擬的正確性，選取迎風側線路頭車對比氣動力系數數值模擬結果和風洞實驗結果，見圖3。從圖3可知：氣動力系數計算結果與實驗結果基本吻合，但也存在一定差異。造成該差異的主要原因有：1) 數值模型中受計算網格尺寸的限制，3節車相鄰之間沒有間隙，而在風洞實驗中，為了在測力天平采集氣動力時不受相鄰車輛干擾而相距了微小距離；2) 數值模型和風洞實驗的邊界條件難以完全一致；3) 在風洞實驗中采用三跨簡支梁，因此，列車頭、尾部的箱梁補償段是有限的，而在數值模型中充分考慮了箱梁補償段的影響，橋梁的長度遠大于列車編組的長度；4) 數據采集的時間是有限的，脈動成分對時均結果有影響，而數值模擬中采用定常的計算方法。由此可見：數值模擬結果與風洞實驗結果存在的誤差難以完全消除。本文數值和實驗所得側力系數的平均相對誤差為0.043，升力系數的平均相對誤差為0.056，側傾力矩系數的平均相對誤差為0.047，可認為計算結果可靠。

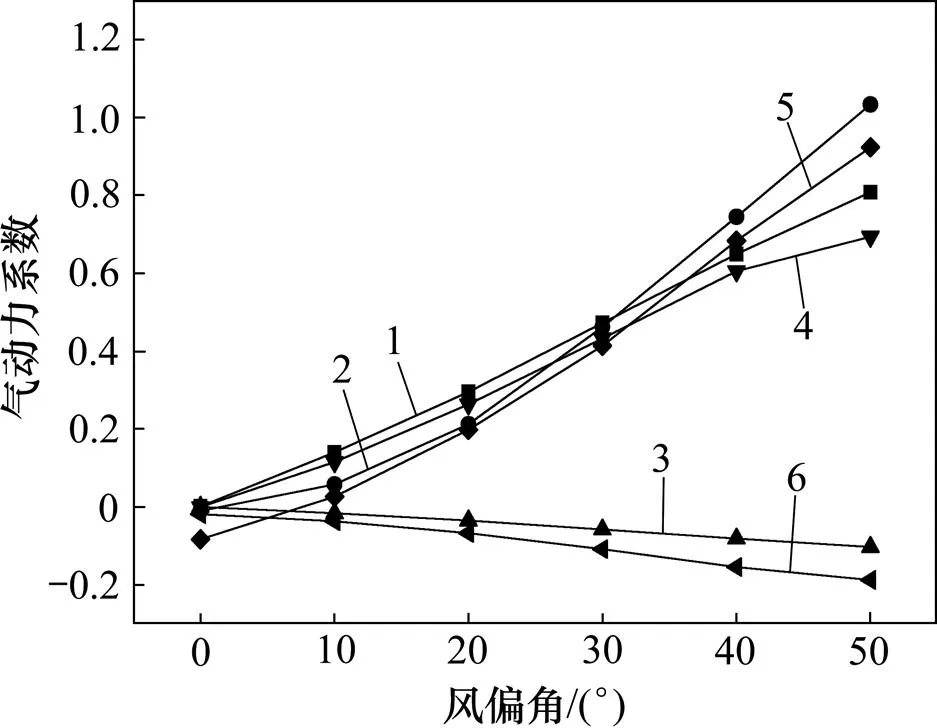
1—側力系數數值模擬結果；2—升力系數數值模擬結果；3—傾側力矩系數數值模擬結果；4—側力系數風洞實驗結果；5—升力系數風洞實驗結果；6—傾側力矩系數風洞實驗結果

2 列車傾覆臨界狀態力學模型

車輛沿曲線軌道運行時，一般受到風力、離心力、重力、車鉤力以及橫向和豎向振動慣性力等作用，由于線路曲線半徑遠大于車體長度，車鉤力產生的橫向力矩可以忽略不計，因此，計算列車傾覆穩定性時往往不考慮車鉤力的作用。在外力的綜合作用下將造成車輛的一側車輪減載，另一側車輪增載，在最不利組合作用下，減載側車輪的輪軌垂向力將減少到0 N，此時，車輛處于傾覆的臨界狀態。車輛可能傾覆的程度用傾覆系數表示[16]：

式中：1為減載側輪軌垂向力；2為增載側輪軌垂向力。為了保證車輛的安全性，GB 5599—1985規定傾覆系數不能超過容許值[]，即≤[]=0.8。

在圖4中，傾覆臨界狀態下右側車輪增載時，輪對、轉向架和車體除輪軌相互作用力以外的所有外荷載合力通過輪軌接觸點連線的右側點，因合力的橫向分量不影響輪軌垂向力，因而對傾覆系數無影響，圖中只表示出車輛垂向的合力sumv。

圖4 輪軌垂向作用力

在圖4中，根據靜力平衡可知：

將式(5)聯合式(4)可得：

若車輛高速通過曲線，而且風力、橫向振動慣性力方向與離心力方向一致，則車輛可能向曲線外側傾覆。忽略轉向架和輪對的氣動力、橫向和豎向振動慣性力以及車鉤力等的影響，彈簧?剛體車輛模型所受外荷載如圖5所示。圖5中：s為氣動側力；l為氣動升力；c為對車體重心的氣動力矩，根據式(1)~(3)所得系數即可求得；，，分別為車體橫向、豎向振動慣性力；車體橫向振動加速度(其中1=9.8 m/s2)；車體豎向振動加速度；c為車體質量；，為車體重力；，為車體離心力；為線路的曲線半徑；，，分別為轉向架重力和離心力；b為單個轉向架的質量；，，分別為輪對重力和離心力；w為單個輪對的質量。wrvl和wrvr分別為左、右側輪軌垂向作用力；wrhl和wrhr分別為左、右側輪軌橫向作用力。

圖5 車輛受力模型

3 列車臨界車速求解方法

車體由彈簧等與轉向架連接，在外荷載作用下將產生橫向和豎向的位移。為計算車體相對于轉向架的位移，對車體進行受力分析：

式中：kb和kb分別為第一系懸掛系統橫向和豎向彈簧剛度系數；1為第一系懸掛系統中央豎向彈簧橫向間距之一半；1為車體重心到中央橫向彈簧的距離。同理，對轉向架進行受力分析，可得

式中：2為中央橫向彈簧到轉向架重心的距離。轉向架相對于輪對的位移可表示為

式中：kt和kt分別為第二系懸掛系統橫向、豎向彈簧剛度系數；3為轉向架重心到軸箱橫向彈簧的距離；2為第二系懸掛系統軸箱豎向彈簧橫向間距之一半。

計算所得車體的位移是相對于轉向架的位移，在線彈性的假設條件下，車體的最終位移需疊加轉向架的位移，即

由輪軌相互作用力可知：wrvl和wrvr對點的力矩互相平衡，wrhl和wrhr對點的力臂長度為0 m，因此，其力矩也為0 N?m。將輪對、轉向架和車體當成一個整體進行分析，圖5中除輪軌相互作用力以外的所有外荷載對點的順時針方向累計力矩可表示為

其中：4為車輪滾動圓半徑。當列車處于傾覆的臨界狀態(=[])時，其所受的所有外荷載對點的力矩之和應為0 N?m，即

M=0 (13)

列車所受氣動力由相對風速和氣動力系數共同決定，且氣動力系數是風偏角的函數，而相對風速和風偏角都必須根據車速和風速才能確定，同時，M的計算中和均為氣動力的函數，因此，由式(13)得不出臨界狀態時車速和風速的顯式表達式。在某一風速下，隨列車運行速度提高，其傾覆可能性隨之增大，故可通過逐步增大車速的試算法找到臨界車速。由上可知，臨界狀態時合力作用線通過點、累計力矩M=0 N?m，當列車速度小于臨界車速時，合力作用線位于點內側、累計力矩小于0 N?m，而當車速大于臨界車速時合力作用線位于點外側、累計力矩大于0 N?m。據此，可按如下步驟編制計算列車在不同風速下的臨界車速Fortran程序：

1) 設置需計算的風速范圍[min,max]和風速增長步長。

2) 設置某較小的車速初始值0和車速增長步長，要求＜2.0(其中，為求解臨界風速的誤差限值)。

3) 由當前風速u和當前車速v計算風偏角，據圖中列車氣動力系數曲線，通過插值得到對應的側力系數、升力系數和側傾力矩系數，進而得到列車氣動力。計算列車受到氣動力等作用后產生的位移，最后根據式(12)計算對點的累計力矩M。

4) 若M＜0，則，重復步驟3)；若M≥0，則風速u對應的臨界車速即為，重置；若u+1＞max，則退出循環，否則，重復步驟2)。

4 累計力矩特性及臨界車速參數分析

根據走行線路，列車傾覆一般有以下3種情況：向曲線外傾覆、向曲線內傾覆和在直線上傾覆。高速列車通過曲線線路時將受到很大的離心力作用，當氣動力和離心力作用一致時，列車最可能向曲線外側傾覆[11, 15]。在側風作用下，列車傾覆穩定性的影響因素較多，針對列車向曲線外側傾覆，假定傾覆系數=0.8，其他計算參數如表1所示[18]。首先以迎風側線路頭車為例，研究累計力矩M隨車速的變化規律，之后分別對不同參數對臨界車速的影響進行分析。

表1 計算參數

4.1 累計力矩特性分析

以迎風側線路頭車為例，車速增長步長為1.0 km/h，計算風速分別為10.0，20.0，30.0和40.0 m/s，車速為0~500.0 km/h時對點的累計力矩見圖6。從圖6可知：1) 對于特定的風速，當車速較小時M為負數，隨車速增大M單調遞增，且均能得到M=0 N?m的點。由前所述，該點橫坐標即為當前風速下的臨界車速，如當側風速度為20.0 m/s時，臨界車速為320.0 km/h；2) 隨著風速的增加，M=0 N?m的點逐漸向橫軸負方向移動，即隨著風速的增加臨界車速下降。

u/(m·s?1)：1—10；2—20；3—30；4—40

4.2 列車臨界車速參數分析

設置風速范圍為5~40.0 m/s，風速增長步長?= 2.5 m/s，車速初始值0=0 km/h，車速增長步長?=1.0 km/h，對影響列車臨界車速的各參數進行分析。

4.2.1 氣動力系數對臨界車速的影響

為了研究列車編組位置以及在橋上的橫向位置對列車傾覆穩定性的影響，計算兩線路上不同風速下3節車的臨界車速，結果見圖7。從圖7可知：1) 列車編組中頭車臨界車速最小，尾車臨界車速最大且隨風速增大而變小的趨勢相對較緩；2) 迎風側列車的臨界車速均比背風側的低，且兩線路上臨界車速差值隨風速變化較小；3) 對于運行于雙線簡支箱梁橋上的列車，迎風側線路上頭車臨界車速起控制作用。為此，在以下研究中均只針對該節車進行分析。

1—迎風側頭車；2—迎風側中車；3—迎風側尾車；4—背風側頭車；5—背風側中車；6—背風側尾車

4.2.2 彈簧剛度系數對臨界車速的影響

研究強側風作用下列車的臨界車速，一般將輪對、轉向架和車體視為剛體，剛體之間通過彈簧等元件相互連接，因此，彈簧元件的剛度系數對列車臨界車速有直接影響。將列車橫向和豎向彈簧剛度同時乘以0.1，1.0和10.0倍，計算各風速下列車的臨界車速，結果見圖8。從圖8可知：1) 彈簧剛度系數越大，臨界車速越高，但臨界車速并不與剛度系數呈線性關系，將當前彈簧剛度系數乘以10.0倍時其臨界車速提高較小，而將其乘以0.1倍時臨界車速急劇下降；2) 隨著風速提高，臨界車速呈近似線性下降，但不同彈簧剛度系數下的臨界車速差值隨風速增大而逐漸變小；3) 當不考慮彈簧的影響而將車輛、轉向架和輪對整體看成一個剛體時，計算所得的臨界車速略偏高。

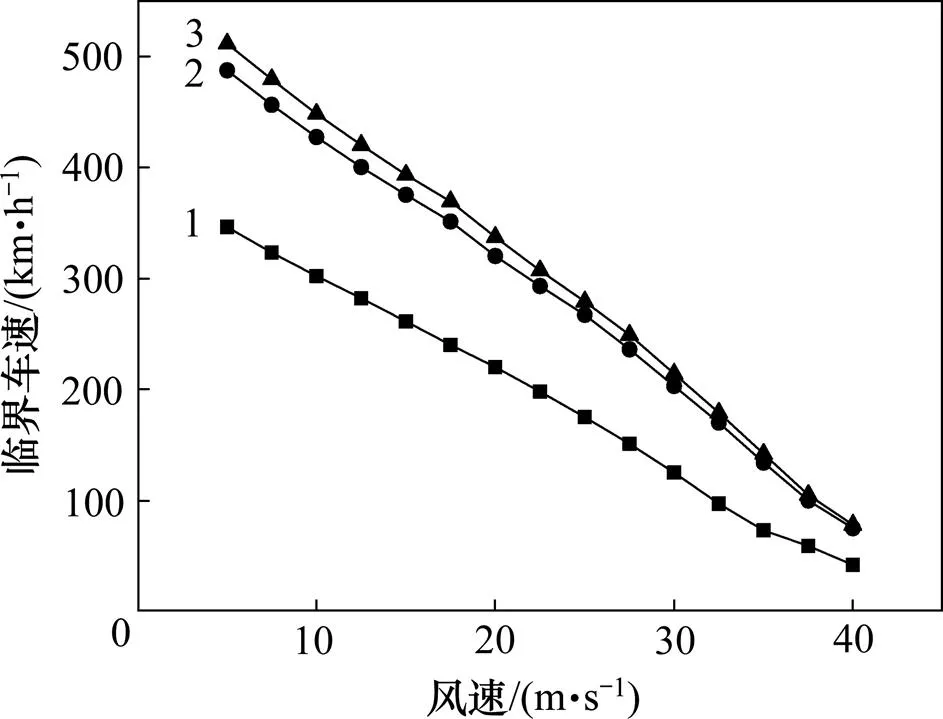
1—0.1倍剛度系數；2—1.0倍剛度系數；3—10.0倍剛度系數

4.2.3 豎向振動加速度對臨界車速的影響

對側風作用下列車的傾覆穩定性進行分析時，一般沒有考慮豎向振動加速度的影響，為此，計算考慮/不考慮豎向振動加速度時的臨界車速，見圖9。從圖9可知：不考慮豎向振動加速度將會過高地估計臨界車速，且差值隨風速變化不敏感，一般為20.0~25.0 km/h。

ay：1—0.13g；2—0

4.2.4 線路曲線半徑對臨界車速的影響

線路曲線半徑對離心力有重要影響，計算曲線半徑分別為4，7和10 km時列車的臨界車速見圖10。從圖10可知：1) 當風速較小時，列車能快速通過曲線，故影響列車傾覆穩定性的各因素中離心力占有很大比例，從而曲線半徑對臨界車速的影響很明顯。曲線半徑為10 km時臨界車速提高了16.6%，曲線半徑為4 km時則降低了22.2%；2) 隨著風速提高，氣動力對列車傾覆穩定性的影響越來越大，而離心力的影響逐步變小，從而臨界車速下降且線路半徑的影響也逐漸減小。

R/km: 1—4；2—7；3—10

4.2.5 軌道超高對臨界車速的影響

為了減少列車通過曲線時旅客經受的離心加速度和輪軌之間的相互作用力，一般在外軌上設置超高，而內軌保持原來高度不變。存在超高時，重力、離心力等對于固定于列車上的坐標軸將有一夾角(見圖5)，從而影響側風作用下列車的傾覆穩定性。計算超高分別為100，150和200 mm時列車的臨界車速，結果見圖11。從圖11可知：當采用較大的超高值時，列車的臨界車速增大，且不同超高值間臨界車速差值隨風速變化較小。

h/mm：1—100；2—150；3—150

4.2.6 列車質量對臨界車速的影響

隨著輕質高強復合材料的廣泛使用，列車的質量不斷減小，這對提高列車加速性能、降低能耗等是有利的，但由此也導致列車在側風下側傾性能發生改變。計算將整車質量分別乘以0.75，1.00和1.25倍時的臨界車速見圖12。從圖12可知：列車臨界車速隨質量的增加而增加，且隨著風速提高，列車質量對臨界車速的影響逐漸增大；當風速40.0 m/s時，1.25倍整車質量時臨界車速提高72%，0.75倍整車質量時則降低68%。

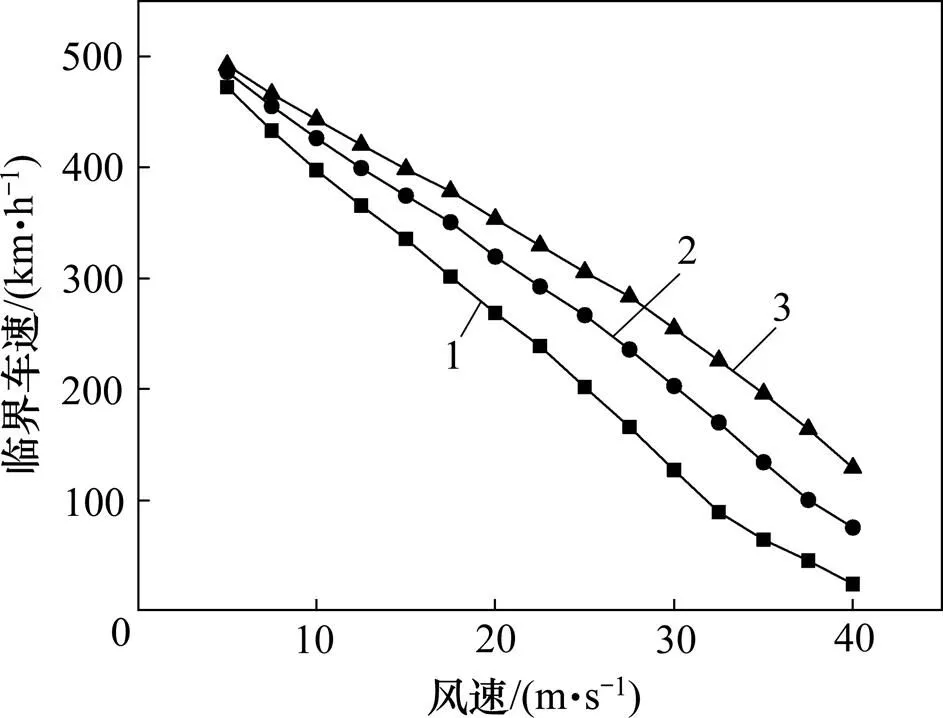
1—0.75倍質量；2—1.00倍質量；3—1.25倍質量

5 結論

1) 對于雙線簡支箱梁橋，在強側風作用下，當列車處于迎風側線路時所受的氣動力比背風側的大。在列車編組中，頭車所受氣動力比中車和尾車的大。計算強側風下雙線簡支箱梁橋上列車傾覆穩定臨界車速時，迎風側頭車起控制作用。

2) 采用數值模擬計算強側風作用下列車的氣動力系數基本可靠，但引起數值模擬和風洞實驗結果差異的原因仍較多，如數值模型和風洞實驗模型不完全一致、風洞實驗數據采集和處理、數值模擬中參數的設置等。

3) 根據傾覆系數的定義，推出了對傾覆臨界狀態合力作用線與兩側輪軌接觸斑連線交點的累計力矩計算式，從而不必求輪軌垂向力和橫向力的具體數值，而通過逐步增大車速的方法直接得到指定風速下的臨界車速。

4) 高速列車采用二系懸掛系統，計算傾覆穩定性時應考慮強側風等作用下產生的橫向和垂向位移，過高地估計彈簧剛度系數甚至采用不考慮彈簧作用的剛體模型將會使計算所得的臨界車速偏高。

5) 影響側風作用下列車傾覆穩定性的因素較多。不考慮車體豎向振動加速度的作用將會過高地估計列車的臨界車速，隨線路曲線半徑、軌道超高以及列車質量的增加，臨界車速均會增加。

[1] Fujii T, Maeda T, Ishida H, et al. Wind-induced accidents of train/vehicles and their measure in Japan[J]. Quarterly Report of Railway Technical Research Institute, 1999(1): 50?55.

[2] 劉慶寬, 杜彥良, 喬富貴. 日本列車橫風和強風對策研究[J]. 鐵道學報, 2008, 30(1): 82?88. LIU Qingkuan, DU Yanliang, QIAO Fugui. Train-crosswind and strong wind countermeasure research in Japan[J]. Journal of the China Railway Society, 2008, 30(1): 82?88.

[3] Raghunathan R S, Kim H D, Setoguchi T. Aerodynamics of high-speed railway train[J]. Progress in Aerospace Sciences, 2002, 38: 469?514.

[4] Suzuki M, Tanemoto K, Maeda T. Aerodynamic characteristics of train/vehicles under cross winds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91: 209?218.

[5] 郗艷紅, 毛軍, 張念. 強風中高速列車安全性研究[J]. 中國安全科學學報, 2010, 20(5): 39?45. XI Yanhong, MAO Jun, ZHAGN Nian. Study on the safety of high-speed train in strong wind[J]. China Safety Science Journal, 2010, 20(5): 39?45.

[6] 劉志燕. 側風下高速列車?簡支箱梁系統氣動性能的數值研究[D]. 長沙: 中南大學土木工程學院, 2010: 34?36. LIU Zhiyan. The numerical study of aerodynamic character of high-speed train and simply supported box girder under side wind[D]. Changsha: Central South University. School of Civil Engineering, 2011: 34?36.

[7] 張杰. 行駛環境對高速列車橫風穩定性影響研究[D]. 上海: 同濟大學汽車學院, 2009: 38?68. ZHAGN Jie. Study on the effect of running environment to crosswind stability of high-speed train[D]. Shanghai: Tongji University. School of Automotive Studies, 2009: 38?68.

[8] 蔣崇文, 張勁柏, 關雪梅, 等. 橫風強度對平原上集裝箱列車橫向穩定性的影響[J]. 鐵道學報, 2011, 33(3): 17?22. JIANG Chongwen, ZHANG Jinbai, GUAN Xuemei, et al. Influence of crosswind intensity on cross stability of container trains running on plain[J]. Journal of the China Railway Society, 2011, 33(3): 17?22.

[9] 許士軍. 橫風環境下動車組傾覆穩定性研究[D]. 長沙: 中南大學交通運輸工程學院, 2009: 15?34. XU Shijun. Study on capsizing stability of EMU in crosswind[D]. Changsha: Central South University. School of Traffic and Transportation Engineering, 2009: 15?34.

[10] 高廣軍. 強側風作用下列車運行安全性研究[D]. 長沙: 中南大學軌道交通安全教育部重點實驗室, 2009: 39?57. GAO Guangjun. Research on train operation safety under strong side wind[D]. Changsha: Central South University. Key Laboratory of Traffic Safety on Track, Ministry of Education, 2009: 39?57.

[11] 高廣軍, 李鵬. 青藏線上集裝箱平車在強橫風下的穩定性[J]. 中南大學學報(自然科學版), 2011, 42(2): 533?538. GAO Guangjun, LI Peng. Running stability of container car in Qinghai—Tibet railway line[J]. Journal of Central South University (Science and Technology), 2011, 42(2): 533?538.

[12] 高廣軍, 田紅旗, 張健. 橫風對雙層集裝箱平車運行穩定性的影響[J]. 交通運輸工程學報, 2004, 4(2): 45?48. GAO Guangjun, TIAN Hongqi, ZHANG Jian. Crosswind affection on double container train[J]. Journal of Traffic and Transportation Engineering, 2004, 4(2): 45?48.

[13] 高廣軍, 田紅旗, 姚松, 等. 蘭新線強橫風對車車輛傾覆穩定性的影響[J]. 鐵道學報, 2004, 26(4): 36?40. GAO Guangjun, TIAN Hongqi, YAO Song, et al. Effect of strong crosswind on the stability of trains running on the Lanzhou—Xinjiang railway line[J]. Journal of the China Railway Society, 2004, 26(4): 36?40.

[14] Khier W, Breuer M, Durst F. Flow structure around trains under side wind conditions a numerical study[J]. Computers and Fluids, 2000, 29: 179?195.

[15] 田紅旗. 中國列車空氣動力學研究進展[J]. 交通運輸工程學報, 2006, 6(1): 1?9. TIAN Hongqi. Study evolvement of train aerodynamics in China[J]. Journal of Traffic and Transportation Engineering, 2006, 6(1): 1?9.

[16] 嚴雋耄, 傅茂海. 車輛工程[M]. 3版. 北京: 中國鐵道出版社, 2008: 279?287. YAN Juanmao, FU Maohai. Vehicle engineering[M]. 3rd ed. Beijing: China Railway Publishing House, 2008: 279?287.

[17] 王開文.車輪接觸點跡線及輪軌接觸幾何參數的計算[J].西南交通大學學報,1984, 4(1): 89?98. WANG Kaiwen. Trochoid of wheel contact point and calculation on geometry parameters of wheel/rail contact point[J]. Journal of Southwest Jiaotong University, 1984, 4(1): 89?98.

[18] 劉海濤. 強風作用下列車、汽車同時通過公鐵兩用特大橋時的動力響應及行車安全性、舒適性研究[D].長沙:中南大學土木工程學院,2011: 99?100. LIU Haitao. Dynamic responses of train and automobile moving on highway-railway combined bridge under strong wind and analysis of running safety and riding comfort of vehicles[D]. Changsha: Central South University. School of Civil Engineering, 2011: 99?100.

Parametric study on critical speed and overturning stability of high-speed train running on bridge under crosswind

XIANG Chaoqun1, GUO Wenhua1, 2, YAN Junqing1, ZHANG Jiawen1

(1. School of Civil Engineering, Central South University, Changsha 410075, China; 2. National Engineering Laboratory for High Speed Railway Construction, Central South University, Changsha 410075, China)

Based on the theory of computational fluid dynamics, the aerodynamic coefficients of high-speed train running on simply supported box-girder bridge with double lines were computed by numerical simulation, the train's position in marshaling, windward line and leeward line and wind incidence angle were considered, and the results of numerical simulation were compared with those of the wind tunnel test. The formula of accumulated moment to the intersection point of resultant force line of overturning critical situation and the line connecting two side’s wheel-rail contact patch were deduced according to the definition of overturning coefficient of train, the formula involved with train speed and the wind velocity were acquired directly without calculating the wheel/rail interaction force, the computing method for critical speed was gained accordingly, and the parameters affecting the overturning stability of train were analyzed. The results show that the aerodynamic coefficients of train from numerical simulation and wind tunnel test agree well. The head train running on the windward line of the simply supported box-girder bridge with double lines bears the greatest aerodynamic force and its critical speed is the lowest. The critical speed increases with the increase of stiffness coefficient of spring, radius of line, track super elevation and the mass of train, and the critical speed can be overestimated if vertical vibration acceleration is not considered.

aerodynamic coefficient; overturning stability; critical speed; high-speed train; railway bridge with double lines

10.11817/j.issn.1672-7207.2015.05.048

U24

A

1672?7207(2015)05?1929?09

2014?06?22；

2014?08?20

國家自然科學基金資助項目(51078356)；鐵道部科技研究開發計劃重大項目(2008G031-Q) (Project(51078356) supported by the National Natural Science Foundation of China; Project(2008G031-Q)supported by the Major Technology Research and Development Program of Ministry of Railway)

郭文華，教授，博士生導師，從事橋梁結構振動與穩定、風工程研究；E-mail: whguo@126.com

(編輯 陳燦華)