光在金屬界面傳播的實折射角計算

張秋長

(廈門大學嘉庚學院,福建漳州363105)

光在金屬界面傳播的實折射角計算

張秋長

(廈門大學嘉庚學院,福建漳州363105)

通過對光波矢量分別定義等幅面單位矢量和等相面單位矢量,根據光的傳播表達式,分別運用相應的邊界條件,并分別求出了光通過介質/金屬、金屬/介質后的實折射角.通過數值計算可知:對于第1種情況獲得的結果與Born和Wolf通過廣義的斯涅耳折射定律得到的結果一致;金屬/介質的實折射角除了和入射角、介質的折射率、金屬的復光學常數有關外,還與金屬中等幅面單位矢量和等相面單位矢量的夾角有關,且當2個單位矢量之間的夾角滿足一定的關系時,折射角隨著入射角的增大出現先增大后減小的現象.

幾何光學;光折射;Snell定律;復光學常數;光傳輸

早在17世紀上半葉,Snell和Descartes就發現當光線穿越由不同介質構成的界面時會發生折射的現象,并總結出了Snell折射定律,成為現代光學原理的重要基礎[1].這一定律被廣泛應用于理解光在非吸收的透明物質中的傳播行為.但當被擴展和應用于強的光吸收材料,如金屬邊界時,這一問題至今仍未能被很好地認識和理解.

過去的幾十年中許多學者對光散射幾何光學近似(geometrical optics approximation,GOA)進行了研究[2-13],GOA方法能夠克服Mie理論計算大顆粒散射振幅耗時的缺點.而對于吸收性顆粒GOA的研究,存在計算吸收性顆粒中光的傳播路徑和菲涅爾系數的困難[14],有研究者通過引入有效折射率,提出了在吸收性介質中菲涅耳系數的計算公式,也有研究者將吸收顆粒里的非均勻波近似看作均勻波,給出了弱吸收顆粒近似計算的結果,但對于吸收性稍微強的顆粒,以及強的吸收性顆粒,這種近似不再成立[9,15].因為當光折射入吸收性介質時,對應的折射角是一個復數,必須用等效折射角來描述光的實際傳播路徑.本文研究了光在金屬中的傳播以及光在金屬界面的折射規律.分別求出了光通過介質/金屬、金屬/介質邊界時的實折射角.2組實折射角的大小均和入射角、介質的折射率、金屬的復光學常數有關;此外光入射金屬/介質邊界時的實折射角還與金屬中等幅面單位矢量和等相面單位矢量的夾角有關.

1 光在金屬邊界的實折射角問題

Born和Wolf根據麥克斯韋方程和邊界條件,給出了一組計算公式,用于分析和處理光從介質入射到金屬時,已知介質(折射率為na)一側的入射角θa和金屬的光學常數~n=n+iκ,即可計算在金屬一側發生的實折射角[16]:

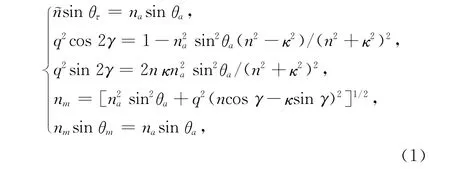
上式中折射角θτ是基于Snell公式的一般意義上在金屬一側的復折射角,nm和θm分別是基于Snell公式的金屬等效實數折射率和光在金屬一側的實折射角,q和δ是計算過程中引入的中間參數.假設光從大氣(na=1)入射金屬銀(~n=0.2+i3.44)[2],按公式(1)計算光在金屬銀一側的實折射角θm隨入射角θa的變化關系,結果如圖1所示.當θa較小時,金屬銀一側的θm與θa近似成線性變化關系,并且由公式(1)可得sin2θa≈0,nm≈n,與金屬折射率的虛部無關.而在大的入射角情況下,θm隨θa的變化趨于平坦.

依據同樣的原理,Garcia-Pomar等給出了光從金屬入射到介質的情況的計算公式,已知金屬銀一側的入射角θm,則在介質一側發生的實折射角θa滿足如下關系[17]:

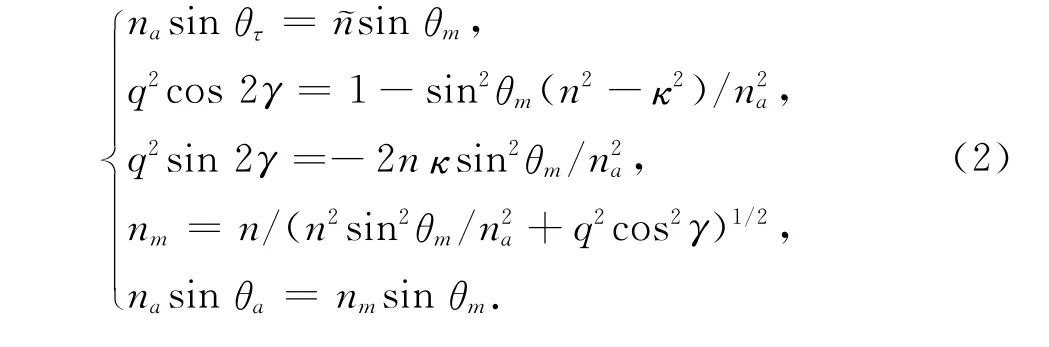
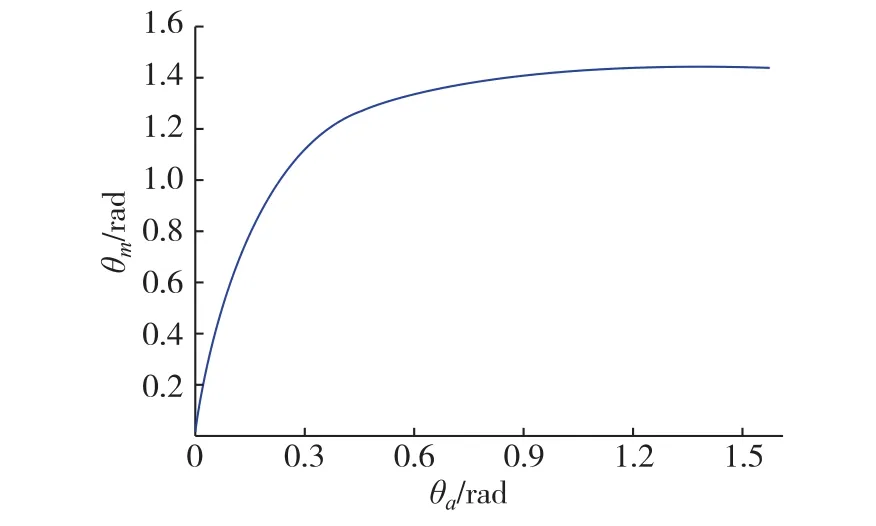
圖1 金屬銀一側的實折射角θm與大氣一側入射角θa的關系Fig.1 Real refractive angleθm at the silver side shows the relationship with the incidence angleθa at the air side

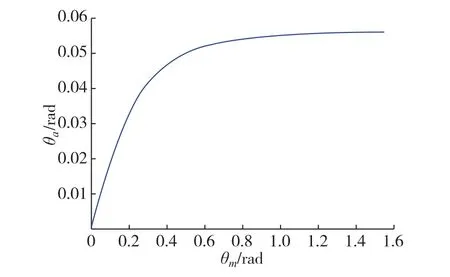
圖2 大氣一側的實折射角θa與銀一側的入射角θm的關系Fig.1 Real refractive angleθa at the air side shows the relationship with the incidence angleθm at the silver side

當光在金屬銀中以入射角θm穿過銀和大氣的界面時,按式(2)計算出光在大氣一側的折射角θa隨入射角θm的變化關系,結果顯示在圖2中.由圖2可知,大氣一側的出射角θa與銀一側的實入射角θm具有圖1中類似的變化關系.若假設光從介質一側入射,穿過平行的金屬銀膜,發生實折射角,又以該折射角作為入射角,從介質一側出射,由于式(1)、(2)中的等效折射率nm具有不同的表達式,可知介質一側的出射角并不等于初始入射角.從圖1中可知,當大氣一側的入射角為0.6 rad時,金屬銀一側的實折射角約等于1.3 rad,而在圖2中,若以1.3 rad作為金屬銀一側的入射角,在大氣一側的折射角約為0.055 rad,約是初始入射角的1/10,這與實驗觀察的結果不一致,即介質一側的出射角應等于初始入射角,所以上述模型具有一定的局限性.雖然2組公式都基于相同的原理,但是由于第2組計算公式入射角是復數角,而處理過程代入計算的是實數角度,忽略了復數角對折射角的影響.所以利用2種模型得到的結果和實驗結果不一致.為了獲得和實驗結果一致的理論模型,本文通過對光波矢量定義等幅面單位矢量和等相面單位矢量,根據光的傳播表達式,分別運用相應的斯涅耳折射定律,求解得到光在金屬界面發生的實折射角,通過分析獲得理論和實驗的統一.

2 光從介質入射到金屬的實折射角

光波在金屬中的傳播如圖3所示,它的等幅面一般不與等相面重合,這樣的波稱為非均勻波,等幅面和等相面的單位矢量分別為q和s,兩單位矢量之間的夾角為ξ=cos-1(q·s).把平面電磁波E(r,t)= E(r)e-iωt,H(r,t)=H(r)e-iωt代人麥克斯韋方程,可以得到光波在金屬中滿足如下方程[16]:

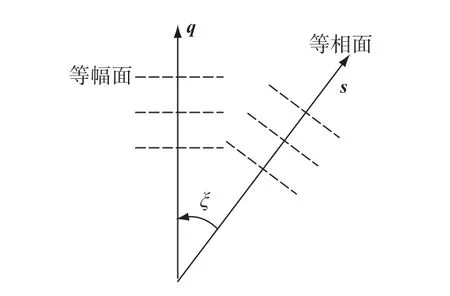
圖3 光在金屬中的傳播Fig.3 Light propagation in metal

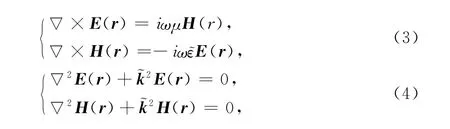
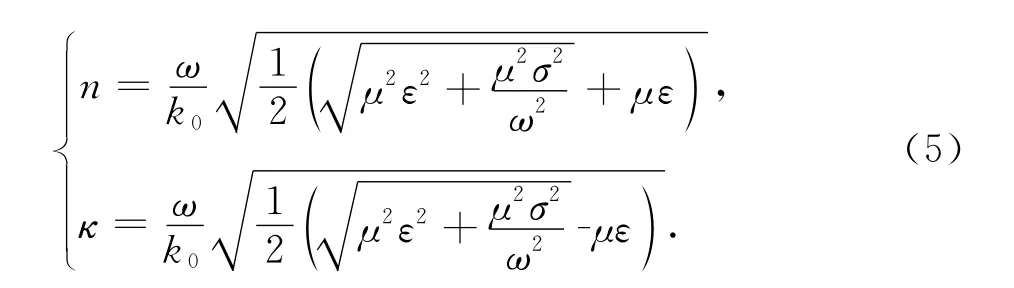
從式(4)可知金屬的復光學常數并不是真正的物質常數,而是隨入射光的頻率改變.雖然根據經典電磁理論,只有厚度異常薄的金屬樣品才能讓入射光有所透過,但在金屬自由電子氣的Drude模型中,當光的頻率足夠大,可預期金屬的光學行為基本上如同介電質,比如有些金屬在長波區不透明并且反射高,而在可見和紫外的某一臨界波長,它們變得透明[16,18].

同時金屬中的光波可表示成:

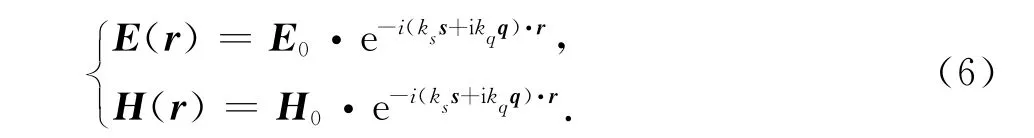
相位常數、衰減常數與光學常數的實部、虛部之間的關系如下:

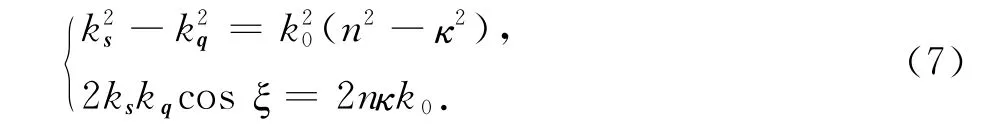
由于n,κ均不為0,從上式可知,ξ≠π/2,即兩單位矢量不會垂直.經計算可得:

設入射波為均勻平面電磁波,Ei(r)=E0i· e-iksi s i·r,其中ksi=nik0(ni為介質的折射率),為簡便起見,考慮入射波在入射面yz平面內,如圖4所示.

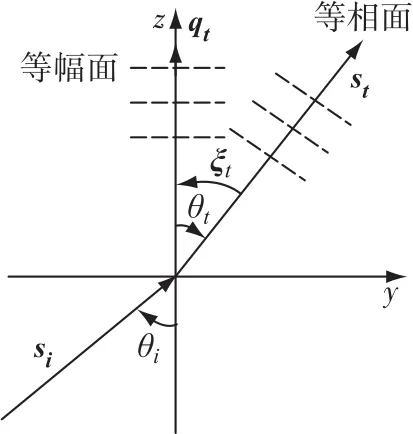
圖4 光在金屬中界面的折射與傳播Fig.4 Light propagation and its refraction at the metal interface

其中入射角為θi,折射角為θt,ξt為z軸和qt的夾角,兩單位矢量之間的夾角ξt=cos-1(qt·st),則根據相位的連續性可知,折射波的等幅面單位矢量和等相面單位矢量也均在入射面yz平面內,由于兩單位矢量不可能垂直,從圖4可知折射角θt肯定小于π/2,并且存在:

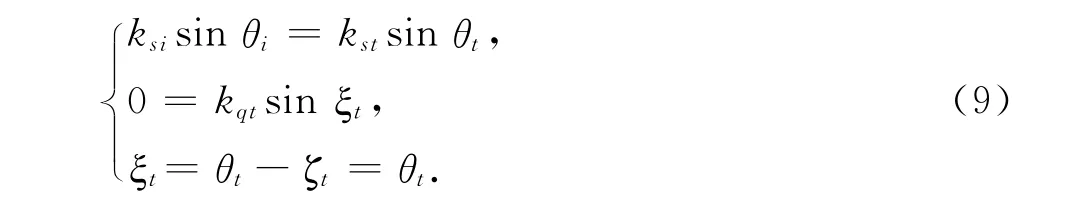
根據式(9)可得折射到金屬的實折射角θt如下:

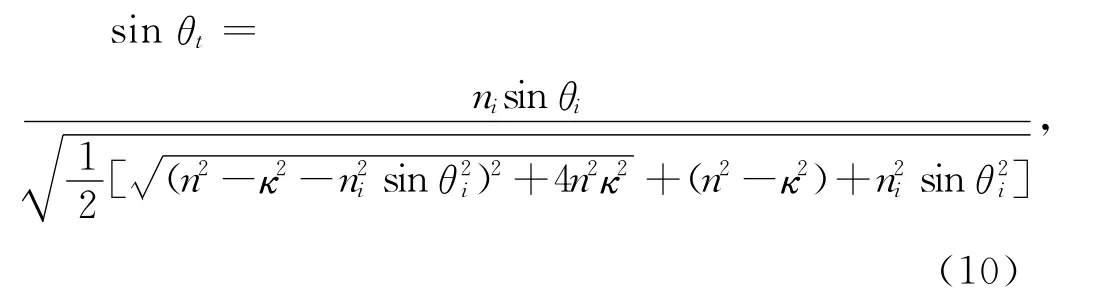
從式(10)可知,折射到金屬的實折射角θt和入射角、介質的折射率、金屬的復光學常數有關.若用等效折射率nm表示式(10)中的平方根,則式(10)可以表示成斯涅耳定律的形式.nm除了取決于表征金屬的物理量,而且還取決于入射角.

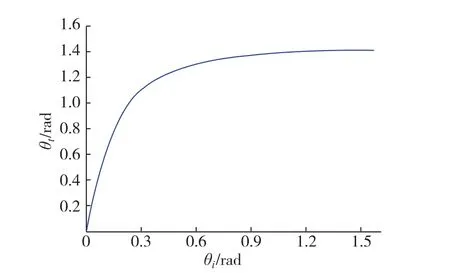
圖5 金屬銀一側的實折射角θt與大氣一側入射角θi的關系Fig.1 Real refractive angleθt at the silver side shows the relationship with the incidence angleθi at the air side

按公式(10)計算光在金屬銀一側的實折射角θt隨大氣一側入射角θi的變化關系,結果如圖5所示.對比圖5和圖1可知兩曲線完全一致,說明新的處理方法與Born和Wolf得到的結果一致.

3 光從金屬入射到介質的實折射角

對于光從金屬入射到介質,考慮折射后的波為E′(r)=E′0·e-i(k′sts′t+ik′qt q′t)·r,考慮入射波在入射面yz平面內(如圖6所示),入射角為θ′i,入射波等幅面單位矢量和法線的夾角為ζ′i,折射角為θ′t,折射波等幅面單位矢量和法線的夾角為ζ′t,折射波兩單位矢量之間的夾角ξt′=cos-1(q′t·s′t),由于金屬中波的相位波矢和衰減波矢在界面上均有切向分量,所以折射波的相位常數k′st,衰減常數k′qt之間的關系如下:

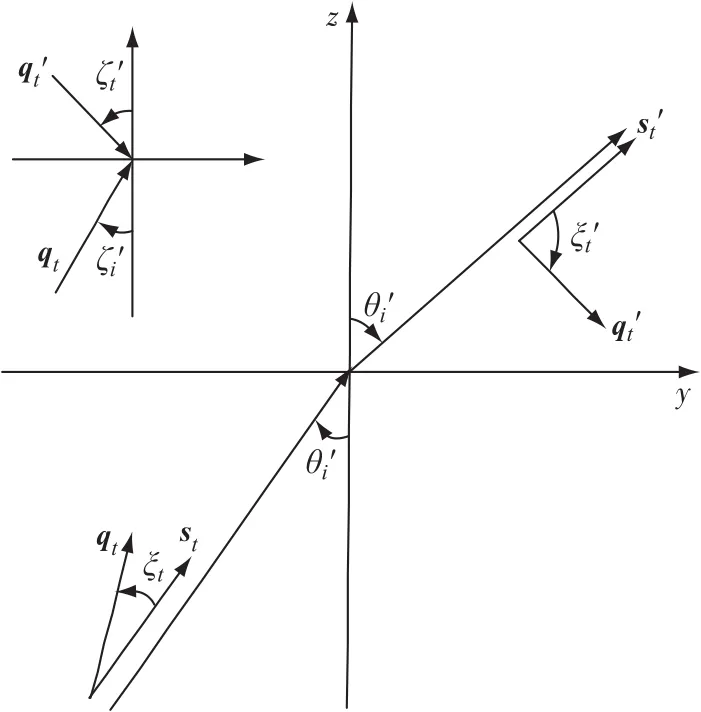
圖6 光從金屬折射到介質Fig.6 Light refraction from metal into medium

從式(11)可知,折射后的波為非均勻平面波,等幅面單位矢量q′t和等相面單位矢量s′t之間的夾角ξ′t=π/2,即兩單位矢量相互垂直.

同理,由邊界條件可知:

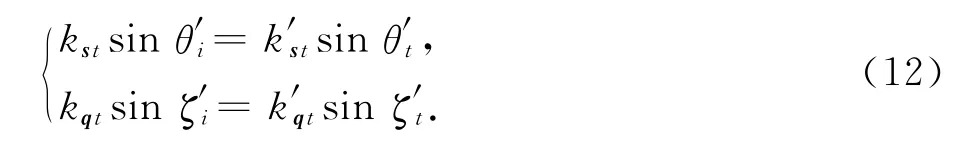
由式(11)、(12)可得折射到介質中的實折射角θ′t由下式決定:

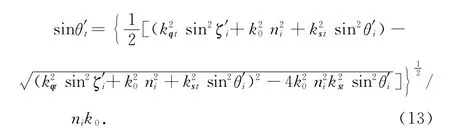
從式(13)可知,如果只給出與式(2)相同的已知條件,則式(13)計算不出實折射角的大小,因為在介質一側的實折射角除了和入射角、介質的折射率、金屬的復光學常數有關外,還與金屬中光波的等幅面單位矢量和等相面單位矢量的夾角有關,這是公式(2)沒有考慮的參數.

假設當光從金屬銀(~n=0.2+i3.44)入射大氣(ni=1)界面時,按公式(13)計算,分別考慮ζ′i=θ′i,ζ′i= θ′i/2,ζ′i=0時折射角θ′t隨入射角θ′i變化關系,從圖7可知對于ζ′i=θ′i,曲線和圖2非常吻合,說明公式(2)只是式(13)的特殊情況,即等幅面和等相面相互平行;而當ζ′i=θ′i/2時,由圖可知折射角θ′t隨入射角θ′i增大出現先增加后減小的現象,若以1 rad作為金屬銀一側的入射角,由圖可得在大氣一側的折射角約分別為0.05 rad、1 rad,由此可知兩單位矢量之間的夾角ξ=cos-1(q·s)的大小對折射角大小的影響很大.所以當光波在金屬中的等幅面與等相面重合(均勻光波),可以使用公式(2)進行計算,而對于更一般的情況還需考慮等幅面單位矢量和等相面單位矢量的夾角對實折射角的影響,此時需要使用式(13)進行計算.

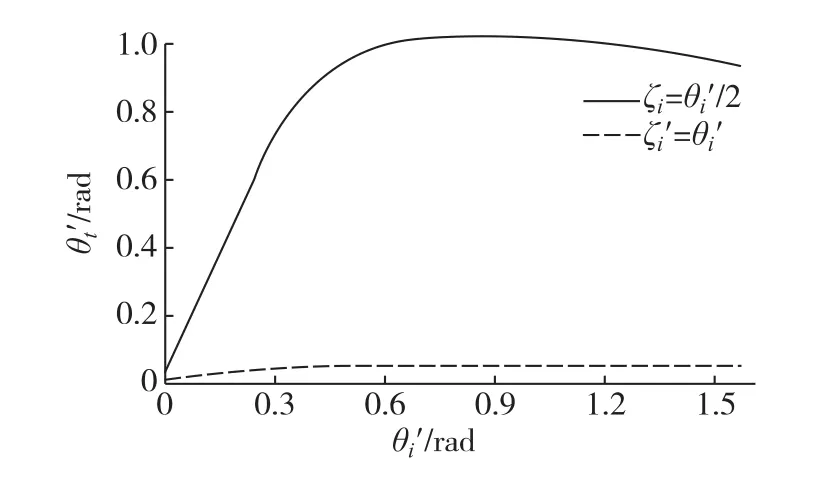
圖7 大氣一側的實折射角θ′t與銀一側的入射角θ′i的關系Fig.7 Real refractive angleθ′t at the air side shows the relationship with the incidence angleθ′i.

當ζ′i=0時,即等幅面單位矢量qt垂直入射界面,此時由于金屬中波的衰減波矢在界面上的切向分量為零,所以折射波的波矢為一實數k′st=nik0,此時折射波為均勻波,相應的邊界條件式(12)變為如下:

若光從介質一側入射,穿過平行的金屬膜,發生折射,從大氣一側出射,綜合式(9)、(14)可知θi等于θ′t,即大氣一側的出射角等于初始入射角.這與實驗觀察到大氣一側的出射角等于初始入射角的結果一致.

4 結 論

本文通過對光波矢量分別定義等幅面單位矢量和等相面單位矢量,研究了光在金屬中的傳播.對兩矢量運用相應的邊界條件,分別求出光通過介質/金屬、金屬/介質邊界時的實折射角.光通過介質/金屬的實折射角與入射角、介質的折射率、金屬的復光學常數有關;而光入射金屬/介質邊界時的實折射角除了和入射角、介質的折射率、金屬的復光學常數有關外,還與金屬中等幅面單位矢量和等相面單位矢量的夾角有關,當兩單位矢量的夾角按一定的規律變化,折射角隨著入射角的增大先增大后減小;均勻光波從介質一側入射,穿過金屬膜,發生實折射角,又以該實折射角作為入射角,從介質一側出射,則介質一側的出射角并不是一個確定的值,還必須給出等幅面單位矢量和等相面單位矢量的夾角才能確定出射角的大小.

[1] Shirley J W.An early experimental determination of Snell′s law[J].American Journal of Physics,1951,19 (9):507-508.

[2] Davis G E.Scattering of light by an air bubble in water [J].Journal of the Optical Soc Am,1955,45(7):572-581.

[3] van de Hulst H C.Light scattering by small particles [M].New Xork:John Wiley&Sons,1957.

[4] Glantschnig W J,Chen S H.Light scattering from water droplets in the geometrical optics approximation[J].Appl Opt,1981,20,2499-2509.

[5] Ungut A,Grehan G,Gouesbet G.Comparisons between geometrical optics and Lorenz-Mie theory[J].Appl Opt, 1981,20:2911-2918.

[6] Hovenac E A.Calculation of far-field scattering from nonspherical particles using a geometrical optics approach [J].Appl Opt,1991(30):4739-4746.

[7] Xu F,Cai X Sh,Ren K F.Geometrical-optics approximation of forward scattering by coated particles[J].Appl Opt,2004,43:1870-1879.

[8] Aden A L,Kerker M.Scattering of electromagnetic waves by two concentric spheres[J].J Appl Phys,1951,22: 1242-1246.

[9] Li X Zh,Han X E,Li R X,et al.Geometrical-optics approximation of forward scattering by gradient-index spheres[J].Applied Optics,2007,46(22):5241-5247.

[10] Xu H T,Shen J Q,Wei X H.Geometrical optics approximation of light scattering by large air bubbles[J].Particuology,2008(6):340-346.

[11] 徐峰,蔡小舒,沈嘉祺.米氏理論的近似及在粒度測量中的應用[J].光學學報,2003,23(12):1464-1469.

[12] 呂且妮,徐暢,靳文華.基于幾何光學近似模型的大氣泡粒子散射光場分布計算[J].天津大學學報:自然科學版,2013,45(12):1089-1095.

[13] 李祥震,韓香娥.利用幾何光學近似計算GI-POF的前向散射[J].紅外與激光工程,2011,40(6):1098-1100.

[14] Xang P,Liou K N.Light scattering by hexagonal ice crystals:comparison of finite-difference time domain and geometric optics models[J].J Opt Soc Am:A,1995,12 (1):162-176.

[15] Xu F,Cai X Sh,Ren K F.Geometrical optics approximation of forward scattering by coated particles[J].Appl Opt 2004,43:1870-1879.

[16] 馬科斯·波恩,埃米爾·沃爾夫.光學原理[M].5版.楊葭蓀,譯.北京:科學出版社,1978.

[17] Garcia-Pomar J L,Nieto-Vesperinas M.Transmission study of prisms and slabs of lossy negative index media [J].Opt Exp,2004,12(10):2081-2095.

[18] Wooten F.Optical properties of solids[M].New Xork: Academic Press,1972.

The Calculation of the Refraction Angle of Light Propagation at Metal Interface

ZHANG Qiu-zhang
(Xiamen University Tan Kah Kee College,Zhangzhou 363105,China)

The light propagation within a metal and the refraction at the interface of metals are studied.On the basis of unit vectors denoting the planes of constant field amplitude and constant phase,respectively,the light propagation and attenuation are described by the complex refractive index of the metal and the angle between the unit vectors,with the expression for the light propagation. Subject to corresponding boundary conditions,refractive angles of the light through the metal/medium and medium/metal interface have been obtained.The numerical analysis shows that resutls for the metal/medium case agree with those the Born and Wolf using snell′s law.The angle of refraction metal/medium depend not only on the incident angle,the refractive index of medium,and the complex refractive index of metal,but also on the angle between the planes of constant amplitude and of constant phase.While the angle between the two unit vectors satisfies a certain relation,the angle of refraction increases first and then decreases with the increase of incident angle.

geometric optics;light refraction;Snell law;complex optical constants;light propagation

10.6043/j.issn.0438-0479.2015.02.016

O 435

A

0438-0479(2015)02-0242-05

2014-02-20 錄用日期:2014-05-29

Email:zqzhang@xujc.com

張秋長.光在金屬界面傳播的實折射角計算[J].廈門大學學報:自然科學版,2015,54(2):242-246.

:Zhang Qiuzhang.The calculation of the refraction angle of light propagation at metal interface[J].Journal of Xiamen U-niversity:Natural Science,2015,54(2):242-246.(in Chinese)