車橋豎向隨機振動的概率密度演化分析

余志武，毛建鋒，談遂，曾志平

?

車橋豎向隨機振動的概率密度演化分析

余志武，毛建鋒，談遂，曾志平

(中南大學土木工程學院，高速鐵路建造技術國家工程實驗室，湖南長沙，410075)

基于車?橋豎向耦合模型，引入不平順功率譜隨機諧和函數，采用維超立方體點集(gp集)選取離散隨機頻率代表點，得到代表性軌道高低不平順隨機激勵樣本并進行慢變調制；建立概率密度演化方法的隨機動力方程，基于MATLAB編制車橋耦合隨機振動概率密度演化分析程序；采用newmark-積分法及帶TVD格式的雙邊差分法計算車橋振動響應的均值、標準差及時變概率密度演化分布。研究結果表明：與Monte Carlo法相比，概率密度演化法分析車橋隨機振動精度更高，計算效率提高1~2個數量級；輸入均勻隨機分布頻率和初相位的軌道不平順激勵，輸出響應并非均勻分布，隨車速先增加后減少，概率分布呈高斯型分布；軌道不平順引起的系統隨機響應受車速影響較大。

車橋耦合模型；概率密度演化方法；軌道高低不平順；維超立方體點集；功率譜

車橋系統是一個復雜時變的隨機系統，結構參數、輸入激勵及輸出響應等均具有極強的隨機性。國內外學者針對高速鐵路車橋耦合振動領域，對模型建立及輪軌激勵下的系統響應進行了研究[1?4]。利用1條或幾條實測或模擬的軌道不平順激勵樣本產生的系統響應具有很大的離散性[5]，對于由隨機激勵作用造成的系統影響及程度，現有的方法尚不能全面地考慮系統的隨機振動響應特性，而經典的Monte Carlo法因計算量巨大而研究較少。在工程實踐中，人們不但關心結構響應標準差等統計量，而且重視對結構響應均值及最大值等的控制，僅進行少數確定性時程分析，這遠遠不夠，因此，迫切需要深入發展車橋耦合隨機振動研究。目前，車橋隨機振動分析方法主要有隨機模擬法、隨機攝動法、概率密度演化方法[6?7]及虛擬激勵 法[8?9]等。李杰、陳建兵等[6]建立的廣義概率密度演化方程，在線性與非線性多自由度結構系統隨機反應分析、可靠度計算等方面取得了較系統的成果。該法可輸出高精度系統響應均值、標準差及概率密度演化過程。陳建兵等[10]還提出了基于功率譜的隨機諧和函數表達，使結構的隨機振動理論趨于完善。軌道不平順激勵具有明顯的時變隨機性，用概率密度隨機理論來描述軌道不平順的隨機性是合理并具有較高計算精度。本文作者針對軌道高低不平順激勵的隨機性，結合廣義概率密度演化方法[11]，據車橋耦合系統隨機振動的客觀實際狀態實現車橋系統的隨機振動響應分析，以便得到系統振動的時變響應全概率演化信息。

1 代表性軌道不平順樣本激勵

1.1 軌道隨機不平順隨機模擬

在空間域中，軌道不平順為一系列以為橫坐標的軌道空間位置，除了得到實測值外還可進行數值模擬。軌道不平順功率譜模型與地震功率譜不同，其在截止頻率范圍內譜值呈指數變化[12]。無論隨機頻率如何，具有隨機頻率和相位的隨機諧和函數過程的功率譜精確等于原功率譜[13]，因此，頻率截斷的級數越多，便可得到輸出響應的概率信息越精確。

根據文獻[13]，豎向軌道不平順激勵可模擬為隨機諧和函數：

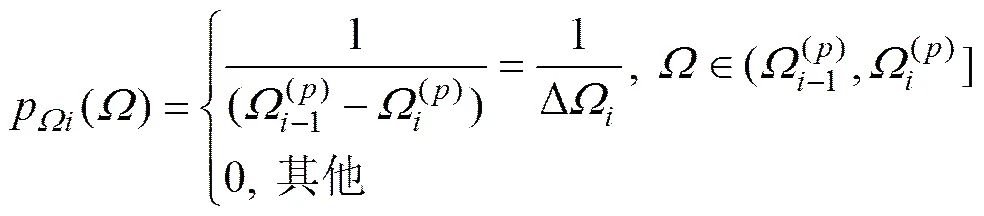
則由式(1)表達的隨機過程y()的功率譜函數為。因而，功率譜密度函數滿足[10, 14]

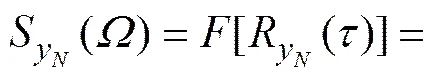
1.2 gp集選取離散代表點

軌道高低不平順隨機諧和函數y()中，隨機向量維數為2，不平順空間頻率離散點的選取直接影響計算的精度。為得到隨機函數全概率信息的代表性樣本，可先討論2維隨機向量的選點問題。據方開泰等[14]的研究，由平方根序列法生成2維超立方體點集(gp集)：

可認為式(4)是2維超立方體中的均勻散布點集，其中為互不相同的素數，表示小數部分。文獻[15]建議在一般情況下，依次取前個素數，空間頻率與角頻率的關系為，為軌道不平順波長，為列車運行速度，則由下式變換得到離散代表點：

其中：=1，2，…，；=1，2，…，n。每一組點集的初始賦值概率均為，n為代表點集總組數。根據gp集合的偏差[14]，，=1，2，…；為構成的點集。將式(5)代入式(1)，則可得代表性軌道高低不平順激勵函數：

1.3 軌道不平順激勵的空間域與時域轉換及慢變 調制

橋面上的軌道平順性比一般路基地段的高[2]，因此，需要對橋上軌道不平順進行調制。假設軌道不平順為空間域內的均勻調制演變非平穩隨機過程(其中，為正弦慢變調制函數，y()為以空間坐標為自變量的零均值平穩隨機過程)。通過關系式可將軌道不平順激勵由空間域轉換為時間域，即

2 車橋豎向振動概率密度演化方程的建立及求解

2.1 輪軌關系假設

假設：1) 車輛始終以速度勻速運行；2) 車體、輪對與鋼軌均視為剛體；3) 輪對不脫離鋼軌，車輪在鋼軌上運行時不發生滑動，無爬軌、跳軌和脫軌現象發生。

根據假定，考慮豎向軌道不平順激勵的隨機性，輪軌幾何關系表述為

2.2 車橋豎向隨機動力方程

由輪軌關系假設可知，輪軌不具有彼此獨立的自由度，車輛系統具有6個獨立自由度，記為。由彈性系統動力學總勢能不變值原理[3]及形成矩陣的“對號入座”法則即可得系統有限元振動方程。車輛系統動力方程為

其中：

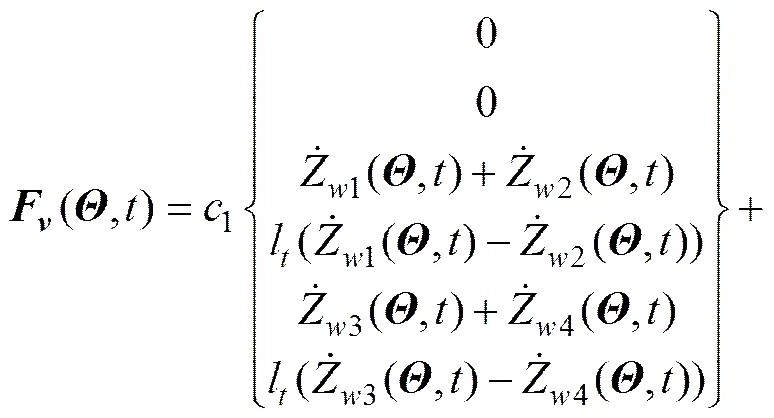
橋梁結構假設為Bernoulli?Euler簡支梁，對橋梁進行有限元離散得到動力方程：

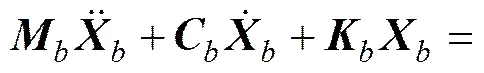
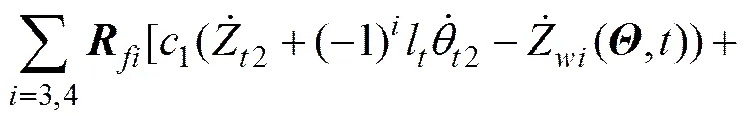
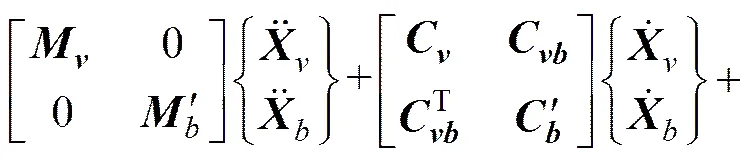
車橋動力系統是復雜耦合的動力系統，系統方程具有很強的時變性和隨機性。由于車橋時變系統中非線性因素難以把握及求解困難等，在一般情況下，動力方程(11)描述為適定的動力學系統，暫不考慮非線性因素。在給定的初始條件作用時，車橋耦合隨機振動方程依賴于隨機變量，其解答存在且唯一。

2.3 隨機振動的概率密度演化求解

假定車橋系統只有軌道高低不平順隨機激勵源，中間沒有新的隨機源產生，則此系統滿足概率守恒條件[15]。

1) 由式(1)及式(4)提供的gp集獲得軌道高低不平順樣本，并經式(7)對隨機不平順樣本進行調制非平穩化及頻域與時域的轉換，從而得到非平穩的軌道不平順樣本，并確定各軌道高低不平順代表樣本的初始賦得概率P。

2) 基于式(11)建立的隨機激勵車橋動力方程，利用newmark-高效逐步積分法，求解給定隨機變量的代表性樣本激勵作用下的隨機振動方程(11)，輸出系統響應，和。

在車橋耦合動力分析中，位移、速度和加速度等是衡量行車安全和穩定的重要因素。對于一般性結構而言，結構響應均可其位移和速度響應確定[16]。據此，可設為待求解系統隨機向量(其中，為需求解響應數量)，則有，將式(12)代入得

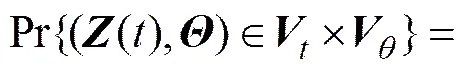
或

式中：Pr為概率函數；為時刻變量的時域分布，為隨機變量的響應分布，D/D為對概率密度函數的全導數。

根據Reynold轉換定理和相關推導，并將式(14)代入式(15)和(16)，可得廣義密度演化方程[12]：

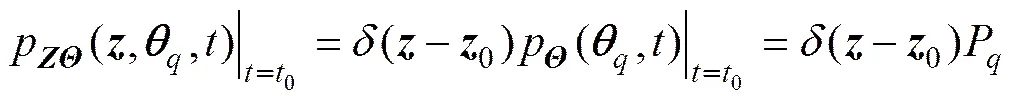
確定初始條件式(18)后，利用帶TVD格式的雙邊差分法[6]求解偏微分方程(18)，獲得的解答，即可得系統響應的概率密度函數：

3 算例分析及驗證

本文以32 m標準簡支箱梁、德國ICE動車組為工程背景，建立三跨簡支梁豎向車橋耦合動力方程，在MATLAB計算平臺上編制基于概率密度演化方法的車橋豎向耦合振動程序，以軌道高低隨機不平順作為輸入激勵。為方便與Monte Carlo法進行比較，采用4列車編組即動+拖+拖+動，運行時速為60~400 km/h；采用德國低干擾軌道高低不平順譜，空間頻率Ω[0.05，3] rad/m，隨機頻率數=30，高低不平順代表性樣本組數n=300；箱梁基本參數為：=3.45×104N/mm2，=8.89 m2，I=10.95 m4，其一階、二階自振頻率分別為5.12 Hz和17.04 Hz；橋上不平順調制系數=0.65，調制過渡段長度0=20 m，列車從距離橋頭?150 m處開始運行，保證列車振動穩定后再上橋。

3.1 計算效率與精度的驗證

圖1~3所示為軌道高地不平順隨機激勵作用下的豎向車橋時變耦合系統概率密度演化分析結果，包括三維概率密度演化圖、等概率密度曲線圖、均值及標準差曲線圖。為驗證本文方法的高精確性，分別與經典Monte Carlo 隨機分析方法各計算結果進行對比。分析對比圖1~3所示響應，Monte Carlo法200次、1 000次和5 000次的運行結果與概率密度演化?newmark逐步積分法(PDF-NEWMARK)300組代表時程計算結果的最大偏差如下：橋梁跨中撓度標準差分別為18.62%，7.55%和2.02%；第1節列車豎向位移標準差分別為19.87%，4.58%和1.75%；第1節列車豎向加速度標準差分別為15.47%，5.42%和1.23%。研究表明，采用PDF-NEWMARK 300組代表性樣本分析時即可達到Monte Carlo 法5 000次計算相當的精度，而300組PDF需時95.1 min，而5 000次Monte Carlo法耗時1 623 min，可見與Monte Carlo法相比，計算效率提高了1~2個數量級。因此，概率密度演化方法具有較高的精度與計算效率，驗證了文獻[6]中的結論。

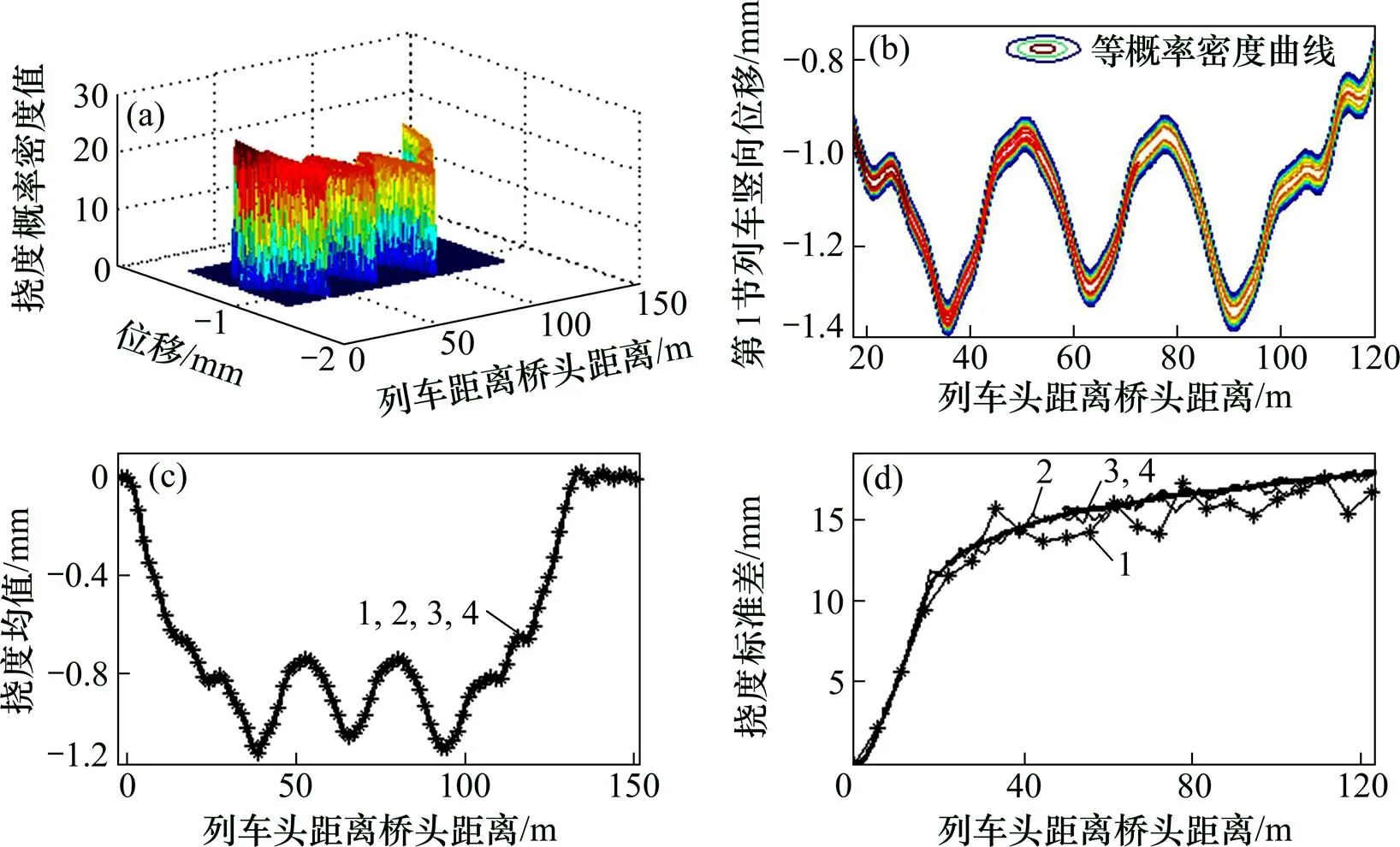
(a) 撓度PDF；(b) 等概率密度曲線；(c) 撓度均值；(d) 撓度標準差1—Monte Carlo 200；2—Monte Carlo 1 000；3—Monte Carlo 5 000；4—PDF-NEWMARK 300

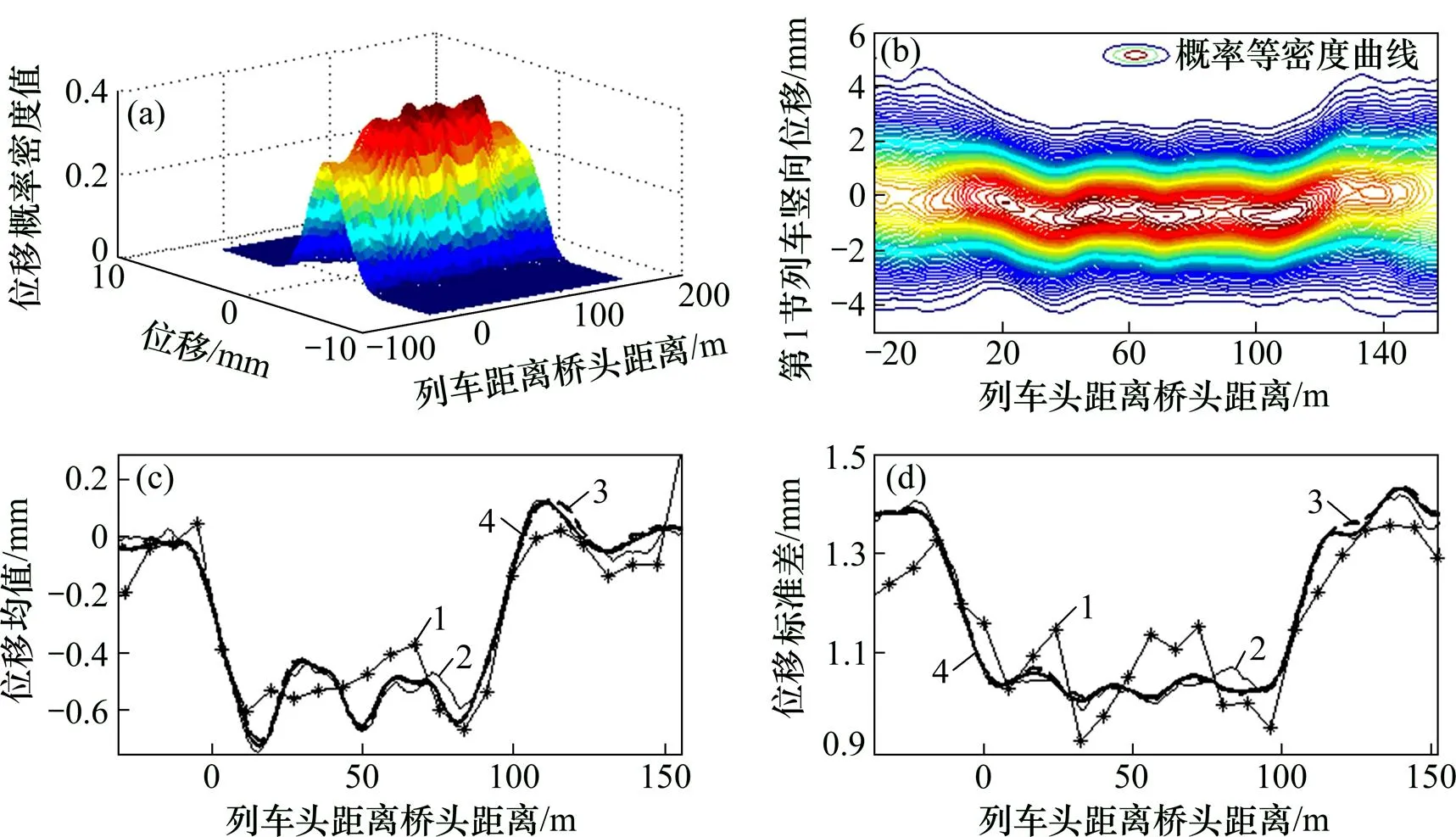
(a) 位移PDF；(b) 等概率密度曲線；(c) 位移均值；(d) 位移標準差1—Monte Carlo 200；2—Monte Carlo 1 000；3—Monte Carlo 5 000；4—PDF-NEWMARK 300

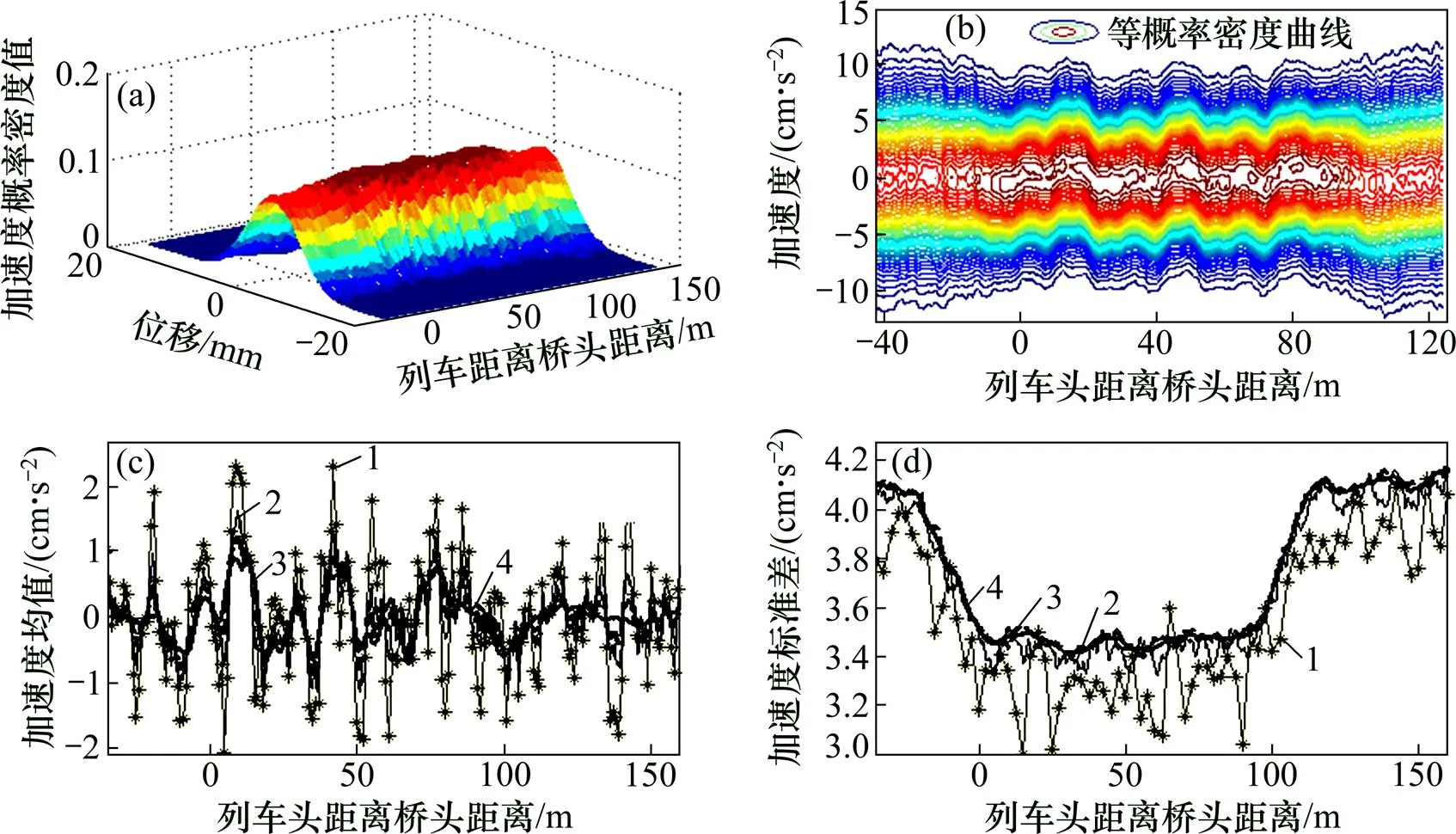
(a) 加速度PDF；(b) 等概率密度曲線；(c) 加速度均值；(d) 加速度標準差

分析圖1可知：120 km/h速度下第1跨梁跨中豎向撓度均值最大值為1.13 mm，相應標準差最大值為0.02 mm，變異系數為1.79%，軌道不平順對橋梁動力響應較小，其等概率密度演化曲線分布范圍相對狹窄，概率密度峰值符合響應均值趨勢分布。

對圖2所示的對等概率密度演化曲線、均值及標準差曲線進行分析可知：120 km/h速度下第1節列車重心豎向位移響應均值最大值為?0.73 mm，相應標準差為1.04 mm，變異系數為143.0%。對比圖1與圖2可知：軌道高低不平順激勵對車體豎向位移響應的影響遠大于橋梁撓度響應的影響。列車豎向位移均值在通過三跨橋梁時，存在隨橋梁撓度變化一致的耦合響應規律及在出橋時刻的動力增大效應，這一現象對于單一或少數軌道不平順樣本激勵作用下的響應曲線是難以發現的，這亦驗證了概率密度演化法能精確模擬列車與橋梁的動力耦合作用。標準差數值變化符合橋上軌道不平順慢變調制規律，上橋后的標準差與未上橋時的比例接近0.65。

分析圖3可知：120 km/h速度下第1節列車重心豎向加速度響應均值最大值為0.90 cm/s2，相應標準差為3.88 cm/s2，變異系數達431.0%，列車振動加速度受軌道不平順影響很大；列車過橋時加速度變化范圍亦受橋梁撓度及調制函數的影響，加速度均值基本在零均值附近擺動，在三跨橋位置均明顯增大，之后趨于平緩；加速度標準差隨調制函數的變化趨勢顯著，加速度概率密度曲線與實際曲線相吻合。

3.2 振動響應及車速影響分析

隨著列車車速的增加，車橋耦合振動呈現不同的響應規律，因此，將車速分為13個等級，每30 km/h為1個工況，從60 km/h到420 km/h等間距分布。圖4~7所示分別為不同車速等級下，列車通過橋梁出現最大均值響應時的第1跨橋梁跨中豎向撓度、第1節列車重心位移及加速度均值、標準差及概率分布。圖5~7中：和分別為均值和標準差；±，±2和±3分別代表1倍標準差上下界、2倍標準差上下界、3倍標準差上下界。

v/(km·h?1)：1—60；2—120；3—180；4—240；5—300；6—360；7—390

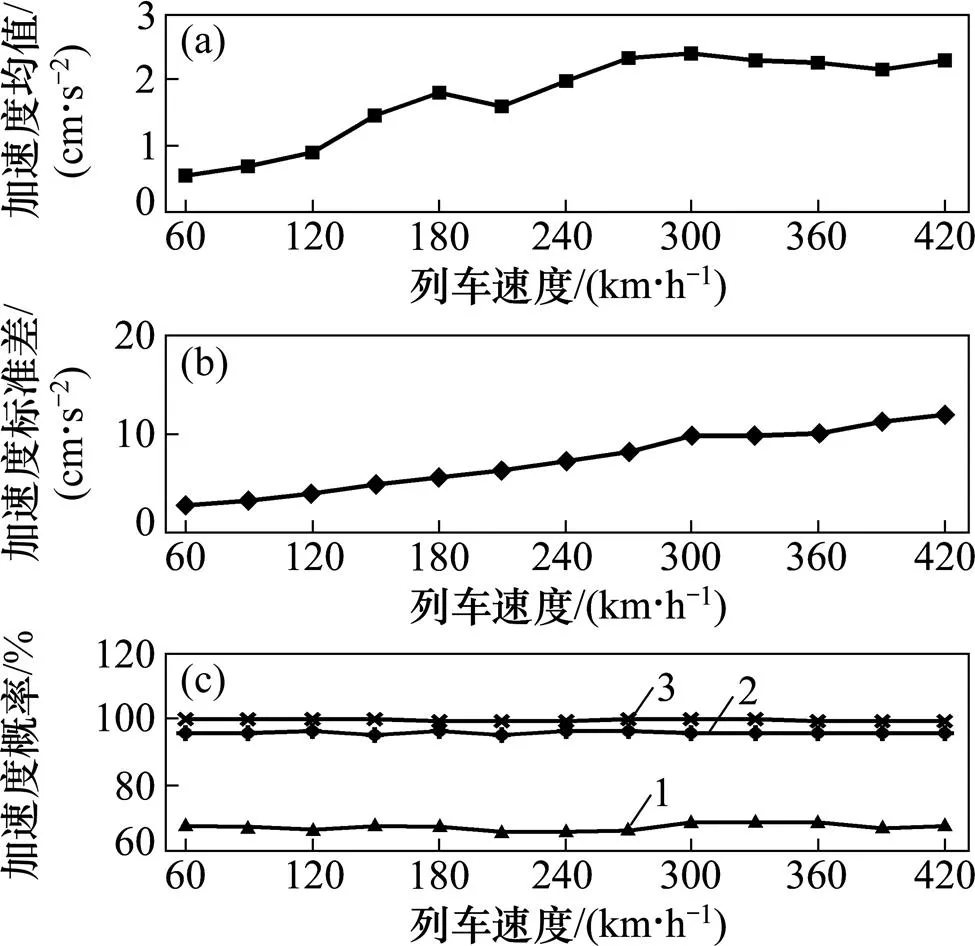
(a) 加速度均值；(b) 加速度標準差；(c) 加速度概率1—μ±σ；2—μ±2σ；3—μ±3σ

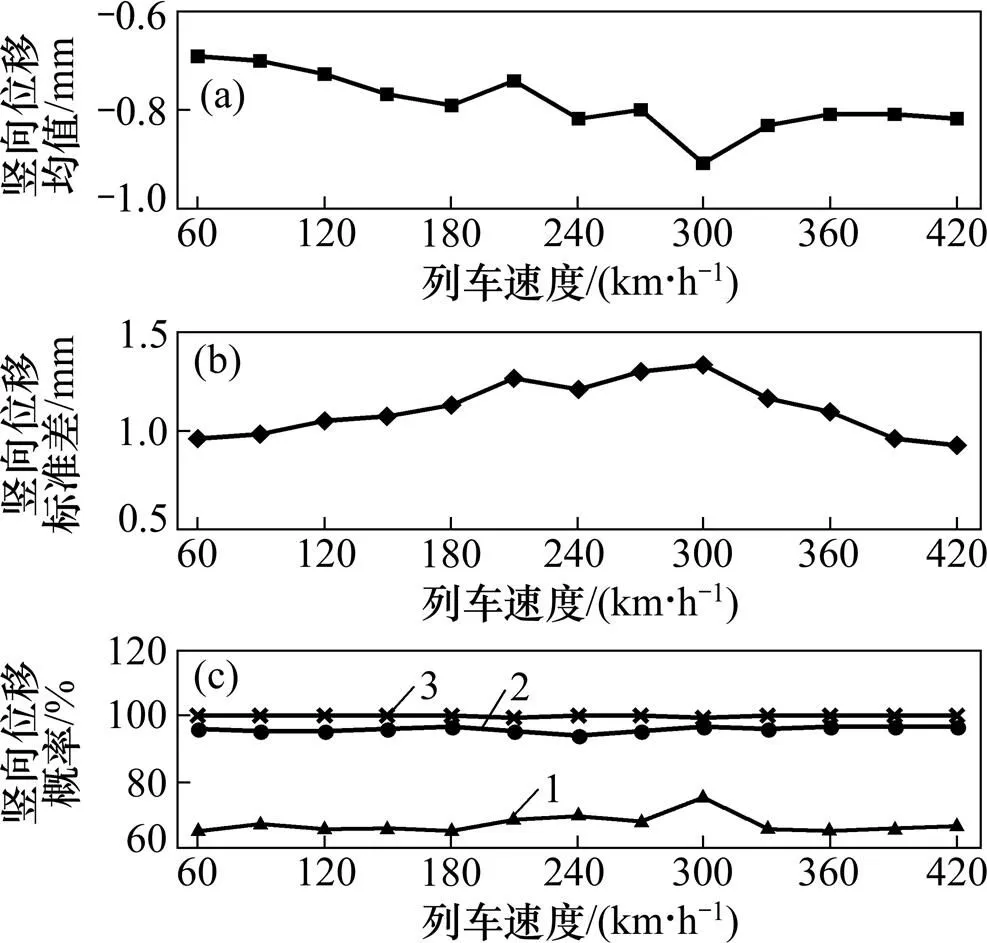
(a) 豎向位移均值；(b) 豎向位移標準差；(c) 豎向位移概率1—μ±σ；2—μ±2σ；3—μ±3σ

(a) 撓度均值；(b) 撓度標準差；(c) 撓度概率1—μ±σ；2—μ±2σ；3—μ±3σ

圖4所示為不同速度等級下列車通過第1跨橋梁跨中時列車豎向加速度響應分布的概率密度曲線，為清晰顯示，圖中只給出了間隔60 km/h時速的概率密度演化曲線，每一概率演化曲線閉合面積為概率值1。從圖4可見：隨著車速增加，概率密度曲線主體重心逐漸右移，概率密度曲線峰值逐漸減小而相應的加速度響應分布范圍逐漸增大，這也符合圖5中列車加速度響應均值和標準差的分布規律。

從圖5~7中的均值和標準差分布可知：隨著車速增加，車橋耦合振動響應均不同程度增大，橋梁跨中撓度值均和標準差、列車豎向加速度均值和標準差及列車豎向位移的均值和標準差均在300 km/h附近出現響應峰值。這是由于32 m標準跨橋梁一階自振頻率5.12 Hz與列車在時速300 km/h下通過橋梁時發生的強振頻率較接近，系統發生共振耦合而形成的。對比圖5~7可知：在±響應范圍內，概率保證度保持在(65±5)%；在范圍內，概率保證度達95%以上；在±范圍內，概率保證度基本可以達到99.5%以上，基本符合高斯型正態分布。

4 結論

1) 概率密度演化法能精確分析車橋耦合隨機振動，與Monte Carlo法相比，驗證了概率密度演化法的高效性和高精度性，計算效率提高1~2個數量級。

2) 輸入具有均勻隨機分布的頻率和初相位的軌道不平順激勵，對應輸出的系統響應并非均勻分布，而是呈現高斯正態分布規律。

3) 軌道高低隨機不平順激勵對列車豎向振動影響遠大于橋梁振動的影響，在一定時速范圍內兩者振動響應均值、標準差隨車速增加而增大。

4) 振動響應概率分布范圍隨車速的增加逐漸平緩擴大，概率特性基本符合高斯型分布。

5) 列車與橋梁具有較強的耦合作用，并受橋上軌道不平順慢變調制函數影響明顯。

[1] ZHANG Nan, XIA He, GUO Weiwei. Vehicle-bridge interaction analysis under high-speed trains[J]. Journal of Sound and Vibration, 2008, 309(3/4/5): 407?425.

[2] 夏禾, 張楠. 車輛與結構動力相互作用[M]. 2版. 北京: 科學出版社, 2005: 321?359. XIA He, ZHANG Nan. Dynamic interaction of vehicles and structure[M]. 2nd ed. Beijing: Science Press, 2005: 321?359.

[3] 曾慶元, 郭向榮. 列車橋梁時變系統振動分析理論與應用[M]. 北京: 中國鐵道出版社, 1999: 49?88. ZENG Qingyuan, GUO Xiangrong. Theory and application of train-bridge time-variant system vibration analysis[M]. Beijing: China Railway Press, 1999: 49?88.

[4] 翟婉明. 車輛一軌道耦合動力學[M]. 3版. 北京: 科學出版社, 2007: 12?84. ZHAI Wanming. Vehicle?track coupling dynamics[M]. 3rd ed. Beijing: Science Press, 2005: 12?84.

[5] 王貴春, 潘家英. 軌道不平順導致的車橋耦合振動分析[J]. 鐵道工程學報, 2006, 96(8): 30?33. WANG Guichun, PAN Jiaying. Analysis of vehicle- bridge coupled vibration due to track irregularities[J]. Journal of Railway Engineering Society, 2006, 96(8): 30?33.

[6] 李杰, 陳建兵. 隨機動力系統中的概率密度演化方程及其研究進展[J]. 力學進展, 2010, 40(2): 170?188. LI Jie, CHEN Jianbing. Advances in the research on probability density evolution equations of stochastic dynamical systems[J]. Advances in Mechanics, 2010, 40(2): 170?188.

[7] LI Jie, CHEN Jianbing. Probability density evolution equations: A historical investigation[J]. Journal of Earthquake and Tsunami, 2009, 3(3): 209?226.

[8] ZHANG Zhichao, LIN Jiahao, ZHANG Yahui, et al. Non-stationary random vibration analysis for train bridge systems subjected to horizontal earthquakes[J]. Engineering Structures, 2010, 32(11): 3571?3582.

[9] 林家浩, 張亞輝. 隨機振動的虛擬激勵法[M]. 北京: 科學出版社, 2006: 60?76.LIN Jiahao, ZHANG Yahui. Random vibration of the pseudo-excitation method[M]. Beijing: Science Press, 2006: 60?76.

[10] 陳建兵, 李杰. 隨機過程的隨機諧和函數表達[J]. 力學學報, 2011, 43(3): 505?513. CHEN Jianbing, LI Jie. The stochastic process of random harmonic functions[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(3): 505?513.

[11] LI Jie, CHEN Jianbing. The principle of preservation of probability and the generalized density evolution equation[J]. Structural Safety, 2008, 30(1): 65?77.

[12] 陳憲麥.軌道不平順時頻域分析及預測方法的研究[D]. 北京: 鐵道部科學研究院, 2006: 5?14. CHEN Xianmai. Time-frequence analysis and prediction study on track irregularities[D]. Beijing: Ministry of Railways Science Institute, 2006: 5?14.

[13] 孫偉玲, 陳建兵, 李杰. 隨機過程的第二類隨機諧和函數表達[J]. 同濟大學學報(自然科學版), 2011, 39(10): 1413?1419.SUN Weiling, CHEN Jianbing, LI Jie. Stochastic harmonic functions of second kind for spectral representations[J]. Journal of Tongji University (Natural Science), 2011, 39(10): 1413?1419.

[14] 方開泰, 王元. 數論方法在統計中的應用[M]. 北京: 科學出版社, 1995: 24?30.FANG Kaitai, WANG Yuan. Number-theoretic method in statistics chapman and hall[M]. Beijing: Science Press, 1995: 24?30.

[15] LI Jie, CHEN Jianbing, SUN Weiling, et al. Advances of the probability density evolution method for nonlinear stochastic systems[J]. Probabilistic Engineering Mechanics, 2012, 28(SI): 132?142.

[16] FUNG Yuancheng. A first course in continuum mechanics[J]. Prentice-Hall Inc, 1994.

(編輯 陳燦華)

Probability density evolution analysis of track-bridge vertical coupled vibration with irregularity random excitation

YU Zhiwu, MAO Jianfeng, TAN Sui, ZENG Zhiping

(National Engineering Laboratory for High Speed Railway Construction, School of Civil Engineering, Central South University, Changsha 410075, China)

Based on the simple vertical model of the train-bridge system, the random harmonic functions of track vertical irregularity power spectrum were introduced. The representativepoints of random frequency were selected by utilizing the-dimensional hypercube point set method, which formed the sample of random excitation modulated by the slowly varying function. The random dynamicequation for probability density evolution method was formulated, and by using MATLAB, program for the probability density evolution and analysis of train-bridge coupled random vibration were developed. Eventually, newmarkintegration method and double edge difference method of TVD format were adopted to obtain the mean value, the standarddeviation and the distribution of the time dependent probability density evolution. The results show that compared to the Monte Carlo method, the probability density evolution method has higher accuracy and computation efficiency, with efficiency improved by 1?2 order of magnitudes. When the excitation with randomly distributed frequency and initial phrase for track vertical irregularity is input, the output is not uniformly distributed, rather it distributes in Gaussian style, i.e., with the increase of train speed, the response of system firstly increases and then decreases. The random system response incurred by track vertical irregularity is significantly influenced by trains speed.

train-bridge system model; probability density evolution method; vertical track irregularity;-dimensional hypercube point set; power spectrum

10.11817/j.issn.1672-7207.2015.04.032

U24

A

1672?7207(2015)04?1420?08

2014?04?12；

2014?06?23

國家自然科學基金資助項目(51278496，51378513)；長江學者創新團隊發展計劃資助項目(IRT1296)；鐵道部科技開發計劃項目(2013G003-A-3)(Projects (51278496, 51378513) supported by the National Natural Science Foundation of China; Project (IRT1296) supported by the Program for Changjiang Scholars and Innovative Research Team in University; Project (2013G003-A-3) supported by Ministry of Railway Technology Development Projects)

毛建鋒，博士研究生，從事車橋耦合隨機振動研究；E-email：csumjf@csu.edu.cn