基于宏觀和細觀缺陷耦合的節理巖體損傷本構模型

趙怡晴，劉紅巖，呂淑然，張力民,6

?

基于宏觀和細觀缺陷耦合的節理巖體損傷本構模型

趙怡晴1，劉紅巖2,3,4，呂淑然5，張力民1,6

(1. 北京科技大學土木與環境工程學院，北京，100083；2. 中國地質大學(北京) 工程技術學院，北京，100083；3. 西藏大學工學院，西藏拉薩，850000；4. 中國地質大學(北京) 國土資源部深部地質鉆探技術重點實驗室，北京，100083；5. 首都經濟貿易大學安全與環境工程學院，北京，100026；6. 河北承德鋼鐵公司，河北承德，067000)

提出考慮宏觀和細觀缺陷耦合的節理巖體損傷本構模型。首先介紹僅考慮微裂紋等細觀缺陷影響的巖石損傷本構模型及僅考慮節理等宏觀缺陷影響的巖體損傷本構模型，其次基于Lemaitre應變等效假設，推導考慮宏觀和細觀缺陷耦合的復合損傷變量，從而建立基于宏觀和細觀缺陷耦合的節理巖體損傷本構模型，最后通過引用巖石單軸壓縮試驗資料對模型合理性進行驗證。研究結果表明：該模型能夠較好地同時反映宏觀和細觀缺陷對巖體應力應變曲線的影響。同時采用該模型對含不同傾角的單節理巖體和含多條平行節理的巖體在單軸壓縮荷載下的應力應變曲線進行分析，所得結果與相關文獻中的試驗及理論結果具有很好的一致性，說明了該模型的合理性。

節理巖體；損傷本構模型；宏觀缺陷；細觀缺陷；損傷耦合

通常認為巖體是由結構體(巖石)和結構面(節理、裂隙等)所組成，而宏觀上相對完整的巖石則含有眾多的微裂紋、微孔洞等細觀缺陷。因此巖體內的損傷缺陷包含具有從宏觀到細觀甚至微觀的各種尺度，節理、裂隙是其宏觀損傷的表現，而空洞、孔隙、顆粒界面和微細觀裂紋則是其細觀損傷的表現。各種不同尺度的損傷缺陷分別從不同側面以不同的作用機理對巖體物理力學性質產生影響，如很多學者[1?3]分別采用理論、試驗及數值方法證明了節理、裂隙等宏觀缺陷的存在將導致巖體力學性質產生明顯的各向異性，另一方面在巖體內部隨機分布的微裂隙等細觀缺陷的存在將導致其產生各向同性損傷，使巖體強度降低、剛度弱化[4?6]。然而宏觀損傷和細觀損傷并不是孤立存在的，而是相互聯系的。宏觀損傷是由大量的細觀損傷裂紋經過起裂、擴展、分叉等復雜的損傷演化過程而產生。但是目前關于巖體損傷力學的研究都是將上述兩種不同尺度的缺陷割裂開來，單獨研究其對巖體力學性質的影響。如Kawamoto等[7]均只考慮節理等宏觀缺陷對巖體力學性質的影響，采用二階損傷張量反映其對巖體造成的各向異性特征，而不考慮被節理切割而成的巖塊內部存在的微裂隙等細觀缺陷的影響。同樣Grady等[8]則僅考慮微裂紋等細觀損傷對巖石力學性質的影響，以微裂紋密度作為參量定義損傷變量，而不考慮微裂紋擴展、聚合后形成宏觀裂紋進而導致巖體各向異性的情況。因此上述2種方法都沒有同時反映2種不同尺度缺陷對巖體力學性質的影響。而相關試驗表明[9]巖體內同時存在的宏觀和細觀損傷均對巖體的力學性質產生影響，而且這2種不同尺度的缺陷之間還可能存在著復雜的相互作用。因此，如何更好地同時反映2種不同尺度缺陷對巖體力學性質的影響是目前巖體損傷力學研究中一個亟待解決的重要課題。由目前研究可知：在外載下巖體內的初始細觀損傷可以發展為宏觀損傷，而且從損傷的尺度問題與損傷識別的尺度問題來看，巖體的宏觀損傷與細觀損傷之間并無嚴格界限，它們通常與所研究問題的尺度有關。但是，為了工程分析方便，對巖體的宏觀損傷和細觀損傷進行分類研究，然后進行耦合計算分析是十分必要的[10]。為此，本文作者首先分別闡述基于細觀損傷和宏觀損傷的巖體損傷本構模型，進而根據Lemaitre應變等效假設建立綜合考慮宏觀和細觀缺陷的損傷變量(張量)，并由此建立相應的損傷本構模型。最后通過節理巖體的單軸壓縮試驗對該模型的合理性進行驗證。

1 考慮細觀缺陷的巖石損傷本構 模型

由于巖石是一種經過漫長地質年代形成的地質體，因此其內部隨機分布著各種各樣的缺陷。而統計損傷力學正是研究這些隨機缺陷的產生、擴展及匯合的過程及其對力學性質影響規律的有利工具，它將巖石內部損傷程度以微元強度加以量化，并根據巖石內部損傷服從隨機分布的特點，假定巖石內部缺陷服從某種分布，建立巖石損傷統計本構模型，使巖石統計損傷本構模型研究取得了很大進展[11?13]。目前該類模型的建立主要依據以下2方面：一是不同的巖石微元強度準則，如應變準則、Mohr?Coulomb準則、Drucker?Prager準則或Hoek?Brown準則等；二是認為巖石微元強度服從不同的分布，如冪函數分布、Weibull分布或對數正態分布等。研究表明基于Weibull分布的損傷模型要優于基于冪函數分布的損傷模型，且計算相對簡單[14]。因此，本文就采用基于應變強度準則和Weibull分布的損傷模型進行研究。

1.1 基于Weibull分布的損傷本構模型

假定巖石微元強度服從Weibull分布，其概率密度函數為[12]

式中：()為巖石微元強度分布函數；為微元強度隨機分布的分布變量，由于這里采用應變強度理論，因此這里指的是應變；和0為分布參數。

假設某一級荷載下已破壞的微元數目為，定義統計損傷變量為已破壞的微元數目與總微元數目之比。則：

式中：為巖石損傷變量；為某級荷載下已破壞的微元數目；為無損巖石材料的總微元數目。

當加載到某一水平時，破壞的微元數目為：

則損傷變量：

假定巖石微元破壞前服從廣義虎克定律，可得其本構關系為：

式中：和分別為無損巖石的彈性模量和應變。

根據廣義虎克定律，可得到基于Weibull分布的三維狀態下的巖石損傷統計本構模型：

1.2 分布參數的確定

式(6)變形后可得到：

然后兩邊取自然對數，可得：

顯然，式(8)為線性關系，為直線斜率，?ln0為截距，它們可通過對試驗數據的擬合而獲得。

2 考慮宏觀缺陷的巖體損傷本構 模型

節理等宏觀缺陷的存在將導致巖體力學性質的弱化及各向異性，為了反映這種影響，目前常采用損傷力學的方法進行研究。假定損傷后的巖體本構關系仍服從虎克定律，則節理對巖體的損傷就體現為彈性常數的弱化，即節理巖體的彈性常數與損傷張量之間的關系，可以表示為

其中：[0]和[]分別為完整巖塊和節理巖體的彈性張量；為單位張量；為節理巖體損傷張量。

因此節理巖體損傷本構模型的研究就歸結為損傷張量的計算。下面就以平面二維問題為例，討論節理巖體損傷張量的計算方法。目前常用二階張量描述節理巖體的各向異性損傷，許多學者基于不同角度也提出了多種不同定義方法。如Kyoya等[15]將含有一組平行節理的巖體損傷張量定義為

式中：為節理平均間距；為樣本體積；0為樣本中節理數；a為樣本中第條節理表面積；n為樣本中第條節理表面上的單位法向矢量。

孫衛軍等[16]假定節理面是一個無厚度、二維延展的圓盤，應用巖體結構的概率統計模型，可以估算節理巖體的損傷張量。例如對于第組節理，建議用下式表示其損傷變量：

式中：為第組節理面密度，條/m2；d為第組節理平均直徑，一般取為平面上的跡長；為第組節理的單位法向矢量。同時還有其他一些學者也提出了類似的節理巖體損傷變量計算方法。

上述節理巖體損傷變量的計算公式是針對含單組節理的巖體，而對于含有組節理的巖體，其總體損傷通常表示為：

而Swoboda等[17]認為應考慮裂紋組的非正交情形及其相互作用，進而基于能量原理推導了等效總體損傷張量的表達式：

3 考慮宏觀和細觀缺陷耦合的巖體損傷本構模型

3.1 宏觀和細觀缺陷耦合的損傷變量計算方法

根據損傷力學理論，損傷變量的定義是損傷模型建立的前提和基礎，因此下面首先討論同時考慮宏觀和細觀缺陷的節理巖體損傷變量。一般的工程巖體總是包含著節理、裂隙的宏觀損傷特性和節理間巖石的細觀損傷特性，這2種不同尺度損傷缺陷的耦合集中表現為損傷變量的耦合[10]。

在計算節理巖體損傷變量的耦合時，采用如下基本假設[10]：

1) 宏觀損傷與細觀損傷以人的肉眼可見與不可見劃分，并認為宏觀損傷為各向異性損傷，而細觀損傷為各向同性損傷。

2) 在描述巖體損傷時，細觀損傷和宏觀損傷分別采用不同的描述方法。

3) 在考慮宏觀和細觀損傷耦合時應遵循損傷力學的基本假設即Lemaitre假設，將應變等效原理進行耦合，而不能將2種損傷簡單地疊加。

損傷耦合的條件是在一定應力作用下，2種損傷分別引起的損傷應變之和等于耦合損傷引起的應變量，如圖1所示，假設圖1(a)~(d)所示分別為同時含有宏觀和細觀損傷的巖體、僅含宏觀損傷的巖體、僅含細觀損傷的巖體及完全不含損傷的巖體，其彈性模量分別為，，和0，其在外力作用下產生的應變分別為12，1，2和0，那么根據Lemaitre應變等效假設，則有：

(a)12；(b)1；(c)2；(d)0

圖1 應變等效計算示意圖

Fig. 1 Sketch map of calculation of equivalence strain

若假設宏、細觀損傷在荷載作用方向上造成的損傷變量分別為1和2及其耦合損傷變量為12，則有：

所以有：

由Lemaitre假設知：

將式(17)代入式(16)，并經過整理后可得：

對于2種極端情況，即巖體僅含宏觀損傷時，那么2=0，代入式(18)可得：12=1，即此時巖體的耦合損傷變量等于巖體的宏觀損傷變量，所以與實際情況符合。同樣當巖體僅含微觀損傷時，1=0，代入式(18)可得：12=2，即此時巖體的耦合損傷變量等于巖體的細觀損傷變量，也與實際情況符合。因此，這說明通過該方法建立的宏觀和細觀耦合損傷變量是合理的。

同樣基于Lemaitre假設，楊更社等[10]經過推導認為巖體的宏觀和細觀耦合損傷變量為

可以看出：對于式(19)，當1=0時，，即，也就是說當巖體內僅含細觀損傷時，巖體的總損傷變量即耦合損傷變量并不等于細觀損傷變量，顯然這與實際是不符的。通過對文獻[10]中的推導過程進行分析認為，它假設，是重復計算了一次完全無損傷彈性體產生的應變，即沒有減去圖1(d)中的試件所產生的應變，因而得出的結果也不甚合理。另外還有一些研究者也對巖體內不同尺度的損傷耦合問題進行了研究，如劉紅巖等[18]認為巖體宏觀和細觀耦合損傷變量應為：，但是從其建立過程來看，該方法缺乏嚴格的理論基礎。

下面對上述3種不同宏觀和細觀耦合損傷變量的計算結果進行對比分析，如圖2所示。

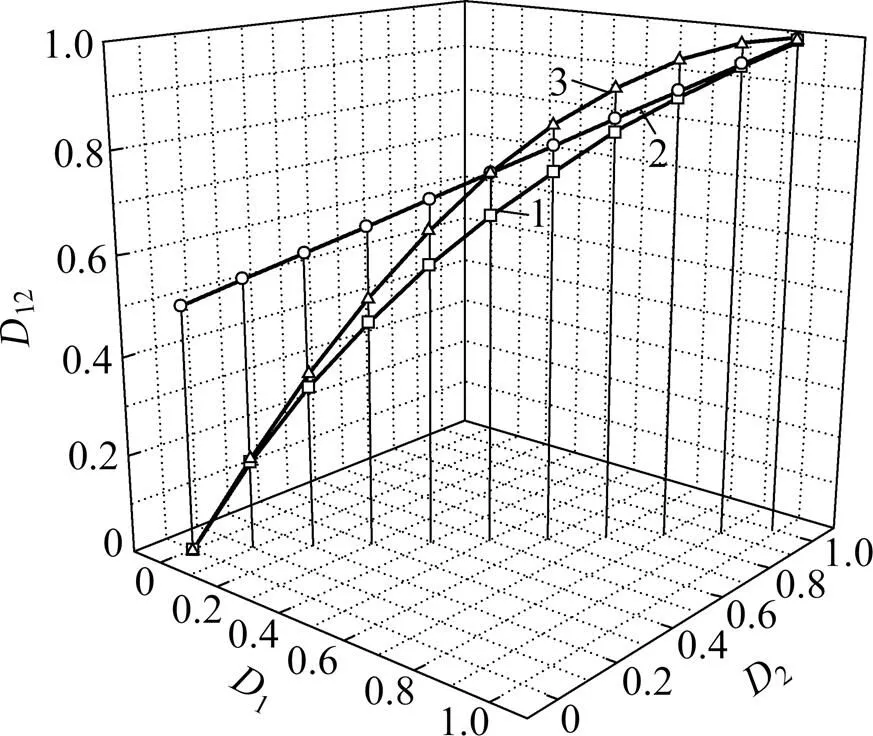
1—本文方法；2—文獻[18]方法；3—文獻[10]方法

由圖2可以看出：由本文方法計算出的耦合損傷變量最小，而隨著宏觀和細觀損傷變量的增加，由文獻[18]方法計算出的耦合損傷變量逐漸大于由文獻[10]方法的計算結果。這說明文獻[10]和[18]所提出的方法過大地估計了宏觀和細觀損傷的耦合影響，分析認為產生這種情況的主要原因是由于文獻[10]過大地估計了由損傷產生的應變，而文獻[18]則缺乏相應的理論基礎，因此認為本文所提出的計算方法是較為合理的。

由于宏觀損傷具有奇異性，前面所采用的1僅為荷載作用方向上的損傷變量值，因此必須對張量化以反映巖體宏觀損傷的各向異性。張量化的方法很多，在此采用Kawamoto等[21]的方法，引入損傷張量，則：=，式中是一個二階對稱張量，其計算方法為：

1) 對于含單組非貫通裂隙的巖體，假定非貫通裂隙的法向與軸夾角為，如圖3所示，設該組非貫通裂隙的單位法向矢量為，則有：

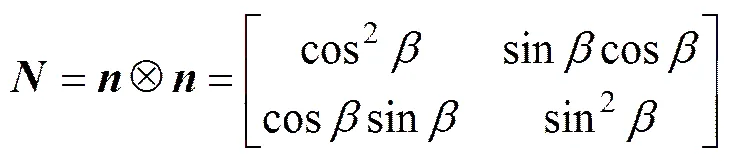
2) 對于含2組以上非貫通裂隙的巖體，的計算方法是：設巖體中有組非貫通裂隙，其單位法向矢量分別為=1，2，…，)，而，(，=1，2，3)。

根據上述方法，張量化后，式(18)即變為

若假設節理等宏觀缺陷引起的損傷張量為、微裂紋等細觀缺陷引起的損傷變量為，那么這2種不同尺度的缺陷所引起的耦合損傷變量12為

3.2 巖體損傷本構方程

由前述可知：節理巖體同時存在宏觀和細觀兩類缺陷，它們都起到了弱化巖體剛度和強度的作用，因此在節理巖體力學分析中應綜合考慮2種不同缺陷的共同作用。由于巖石中微缺陷造成的損傷是各向同性的，而宏觀節理、裂隙等造成的損傷卻是各向異性的，如以微元強度服從Weibull分布的損傷統計本構模型為例，那么根據損傷力學理論，則由式(21)所示的宏觀和細觀耦合損傷變量，則可得到考慮宏觀和細觀缺陷耦合的節理巖體損傷本構模型為

其中：為節理等宏觀缺陷引起的巖體損傷張量；為微裂隙等細觀缺陷引起的損傷變量；[0]為無損傷巖石的彈性張量。

4 算例分析

4.1 節理巖體應力應變計算

為了說明本文所建模型的合理性，引用文獻[19]的試驗資料對其進行驗證，這里對二維問題按照平面應力問題進行計算。巖石試件直徑×長度為50 mm×100 mm的紅砂巖標準試件，彈性模量及泊松比分別為6 949 MPa和0.22。其單軸壓縮試驗曲線如圖4所示。將彈性模量、泊松比及應力應變曲線試驗數據代入式(8)計算可得：=3.335 2，0=0.012 8。將分布參數以及實測試驗數據代入式(5)即可得到僅考慮細觀損傷時巖石的壓縮應力應變曲線，與試驗曲線的比較如圖4所示，可以發現二者吻合較好。

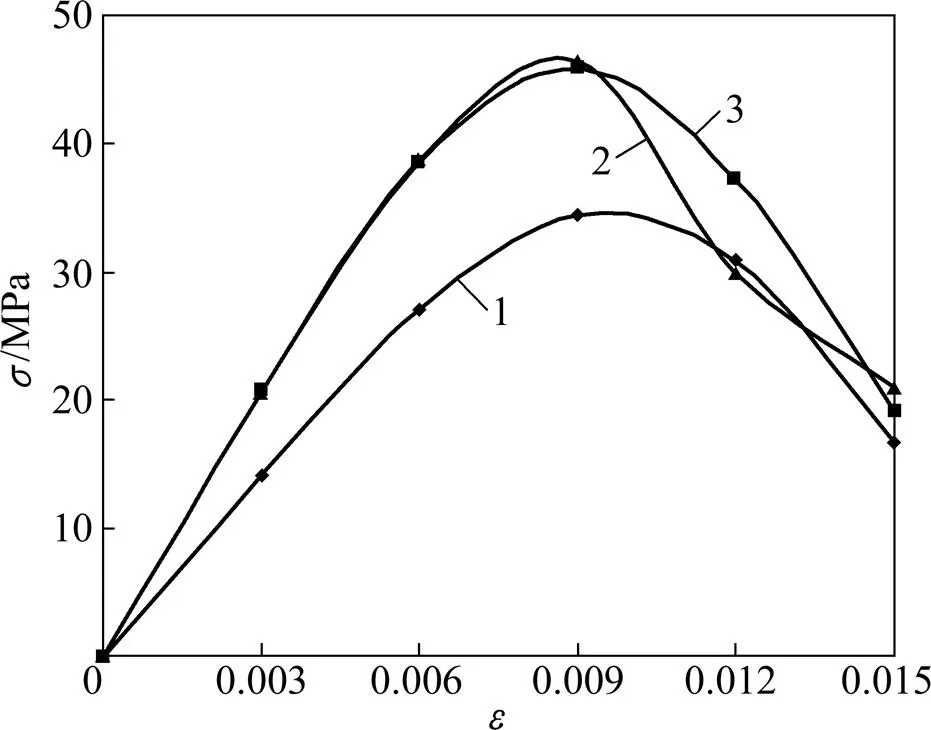
1—同時含宏觀和細觀缺陷的試件計算曲線；2—僅含細觀缺陷的試件實測曲線；3—僅含細觀缺陷的試件計算曲線

假設試件內存在一條宏觀節理，如圖5所示，那么它將對巖體產生各向異性損傷，這里采用式(11)計算其損傷張量。外裂隙的外法線方向為=[]，=200條/m2，d=0.071 m。計算可得其損傷張量為：，結合巖石的彈性常數0=6 949 MPa和=0.22，則根據式(22)，即可計算得到其垂直方向上不同軸向應變所對應的應力。由此得到考慮宏觀和細觀損傷耦合的應力應變曲線如圖5所示。由圖5可以看出：1) 當巖石內部僅含有細觀損傷時，基于Weibull分布的細觀損傷模型能夠較好地反映巖石的應力應變曲線特征，特別是在峰值強度之前，理論曲線與試驗曲線吻合很好；2) 從試件峰值強度來看，當巖體內含有節理等宏觀缺陷時，其力學性質明顯軟化，表現為在產生同樣的軸向應變時，所需應力大大減小。對本算例而言，含宏觀缺陷即節理的巖體，其峰值應力為34.35 MPa，僅為完整巖體峰值強度的74.8%，這說明節理存在大大削弱了巖體峰值強度，降低了其剛度，增大了其柔性；3) 從試件應力應變曲線的特征來看，同時含有宏觀和細觀缺陷的巖體即節理巖體的應力應變曲線在峰值應力以前與僅含細觀缺陷的巖體即宏觀完整巖體的應力應變曲線相差較大，而在峰值后二者差距逐漸縮小，最后二者的殘余強度基本相等。這實際情況較為一致，因為即使完整巖石試件在壓縮荷載作用下，經過峰值強度后也會有宏觀裂紋出現，如單軸壓縮荷載作用下試件的宏觀裂紋通常為剪切斜裂紋或張拉豎向裂紋，也就是說此時的巖體也是同時含有宏觀和細觀缺陷的試件，那么峰值應力后其力學性質也會同時受到宏觀和細觀缺陷的共同影響，因此會表現出與初始狀態下就含有宏觀和細觀缺陷的巖體相接近的力學性質，即有相似的殘余應力特征。圖6所示為其細觀損傷演化曲線。由圖6可以看出：當試件應變在0.003以前，其損傷基本上為零，即沒有損傷演化，同時從圖4所示的應力應變曲線圖上可以看出該段主要是對應著初始彈性階段。之后隨著應力增加，應變逐漸增大，同時損傷也呈現較大的增加趨勢，曲線斜率逐漸變大，尤其是在應變達到0.006以后，損傷增加較為迅速。而當試件達到峰值應變0.009時，其損傷僅為0.27，說明即使當試件到達峰值強度發生破壞后，仍有一定的殘余強度。同時需要說明的是，由于本文在提出的損傷模型中同時考慮了宏、細觀2種不同尺度的損傷，因此圖6中的損傷演化指的僅是細觀損傷演化，而不是試件的總體損傷演化。

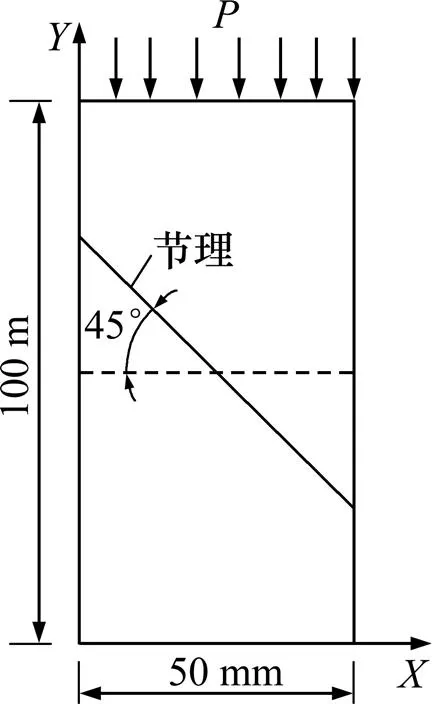
圖5 計算模型示意圖

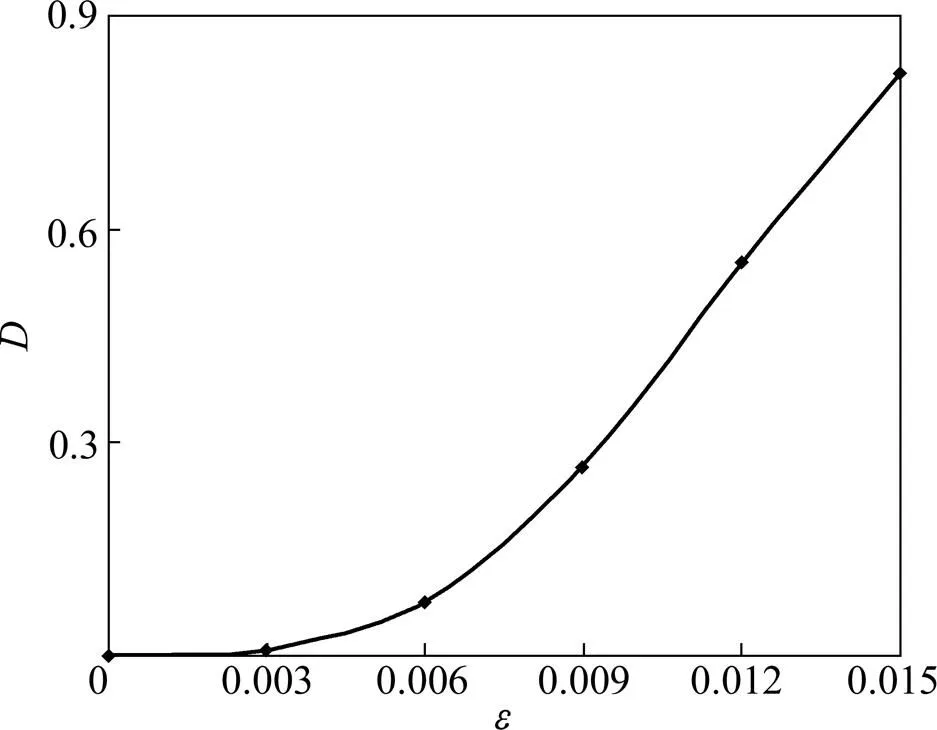
圖6 細觀損傷演化曲線

4.2 含不同傾角節理的巖體力學特性分析

下面應用上述模型分析節理傾角(指節理走向與水平面的夾角，采用單節理試件)對試件應力?應變關系的影響規律，如圖7所示。由圖7可知：當=90°即試件含一條貫通的垂直節理時，試件峰值強度最大為45.92 MPa，與完整試件的峰值強度基本相同。而當=60°時，試件峰值強度最小，僅為24.0 MPa，約為含90°節理試件強度的52.3%。而為45°和30°時試件的強度基本相等，均為27.0 MPa，約為含90°節理試件強度的56.8%。其強度變化規律與Jaeger等[20]的試驗結果十分類似，即隨著節理傾角在0°~90°變化時，試件單軸峰值抗壓強度呈開口向上的拋物線規律變化，即當節理傾角約為60°時，其單軸抗壓峰值強度最低，而90°時峰值強度最大，因此這也從另一側面說明了該模型的正確性。因此該計算結果表明節理傾角對巖體強度影響很大。

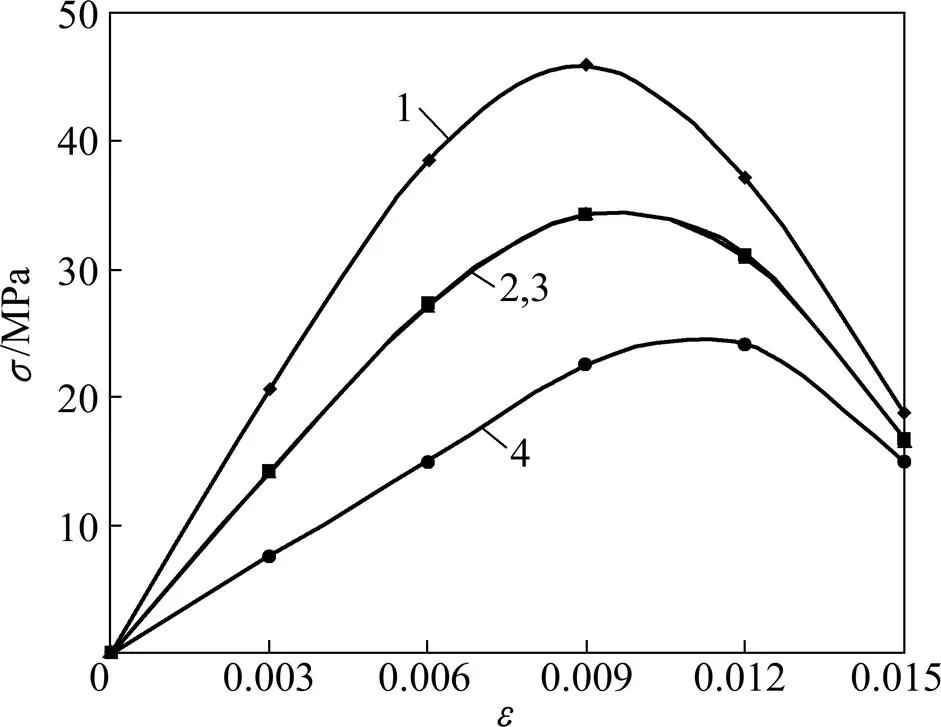
1—90°節理試件；2—30°節理試件；3—45°節理試件；4—60°節理試件

4.3 含多條節理的巖體力學特性分析

下面利用上述模型對含多條節理的巖體力學特性進行分析。采用的計算模型為圖5所示傾角為45°的節理試件，取平行節理條數=1~4條，計算結果如圖8和圖9所示。可以看出：1) 隨著節理條數增加，巖體應力應變曲線斜率降低，這說明巖體的彈性模量隨著節理條數的增加而降低，即節理巖體的變形增加，柔性變大；2) 隨著節理條數增加，巖體峰值強度逐漸降低，當節理條數為1~4時，對應的巖體峰值強度分別為34.35，21.94，12.40和7.14 MPa，相比相應完整巖石的峰值強度45.92 MPa均有不同程度的下降。且由圖9可以看出：隨節理條數增加，試件峰值強度的下降趨勢逐漸變緩。同時從下降幅度來看，當節理條數由1條增加到2條時，強度下降幅度最大，而當增加到3和4條時，強度下降幅度明顯減小，這說明節理之間存在著相互作用，作用結果將導致巖體的總體強度更加弱化，不符合單純的線性組合原理[21]；3) 隨著節理條數增加，試件峰值應變即峰值強度所對應的應變是逐漸增加的。這說明隨著節理條數增加，試件在破壞之前的變形越來越大，這主要因為在壓縮荷載作用下試件的總變形等于巖塊變形與節理面變形之和，而在壓縮荷載下節理面的閉合變形及剪切滑移變形量要比同等體積的巖塊大得多，因此隨著節理條數增加，試件在破壞前的總變形也將隨之增大。因此，該計算結果也說明上述模型是合理的。

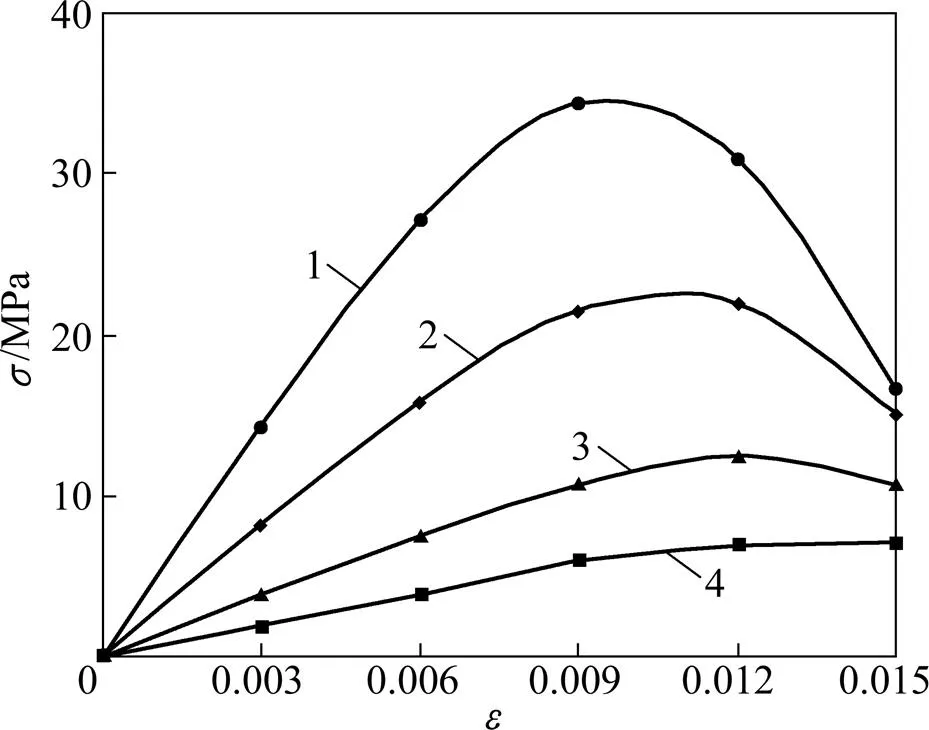
n：1—1；2—2；3—3；4—4

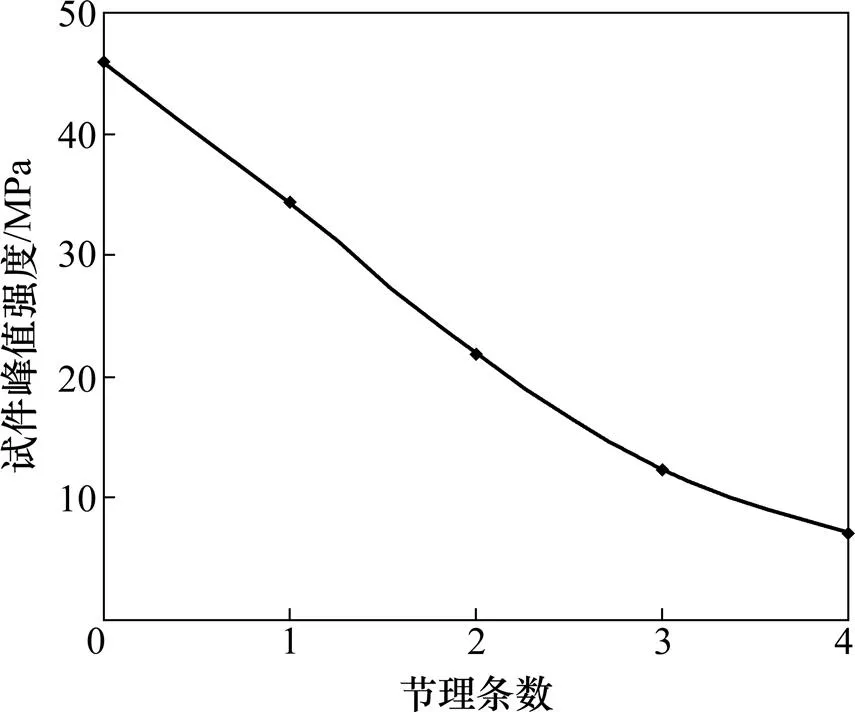
圖9 試件峰值強度隨節理條數的變化

5 結論

1) 基于節理巖體同時含有宏、細觀2種不同尺度缺陷的這一客觀事實，認為在其力學特性分析中應同時考慮上述兩類損傷的共同影響。并根據已有的宏、細觀損傷力學模型，建立了考慮宏觀和細觀缺陷耦合的節理巖體損傷本構模型。

2) 基于Lemaitre應變等效假設推導了考慮宏、細觀缺陷耦合的復合損傷變量，并與相關文獻中所提出的復合損傷變量進行了對比分析，說明了其合理性。

3) 通過引用相關的試驗資料對本文所提出的節理巖體損傷本構模型進行了初步驗證，表明本文提出的模型是合理的。同時通過算例表明，宏觀節理的存在大大削弱了巖體強度，降低了其剛度，且導致巖體力學性質呈現出明顯的各向異性。

4) 通過對含有不同傾角的單節理巖體試件和含多條平行節理的巖體試件的力學特性分析表明，當節理傾角在0°~90°之間時，巖體強度隨節理傾角呈開口向上的拋物線規律變化。隨著平行節理條數的增加，巖體強度逐漸降低，但降低幅度不同。

5) 本文所采用的算例為含貫通節理的巖體，因此未涉及在外力作用下節理擴展而導致的宏觀損傷演化問題，這有待進一步的深入研究。

[1] Wang T T, Huang T H. A constitutive model for the deformation of a rock mass containing sets of ubiquitous joints[J]. International Journal of Rock Mechanics & Mining Sciences, 2009, 46: 521?530.

[2] Halakatevakis N, Sofianos A L. Strength of a blocky rock mass based on an extended plane of weakness theory[J]. International Journal of Rock Mechanics & Mining Sciences, 2010, 47: 568?582.

[3] 劉紅巖, 黃妤詩, 李楷兵, 等. 預制節理巖體試件強度及破壞模式的試驗研究, 巖土力學, 2013, 34(5): 1235?1241.LIU Hongyan, HUANG Yushi, LI Kaibing, et al. Test study of strength and failure mode of pre-existing jointed rock mass[J]. Rock and Soil Mechanics, 2013, 34(5): 1235?1241.

[4] Tang C A. Numerical studies of the influence of microstructure on rock failure in uniaxial compression-PartⅠ: Effect of heterogeneity[J]. International Journal of Rock Mechanics & Mining Sciences, 2000, 37: 555?569.

[5] Zhou J W, Xu W Y, Yang X G. A microcrack damage model for brittle rocks under uniaxial compression[J]. Mechanics Research Communications, 2010, 37: 399?405.

[6] Xie N, Zhu Q Z, Xu L H, et al. A micromechanics-based elastoplastic damage model for quasi-brittle rocks[J]. Compters and Geotechnics, 2011, 38: 970?977.

[7] Kawamoto T, Ichikawa Y, Kyoya T. Deformation and fracturing behavior of discontinuous rock mass and damage mechanics theory[J]. International Journal of Numerical Analysis Method in Geomechanics, 1988, 12: 1?30.

[8] Grady D E, Kipp M E. The micromechanics of impact fracture of rock[J]. International Journal of Rock Mechanics & Mining Sciences, 1979, 16: 293?302.

[9] 劉紅巖, 邢闖鋒, 劉冶, 等. 宏微觀缺陷對巖體力學特性影響規律試驗研究[J]. 自然災害學報, 2013, 2(5): 134?139. LIU Hongyan, XING Chuangfeng, LIU Ye, et al. Test study on the law of macro and micro flaws effects on the mechanical properties of rockmass[J]. Journal of Natural Disater, 2013, 2(5): 134?139.

[10] 楊更社, 謝定義. 巖體宏觀細觀損傷的耦合計算分析[C]//第六次全國巖石力學與工程學術大會論文集. 武漢, 2000:327?329. YANG Gengshe, XIE Dingyi. Coupling analysis on the macro-damage and meso-damage of rock masses[C]// Symposium on the Sixth National Rock Mechanics and Engineering Academic Conference. Wuhan, 2000: 327?329.

[11] Krajcinovic D, Silva M A G. Statistical aspects of the continuous damage theory[J]. International Journal of Solids Structures, 1982, 18(7): 55?562.

[12] WANG Zhiliang, LI Yongchi, Wang J G. A damage-softening statistical constitutive model considering rock residual strength[J]. Computers & Geosciences, 2007, 33: 1?9.

[13] CAO Wengui, LI Xiang, ZHAO Heng. Damage constitutive model for strain-softening rock based on normal distribution and its parameter determination[J]. J Cent South Univ Technol, 2007, 14(5): 719?724.

[14] 岳洋. 基于不同分布的巖石損傷本構模型的比較[J]. 山西建筑, 2010, 36(24): 137?138. YUE Yang. Comparison of damage constitutive model of rock mass based on different distribution[J]. Shanxi Architecture, 2010, 36(24): 137?138.

[15] Kyoya T, Ichikawa Y,Kawamoto T. A damage mechanics theory for discontinuous rock mass[C]//Processings of the 5th International Conference on Numerical Methods in Geomechanics. Nagoya, Japan, 1985: 469?480.

[16] 孫衛軍, 周維垣. 裂隙巖體彈塑性-損傷本構模型[J]. 巖石力學與工程學報, 1990, 2(9): 108?119. SUN Weijun, ZHOU Weiyuan. An elasto-plastic damage mechanics constitutive model for jointed rockmass[J]. Chinese Journal of Rock Mechanics and Engineering, 1990, 2(9): 108?119.

[17] Swoboda G, Han B, Strumvoll M. Damage tensor theory and its application to tunneling[C]//Rossmanith H P. Mechanics of Jointed and Faulted Rock. Balkema, Rotterdam, 1990: 51?58.

[18] 劉紅巖, 呂淑然, 丹增卓瑪, 等. 節理巖體宏微觀損傷耦合的三維本構模型研究[J]. 水利與工程學報, 2013, 11(3): 85?88.LIU Hongyan, Lü Shuran, DANZENG Zhuoma, et al. Study on 3-D constitutive model for jointed rock mass by coupling macroscopic and microscopic damage[J]. Journal of Water Resources and Architectural Engineering, 2013, 11(3): 85?88.

[19] 凌建明, 孫鈞. 脆性巖石的細觀裂紋損傷及其時效特征[J]. 巖石力學與工程學報, 1993, 12(4): 304?312. LING Jianming, SUN Jun. On mesocrack damage of brittle rocks and its time-dependent characteristics[J]. Chinese Journal of Rock mechanics and Engineering, 1993, 12(4): 304?312.

[20] Jaeger J, Cook N. Fundamentals of rock mechanics[M]. London: Chapman and Hall Ltd, 1969: 100?105.

[21] 楊圣奇, 戴永浩, 韓立軍, 等. 斷續預制裂隙脆性大理巖變形破壞特性單軸壓縮試驗研究[J]. 巖石力學與工程學報, 2009, 28(12): 2391?2404. YANG Shengqi, DAI Yonghao, HAN Lijun, et al. Uniaxial compression experimental research on deformation and failure properties of brittle marble specimen with pre-existing fissures[J]. Chinese Journal of Rock mechanics and Engineering, 2009, 28(12): 2391?2404.

(編輯 楊幼平)

Damage constitutive model of jointed rock mass based on coupling macroscopic and mesoscopic flaws

ZHAO Yiqing1, LIU Hongyan2,3,4, Lü Shuran5, ZHANG Limin1,6

(1. School of Civil and Environmental Engineering, University of Science and Technology Beijing, Beijing 100083, China; 2. College of Engineering & Technology, China University of Geoseiences (Beijing), Beijing 100083, China; 3. School of Engineering, Tibet University, Lasha 850000, China; 4. Key Laboratory on Deep Geodrilling Technology, Ministry of Land and Resources, Beijing 100083, China; 5. School of Safety and Environment Engineering，Capital University of Economics and Business,Beijing 100026, China; 6. Hebei Chengde Iron and Steel Corporation, Chengde 067002, China)

The jointed rock mass damage constitutive model based on coupling of macroscopic and mesoscopic flaws was proposed. Firstly, the rock damage model which only considers the effect of mesoscopic flaws such as microcracks and the jointed rock mass damage model which only considers the effect of macroscopic flaws such as joints were introduced respectively. Secondly, the compound damage variable based on coupling the macroscopic and mesoscopic flaws was deduced based on the Lemaitre strain equivalence hypothesis, and then the damage constitutive model of jointed rock mass based on coupling macroscopic and mesoscopic flaws was set up. Finally, the rock uniaxial compression test data was adopted to validate this model. The results show that this model can perfectly reflect the effect of the two kinds of flaws on the rock mass stress?strain curve at the same time. Meanwhile, the stress?strain curves of the jointed rock mass with a single different dip angle joint and many parallel joints under uniaxial compression load are analyzed. The obtained results fit very well with the experimental and theoretical results in relevant references, which indicate the rationality of this model.

jointed rock mass; damage constitutive model; macroscopic flaw; mesoscopic flaw; damage coupling

10.11817/j.issn.1672-7207.2015.04.041

TU452

A

1672?7207(2015)04?1489?08

2014?04?04；

2014?06?16

國家自然科學基金資助項目(41002113，41162009)；教育部科學技術研究重點項目(211175)；中央高校基本科研業務費專項資金資助項目(2014ZY45)；2011年度北京市屬高等學校人才強教深化計劃人才創新團隊項目(PHR201107143)(Projects (41002113, 41162009) supported by the National Natural Science Foundation of China;Project (211175) supported by the Key Project of Chinese Ministry of Education; Project (2014ZY45) supported by the Fundamental Research Funds for the Central Universities;Project (PHR201107143) supported by the Funding Project for Academic Human Resources Development in Institutions of Higher Learning Under the Jurisdiction of Beijing Municipality)

劉紅巖，博士，教授，從事巖石力學方面研究；E-mail：lhyan1204@126.com