一種余數系統基擴展算法及VLSI實現

馬 上，汪陳浩，胡劍浩

?

一種余數系統基擴展算法及VLSI實現

馬 上，汪陳浩，胡劍浩

(電子科技大學通信抗干擾技術國家級重點實驗室 成都 611731)

基擴展是余數系統(RNS)在數字信號處理(DSP)系統中應用的關鍵問題之一。該文提出了一種新型基擴展算法，實現基為的余數系統到基為的余數系統的動態范圍擴展。給出其VLSI實現結構，并基于的特性對該結構進行了優化，使該實現結構僅由普通二進制加法器和模加法器構成。基于單位門模型和ASIC的性能對比分析結果表明，在實現相同動態范圍擴展時，該算法具有良好的VLSI實現性能。

基擴展; 數字信號處理; 余數系統; 超大規模集成電路

余數系統(residue number system，RNS)是一種非權重數值表征系統，它將傳統的較大位寬的乘加運算分解為多個較小位寬的并行通道進行處理，從而降低了復雜度和計算的關鍵路徑，可獲得高速、低功耗的VLSI(very large scale integrated circuits)實現性能。因此，近年來余數系統在乘加密集型的數字信號處理(digital signal processing, DSP)系統中得到了廣泛研究[1-3]。然而，在DSP系統的運算過程中，數值的動態范圍會隨著乘、加等基本運算而增加。這是RNS在DSP系統中應用面臨的基本問題之一，如何高效地實現RNS動態范圍的擴展對于其在DSP系統中應用有重要意義。

由于余數系統具有非權重的特性，故需要采用特殊的基擴展技術解決該問題。余數系統基擴展方法可以分為兩類：第一類保留原余數基，通過增加新的余數基分量來擴大余數系統的動態范圍[4-9]；第二類保留原余數系統的通道數量不變，通過增加原余數基的數據位寬來實現動態范圍的擴大。

目前關于余數動態范圍的擴展主要集中在第一類方法的研究上。文獻[4]提出了Szabo-Tanaka算法，該算法利用了混合基轉換(mixed radix conversion, MRC)和一個附加修正單元現基擴展，其實質為先做余數系統到二進制系統轉換(residue to binary，R2B)，恢復出原數據后再對新余數基求模，算法復雜度較高。文獻[5]討論了兩通道余數基向第三個余數基分量擴展的方法，同時，該算法可以推廣至基為的余數系統基擴展(其中為正整數)。文獻[6]在文獻[5]的基礎上提出了通用的兩通道余數系統向三通道余數系統的擴展方法。文獻[7]提出了以中國剩余定理(chinese remainder theorem, CRT)為基礎并結合冗余基實現第一類基擴展的通用方法，但計算中仍包含完整的R2B轉換。文獻[8]提出一種基于改進中國剩余定理來實現第一類基擴展的方法，該算法首先改進了中國剩余定理，并利用查找表(look-up table，LUT)實現基擴展，再基于改進后的CRT同時可以實現縮放操作，該算法不需要冗余基。文獻[9]提出了利用文獻[8]中基擴展算法實現縮放，并認為比文獻[4,7]提出的算法更加有效。

第一類基擴展方法的研究均采用余數系統后向轉換算法為理論基礎。在其實現中通常需要余數系統到二進制系統轉換和二進制到余數系統轉換(binary to residue，B2R)過程，算法復雜度太高。第二類余數基擴展方法則保留了原余數基的原有特點，僅增加各通道的位寬，保留了原余數基運算通道的電路結構，且不需要考慮擴展基與原始基的互質條件。另一方面，在DSP應用中如乘法級聯為特征的離散付氏變換、離散余弦變換和離散小波變換等，需要方便高效地將余數通道的數據位寬擴大一倍。因此，第二類基擴展具有重要的應用價值，目前對這一方法的研究還較少。

1 背景知識

1.1 余數系統與混合基轉換

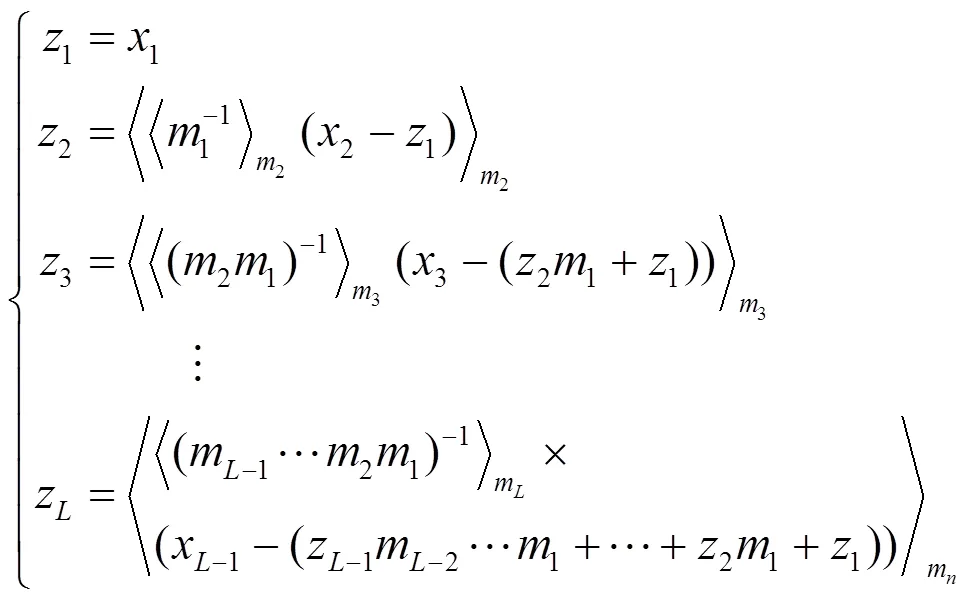
1.2 基擴展定義

2 余數通道數據位增加的基擴展算法及其VLSI實現結構

(2)

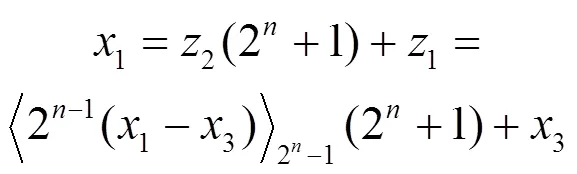
對于式(3)，可進行適當優化，以簡化VLSI實現結構。對于，有：

(4)

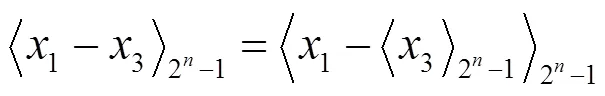
(6)

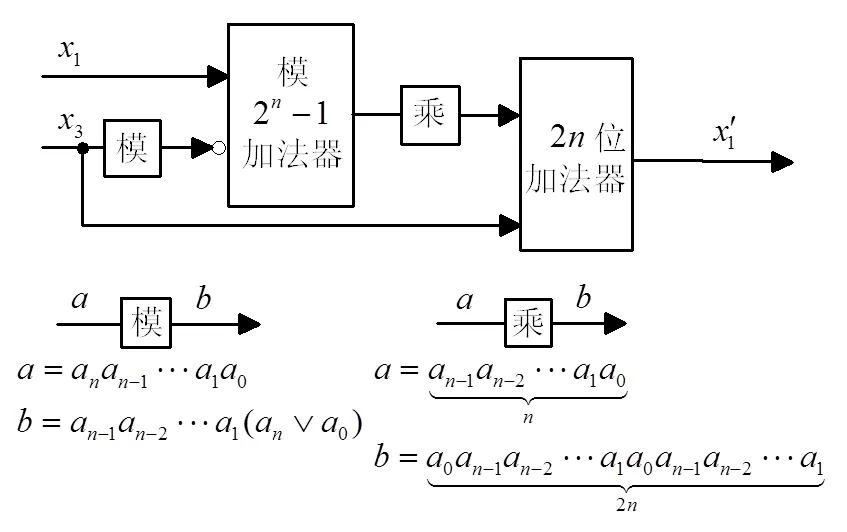
圖1 通道擴展VLSI實現結構

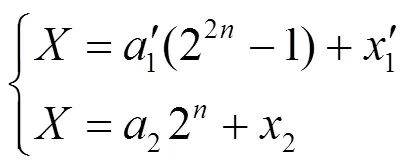
(8)

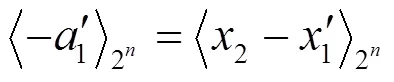
(10)

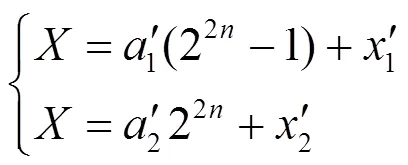
(12)

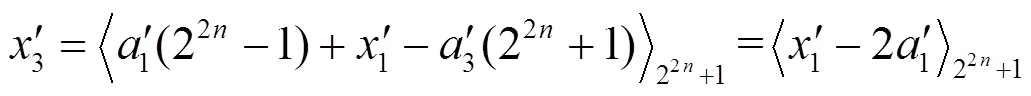
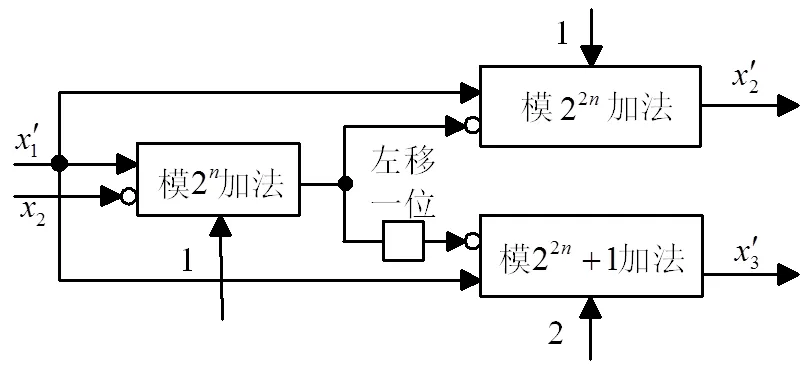
圖2 及通道擴展VLSI實現結構

由此，3個模減法器均轉化為模加法器，具體實現電路如圖2所示，其電路結構非常簡單。

由2.1節和2.2節的分析可知，本文的擴展算法中，需先擴展出通道的值，然后擴展出其他兩路的值，其整體實現框圖如圖3所示。

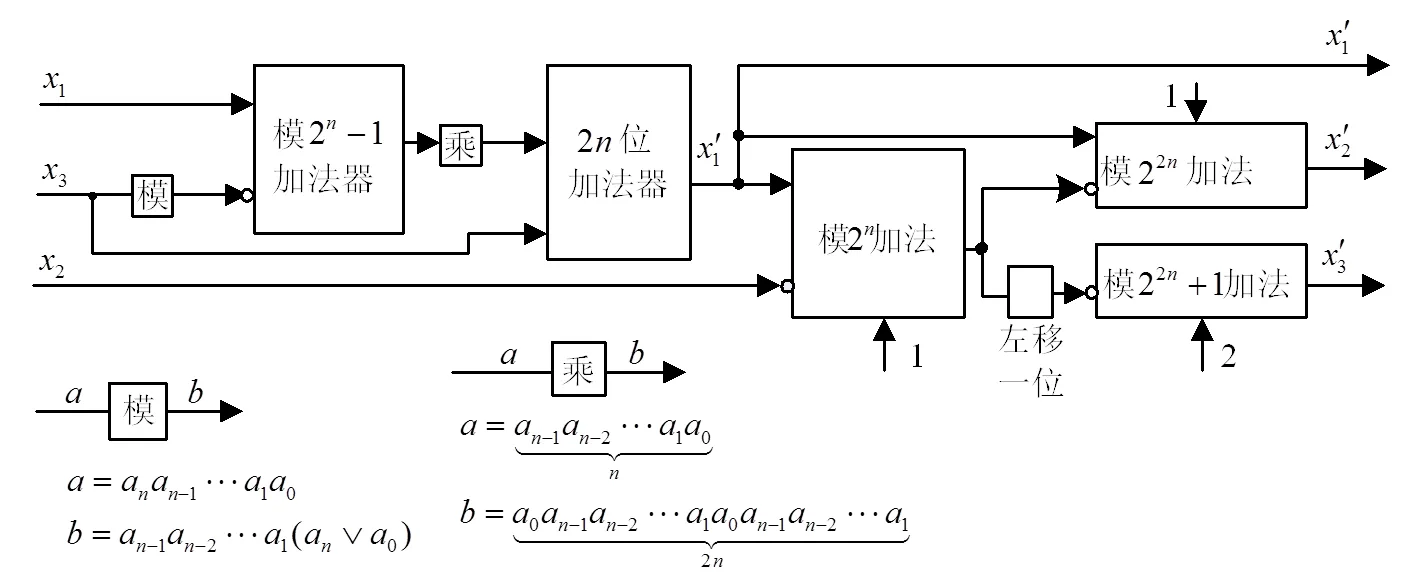
圖3 整體設計VLSI實現結構

3 性能分析與對比

3.1 性能分析

綜上所述，本文提出的基擴展需要的面積和關鍵時延分別為：

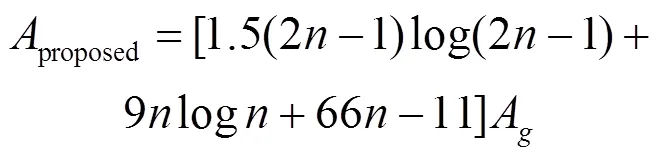
(15)

3.2 性能對比

對于Szabo-Tanaka算法，文獻[7]及文獻[8]均為第一類基擴展，而本文提出的算法為第二類基擴展。限定原始余數基均為，并設其擴展出的余數基分量為，那么可在擴展相同的比特位寬條件下進行性能對比。

表1給出了本文算法、Szabo-Tanaka算法，文獻[7]及文獻[8]提出的算法在擴展比特位寬的條件下的硬件消耗、時延性能對比(基于單位門模型)。

在集成電路實現中，查找表中每比特存儲單元所需CMOS管為6個[15]，而相對應的單位門模型中簡單門同樣需要6個CMOS管，故可大致認為查找表中每比特存儲單元的面積消耗對應于單位門模型的面積為；同時可設查找表的平均查找時延為。據此，可將查找表的硬件、時延性能轉換為單位門模型進行分析。

表1 硬件性能及擴展基對比

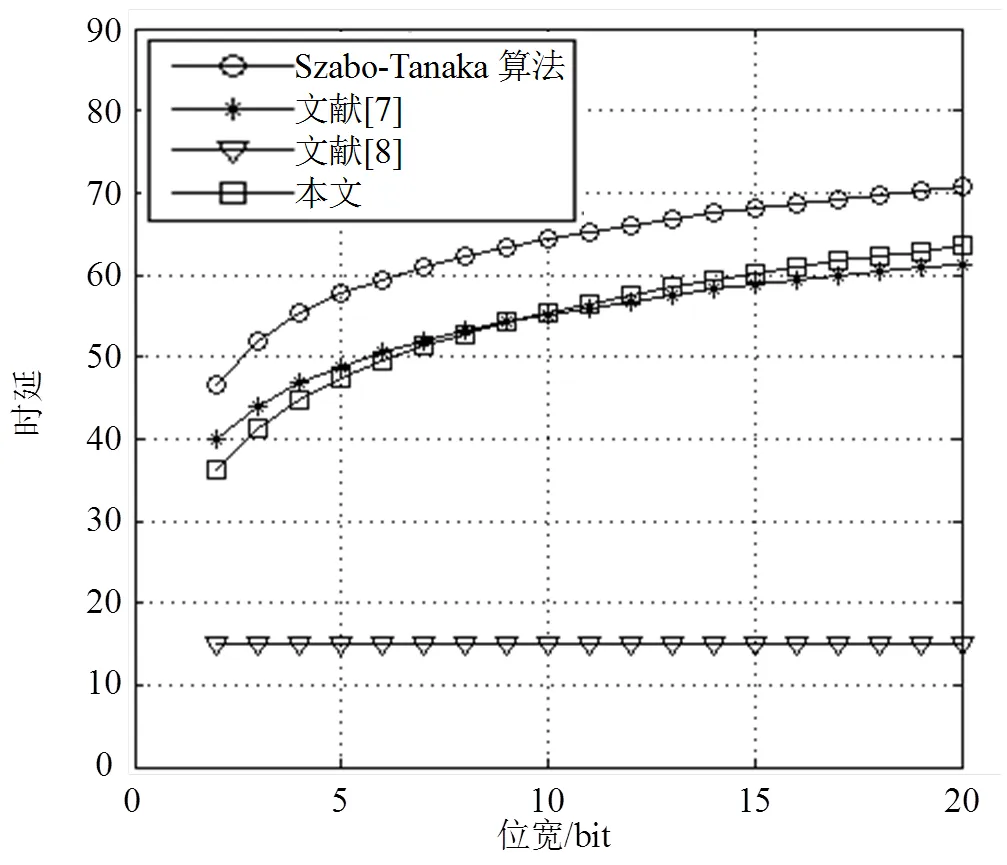
圖4 基于單位門模型的時延對比

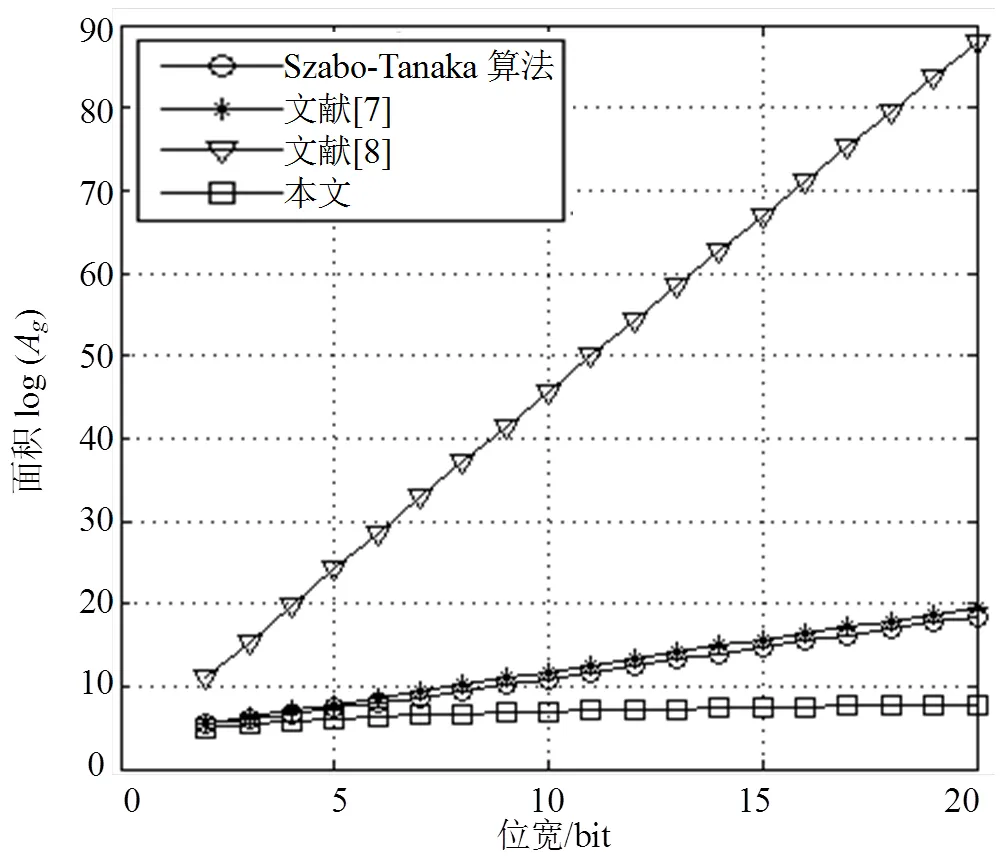
圖5 基于單位門模型的面積對比

由于Szabo-Tanaka算法為較經典的第一類基擴展算法，其他第一類基擴展算法大多基于該思想進行設計，因此其對第一類基擴展算法具有較好的代表性。為了進一步進行性能分析和對比，基于VHDL語言對本文所提出的基擴展算法和經典的Szabo-Tanaka算法進行設計，其中所需的模加法器的設計采用了端回進位法，模加法器設計采用了消“1”法。然后利用Synopsys公司的Design Compiler對這些設計進行面向ASIC的綜合，綜合中采用了DC的Class庫，工藝為SMIC 130 nm，電壓設置為1.08 V，溫度為125 ℃。DC實現結果如表2所示。

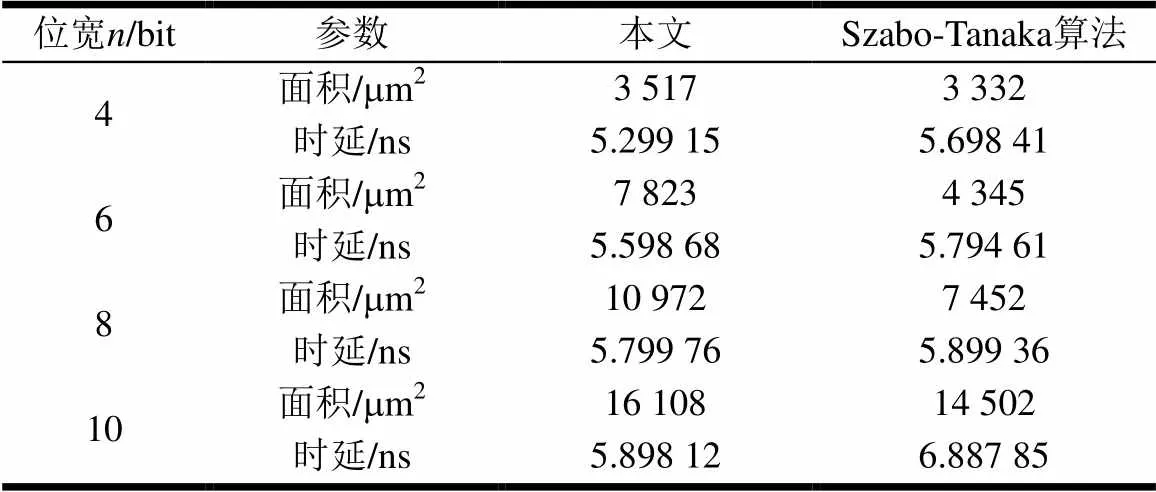
表2 ASIC綜合結果

由表2可見，本文提出的基擴展方法在時延方面占有較大優勢，但面積與理論分析較為不同，分析原因是由于Szabo-Tanaka算法中的模加法器形式較為統一，因此綜合軟件采用了較多的復用，從而使得實際綜合面積比理論分析面積小。

4 結 論

[1] CONWAY R, NELSON J. Improved RNS FIR filter architectures[J]. IEEE Transactions on Circuit and Systems II, 2004, 51(1): 26-28.

[2] MADHUKUMAR A S, CHIN F. Enhanced architecture for residue number system-based CDMA for high-rate data transmission[J]. IEEE Transactions on Wireless Communications, 2004, 3(5): 1363-1368.

[3] MA Shang, HU Jian-hao, LING Xiang, et al. The applications of RNS in SDR systems[C]//2008 International Workshop on Software Radio Technology (SRT2008). Beijing: [s.n.], 2008: 49-54.

[4] SZABO N S, TANAKA R I. Residue arithmetic and its applications to computer technology[M]. New York: McGraw-Hill, 1967.

[5] O’KEEFE K H, WRIGHT J L. Remarks on base extension for modular arithmetic[J]. IEEE Trans Comput, 1973, 22: 833-835.

[6] O’KEEFE K H. A note on fast base extension for residue number systems with three moduli[J]. IEEE Trans Comput, 1975, 24: 1132-1133.

[7] SHENOY A P, KUMARESAN R. Fast base extension using a redundant modulus in RNS[J]. IEEE Trans Comput, 1989, 38: 292-296.

[8] BARSI F, PINOTTI M C. Fast base extension and precise scaling in RNS for look-up table implementations[J]. IEEE Trans Signal Processing, 1995, 43: 2427-2430

[9] LAI Yu-feng, KONG Yi-nan. An implementation of a scaler in the residue number system[C]//International Symposium on Communications and Information Technologies. [S.l.]: [s.n.], 2012: 529-532

[10] WANG Yu-ke. New Chinese remainder theorems[C]// Conference Record of the Thirty-Second Asilomar Conference on Signals, Systems & Computers. Pacific Grove: [s.n.], 1998, 1: 165-171.

[11] MA Shang, HU Jian-hao, ZHANG Lin, et al. An efficient RNS parity checker for moduli setand its applications[J]. Science in China Series F: Information Sciences, 2008, 51(10): 1563-1571.

[12] MA Shang, HU Jian-hao, WANG Chen-hao. A novel moduladder for residue number system[J]. IEEE Transactions on Circuits and Systems-I, 2013, 60(11): 2962-2972.

[13] PATEL R A, BOUSSAKTA S. Fast parallel-prefix architectures for moduloaddition with a single representation of zero[J]. IEEE Trans on Computers, 2007, 56(11): 1484-1492.

[14] EFSTATHIOU C, VERGOS H T, NIKOLOS D. Fast parallel-prefix moduloadders[J]. IEEE Trans on Computers, 2004, 53(9): 1211-1216.

[15] WESTE H E, HARRIS D M. CMOS VLSI Design[M]. 2nd ed. [S.l.]: Addison Wesley, 2005.

編 輯 稅 紅

A New Base Extension Algorithm and VLSI Implement for Residue Number System

MA Shang, WANG Chen-hao, and HU Jian-hao

(National Key Laboratory of Science and Technology on Communications, University of Electronic Science and Technology of China Chengdu 611731)

The base extension operation for residue number systems (RNS) plays an important role in RNS-based digital signal processing (DSP) systems. In this paper, a new base extension algorithm is proposed which can extend the dynamic range from moduli setto moduli set. In this paper, the very large scale integrated (VLSI) circuits implement of the proposed algorithm is also presented, with the properties of moduli set, the implement is composed of binary adders and modular adders; The analysis result based on unit-gate model and ASIC (application specific integrated circuit) implementation shows that the VLSI implementation of the proposed base extension algorithm exhibits better performances for the same dynamic range extension.

base extension; digital signal processing; residue number system; VLSI circuits

TP33

A

10.3969/j.issn.1001-0548.2015.02.008

2013-09-04；

2015-01-21

國家自然科學青年基金(61101033)；特殊環境機器人技術四川省重點實驗室開放基金(13zxtk02)

馬上(1978-)，男，博士，副教授，主要從事電路理論、通信信號基帶處理等方面的研究.