動態環境下基于改進蟻群算法的機器人路徑規劃研究

屈 鴻，黃利偉，柯 星

?

動態環境下基于改進蟻群算法的機器人路徑規劃研究

屈 鴻，黃利偉，柯 星

(電子科技大學計算智能實驗室 成都 611731)

針對動態復雜條件下的移動機器人路徑規劃問題，根據全局靜態環境先驗知識，提出一種改進蟻群算法。在經典蟻群算法的基礎上通過調整轉移概率，限定信息素強度的上下界，并引入相關策略解決死鎖問題，可以避免初期規劃的盲目性，增加解的多樣性，提高算法的全局搜索能力，進一步減小算法早熟的可能性。在規劃過程中，根據動態障礙物運行方向的變化與否，提出了相應的碰撞避免策略，并針對環境突發狀況引入Follow_wall行為進行改進。仿真實驗證明，該算法優于經典蟻群算法，可有效地指導移動機器人避免環境中的動態障礙物，獲取無碰最優或次優路徑，并能更好地適應環境的變化。

蟻群算法; 動態復雜環境; 移動機器人; 路徑規劃

在給定運行空間中，移動機器人路徑規劃的主要目標是通過一定的算法尋求一條從起始位置到目標位置的最優或次優無碰路徑。目前針對全局信息已知的靜態環境下移動機器人路徑規劃的研究已經很成熟。但是如何在有動態障礙物的環境背景下進行移動機器人路徑規劃仍是一個難題。

1 環境描述

設二維平面上的矩形區域E為機器人的運行環境空間。對機器人運行環境空間的建模采用柵格法，且其中同時存在靜態和動態障礙物。靜態障礙物可以是任意形狀，且數量有限；動態障礙物為圓形且數量有限。若靜態障礙物只占據某個柵格的一部分，則將其視為完全占據此柵格。此外對移動機器人運行環境和移動機器人本身做出以下假設：

2) 環境中靜態障礙物位置信息已知，并進行“膨化”處理，以確保靜態障礙物邊界為安全區域。

3) 環境中動態障礙物視為圓形，其直徑為單個柵格寬度(即為1)且其速度固定，但方向不定，不會和環境中的靜態障礙物及邊界發生碰撞。

4) 移動機器人能夠通過傳感器感知有限范圍環境中動態障礙物的運行速度和方向。

5) 移動機器人和動態障礙物的可移動方向如圖1所示。

6) 移動機器人可在勻速運動與暫停兩種運行狀態下任意轉換。

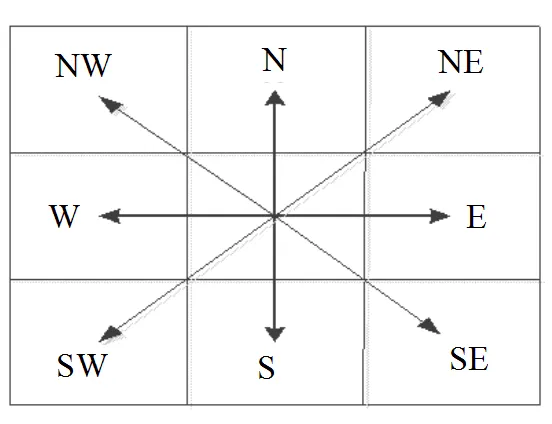
圖1 移動機器人和動態障礙物可移動方向示意圖

2 經典蟻群算法的改進

蟻群算法[1]提出至今，國內外學者對其進行了大量的研究，并已被廣泛地應用于解決旅行商問題[2]、路由問題[3]、工件排序問題[4]、車輛運輸調度問題[5]、圖著色問題[6]、機器人路徑規劃問題[7-8]。

經典蟻群算法中螞蟻通過向著信息素濃度較高的路徑移動來尋找最優路徑，這種正反饋機制可以加快收斂速度，但會導致蟻群多樣性減小，全局搜索能力減弱。此外在一些比較復雜的環境下，蟻群算法可能進入死鎖狀態。為保證蟻群算法能夠收斂到全局最優或近似最優并解決死鎖問題，針對其存在的不足之處，本文做出以下的改進。

1) 調整轉移概率

在經典蟻群算法的轉移概率基礎上引入隨機選擇機制以增加解的多樣性。操作如下：設置隨機選擇參數，及隨機數。如果，查看當前節點周圍所有節點的信息，排除有障礙物節點和已走節點后，隨機選取任意一個節點作為可行節點；如果，則需要計算轉移概率，然后根據轉移概率值來選擇下一個可行節點。新的可行節點選取為：

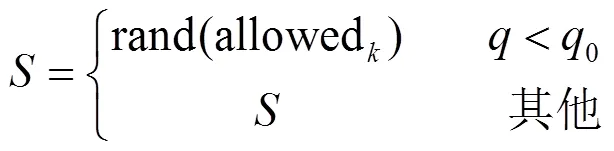
(2)

2) 信息素閾值限定

為進一步提高算法的全局搜索能力，借鑒最大最小螞蟻系統(MMAS)，在算法每次迭代中，全局更新最優路徑上的信息素時，對其進行上下界限定。限定公式為：

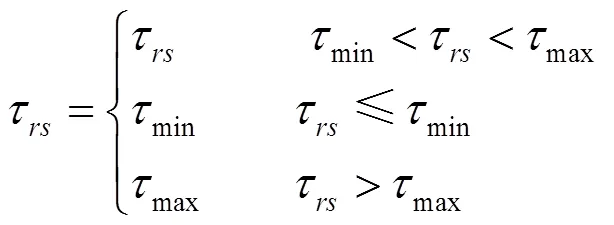
3) 死鎖問題處理

當環境條件較為復雜時，移動機器人可能陷入死鎖狀態。如圖2所示，機器人運行到時，無法向其周圍任意位置移動，即陷入死鎖狀態。

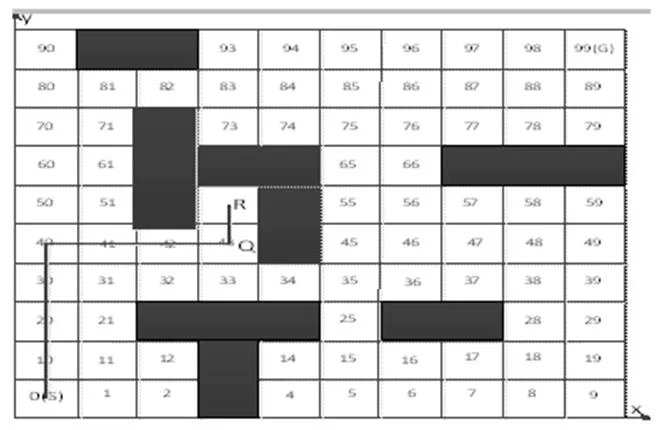
圖2 移動機器人進入死鎖狀態

針對死鎖問題，文獻[9]采取“早期死亡”(early death)方法，該方法的主要思想為令處于死鎖狀態的螞蟻死亡，且不對其已走路徑的信息素進行更新。但當有較多螞蟻陷入死鎖狀態時，該方法不利于全局最優解的搜索且會減小解的多樣性。對此，本文的解決方法如下：當螞蟻陷入死鎖時，允許其回退一步，不令其死亡，然后更新禁忌表信息，并對死鎖邊上信息素進行懲罰，在當前路徑上螞蟻重新選擇移動節點，如此即可避免其他螞蟻陷入死鎖。信息素懲罰函數為：

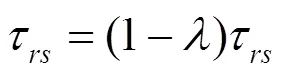
3 基于改進蟻群算法的路徑規劃

綜上所述，具體的改進蟻群算法流程如下：

1) 對環境的建模采用柵格法，并初始化移動機器人起始位置和目標位置及相關參數。

3) 若螞蟻在搜索路徑時陷入死鎖狀態，則采取死鎖問題處理方法。若目標點到達，則令，隨后轉到步驟2)，直到此次迭代過程中每一只螞蟻的搜索都已完成時結束，此時。

對應的流程圖如圖3所示。

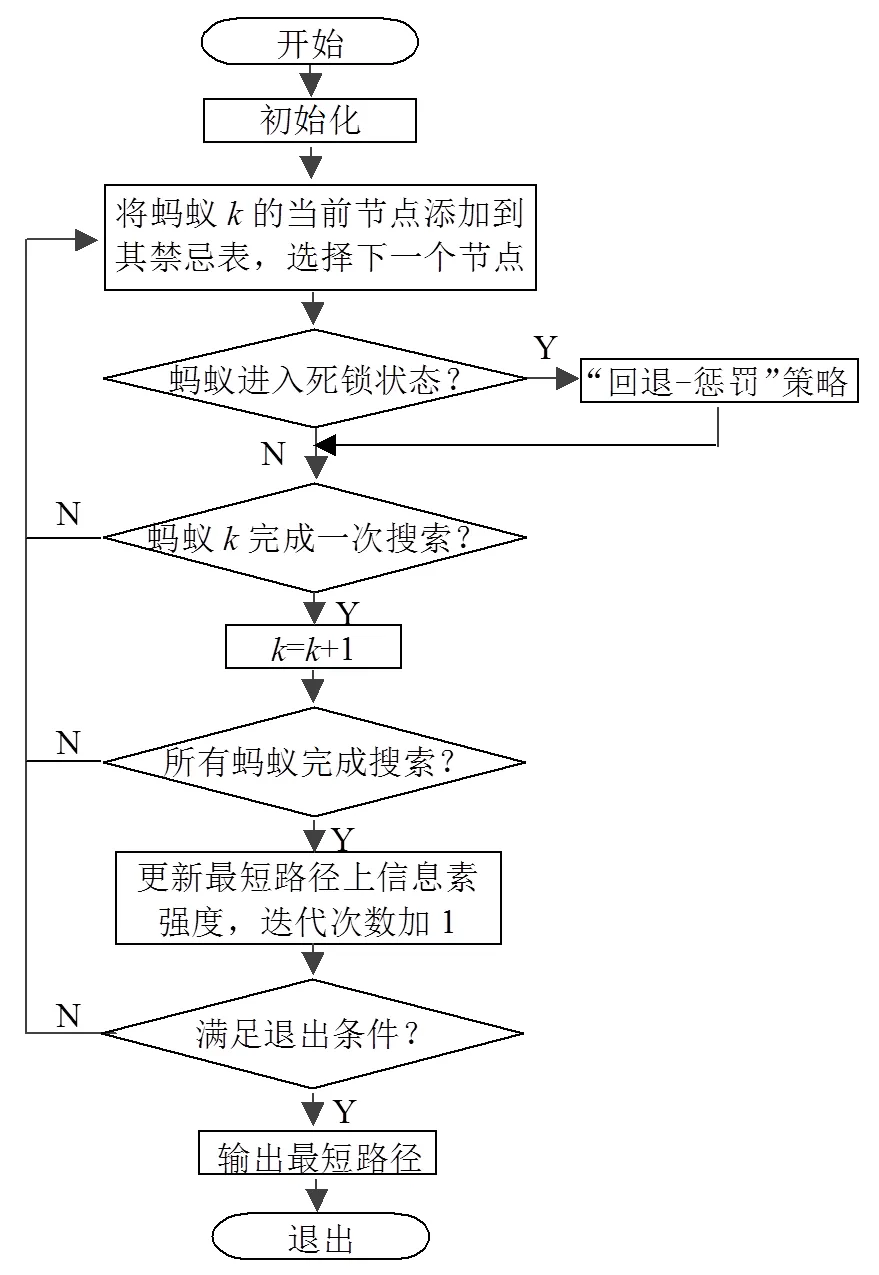
圖3 改進蟻群算法流程圖

4 動態環境避碰規劃策略

4.1 直線運動障礙物預測避碰

若環境中存在直線運動的障礙物，模擬滾動窗口，預測移動機器人與動態障礙物在一個滾動窗口周期內的運行軌跡，通過判斷它們是否相交來判斷碰撞是否發生，相應的碰撞避免策略如下：

1) 若移動機器人與動態障礙物無碰撞，則其按原始路徑移動一個步長進入下個滾動窗口；

2) 若移動機器人與動態障礙物發生側面碰撞，則其在到達碰撞點之前停頓時間，隨后繼續按原始路徑行進。的值為：

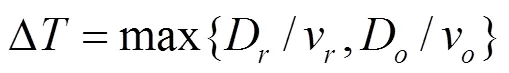
3) 若兩者發生正面碰撞，則重新規劃一條局部路徑。

①將滾動窗口邊界與原始路徑的交點所在柵格設為局部子目標。

②視碰撞處柵格為靜態障礙物，然后由當前位置至局部子目標點，利用改進蟻群算法獲得無碰最優局部路徑。

4) 再次根據相應策略進行預測避碰，此次將移動機器人置于規劃好的局部路徑中。

但當環境條件較為復雜時，“局部子目標不可達”的現象可能會出現。如圖4所示，在位置處，機器人在當前滾動窗口內探測到動態障礙物的存在，且將在點處發生正面碰撞。若根據上述步驟進行規劃，則無法規劃出局部路徑。

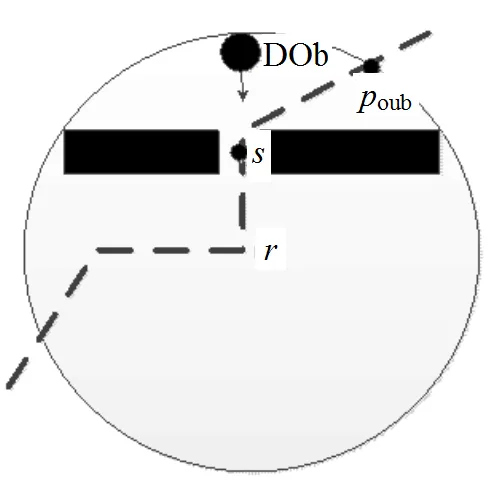
圖4 局部子目標不可達

針對以上問題，本文采用如下方法：

1) 機器人不再規劃局部路徑，通過改進蟻群算法將發生碰撞處柵格視為靜態障礙物獲得一條新的全局路徑。

2) 機器人將規劃出來的新的路徑作為原始路徑，并沿此路徑進行局部路徑規劃。

4.2 運行方向不定障礙物預測避碰

針對動態障礙物運行方向不確定的情況，文獻[10]中的策略(以下稱為策略一)是對動態障礙物進行膨化處理后，視整個膨化區域為靜態障礙物，然后通過判斷移動機器人的運行軌跡是否與膨化區域相交來判斷碰撞是否存在，進而進行局部路徑規劃，但該做法具有很大的保守性。對此，本文提出一種新策略(以下稱為策略二)來避免移動機器人與動態障礙物發生碰撞，兩種策略的性能比較在仿真實驗部分給出。

策略二的主要步驟如下：

1) 若預測到碰撞可能發生，則將時間分為等份，即，對應時間內移動機器人的步長為。

4) 按照步驟3)規劃出的局部路徑，移動機器人行進并進行預測避碰。

本文的策略能夠減小碰撞可能發生時的動態障礙物的膨化區域，從而可以提供更好的規劃路徑，進而對移動機器人進行有效的指導。兩種策略的對比分析在仿真實驗部分給出。

4.3 局部滾動預測避碰算法

結合上述碰撞避免策略和滾動窗口原理，本文提出局部滾動預測避碰算法，其主要步驟如下：

1) 相關參數初始化，主要有起始位置、目標位置、機器人步長以及滾動窗口半徑，并根據環境先驗知識不考慮動態障礙物，由改進蟻群算法規劃全局路徑Gpath。

2) 機器人按全局路徑以滾動窗口方式行進，刷新當前所在滾動窗口內的環境信息，判斷其是否到達目標點，若到達，則算法終止。

3) 在滾動窗口內進行碰撞檢測，若無碰撞，機器人按原始路徑移動一個步長，轉步驟2)。

4) 根據碰撞避免策略，規劃局部路徑Lpath，機器人沿此路徑行進，轉步驟2)。

首先由改進蟻群算法規劃出一條全局路徑，然后根據實時的局部環境信息，將預測避碰策略用于滾動窗口內，進行局部滾動預測避碰。由此避免與所有動態障礙物碰撞，隨滾動窗口逐步推進目標點，最終獲取無碰最優或次優路徑。

5 仿真實驗

5.1 改進蟻群算法性能比較

本文的實驗對比了改進蟻群算法和經典蟻群算法并驗證了其對死鎖問題的處理。蟻群算法相關參數如表1所示，經典蟻群算法無懲罰系數設置，實驗環境為VC++6.0。圖5為兩種蟻群算法規劃出的全局路徑。圖6為運行過程中兩種蟻群算法在最短路徑長度和收斂速度兩方面性能的比較。兩種算法分別運行100次后，各指標的統計結果如表2所示。

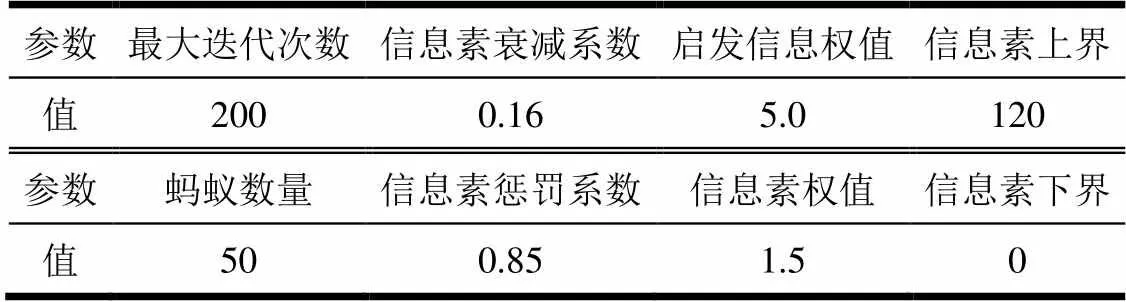
表1 改進蟻群算法相關參數設置

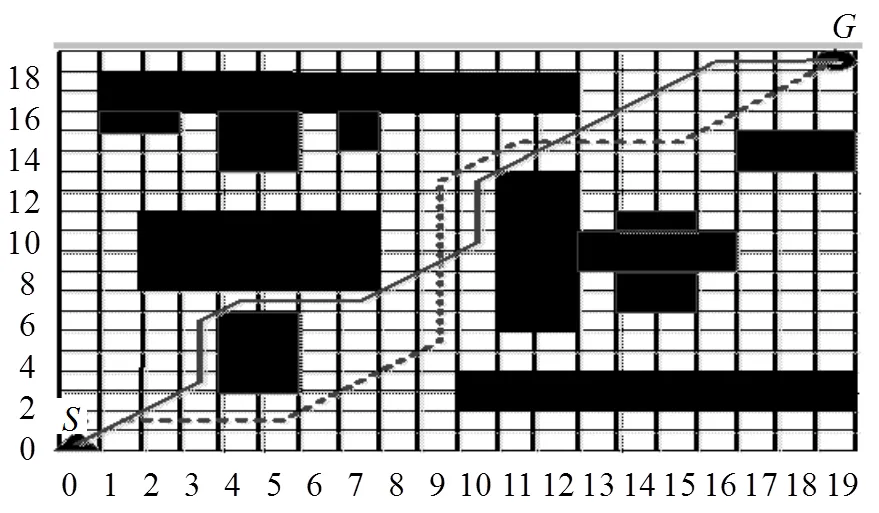
圖5 經典蟻群算法與改進蟻群算法路徑規劃結果

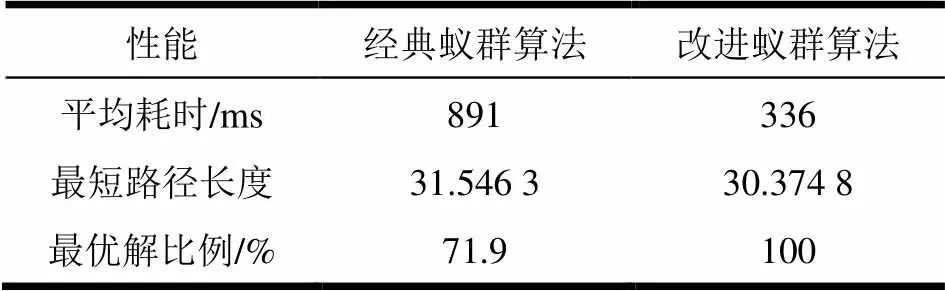
表2 經典蟻群算法與改進蟻群算法性能比較

由改進蟻群算法獲取的全局無碰最優路徑如圖5中實線所示，而由經典蟻群算法獲取的全局無碰最優路徑為圖5中的虛線路徑。

圖6中數據顯示出改進蟻群算法的收斂速度比經典蟻群算法要快，而且這兩種算法所獲取的最短路徑長度前者優于后者。

由表2得出，改進蟻群算法與經典蟻群算法相比，其最短路徑長度、最優解比例以及平均耗時都有一定的提升。在改進蟻群算法條件下，沒有螞蟻進入死鎖狀態且所有螞蟻都獲得了最優路徑，這一點可以從最優解比例為100%得出。同時說明改進蟻群算法可以有效避免死鎖問題。由以上實驗數據得出，相比于經典蟻群算法，改進蟻群算法可以加快收斂速度，時間性能也有所提升，并且能有效地避免局部最優和死鎖問題。

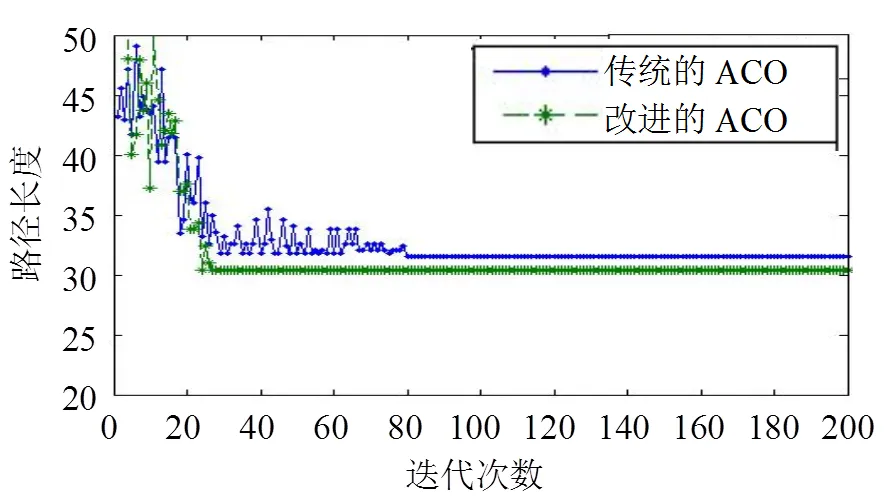
圖6 經典蟻群算法與改進蟻群算法收斂速度和最短路徑長度比較

5.2 動態環境下改進蟻群算法的可行性

本文的仿真實驗驗證了環境空間中存在動態障礙物時，由本文提出的改進蟻群算法所規劃出路徑的可行性。

仿真實驗中，環境運行區域被劃分為100′80的柵格，移動機器人起始位置坐標為，目標位置坐標為，步長為，感知半徑為。此外，環境中存在4個動態障礙物、、和，其中和做直線運動，和運動方向不確定，且每經過一個柵格后，移動方向隨機變化。動態障礙物移動步長為2。機器人運行環境如圖7所示，實驗環境為VC++6.0。

首先由改進蟻群算法根據靜態全局環境的先驗信息且不考慮動態障礙物的情況下，規劃出一條全局最優路徑，然后移動機器人按此路徑行進并進行預測避碰。規劃的全局路徑如圖7中虛線所示。

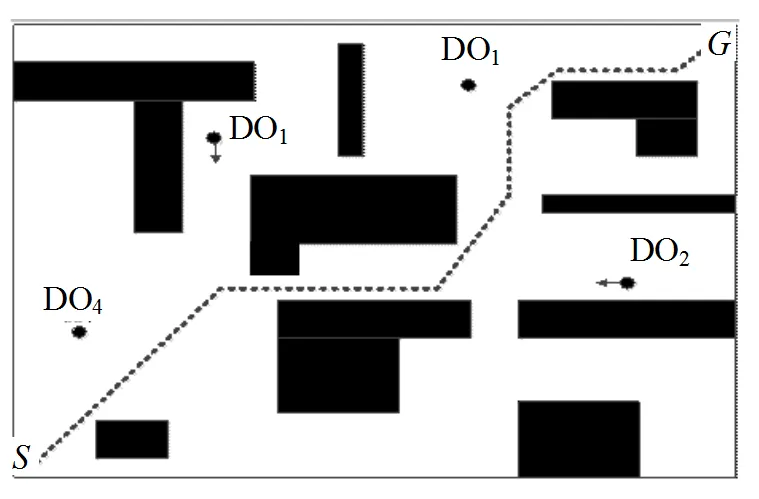
圖7 移動機器人環境空間及全局最優路徑

在2時刻，機器人到達位置。在當前滾動窗口內檢測到直線運動的動態障礙物。根據“直線運動障礙物預測避碰”方法，得出移動機器人與動態障礙物將在位置發生側碰。機器人通過在位置處停留時間，此過程如圖8b所示，如此則可避免與動態障礙物碰撞。

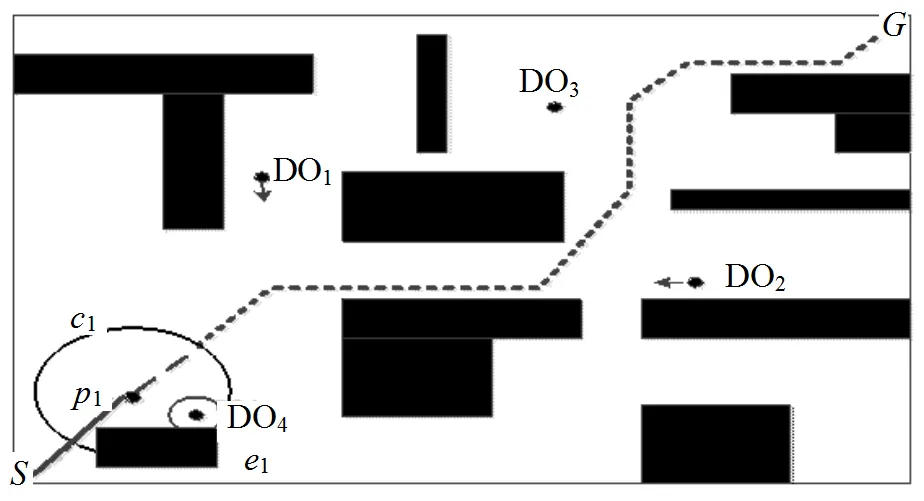
a. 動態障礙物方向不確定且無碰撞

b. 動態障礙物直線運動且發生側碰

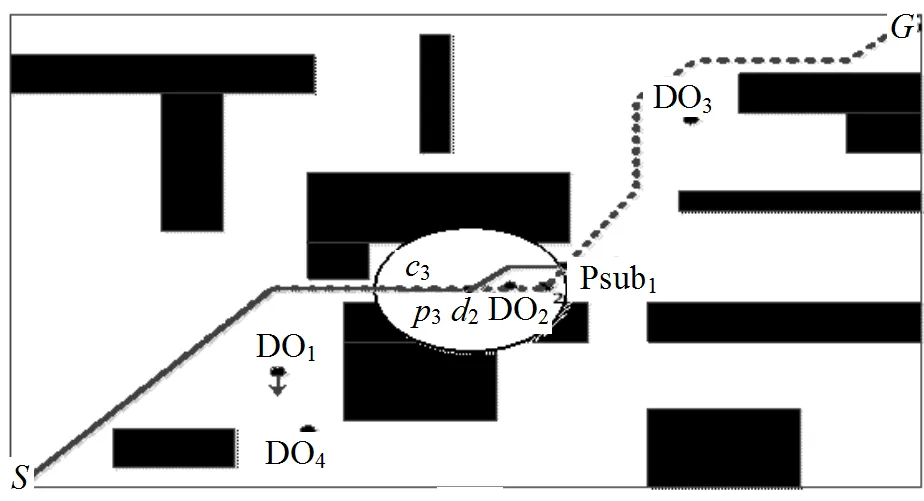
c. 動態障礙物直線運動且發生正碰

d. 動態障礙物方向不確定且發生碰撞

e. 初始路徑有障礙物停留

由實驗結果得，本文的避碰策略優于文獻[10]中的策略。如圖8d所示，當檢測到碰撞有可能發生時，策略一對動態障礙物進行膨化處理。此做法保守性很大，將大部分的可行區域都膨化成為了靜態障礙物。另外，這也常常引起在某些情況下，存在移動機器人無法規劃出可行路徑或者規劃出來的路徑較長的問題。在檢測到可能存在碰撞時，本文的策略二只對動態障礙物進行膨化處理，并減小移動機器人的步長，通過減小相應的膨化區域，從而進一步檢測碰撞是否發生。策略二的做法，可增加機器人的可行區域，從而能夠更高效地指導其進行路徑規劃。

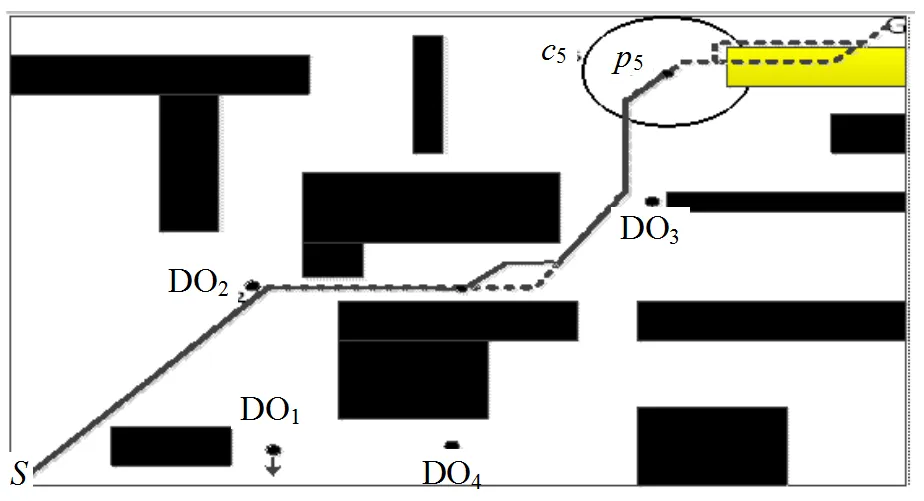
圖9中所示路徑即為本文所提改進蟻群算法指導移動機器人所獲得的無碰最優路徑。

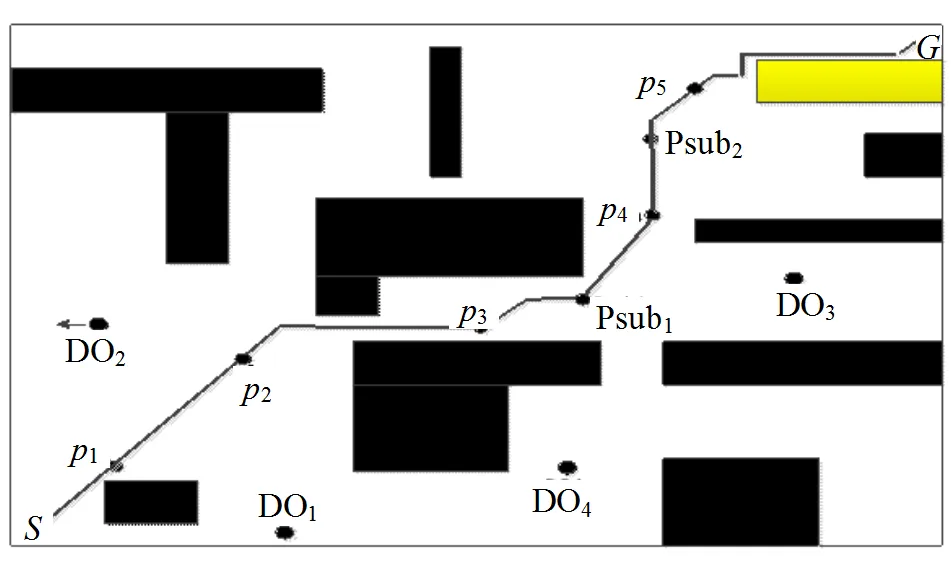
圖9 移動機器人最終的全局無碰路徑

6 結 論

本文研究了動態復雜環境下，基于環境先驗知識的單移動機器人路徑規劃問題，利用改進蟻群算法獲取全局路徑，并結合滾動窗口原理進行局部滾動預測避碰，最終獲取無碰最優路徑。本文考慮了動態障礙物直線運動和運動方向不確定的情況，給出了相應的碰撞避免策略，并針對不能適應環境變化的缺陷，加入Follow_wall行為。仿真實驗證明了本文算法的有效性，但是針對動態復雜情況下多移動機器人的路徑規劃問題，還有待于進一步的學習和研究。

[1] DORIGO M, MANIEZZO V, COLORNI A. Ant system: Optimization by a colony of cooperating agents[J]. IEEE Transactions on Systems, Man, and Cybernetics. Part B: Cybernetics, 1996, 26(1): 29-41.

[2] BAI J, YANG G K, CHEN Y W, et al. A model induced max-min ant colony optimization for asymmetric traveling salesman problem[J]. Applied Soft Computing, 2013, 13(3): 1365-1375.

[3] 任敬安, 涂亞慶. 基于蟻群優化的Ad hoc網絡路由協議實現[J]. 計算機工程, 2012, 38(11): 114-118

REN Jing-an, TU Ya-qing. Implementation of Ad hoc network routing protocol based on ant colony optimization[J]. Computer Engineering, 2012, 38(11): 114-118.

[4] 王欣盛, 馬良. 工件排序的改進蟻群算法優化[J]. 上海理工大學學報, 2011, 33(4): 362-366

WANG Xin-sheng, MA Liang. Improved ant colony optimization for scheduling problem[J]. Journal of University of Shanghai for Science and Technology, 2011, 33(4): 362-366

[5] ZENG Y, LIU D, HOU X. Complex vehicle scheduling optimization problem based on improved ant colony algorithm[C]//Proceedings of the 2012 International Conference on Information Technology and Software Engineering. Berlin: Springer, 2013: 805-812.

[6] CONSOLI P, COLLERA A, PAVONE M. Swarm intelligence heuristics for graph coloring problem[C]//IEEE Congress on Evolutionary Computation. [S.l.]: IEEE, 2013: 1909-1916.

[7] DENG X, ZHANG L, LUO L. An improved ant colony optimization applied in robot path planning problem[J]. Journal of Computers, 2013, 8(3): 585-593.

[8] TANG B W, ZHU Z X, FANG Q, et al. Path planning and replanning for intelligent robot based on improved ant colony algorithm[J]. Applied Mechanics and Materials, 2013, 390: 495-499.

[9] DONG S W, HUA F Y. Path planning of mobile robot in dynamic environments[C]//2nd International Conference on Intelligent Control and Information Processing (ICICIP). [S.l.]: IEEE, 2011, 2: 691-696.

[10] 王一可.基于滾動窗口的多機器人協調路徑規劃算法研究[D]. 上海: 上海交通大學, 2004.

WANG Yi-ke. A study of multi-robot cooperative path planning based on rolling windows[D]. Shanghai: Shanghai Jiaotong University, 2004.

編 輯 黃 莘

Research of Improved Ant Colony Based Robot Path Planning Under Dynamic Environment

QU Hong, HUANG Li-wei, and KE Xing

(Computing Intelligence Lab, University of Electronic Science and Technology of China Chengdu 611731)

This paper presents an improved ant colony algorithm for mobile robot path planning under dynamic complex conditions based on prior knowledge of global static environment. On the basis of conventional ant colony algorithm, by adjusting the transition probability, limiting the bounds of pheromone, and introducing relevant strategy to solve the deadlock problem, the improved ant colony algorithm not only can avoid the blindness of early planning and increase the diversity of solutions, but also can improve global search capability of the algorithm, and further reduce the possibility of algorithm prematurity as well. During the planning process, according to the direction changes of the dynamic obstacles, corresponding collision avoidance strategies are put forward. The Follw_wall behavior is introduced for unexpected situations in the environment. Simulation results show that the proposed algorithm is superior to conventional ant colony algorithm. It can effectively guide the mobile robot to avoid dynamic obstacles. Thus obtains a collision free optimal or suboptimal path, which adapts to the changes of the environment more effectively.

ant colony algorithm; dynamic complex environment; mobile robot; path planning

TP312

A

10.3969/j.issn.1001-0548.2015.02.017

2014-03-20;

2014-05-30

國家自然科學基金(61273308)；中央高校基本科研業務費(ZYGX2012J068)

屈鴻(1977-)，男，博士，副教授，主要從事機器學習、計算智能等方面的研究.