不同斜腔角驅動流的非結構網格研究

趙 楠，陳笑薇，丁 亮

（1.海軍駐上海地區艦艇設計研究軍事代表室，上海 201001； 2.中國船舶及海洋工程設計研究院，上海200011；3.上海船舶設備研究所，200031）

不同斜腔角驅動流的非結構網格研究

趙 楠1，陳笑薇2，丁 亮3

（1.海軍駐上海地區艦艇設計研究軍事代表室，上海 201001； 2.中國船舶及海洋工程設計研究院，上海200011；3.上海船舶設備研究所，200031）

在雷諾數100和1000兩種情況下，使用非結構網格技術對15°～165°斜腔驅動流問題進行了數值模擬。首先與已有的文獻結果進行了對比，當使用網格數為文獻 1/7網格數時，模擬結果與文獻符合的很好，表明非結構網格對于只能用非正交結構網格求解的問題有很大的優越性。然后對大斜角斜腔的驅動流場進行了預測。結果能為不同斜腔角的流場研究提供參考，并對工業類似結構的設計有一定的借鑒意義。

非結構網格；陣面推進法；SIMPLE算法；斜腔驅動流

0 引言

驅動流的數值研究在文獻中很常見，常被用于標準解來檢驗數值算法的穩定性、可靠性和高效性。其特點是幾何簡單，但包含基本的物理流動特征，在角區有反向旋轉的回流區。Burggraf[1]早在1966年就研究了方腔驅動流內的流場。Gupta等[2]于1981年使用半分析的方法給出了小雷諾數下尖角附近的驅動流與奇點問題，并與其他文獻的數值解進行了比較。 Ghia[3]使用了渦流函數法以及多重網格加速技術，在(129×129)網格數下對雷諾數 Re=1000的方腔驅動流給出了數值解。該文后來成為方腔驅動流較早的基準解之一，被大量后續研究者作為對比基準。Botella等[4]采用Chebyshev譜方法，Tezduyar[5]采用有限元法也分別給出了雷諾數下100和1000時的方腔驅動流內部流場。Stortkuhl等[6]首先用分析漸進解的方法給出了角區附近的流動解，然后使用多重網格法給出數值解，并指出隨著網格尺度的減小，數值解逐漸向漸進解靠近。Li等[7]使用高階的緊致四階有限差分格式，給出了雷諾數小于7500時的流場解。Tucker和Pan[8]沒有局限于數值算法，而是利用切割單元方法給出了驅動流流場解。Bruneau等[9]對兩維方腔驅動流進行了回顧并給出了Re=10000以內的基準解。相對方腔驅動流而言，由于斜腔驅動流內部網格劃分的不正交對數值算法提出了新的要求，對斜腔流的研究較少。Peric等[10]為了彌補非正交網格數值解法的不足，使用了較密的(160×160)和(320×320)兩種網格，分別給出了在斜腔角30o時Re=100和1000時的數值解，作者使用有限體積的SIMPLE算法求解結構網格內的N-S方程，并使用了多重網格加速技術。Oosterlee等[11]使用有限體積方法求解了一般曲線坐標下斜腔角30o和45o時定常不可壓縮N-S方程問題，給出了斜腔流動的數值解。

大部分對于斜腔驅動流的研究主要集中在斜腔角30o和 45o，且使用的都是結構化網格，很少使用非結構化網格的。非結構網格主要用于處理復雜外形、減小生成復雜網格生成時間上。由于易于網格自適應和采用動網格技術，在復雜幾何中得到廣泛應用[12]。事實上，受到設備內部流動空間的限制，斜腔驅動流在工業上應用十分廣泛，如斜船塢內流動，葉輪機械機匣處理的斜槽內流動以及軸承迷宮密封內的不穩定流動等。對于斜腔內流動問題的研究有助于了解這些復雜物理背景中的流場，對其內部的流場結構等情況加深認識，進而在結構設計階段給予建議，優化產品或結構設計，減少流動損失。

本文在張楚華[13]研究基礎上使用陣面推進法生成非結構網格，利用Laplacian算子和對角交換技術改善生成網格質量，對斜腔驅動流從斜腔角15o～165o范圍進行了N-S方程求解，給出了內部詳細流場，并與已有的標準解進行了比較。一方面驗證網格生成以及流場計算程序的可靠性，考核非結構網格用于簡單幾何問題的精度，另一方面給出各種斜腔角時的數值解，為以后不同斜腔角的流場研究提供參考，并對工業類似結構的設計予以借鑒意義。

1 陣面推進法

陣面推進法(Advancing front method)是最常見的非結構網格生成方法之一[14-16]，該方法的優點是不會引起物面穿透，邊界附近網格質量高。缺點是生成效率低，對背景網格的依賴性較強。其基本生成方法如圖1所示。首先輸入邊界離散點(如AB)，形成初始陣面，然后根據背景非結構化網格上所提供的局部尺寸參數，依據式(1)計算。

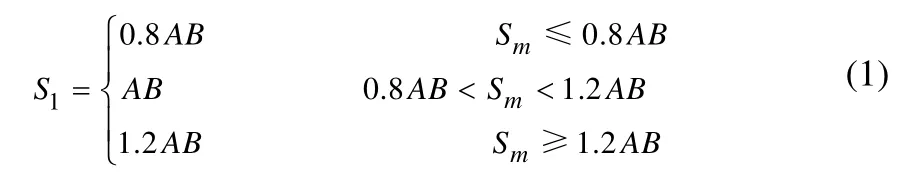
式中：Sm是AB中點尺度；S1是新生成點C離A、B點的距離。在陣面左側生成新的網格點(圖1中C點)，對該點及其某半徑r范圍內的點按式(2)、(3)進行篩選。

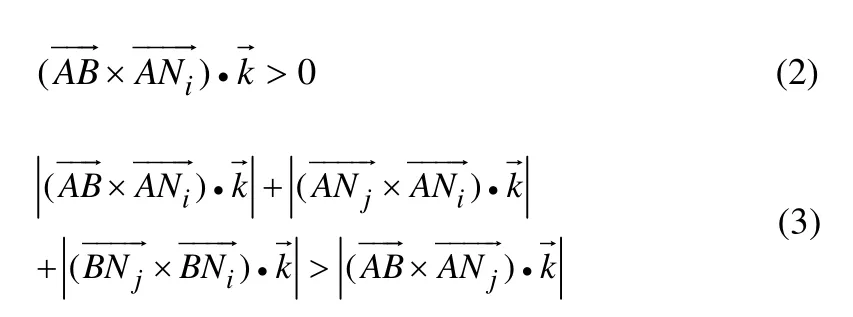
選取候選點序列(如Ni)，最后根據交叉判斷原則，剔除交叉點并選取最合適的點(圖1中D點)，形成新的三角形(如ABD)， 最后修改陣面，使邊界點的連接信息向流場內部推進，直至整個流動區域被三角形覆蓋為止。

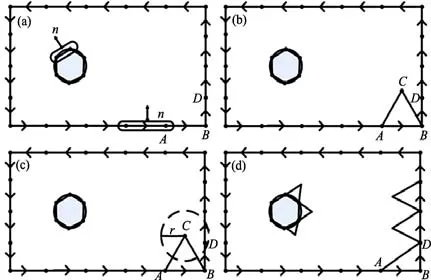
圖1 陣面推進法示意圖

使用上述算法生成的網格有時質量較差，會生成畸形網格，需要對其進行網格光順和對角交換。如圖2(a)所示，對角交換改變了網格的拓撲結構，實現了局部網格最小內角最大化的原則。而圖2(b)的網格光順則對網格單元的頂點幾何位置使用式(4)改進。

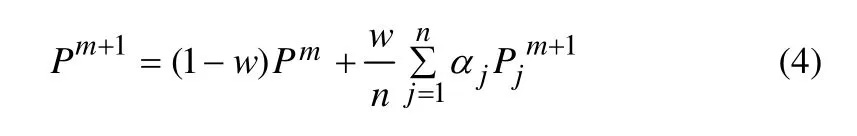
式中：Pj是待優化P節點的臨近點坐標，目的是將網格點盡可能地移到臨近網格點的中心。

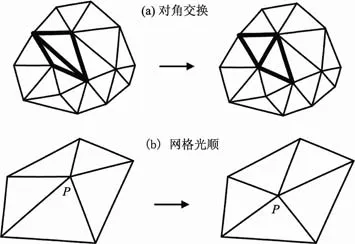
圖2 網格優化技術

2 數值公式

非結構化網格方法不需要進行坐標轉換，直接在原物理空間求解。在流動為定常不可壓縮的假設下，平面笛卡爾坐標系中的N-S方程可寫為通用形式：

式中：Φ為任一輸運量；ΓΦ為廣義擴散系數；為廣義源項；將控制方程(5)寫成積分形式：

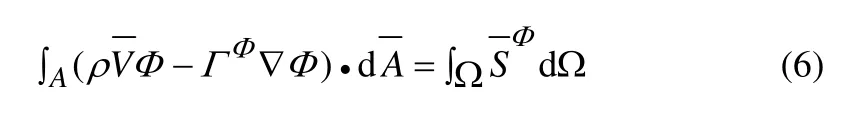
式中：ρ為密度；Ω為積分區域；A為Ω的邊界。直接采用三角形單元為有限控制容積，所有的求解變量Φ位于三角形的幾何中心，這樣對任意三角形單元，方程(6)可以離散為：

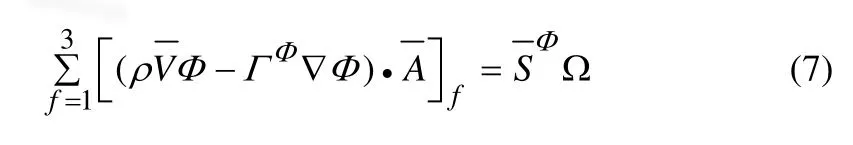
對方程(7)擴散項的離散要用到界面上的變量梯度，而對源項要用到中心點的梯度。界面上的梯度計算用圖3(a)所示的b-c-d-a積分曲線，假定界面梯度值為沿著積分曲線的平均值，可得：

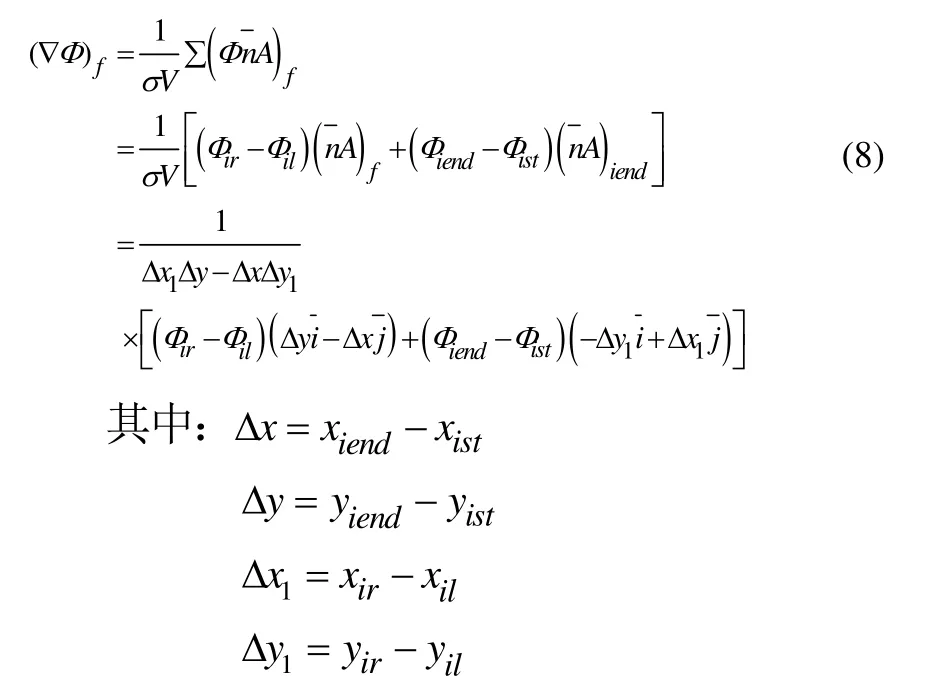
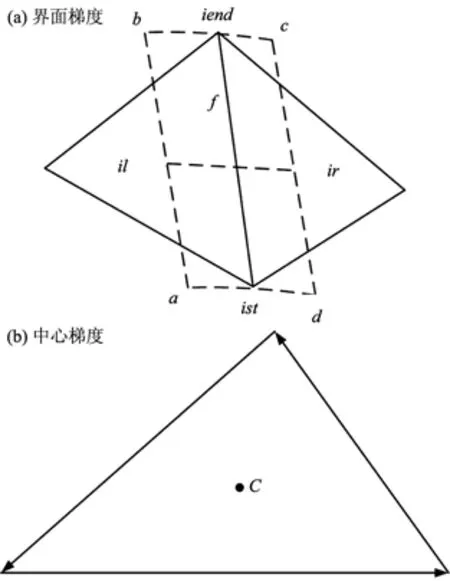
圖3 梯度計算積分曲線

對于單元中心的梯度，采用高斯定理重構，選取積分區域V為三角形單元C，并設單元中心處的梯度值為單元梯度的平均值：

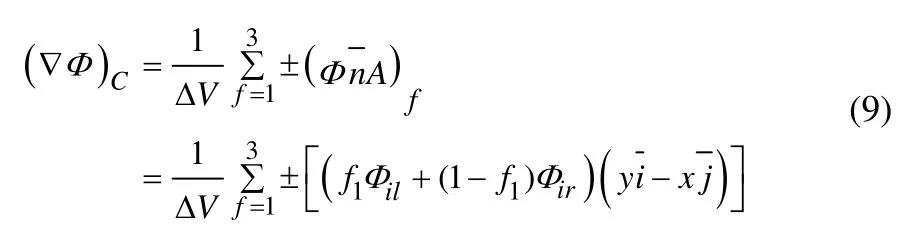
式中：f1為線性插值系數；ΔV為單元C的面積，當單元C為界面f的左單元時取正號，當單元C為界面f的右單元時取負號。

對于對流項中的界面變量值，使用二階精度混合差分格式，當Peclet數的絕對值小于2時采用中心差分格式，大于2時采用二階迎風格式：

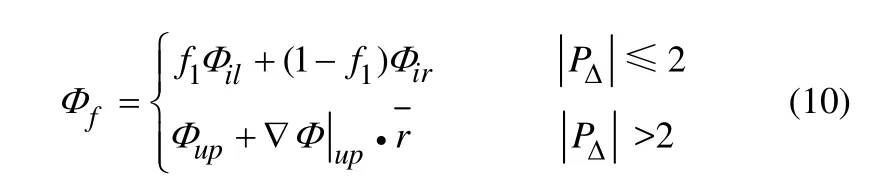
3 流場求解

采用推廣至非結構網格的同位網格Simple方法求解流場壓力分布，其基本步驟為：

1）預估步，對于假定的壓力分布P*，求解動量方程得到預估的速度U*、V*。

2）校正步，求解壓力和速度的校正值，使得校正后的壓力場和速度場同時滿足連續方程和動量方程。

為防止壓力場和速度場的失耦，將動量方程的壓力梯度項采用中心差分離散，但界面流速采用Rhie和Chow[17]提出的界面流速“壓力加權插值”式(11)計算。

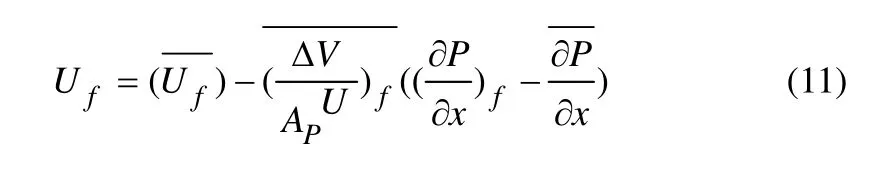
這樣相鄰點的壓力通過離散系數以及質量流量影響速度和壓力場，實現速度場和壓力場的關聯。將式(11)應用到非結構網格中，得到相應界面質量流表達式為：

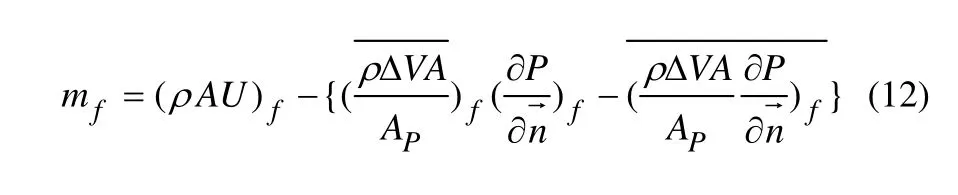
4 物理模型

二維斜腔驅動流物理問題的示意圖(見圖4)。AB、BC、CD為三個靜止固體壁面，而AD邊之外的流體以恒定速度UL沿著水平方向運動。無量綱雷諾數定義為Re=(ρULL)/μ，(μ為摩擦系數)。在 Re為100和 1000兩種情形使用陣面推進法生成非結構網格，對于斜腔角α從15o～165o進行了數值模擬，與已有文獻的結果進行對比，并給出了更廣范圍斜腔角的內部流場特征量。

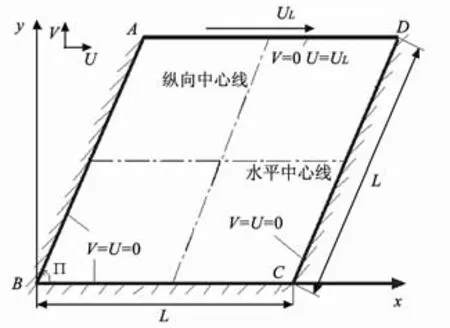
圖4 斜腔驅動流物理模型

5 數值結果

為驗證程序的正確性，首先將計算得到結果與文獻[18]、[9]給出的斜腔算例結果做了對比，雷諾數1000時斜腔角α=30o、45o的流線對比結果如圖5所示。

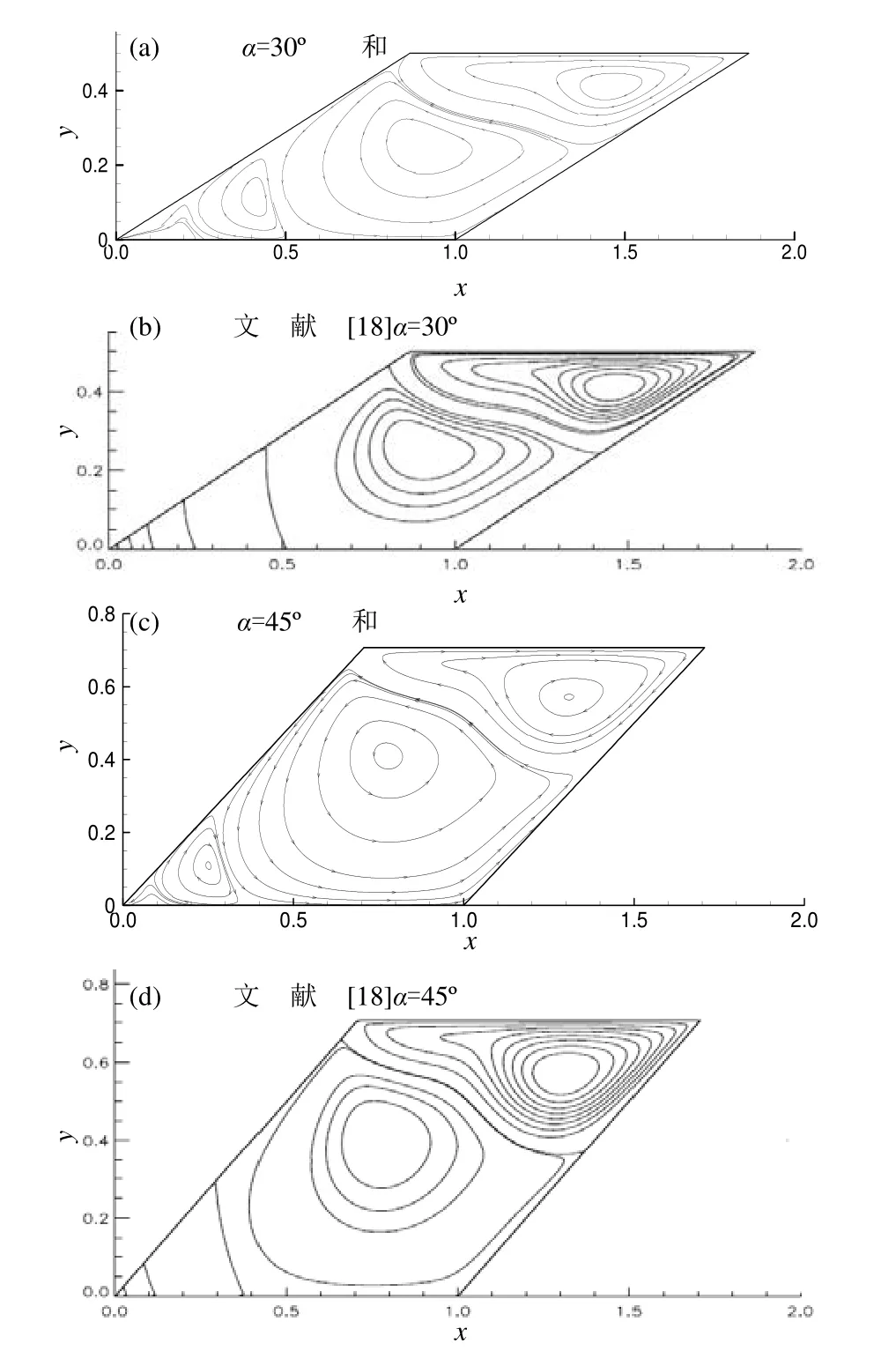
圖5 Re=1000時斜腔角30o和45o流線對比

很明顯，這兩個斜腔角時斜腔內流動結構主要由兩個大渦組成。本文計算得到的30o和45o兩種情況下，兩個大渦的分界線端點分別是(0.8，0.45)和(1.45，0.25)，(0.65，0.65)和(1.35，0.35)，這與文獻[18]符合的很好，但本文計算還在左下尖角處分辨出更小的渦結構。

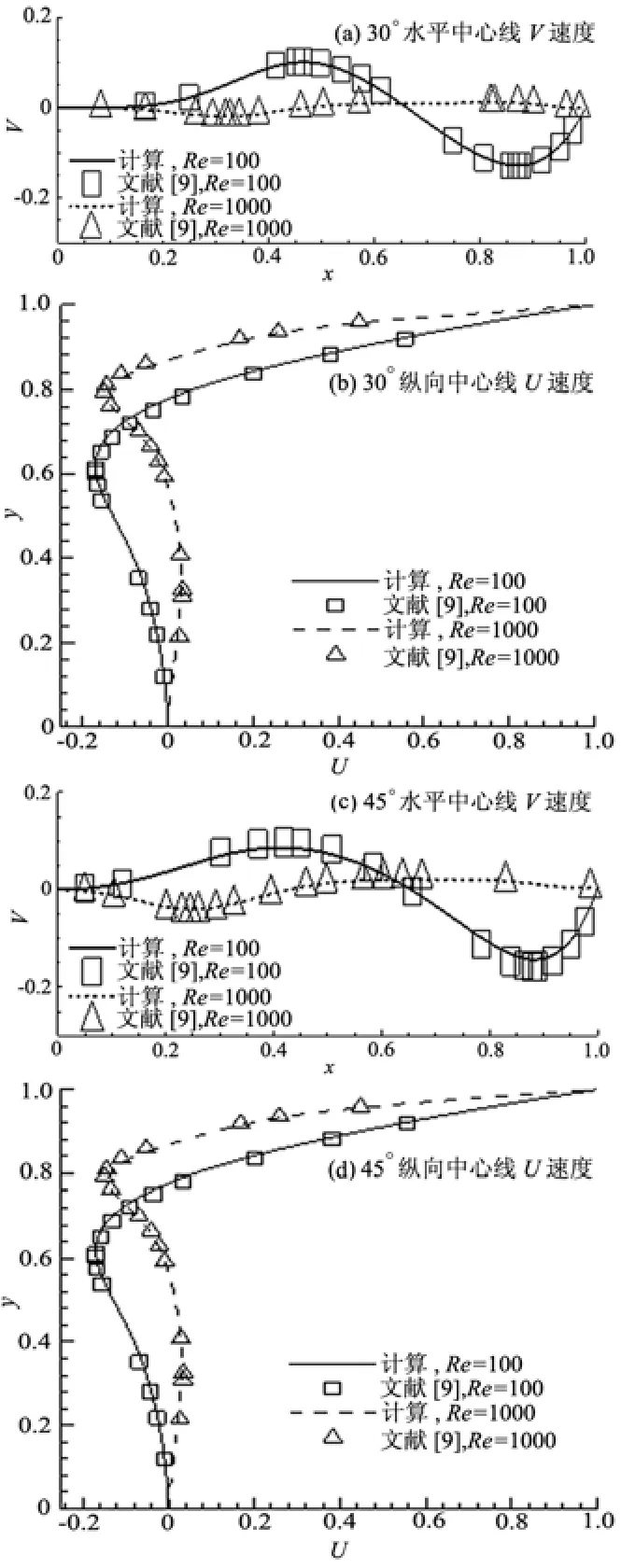
圖6 不同斜角的中心線速度分布對比

文獻[18]只給出了各物理量等值線的分布，沒有給出定量的數據。為了在定量上比較，又與文獻[9]中使用320×320的網格計算出的數值解結果做了對比。在Re分別是100和1000時，對30o斜腔和45o斜腔兩種情形水平中心線的V速度和縱向中心線處的U速度值共8條曲線進行了對比，結果如圖6所示。斜腔角45o時于x=0.404處達到V最大值0.082，x=0.879時達到V最小值-0.143。而在雷諾數為1000時，速度分布沿 x軸是先減小后增大再減小：斜腔角 30o時于x=0.31處達到V最小值-0.019，x=0.818時達到V最大值0.0174。斜腔角 45o時于x=0.253處達到V最小值-0.0398，x=0.6565時達到V最大值0.0212。速度的極值分布見表1。從圖6(b)、(d)的縱向中心線處的速度分布看出，雷諾數1000時無論是斜角30o還是45o，U速度均在y=0.9左右處衰減為0，并繼續減小，變為負值，到y=0.78處減小至負最小值；雷諾數100時U速度在y=0.75處衰減為0，并繼續減小，變為負值，到y=0.6左右處減小至負最小值。分析比較不同斜腔角度的速度線，再次證明了斜腔角度的影響相對于雷諾數而言是比較小的。表 2中給出了縱向中心線處的極值分布點。此外，文獻[9]中使用的是結構網格，本程序用的是非結構網格，總三角形單元數為16302個，相當于125×125的結構網格，其單元數是文獻[9]的 1/7。比較結果證明，二者計算精度完全相當，亦表明非結構網格對于只能用非正交結構網格求解的問題有很大的優越性，使用較少的網格即可以得到較準確的結果。

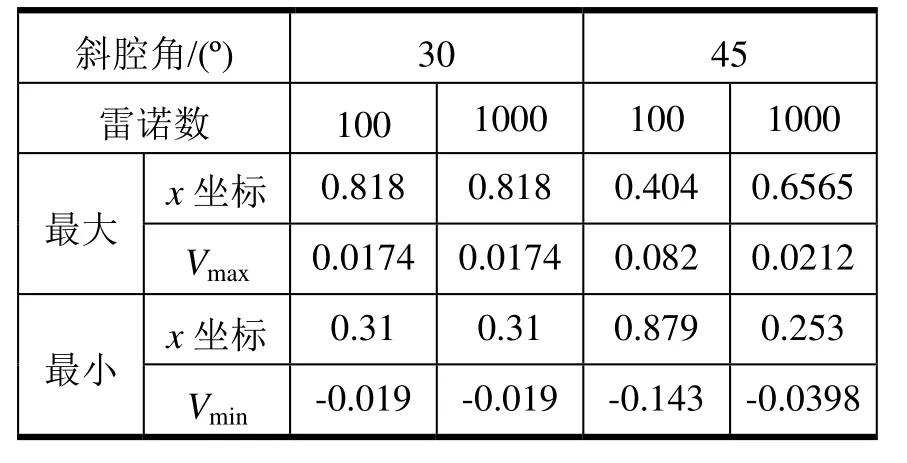
表1 水平中心線V速度極值點

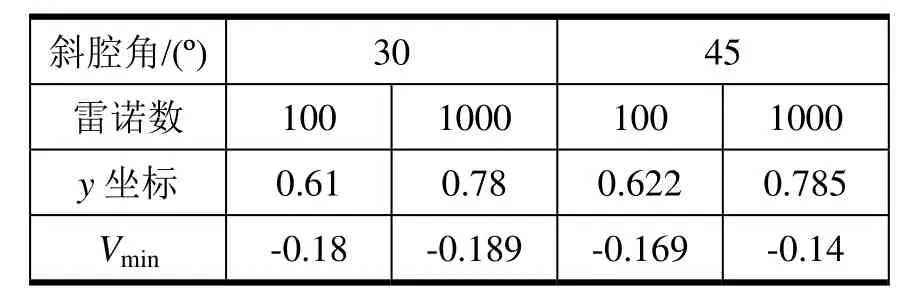
表2 縱向中心線U速度極值點

圖6(a)、(c)分別是斜角30o和45o斜腔水平中心線處的速度V沿著x軸的分布，圖6(b)、(d)是縱向中心線處的速度U沿著y軸的分布。實線─、虛線┈分別是雷諾數100和1000時的計算值，方形□和三角△分別是文獻[9]中雷諾數100和1000時的值。比較圖6(a)、(c)可以看出，不同的斜腔角度對速度大小有一定影響，但速度變化趨勢較類似。雷諾數為100時，速度V沿著x方向先增大后減小再增大：斜腔角30o時于x=0.465處達到V最大值0.1，x=0.869時達到V最小值-0.128。

進一步來說，若考慮到右上角主渦旋中心位置是流場中的主要特征量，與文獻[1，3，19-24]給出的90o方腔主渦旋坐標進行了比較，比較結果如表 3所示。文獻[24]給出了雷諾數100時的實驗結果，本文計算得到的雷諾數100時的結果與其符合的很好。

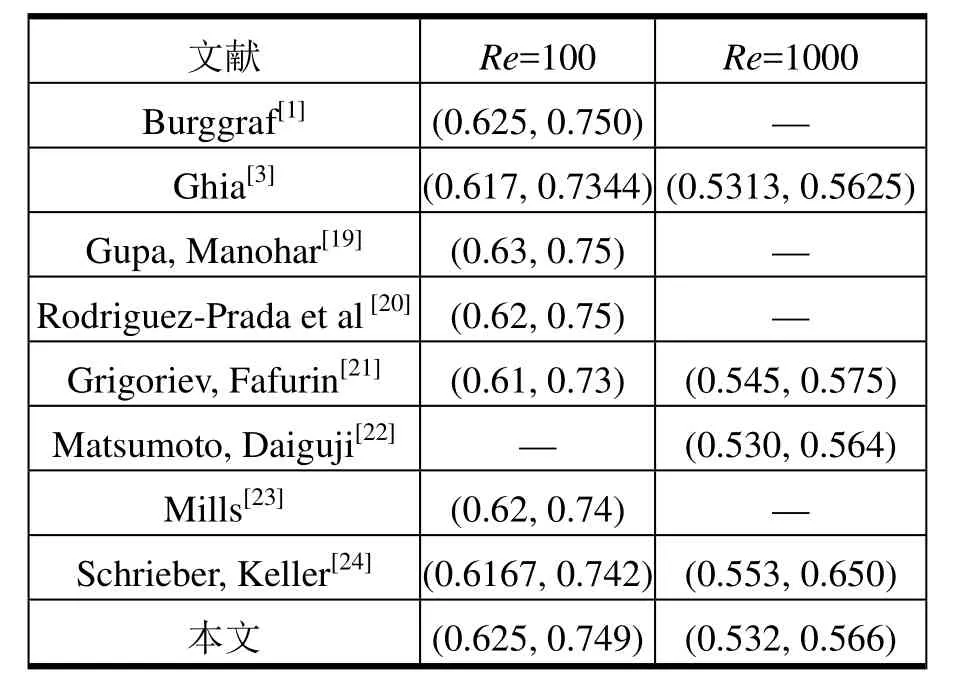
表3 主渦旋中心坐標比較

上文多角度的將本文計算結果與文獻中已有的結果進行了對比，充分證明了該計算結果的可信性，亦表明非結構網格在對于只能用非正交結構網格問題時有足夠的精度。圖7、8給出了雷諾數100和1000時計算得到的斜腔角15o至165o時內部流場的流線分布。

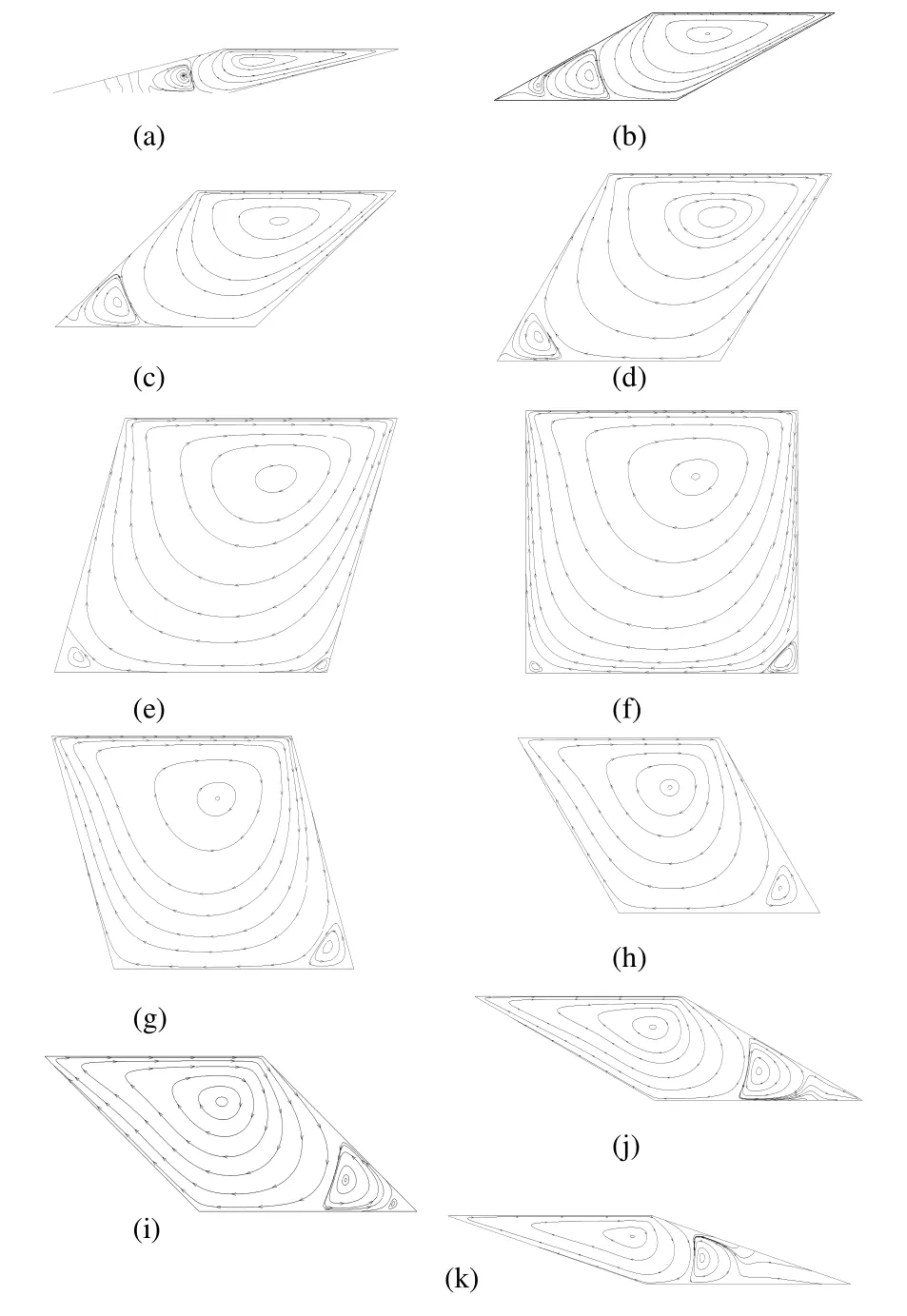
圖7 Re=100時15°～165°斜角的流線

圖8 Re=1000時15°～165°斜角的流線

表4給出了各個斜腔角時主渦旋的位置坐標。比較兩種雷諾數的主渦旋位置坐標發現，隨著雷諾數的增加，在水平方向上，當斜腔角位于 15°～60°時，主渦旋位置向右側偏移，而在75°～120°時，又向左側偏移，在135°～165°時再次向左側偏移；在垂直方向上，隨著雷諾數的增加，當斜腔角位于 15°～45°時，主渦旋位置向上部偏移，而在60°～165°時，主渦旋位置向下部移動。兩種雷諾數下，主渦旋的 x坐標都在斜腔角 30°時達到最大值，并隨著斜角的增加而變小。在Re=100時，主渦旋的y坐標在90°時取得極大值，而Re=1000時主渦旋的y坐標在60°取得最大值。

比較圖7、8的流線分布可以看出，隨著雷諾數的增加，流場特征變化最大的集中在斜腔角 30°～60°，在 Re=100時流場的渦結構主要由一個主渦構成，而Re=1000時是明顯的兩個大渦結構。在斜腔角處于120°～150°時，兩種流場主要差別集中在AB邊側。在Re=1000情況下的AB邊側能捕捉到明顯的渦結構，而Re=100時 AB側是較平滑的流線。對于斜腔角 15°和165°時，除了主渦位置外，兩種雷諾數下的流線并沒有顯示出明顯的性質區別。

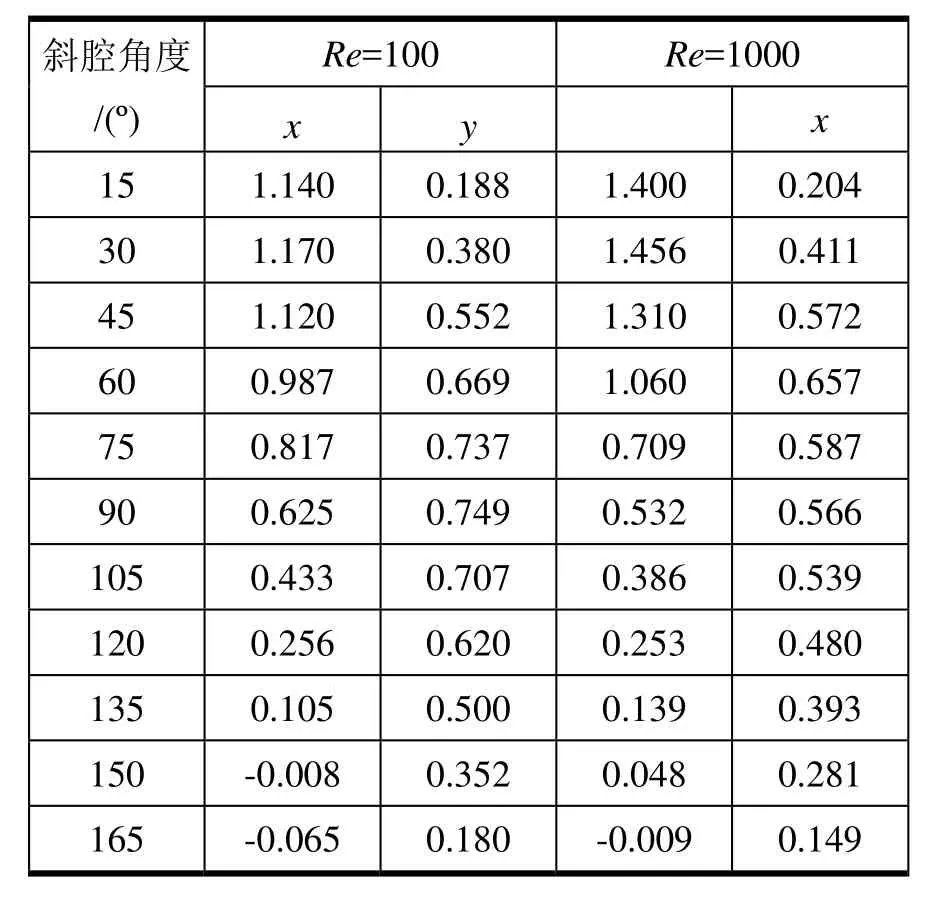
表4 不同斜腔角的主渦旋中心位置坐標

6 結論

本文利用非結構網格技術，對雷諾數100和1000時 15°～165°范圍斜腔角的驅動流問題進行了數值模擬，得到的結論如下：

1）首次采用非結構網格方法對不同斜角驅動流問題進行了研究。

2）本文計算結果與已有文獻結果比較表明，非結構網格對于那些只能用非正交結構網格求解的問題有很大的優越性，使用較少的網格即可得到可靠的結果。

3）斜腔驅動流中心線的速度受到雷諾數的影響比較大，速度分布會因雷諾數不同呈現性質上的變化；相對而言，斜腔角度只對速度值大小有一定影響，但不會影響速度分布趨勢。

[1]Burggraf O R.Analytical and numerical studies of the structure of steady separated flows[J].J.of Fluid Mech.,1966,24: 113-151.

[2]Gupta M M,Manohar R P,NOble B.Nature of viscous flows near sharp corners[J].Comput.Fluids 1981,9: 379-388.

[3]Ghia U,Ghia K N,Shin C T.High-Re solutions for incompressible flow using Navier-Stokes equations and a multigrid method[J].J.Comp.Phys,1982,48(3):387-411.

[4]Botella O,Peyret R.Benchmark spectral results on the lid-driven cavity flow[J].Comput.Fluids,1998,27(4): 421-433.

[5]Tezduyar T E.Stabilized finite element formulations for incompressible flow computations[J].Adv.Appl.Mech.,1992,28: 1-44.

[6]Stortkuhl T,Zenger C,Zimmer S.An asymptotic solution for the singularity at the angular point of the lid driven cavity[J].Int.J.Numer.Meth.Heat &Fluid Flow,1994,4,47-59.

[7]Li M,Tang T,Fornberg B.A compact fourth-order finite difference scheme for the steady incompressible Navier-Stokes equations[J].Int.J.Numer.Meth.Fluids,1995,20,1137-1151.

[8]Tucker P G,Pan Z.A cartesian cut cell method for incompressible viscous flow[J].Appl.Math.Mod.,2000,24: 591-606.

[9]Bruneau C H,Saad M.The 2D lid-driven cavity problem revisited [J].Comp.Fluids,2005,35(3):326-348.

[10]Demirdzic,Lilek Z,Peric M.Fluid flow and heat transfer test problems forNOn orthogonal grids:benchmark solutions[J].Int.J.Numer.Methods Fluids,1992,15(3): 329-354.

[11]Oosterlee C W,Wesseling P,Segal A.Benchmark solutions for the incompressible navier-stokes equations in general coordinate on staggered grids[J].Int.J.Numer.Methods Fluids,1993,17:301-321.

[12]Mavriplis D J.Unstructured grid technique[J].Annual Review of Fluid Mechanics,1997,29: 473-514.

[13]張楚華.三維湍流流動的非結構化網格數值解法及其在離心風機中的應用研究[D].西安: 西安交通大學,1998.

[14]L?hner R,Parikh P.Three-dimensional grid generation by the advancing front method[J].International Journal for Numerical Methods in Fluids,1988,8:1135-1149.

[15]Lohner R.Progress in grid generation via the advancing front technique[J].Engineering with Computers,1996,12:186-210.

[16]Thompson J F,Soni B K,Weatherill N P,et al.Handbook of grid generation[M].America: CRC Press,1998.

[17]Rhie C M,Chow W l.A numerical study of the turbulent flow past an isolated airfoil with trailing edge separation[J].AIAA J,1983,21: 1525-1534.

[18]Louaked M,Hanich L,Nguyen K D.An efficient finite difference technique for computing incompressible viscous flows[J].Int.J.Numer.Methods Fluids,1997,25(9): 1057-1082.

[19]Gupta M M,Manohar R P.Boundary approximations and accuracy in viscous flow computations[J].Journal of Computational Physics,1979,31: 265.

[20]Rodriguez-Prada H A,Pironti F F,Saez A E.Fundamental solutions of the streamfunction vorticity formulation of the Navier–Stokes equations[J].International Journal for Numerical Methods in Fluids,1990,10: 1-12.

[21]Grigoriev M M,Fafurin A V.A boundary element method for steady viscous fluid flow using penalty function formulation[J].International Journal for Numerical Methods in Fluids,1997,25: 907-929.

[22]Matumoto Y,Daiguji H.Convective-difference scheme using a general curvilinear coordinate grid for incompressible viscous flow problems[J].JSME International Journal Series II,1992,35: 4-9.

[23]Mills R D.Experimental investigation on cavity flows[J].Jourmal of Radar and Aeronautics 1965,69: 714.

[24]Schreiber R,Keller H B.Driven cavity flows by efficient numerical techniques[J].J.of Comp.Phys.,1983,49(2):310-333.

Study on Unstructured Grids of Inclined Cavity Driven Flow with Different Angles

ZHAO Nan1,CHEN Xiao-wei1,DING Liang3
(1.Navy Representative office at Warship Design and Research in Shanghai,Shanghai 201001,China; 2.Marine Design & Research Institute of China,Shanghai 201011,China; 3.Shanghai Marine Equipment Institute,Shanghai 200031,China)

The inclined cavity driven flow with inclined cavity angles of 15°-165° is numerically simulated by using unstructured grid method at Reynolds number of 100 and 1000.First,its results are compared with the existing literature results.When using the grid number is 1/7 grid number of reference literature,the simulation results are in good agreement with results of literature.It indicates that the unstructured grid has great advantage for problems that can only be solved withNOn-orthogonal structured grids.Then,the driven flow filed of inclined cavity with large angle is predicted.The results can provide a reference for flow field study of different inclined cavity angles and has the certain significance for the design of similar industrial structures.

unstructured grid; advancing front method; SIMPLE algorithm; inclined cavity driven flow

V211

A

10.16443/j.cnki.31-1420.2015.03.009

趙楠，男，工程師。輪機工程專業。