數形結合,讓算理與算法交融
王芳
算理和算法在計算教學中相輔相成,缺一不可。算理和算法又十分抽象,對于以直觀形象思維為主的小學生來說是學習的難點。數形結合思想是通過數與形的相互轉化,將抽象的數學語言與直觀的圖形結合起來解決問題的思想方法。有效運用數形結合的思想方法可以化抽象為直觀,幫助學生理解算理和掌握算法,提高計算教學效率。下面以“分數乘分數”一課為例談談具體的做法。
一、以形解數,感知算理
基于學生的生活經驗和思維,分數乘分數計算的算理和算法對于他們來說很抽象、難以理解的。所以,為分數找對應的圖形,以圖形來表達分數,解釋其中的算理,使學生在直觀操作中理解算理。
【片斷一】
1.探究1/2 ×1/4
師:像1/2 ×1/4 這樣的分數乘分數問題怎樣研究呢?如果用一個長方形表示“1”,那么怎樣畫圖表示出算式中的分數?請同學們試一試。
師:畫圖時先分了什么,表示了哪個分數?
生:先把單位“1”平均分成2份,取這樣的1份。
師:接著怎么分的?又取了幾份?
生:再把這一份平均分成4份,取其中的1份。
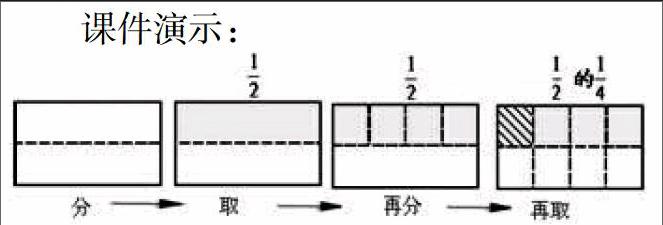
課件演示:
師:通過畫圖我們知道了1/2 ×1/4 實際上是求1/2 的1/4 是多少。那1/2 的1/4 到底是多少呢?是怎么知道的?
生:只要把剛才平均分的虛線畫下去,也就是把空白部分一起平均分,就能看出是1/8 。
師:8在哪里?1在哪里?
2.探究1/2 ×3/4
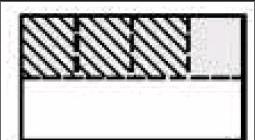
師:怎樣在長方形圖中表示出1/2×3/4?請大家畫畫看。
學生反饋:
師:1/2 的3/4 積是多少呢?怎樣修改這幅圖?
生:只要把整個大長方形豎著平均分成4份,整個大長方形一共平均分成了8份,所以1/2×3/4 =3/8 。
【教學分析】
在探究算理的過程中,以長方形作為探究材料。第一次讓學生嘗試畫圖,理清畫圖的方法,得出“分了取,再分再取”的畫法,“以形助數”,使學生理解1/2×1/4 = 1/8 是怎樣得到的;第二次畫圖則更注重以形解數,在追問中讓學生感知1/2×3/4 = 3/8 中3/8 的算理。兩次經歷從數到形,再從形抽象出數的過程,學生初步感知了算理。因此,在探究算理時,先教給學生準確的畫圖方法,再引導學生以形解數,層層遞進來感知算理。
二、以數思形,深化算理
畫圖操作初步理解算理后,常會發現學生很難用完整的數學語言對操作的結果加以提煉和概括,主要是因為學生由動手操作到抽象概括缺少了“表象”這一支撐點。兒童的認識規律,一般是從直接感知到表象,再到形成科學概念的過程,表象介于感知和形成科學概念之間,所以需要幫助學生建立這個支撐點,引導學生由具體思維合理地向抽象思維轉化,從而深化算理。
【教學分析】
在深化算理的環節中,教師讓學生靜靜地“想一想,先畫什么?再畫什么?”看似多余的一個過程卻非常有必要。因為“分數乘分數”算理模型的構建從具體思維向抽象思維轉化,對于學生來說是具有難度的,如果沒有留給學生一個思考的空間,沒有借助“在腦中畫圖”這種半具體半抽象的表象操作,那么一些學生難以實現從形象思維到抽象思維的有效轉化。
三、以數質形,向算法過渡
算理是算法的依據,它保證了計算的合理性和正確性;而算法是算理的概括,它為計算提供了快捷的操作方法。學生只有真正理解了算理和算法,才能靈活、準確地進行計算。因此,在對算理有了較深的理解后,要幫助學生從算理過渡到算法。
四、數形互釋,生成算法
算理和算法是計算教學中不可分割的兩個方面,只有實現算理和算法的相互交融,才能促進算法的有效生成。那么如何溝通“數”與“形”之間的聯系,促進算理和算法的交融,讓學生更進一步明晰“分母相乘、分子相乘”這一算理,從而有效生成算法呢?
【片斷二】
1.師:如果按照剛才的想法,3/5×4/7 怎樣計算?
生:5乘7作分母,3乘4作分子,積是12/35 。
師:我們利用長方形圖來驗證一下,該怎么分怎么取?
生:先把這個長方形橫著平均分成5份,取3份;再豎著平均分成7份,這樣一共平均分成了35份。
師:再取4份,最終取了多少份?
生:最終取了12份。所以3/5 ×4/7 的積是12/35
2.師:只驗證一題,還不能夠說明。換一題再試一試,行嗎?
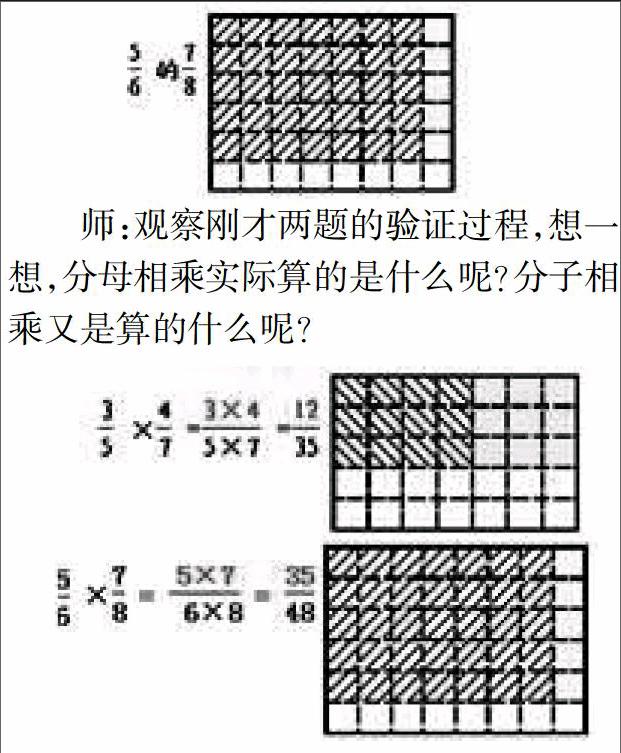
出示:5/6 ×7/8
師:從圖中你知道了什么?
生:6×8算的是把整個長方形一共平均分成了多少份,5×7算的是最終取了多少份。
師:觀察剛才兩題的驗證過程,想一想,分母相乘實際算的是什么呢?分子相乘又是算的什么呢?
生:分母相乘是求把單位“1”平均分成的份數,分子相乘就是取的份數。
師引導學生自主歸納出“分母相乘就一共分了多少份,分子相乘表示一共取了多少份”。
【教學分析】
上述教學中教師緊緊抓住引導學生驗證的過程,通過數形互釋,打通了算理和算法之間的聯系,有效促進算理和算法的相互交融。用“數解釋形” ,讓學生明白一共35份是指把整個長方形平均分成了5行7列,5×7就是35份;最終取了3×4=12份。由“形解釋數” ,使學生清晰了6×8算的是把整個長方形一共分成了48份,5×7算的是最終取的35份,從而自然得出“分數乘分數,分母相乘的積作分母,分子相乘的積作分子”的計算方法。學生再次經歷了自主驗證的過程,通過觀察、比較、驗證、歸納,在算法形成與鞏固的過程中進一步明晰算理,在真正理解算理的基礎上掌握算法,從而形成計算技能。再次利用圖形來溝通算理和算法的聯系,在數形互釋中進一步理解算理和掌握算法,使學生對計算方法做到知其然,更知其所以然。
在計算教學中,有的放矢地運用數形結合思想方法,為學生構建一個算理算法交融的課堂,引導學生在算法探究中理解算理,在理解算理的基礎上形成算法,那么計算課堂同樣會是精彩的。
【作者單位:太倉市城廂鎮第四小學 江蘇】

