從有形到無形的跨越

殷曉丹

工程問題在沉寂了幾年之后，人教版2014六上教材中再度呈現。我的理解是經過上一輪的教學實踐，教材編寫者和一線教師認識到工程問題對訓練學生的思維和培養學生的數學應用意識有著不可或缺的價值和意義，因此教材專門安排了一個工程例題的教學（42～43頁的例7）。

在工程問題教學中引導學生自我認識模型、自主建構模型、自覺運用模型，是課堂教學中教師必須跨越的，也是學生學習工程問題必須跨越的。

由此延伸，工程問題的建模過程也是學生從具體有形的實例解決到無形的數學思想領悟的跨越過程。

一、從整數到分數的跨越

1.由整數工程問題引入，幫助學生認識模型

學生最初是從整數來開始學習數學的，對整數有著天然的親近感和歸屬感，而整數的單一性（小數部分沒有計數單位）又給數據的處理帶來了方便。從這個意義上來說，創設整數的問題情境，有利于學生自我認識工程問題模型。

在例7教學之前，我設計了一道整數工程問題來鋪墊：

修一條長360米的路，一隊單獨修，12天能修完，二隊單獨修，18天才能修完。如果兩隊合修，多少天能修完？

鋪墊練習著重從兩個方面引導學生：一是引導學生自我認識工程問題的模型結構，具體地說就是有哪些數量，每個數量的含義是什么，哪些數量之間有關系，哪些數量之間沒有關聯；二是引導學生自我認識工程問題的數量關系。

由工作總量360米求兩隊合修的時間，學生自然聯想到要先求出兩隊合修的工作效率；由工作總量360米，一隊單獨完成時間12天，學生自然聯想到能求出一隊工作效率是每天修30米；由工作總量360米，二隊單獨完成時間18天，學生也能自然聯想到可求出二隊的工作效率。整數數量情境的創設調動了學生自我感知模型、自我認識模型的主動性和積極性。

2.由刪除工作總量遷移，引領學生探究模型

刪除“長360米”的條件，遷移至例7：

一條道路，如果一隊單獨修，12天能修完。如果二隊單獨修，18天才能修完。如果兩隊合修，多少天能修完？

學生最有可能想到的是假設路長，路長假設成多少呢？有講究，在運用不同的假設數據比較之后，孩子們會盡量假設成12米和18米的公倍數。但學生仍然沒有跳出“整數”圈，教師可適時點撥：①假設路長，不就是想先求出一隊、二隊的工效嗎！②沒有了具體的長度，我們也可以表示一隊、二隊的工效。③想一想什么數能幫忙？

三層點撥，三步臺階。第一層，明確假設路長的目的；第二層，達成這個目的還有第二條路；第三層，為第二條路指明方向。三步臺階之后，生成的是學生想到用單位“1”來表示工作總量，用分數表示工作效率。整數到分數的跨越是在沒有了具體工作總量的情況下“無意”中實現的，整數到分數的跨越也是工程問題學習從有形到無形的起點。

二、從具體到抽象的跨越

1.不同角度比較工程問題，助推學生由具體到抽象的跨越

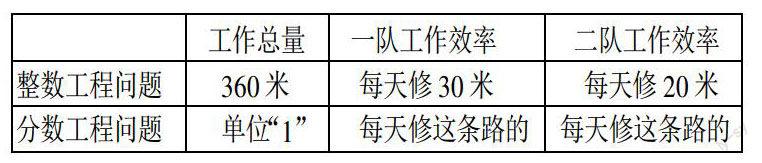
整數工程問題與分數工程問題本質上相同，都有工作總量、工作效率和工作時間，三者的相互關系也沒有改變，改變的只是它們的呈現形式。因此在學生嘗試解決了分數工程工程問題之后，我又送上一道“對比小菜單”：

引導學生由上至下對比同一列的數量，可以清晰地看到具體的數量與抽象的分率一一對應；從左往右橫向觀察各個數量，可以得出：如果工作總量假設成具體的數量（360米），那么相應的工作效率就可以是具體的數量。工作總量是工作效率的“因”，工作效率是工作總量的“果”，先因后果。因此把工作總量看做單位“1”，是學生自主探究工程問題的關鍵節點。

2.全面深刻理解分率本質，確保學生由具體到抽象的跨越

分率的本質是兩個數量之間的相對關系，具有高度的概括性和抽象性。譬如一隊工作效率，表示一隊每天的工作量占總工作量的，反映了一天的工作量與總工作量之間的相對關系；分率又內含了工作總量、工作時間的復合信息：工作總量為1，則工作時間為12天。

分數的本身就是一個概念模型，工程問題引入分數，高度濃縮了總量與部分量的抽象關系。深刻理解分數的意義，準確運用分數來表示工作效率，是從具體（量）跨越到抽象（率）的必由之路，是工程問題建模從有形跨越到無形過程中的關鍵一環，有著承上啟下的作用。

三、從變到不變的跨越

分數工程問題的探究始于假設工作總量，在多種假設可能性的對比中，引導學生觀察工作總量、工作效率、工作時間變與不變的現象，啟發學生思考分析工程問題中變與不變的實質緣由，升華學生對自主建構模型的認同感。

1.有層次地自主探究，生成變與不變的數據信息

教材編排為例題教學設置了三個層次：

層次一：假設路長18千米。

這個層次的探究還是停留在具體有形的數量上。

層次二：假設路長30千米。

當路長假設成30千米，求二隊工作效率，學生就“被逼”用到分數：

用分數數量來解決第二次的假設，或許是學生聯想到用分率來解決分數工程問題的“敲門磚”。

層次三：假設路長是1。

第三層的假設是在第一、第二層假設之后生成的。

三種假設得出數據，“變與不變”的探討順勢而生：

變：工作總量、工作效率。

不變：兩隊合修的時間。

2.有條理地拓展延伸，探討變與不變的實質緣由

“不同的方法計算出的結果一樣”，由此得出“不管假設這條道路有多長，答案都是相同的，把這條道路假設成1，很簡便。”如果學生的探究活動僅止于此，著實可惜。如果我們繼續引導學生想：

①路長變化，每天的工作量也隨之變化。

②但每天的工作量與路長的分率關系不變，也就是工效的分率不變。

③那么兩隊每天合修的長度占總長度的幾分之幾就是不變的。

……

通過逐層深入的交流探討，相信學生一定能悟出“合修時間不因工作總量的變化而變化”的實質緣由。延伸問題的思考探討，一定能將工程問題的模型牢牢地固化在孩子們的知識網絡之中，“變與不變”就跨越于無形之中。

工程問題再度“復出”，不是簡單地重復“昨天的故事”。新《課程標準》為我們工程問題教學指出了一條光明的坦途：引導學生自我認識模型、自主建構模型、自覺運用模型，做真正有用的數學！