在情境中感知在操作中理解
王金坤

【摘 要】 初學圖形與幾何時,要盡可能創設學生熟悉的、感興趣的實例作為認知背景,讓學生在情境中感知,為學生提供較為充分的觀察、操作、實驗、思考等數學活動的機會,讓學生在操作中理解。
【關鍵詞】 情境;感知;操作;理解
在一次“送教下鄉”活動中,我執教了蘇科版七年級下冊《6.4平行》一課。在多次研討交流的過程中,讓我感悟至深的是:初學圖形與幾何時,要盡可能創設學生熟悉的、感興趣的實例作為認知背景,讓學生在情境中感知,為學生提供較為充分的觀察、操作、實驗、思考等數學活動的機會,讓學生在操作中理解。下面,筆者結合《6.4平行》的教學流程,解讀教學設計的一些策略與意圖。
一、主要教學流程
1.情境創設
請同學們觀察右邊的四幅圖片,圖片中哪些線互相平行?
教室內有哪些線是互相平行的?它們有什么共同的特征?(小組討論,為歸納平行線的概念做準備)
2.認識平行
(1)概念:在同一平面內,不相交的兩條直線叫做平行線。
(2)表示:如圖,兩條直線互相平行,記作AB∥CD,讀作“直線AB平行于CD ”。
(3)畫法:想一想,小學里怎樣用直尺和三角尺畫平行線?
3.探究性質
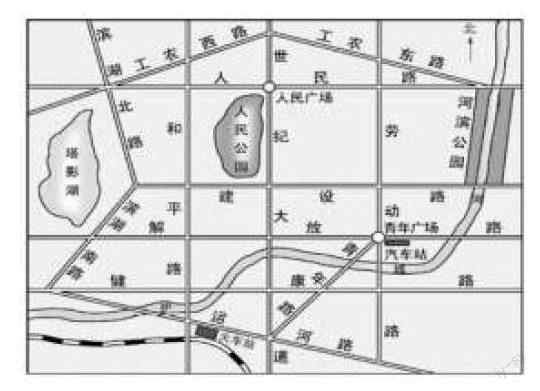
(1)讀圖。觀察地圖并思考:
①圖中有哪些道路與建設路平行?利用前面學習的方法加以檢驗;②過人民廣場,并與建設路平行的道路有幾條?經過青年廣場呢?③過人民廣場,能否再修一條與建設路平行的道路?經過青年廣場呢?
(2)畫圖。如圖,點A、B是直線l 外的兩點.①過點A畫與直線l平行的直線。這樣的直線能畫幾條?②經過點B呢?③通過畫圖,你有什么發現?
(3)歸納。學生思考、小組討論,嘗試用語言來描述所發現的基本事實:過直線外一點有且只有一條直線與這條直線平行。
(4)應用。如圖,D是AB的中點。
①過點D畫直線DE∥BC,交AC于點E,畫直線DF∥AC,交BC于點F;
②在所畫圖中,線段AE與EC、線段BF與FC有怎樣的數量關系?用刻度尺或圓規檢驗你的結論。
4.數學實驗
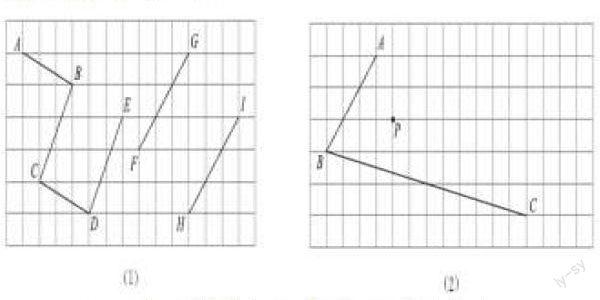
(1)圖中AB與CD、BC與ED、FG與HI互相平行嗎?
(2)在方格紙中過點P分別畫AB、BC的平行線。
二、設計策略與意圖
1.創設情境,讓學生在具體實例中感知平行。對于平行線的概念,小學里是通過實物、圖片加以描述的,未介紹平行線的表示方法,還學過利用直尺、三角尺畫一條直線的平行線。
基于小學已學過的平行的知識,這里我們通過一組圖片及尋找身邊的平行線,進一步豐富了對平行的認識,喚起了學生對平行的回憶。
2.遵循了從感性到理性,定義平行線
小學教材里是這樣描述的:像這樣不相交的兩條直線互相平行,其中一條直線叫另一條直線的平行線.本課的教學中,我們讓學生思考所找互相平行直線的共同特征,來歸納平行線的概念,遵循了從感性到理性的認知規律,深化了對兩條直線互相平行的認識。
3.在觀察、操作、思考等活動中探索平行線的性質
這一部分中有四個環節:第一,觀察城市地圖,在讀圖的過程中,讓學生從生活實際中感知平行線的性質;第二,將建設路看成直線l,人民廣場看成點A,青年廣場看成點B,這樣就轉化為一個畫圖問題,把上述實際問題抽象成數學問題,在操作中思考,讓學生從數學內部感知平行線的性質;第三,學生進行有條理的思考與表達,嘗試用規范的語言來描述所發現的基本事實;第四,運用平行線的性質解決問題,讓學生體會基本事實在數學內部的運用。
4.通過數學實驗,深化平行線性質的認識。這里的活動分為3個層次,第一,用直尺、三角尺畫平行線的方法檢驗圖中的有關直線是否互相平行:第二,通過觀察、操作活動,探索在方格紙中畫平行線的方法;第三,是數學實驗活動的核心,意在引導學生通過觀察、操作、思考,發現在方格紙中畫平行線的一般方法。
這樣的設計一方面基于學生在小學里已有的經驗(學過利用方格紙中的橫線或豎線畫平行線);另一方面,在檢驗圖中的直線是否平行的過程中觀察其特點,能引發學生新的思考,發現在方格紙中畫平行線的簡便方法,發現借助方格紙畫平行線的本質就是平移。
三、兩點感悟
1.創設恰當的情境有助于學生理解
數學。《課標》指出,應選用合適的學習素材,介紹知識的背景;設計必要的數學活動,讓學生通過觀察、實驗、猜測、推理、交流、反思等,感悟知識的形成和應用。恰當地讓學生經歷這樣的過程,對于他們理解數學知識與方法、形成良好的數學思維習慣和應用意識,提高解決問題的能力有著重要的作用。
對于七年級學生來說,學生對圖形的認識僅僅限于直觀性的識圖,以前沒有學習圖形的表示方法、幾何語言的表述和推理,所以從實際情境中抽象出圖形、概念、性質,并用幾何語言加以表述,是比較困難的。因此,教學中要以現實背景為素材創設情境,讓學生經歷觀察、操作、思考、推理等活動過程,積累數學思維和實踐活動的經驗,讓學生親身實踐、感受,掌握概念、懂得畫法、嘗試用幾何語言表述,有助于學生理解數學,這是有效的學習方法。
2.立足合情推理,發展學生有條理的思考與表達。合情推理是發現結論的一個有效途徑。記得華東師大王繼延教授說過,培養學生在活動中從數學的角度進行思考,直觀地、合情地獲得一些結果,這是數學的根本,是得到新結果的主要途徑。
七年級的學生習慣于用小學里的直觀來代替推理,對幾何語言的運用,對文字語言、圖形語言、符號語言的相互轉化,對探索、歸納、推理的必要性認識不足.因此,教學中,我們應引導學生觀察、操作、實驗,其目的是為了獲得抽象的規律,發展空間想象力和推理能力。學生的認識過程應當是基于操作,又高于操作,經過抽象、概括活動,歸納數學對象的特征,發展有條理的思考與表達。

