基于改進帝國競爭算法的微網動態經濟調度

翟云峰，易國偉，王 亦，李 明，周 鵬

（長沙理工大學電氣與信息工程學院，湖南長沙410004）

基于改進帝國競爭算法的微網動態經濟調度

翟云峰，易國偉，王 亦，李 明，周 鵬

（長沙理工大學電氣與信息工程學院，湖南長沙410004）

微網并網模式下，針對微網中光伏、風電及負荷等不確定因素的影響，在滿足系統各個約束條件下，建立了基于機會約束規劃的微網動態經濟調度模型。模型以微網總的運行成本最小為目標，綜合考慮了可控機組燃料成本、CO2排放治理成本、機組維護成本，低壓配電網有功購買成本和旋轉備用購買成本等。采用概率約束形式刻畫了微網系統運行的可靠性，并考慮了可控機組的出力約束及爬坡約束。針對帝國競爭算法存在收斂速度慢和易陷入局部最優的問題，通過引入混沌原理和隨機模擬技術，提出改進帝國競爭算法求解所建數學模型。最后，以一個微網系統為例，分析不同可靠性水平對系統經濟性和調度結果的影響，同時比較了所提算法和常規算法收斂特性，驗證了所提算法的有效性。

微網；機會約束規劃；動態經濟調度；帝國競爭算法；混沌映射

0 引言

近年來，由于環境問題和能源問題日益嚴重，分布式能源因其具有節能、環保的特點，逐漸受到人們重視。但是，由于分布式發電具有間歇性和不可控性的特點，導致其難以接入電網。而微網靈活、系統的將分布式電源和本地負荷組成了一個整體，它的出現為分布式電源接入電網提供了一個很好的途徑，既可以使分布式能源得到充分利用，同時減輕了分布式能源接入電網所引起的沖擊［1，2］。

微網經濟調度分為為微網靜態經濟調度和微網動態經濟調度，其中微網動態經濟調度考慮了各個時段的耦合性，較單研究一個時段上的靜態經濟調度更符合現實情況。目前國內外已有不少關于微網經濟調度方面的研究。文獻［3］針對微網并網模式下的優化調度問題，建立了考慮發電成本、污染物排放成本的多目標微網優化調度模型，并采用改進多目標粒子群算法對模型進行求解，仿真結果表明該算法能使所有目標達到最優。文獻［4］針對微網并網和孤島兩種運行方式下的經濟調度問題，考慮分時電價和與配電網交易，以最小化發電成本為目標，建立了2種運行方式下的經濟調度模型。但文獻［3，4］均未考慮機組爬坡約束和微網系統運行的可靠性。文獻［5］對微網并網運行方式下的微網動態經濟調度進行了研究，建立了優化微網內分布式電源出力和配電網向微網輸入功率的數學模型，并采用加入自適應措施的粒子群算法對模型進行求解，但并未考慮風電和光伏等不確定因素對微網的影響以及微網系統運行的可靠性。

微網動態經濟調度問題是一個非凸、非線性、非光滑的復雜問題，傳統的算法難以完成其求解，目前常用的智能算法有:粒子群算法（PSO）、遺傳算法（GA）、蟻群算法（ACO）等，各有利弊，尋找適合求解微網動態經濟調度問題的優化算法是解決該問題的難點之一。帝國競爭算法（imperialist competitive algorithm，ICA）［6］是由Atashpaz-Gargari等人于2007年首次提出，能夠很好地解決優化問題。該算法原理源于人類政治社會中帝國之間相互爭奪殖民地的過程［7］，相比于PSO算法，ICA算法在解決經濟調度問題上有明顯的優勢［8］。文獻［9］表明ICA算法相比于GA算法具有更好的連貫性和收斂精度，但是，基本帝國競爭算法仍存在收斂速度慢，易陷入局部最優的問題，需要進一步對其改進。

基于以上研究，本文以微網總的運行成本最小為目標，考慮了機組燃料成本、機組維護成本與CO2排放治理成本和旋轉備用成本等，建立了基于機會約束規劃的數學模型。考慮到風電、光伏以及負荷的波動性，采用從配電網購買旋轉備用的形式來平抑波動；并考慮現實情況下旋轉備用并非時刻滿足運行要求，因此這里旋轉備用采用概率水平的形式滿足系統運行要求。之后采用帝國競爭算法對模型進行求解，并結合隨機模擬技術及混沌原理對帝國競爭算法進行了有效改進，提出了基于改進帝國競爭算法的微網動態經濟調度優化方法。

1 微網系統中的不確定性因素

1.1 負荷的不確定性

負荷預測誤差δt，L一般服從正態分布，即δt，L～N（0，）［10，11］。算例分析時，可由此隨機產生各時段負荷隨機數。

1.2 風電的不確定性

風機出力和風速有關［12～15］，而風速服從威布爾分布［16］，其概率密度函數為:

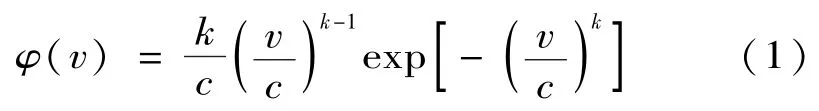
式中:k是形狀參數；c是尺度參數；v是實際風速。

風電機組輸出功率PWT與風速v間存在下面分段函數關系［17，18］:

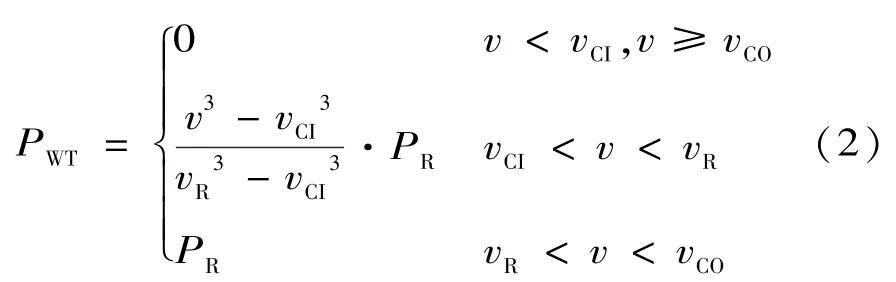
式中:vCI；PR；vCO；vR分別是風電機組的切入風速、額定功率、切出風速、額定風速。

算例分析時，先利用HOMER軟件［19］產生隨機風速，然后利用式（2）產生各時段風電機組輸出功率的隨機數。

1.3 光伏發電的不確定性

太陽的光照強度近似服從Beta分布［11］。其概率密度函數為:

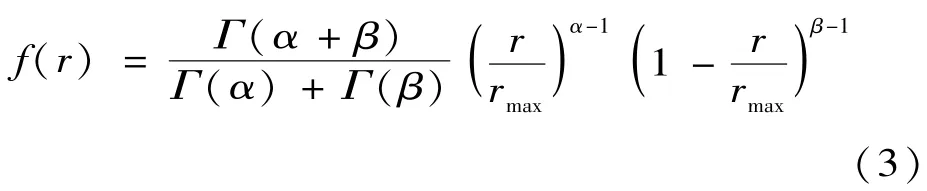
式中:r和rmax分別為實際光照強度和最大光照強度；α、β為Beta分布的形狀參數。

Beta分布的形狀參數可根據光強平均值μ′和標準差σ′近似計算出來，其公式為:

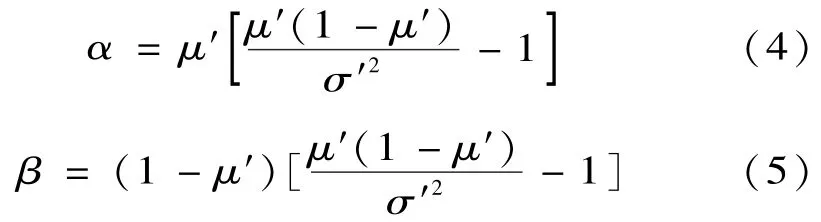
光伏出力PPV與光照強度r有如下關系:

式中:A為光伏方陣面積；η為光伏方陣光電轉換效率。

由光照強度的概率密度函數，通過式（6）可得到光伏出力的概率密度函數fPV也服從Beta分布:

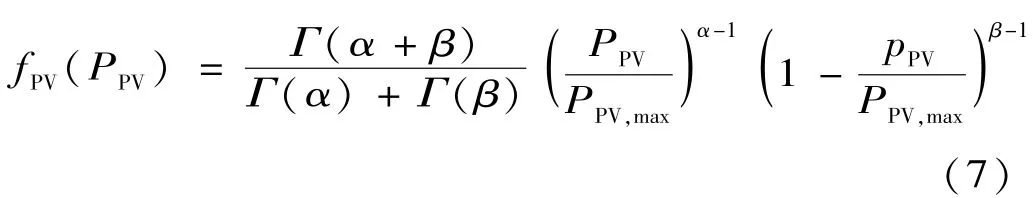
式中:PPV，max=Aηrmax為光伏出力最大值。

數值分析時，利用HOMER軟件產生24h光照強度值，然后由式（4）和（5）計算得24時段Beta分布參數α和β，再由隨機模擬方法產生各時段光伏出力值。

2 微網動態經濟調度的數學模型

2.1 目標函數

微網動態經濟調度目標是在滿足系統各個約束條件下，優化各優化變量的取值，使得在調度期間內微網系統內的運行成本最小。因此目標函數為:

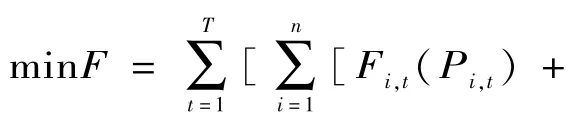
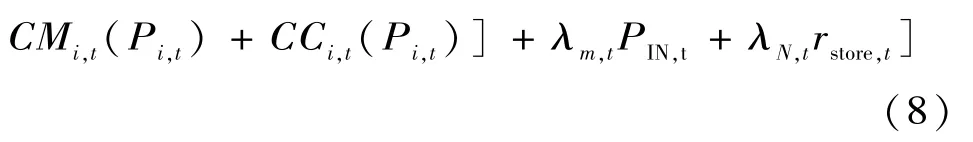
式中:F為調度周期內的系統運行成本；Fi，t（Pi，t）為可控機組的燃料成本；CMi，t（Pi，t）為可控機組的維護成本；CCi，t（Pi，t）為可控機組的CO2排放治理成本；Pi，t為可控機組i在時段t的調度出力；PIN，t為時段t微網從低壓配電網（distribution network，DN）購買的有功功率；λm，t為t時段的電價；rstore，t為t時段從DN購買的旋轉備用；λN，t為t時段從DN購買旋轉備用的價格；n為微網系統可控機組的數量；T為一個調度周期內所含有的時段總數。可控機組是指輸出功率可以控制的機組，反之則為不可控機組。本文所考慮的可控機組為微型燃氣輪機（micro turbine，MT）和柴油機（diesel generator，DE），不可控機組為風機（wind turbine，WT）和光伏電池（photovoltaic cell，PV），其中不可控機組直接工作在最大功率跟蹤模式。DE，MT，DN和DN備用為本文微網動態經濟調度主要優化控制對象。

針對上面的成本函數，下面分別表示為:

（1）燃料成本函數［20］:

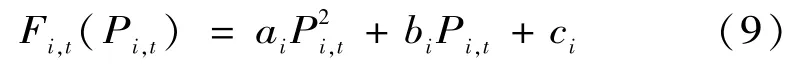
式中:ai，bi和ci為燃料成本系數；Pi，t是機組i在t時段的輸出功率。

（2）維護成本函數［21，22］:

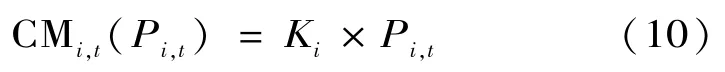
式中:Ki為可控機組i維護成本系數。

（3）CO2排放治理成本函數［23］:

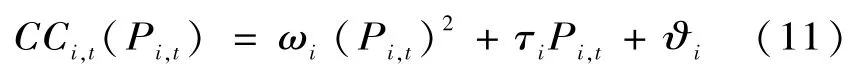
式中:ωi，τi，?i分別為可控機組i的CO2排放治理成本系數。

2.2 約束條件

（1）功率平衡約束:

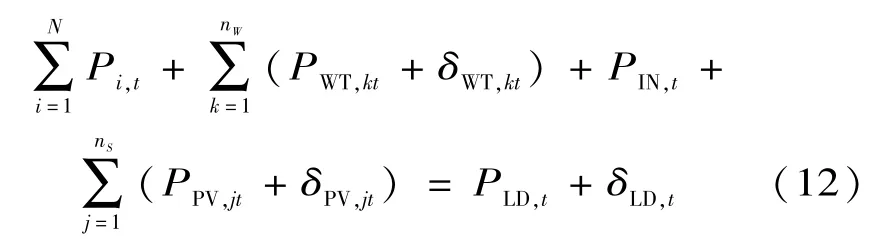
式中:δWT，kt，δPV，jt和δLD，t分別是風機k、光伏電池j和負荷在時段t的波動誤差；PWT，kt，PPV，jt分別為風機k和光伏電池j在時段t的出力預測值。

（2）可控機組的出力約束:

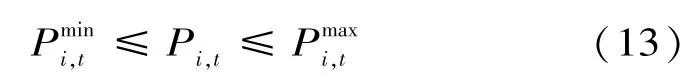
式中:Pi為分布式電源i的輸出功率；，為其上下限。

（3）可控機組爬坡約束:

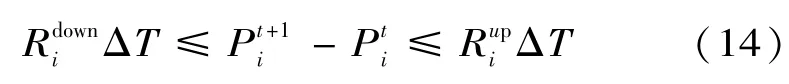
（4）旋轉備用約束:

由于在微網運行期間，存在著負荷、風電和光伏等不確定因素，如果要使所有運行情況下旋轉備用均滿足系統要求，那么所需的旋轉備用成本會十分巨大。而在實際系統運行中，并非時時刻刻都滿足系統可靠性要求，在此本文給定概率水平β，并定義β為微網可靠性評估指標，β越大微網可靠性越高，將旋轉備用以概率形式刻畫:

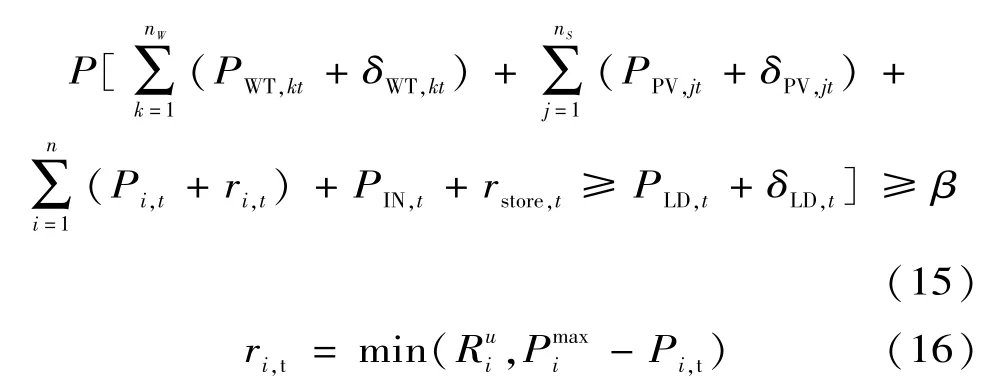
式中:ri，t為時段t可控機組i所能給出的旋轉備用容量，取決于可控機組最大輸出功率、當前輸出功率和機組爬坡能力；β為事先給定的概率水平。

3 基于隨機模擬的改進帝國競爭算法

3.1 隨機模擬技術

隨機模擬，又被稱為Monte Carlo模擬，通常用在隨機系統抽樣測試，它以根據給定的概率抽取隨機變量為基礎。隨機模擬技術給出的結果并非精確的結果，而是統計結果，但對于諸如機會約束規劃模型這樣的問題，其可能為唯一的有效方法。

對于機會約束:

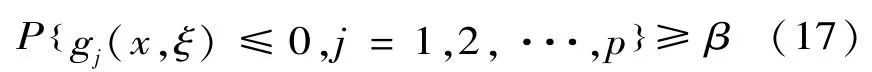
式中:ξ為一個已知概率密度函數為φ（ξ）的隨機向量；x為決策變量。

檢驗約束條件是否滿足的過程如圖1所示。

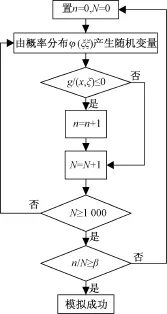
圖1 隨機模擬技術檢驗約束條件過程

3.2 基本帝國競爭算法

帝國競爭算法（ICA）是進化競爭領域內一種新的進化算法，是以人類的政治社會演變過程中帝國之間相互爭奪殖民地現象為基礎的。算法由N個初始國家開始，它們中Nimp個最強大的國家被選中作為帝國，剩下的國家是殖民地。每一個殖民地都屬于某一個帝國。在算法運行的過程中，表現為帝國之間相互爭奪殖民地，力量強大的帝國有更大的可能性占領更多的殖民地，而力量弱小的帝國則有更大的可能失去殖民地。當所有的殖民地被某一帝國占領，則算法結束。該算法分為以下5個階段:

（1）帝國初始化。待求的h個決策變量構成的一個h維向量代表一個國家cot=［x1，x2，…，xh］。設國家總數為Ncot，其中帝國數為Nimp，殖民地數為Ncol（Ncol+Nimp=Ncot）。每個國家的成本值即目標函數為f。定義第n個國家標準化之后的能量值為:

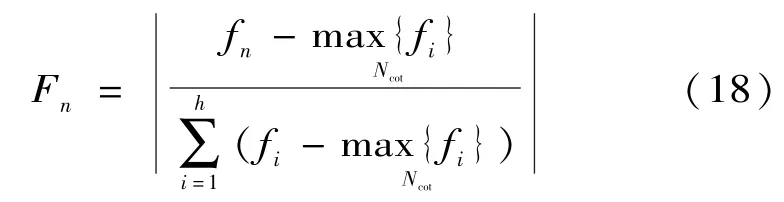
式中:i為第i個國家。對于最小化問題，成本越小即能量越大。

（2）殖民地同化。當一個帝國侵占一個殖民地后，殖民地由于被帝國影響而向帝國靠近。移動的距離l～U（0，δ×d），d為帝國距離殖民地的長度，δ＞1，即可保證殖民地能從各個方向靠近帝國；移動方向和殖民地與帝國連線的夾角θ～U（-γ，γ），γ為偏移量調整參數。

（3）帝國更新。當帝國所占領的殖民地能量值大于帝國時，帝國要與該殖民地位互換，即該殖民地升級為帝國，帝國降級為殖民地。

（4）殖民競爭。殖民競爭要首先計算每個帝國的總能量值，定義標準化之后的帝國k的總能量值為:

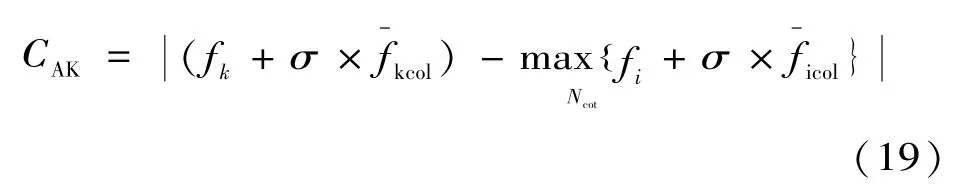
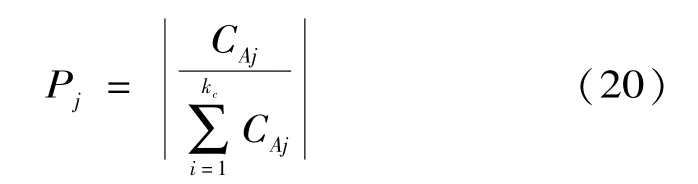
（5）刪除帝國。經過帝國競爭之后，能量值較小的帝國的殖民地會被能量值大的帝國所占領，最終會失去所有殖民地，此時該帝國即為滅亡，在算法中的位置也會被消除。當算法中只有一個帝國的時候，所有殖民地即被該帝國占領，該帝國即為最優解，算法迭代結束。否則，返回階段（2）。

3.3 混沌原理

混沌運動是一種既有規律性由又具有不可預測性的運動，有確定的方程描述，但在某一時刻的運動狀態又是未知的，即混沌運動在空間中的運動軌道是隨機的。混沌映射對解決優化問題是非常重要的，具有對初始條件非常敏感、遍歷性等特點。由于ICA算法有易陷入局部最優的缺點，混沌理論被引入以克服易陷入局部最優的缺點，并加快其收斂速度。

3.4 ICA算法的改進

一維不可逆轉映射是最簡單的能產生混沌運動的系統。Logistic map是著名的混沌映射，最早由Robert May提出［24］映射公式如下:

式中:c是控制參數，用以保證混沌運動。如果使yk=（xk+1）/2并令c=4，那么（21）式變成了xk+1=1-2（xk）2。假設r為控制參數，logistic map變為式（22）:

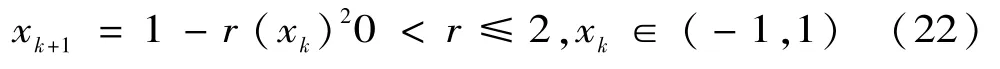
本文采用一維混沌映射。（24）和（25）表示了前一代和后一代變量之間的關系，以及初始參數的取值。

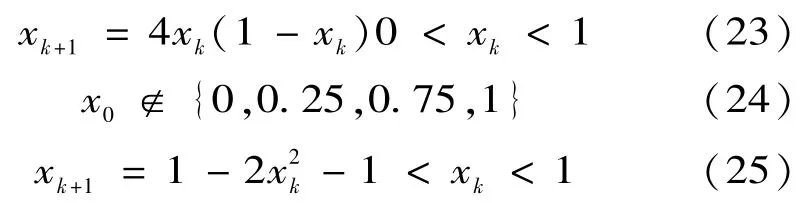
鑒于ICA算法易陷入局部最優，為了加強全局搜索能力，把混沌映射引入到ICA算法中。θ是殖民地同化過程中殖民地移動方向和殖民地與帝國連線的夾角。θ大，則算法全局搜索能力強，反之則算法更傾向于搜索當前區域。因此，控制好θ的大小極為重要，決定著優化結果的準確性。本文將基本ICA算法中由θ～U（-γ，γ）產生θ改為采用（24）和（25）混沌映射產生θ，以加強ICA算法的全局搜索能力。另外由于混沌映射的不重復性，算法的收斂速度也得到了提高。圖2為改進ICA算法的求解流程圖。

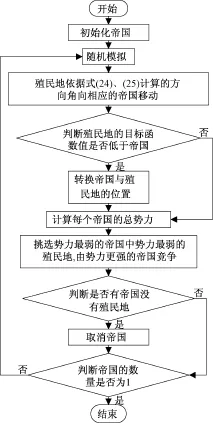
圖2 改進ICA算法的求解流程圖

4 算例分析

4.1 算例參數

為驗證所提模型和算法，對一個微網系統進行分析。取1 d為一個微網動態經濟調度周期，分為24個時段。從主網購買的旋轉備用最大值設為200 kW；DE、MT燃料成本相關參數參見文獻［20］；可控機組的CO2排放治理成本相關參照文獻［23］；其他微網系統相關參數見表1。

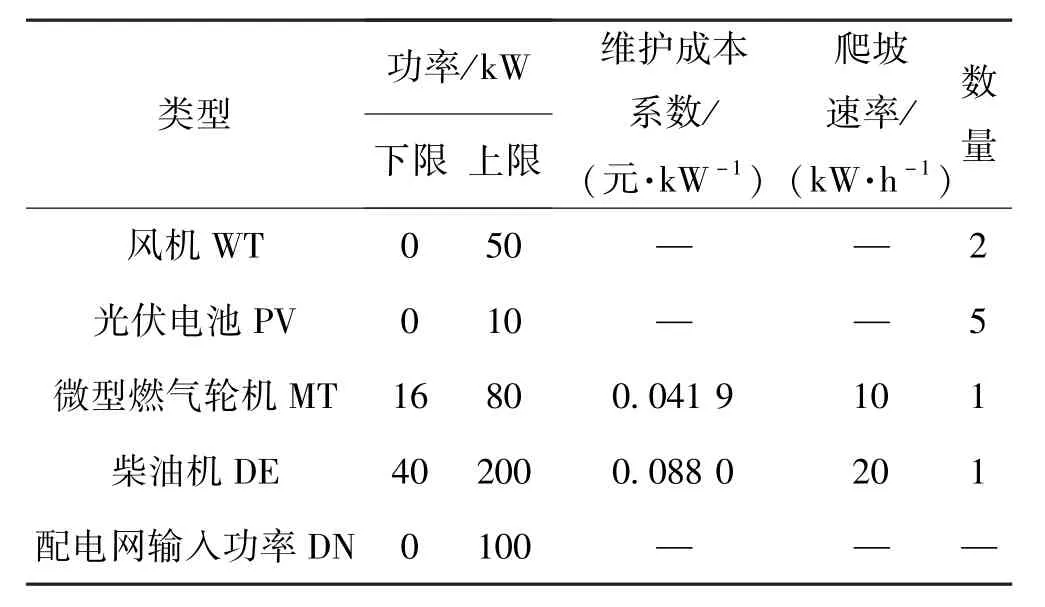
表1 微網系統參數

WT的風機特性參數和PV的電池特性參數參考文獻［12］和［17］。單個PV，WT的出力預測和負荷預測曲線見下圖3。DN的售電價格和從配電網購買的旋轉備用電價見表2。

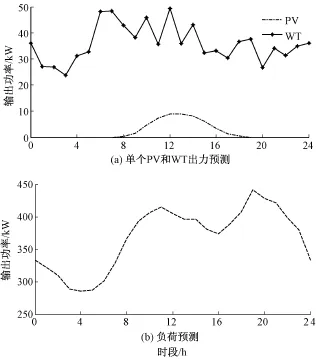
圖3 單個出力預測和負荷預測

利用Matlab進行仿真，初始國家數設為200個，初始帝國數設為20個，δ取為2，σ取0.2。隨機模擬次數設為1 000次。

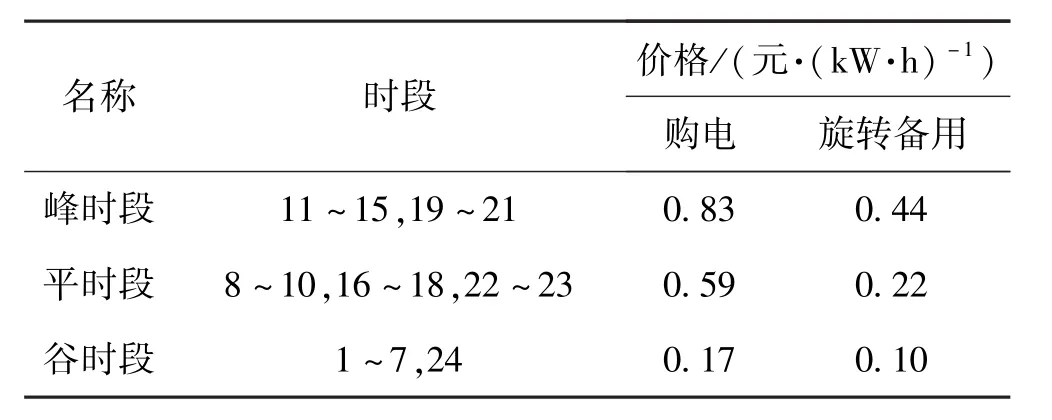
表2 購電價格和旋轉備用價格

4.2 算例結果與分析

4.2.1 參數β的影響

數學模型中參數β的選取會對優化結果產生影響，對目標函數式（8）進行優化，利用上述算法計算得到上述微網系統在不同參數β下的運行成本，見圖4。

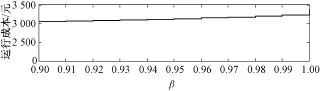
圖4 不同參數β下的運行成本

從圖4中可以看出，計劃運行成本隨著β的增大而逐漸增加，且在β接近1時增加幅度變大。

圖5是參數β為0.90，0.95，0.99和1.00下24時段調度結果。從圖中可以看出MT，DE和DN的輸出功率曲線在4種調度結果下變化趨勢基本相同，均受著分時電價的影響。這說明參數β的變化對MT，DE和DN的輸出功率基本沒有影響。而對于從配電網購買的旋轉備用容量，卻是隨著β的提高而增加，且β越大DN備用增加的幅度越大，尤其是當β從0.99增加到1.00時DN備用的增加最為明顯。這也就造成了運行成本的變化，β從0.90增加到0.95計劃運行成本增長2.31%，β從0.95增加到0.99計劃運行成本增長3.70%，而當β從0.99增加到1.00計劃運行成本卻增長了4.15%。可見參數β在越靠近1，β的變動對運行成本的影響越明顯。

從圖5（a）中可以看出在時段3、4、5，MT出力大于DE，且時段3和時段4 MT為滿載出力，而DE剩余容量則還有很多。由此可見MT優先DE出力，即MT發電成本低于DE，從時段6開始由于爬坡約束的限制，出現了MT出力小于DE且非滿載運行。

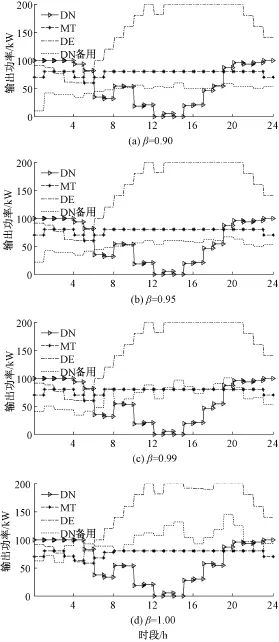
圖5 不同參數β下的調度結果

以上分析表明，微網可靠性評價指標β越大，即微網可靠性越高，則相應的運行成本越大。因此需要選擇合理大小的參數β，即能使微網可靠性滿足系統要求，又避免了不必要的成本浪費。

4.2.2改進算法的有效性分析

為驗證所提算法的有效性，選用遺傳算法（GA）、ICA和本文改進ICA算法進行比較，取β=0.99為例。計算結果列于表3。

表3 3種算法優化結果

可以看出，采用本文改進ICA算法的微網系統運行成本為3 234.7元，相比GA和ICA算法分別下降了36.1元和20.8元，結果優于其他兩種算法。

為了驗證改進ICA算法的性能，取β=0.99為例，在其他條件相同的情況下，微網系統的運行成本與迭代次數的關系如圖6所示。

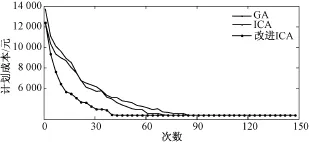
圖6 3種算法的計劃運行成本動態變化過程

可以看出:在迭代的前期三種算法的收斂性表現都比較好。但隨著計算的深入，本文所提改進ICA算法在迭代約50次后曲線變化不明顯，即其收斂速度好于GA算法和ICA算法。因此，本文所提改進ICA算法具有兩大優點:（1）算法的全局搜索能力更強；（2）算法具有更好的收斂性。

5 結論

（1）微網可靠性越高，則相應的運行成本越高；（2）所提改進ICA算法具有很好的收斂性和全局搜索能力。算例分析結果對微網動態經濟調度具有一定的指導作用和參考價值。

［1］ 黃偉，孫昶輝，吳子平，等.含分布式發電系統的微網技術研究綜述［J］.電網技術，2009，33（9）:14-18.

［2］ 李鵬，張玲，王偉，等.微網技術應用與分析［J］.電力系統自動化，2009，33（20）:109-115.

［3］ 苗雨陽，盧錦玲，朱國棟.基于改進多目標粒子群算法的微電網并網優化調度［J］.電力科學與工程，2012，28（7）:15-20.

［4］ 李銳，邱曉燕，任增，等.基于多通道迭代粒子群優化算法的微網經濟調度算法［J］.華東電力，2012，40（3）:453-457.

［5］ 寧陽天，李相俊，麻秀范，等.基于改進粒子群算法的微網動態經濟調度［J］.電力建設，2014，35（6）:26-30.

［6］ Atashpaz-Gargari E，Lucas C.Competitive Algorithm An Algorithm for Optimization Inspired by Imperialistic Competition［C］.IEEE Congress on Evolutionary Computation，Sirgapore，25-28September，2007:4661 -4667.

［7］ 張金環，安海霞，王永春.基于改進小生境帝國競爭算法的多目標電力系統無功優化［J］.華北電力大學學報（自然科學版），2014，41（4）:41-47.

［8］ Kayvanfar V，Zandieh M.The economic lot scheduling problem with deteriorating items and shortage:an imperialist competitive algorithm［J］.The International Journal of Advanced Manufacturing Technology，2012，62（5-8）:420-425.

［9］ Esram T，Chapman P L.Comparison of Photovoltaic Array Maximum Power Power Point Tracking Techniques［J］.IEEE Transactions on Energy Conversion，2007，22（2）:439-449.

［10］ 楊毅，雷霞，葉濤，等.考慮安全性與可靠性的微電網電能優化調度［J］.中國電機工程學報，2014，34（19）:3080-3088.

［11］ 張美霞，陳浩，楊秀，等.考慮風光和負荷隨機性的微網三相潮流計算［J］.中國電機工程學報，2013，33（13）:101-107.

［12］ 周瑋，孫輝，顧宏，等.計及風險備用約束的含風電場電力系統動態經濟調度［J］.中國電機工程學報，2012，32（1）:47-55.

［13］ 丁明，吳義純，張立軍.風電場風速概率分布參數計算方法的研究［J］.中國電機工程學報，2005，25（10）:107-110.

［14］ 王成山，鄭海峰，謝瑩華，等.計及分布式發電的配電系統隨機潮流計算［J］.電力系統自動化，2005，29（24）:39-44.

［15］ 程曉悅，盧錦玲.考慮不確定性的分布式電源多目標優化配置［J］.電力科學與工程，2014，30（11）:16-21.

［16］ Wen Z X，Shi L B，Xu Z，et al.Effects of wind power variability and intermittency on power flow［C］//2012 IEEE Power and Engineering Society General Meeting，San Diego，LA，USA，22-26 July，2012:1-7.

［17］ 翁振星，石立寶，徐政，等.計及風電成本的電力系統動態經濟調度［J］.中國電機工程學報，2014，34（4）:514-523.

［18］ 羅捷，吳俊明，陳德超，等.電動汽車參與下的虛擬電廠多目標優化調度［J］.電力科學與工程，2015，31（2）:50-54.

［19］ NREL.Energy modeling software for hybrid renewable energy systems［EB/OL］.2013.http//www.homerenergy.com.

［20］ Basu A K.Microgrids:Planning of fuel energy management by strategic deployment of CHP-based DERs-An evolutionary algorithm approach［J］.Electrical Plower and Energy Systems，2013，44（1）:326-336.

［21］ 王金全，黃麗，楊毅.基于多目標粒子群算法的微電網優化調度［J］.電網與清潔能源，2014，30（1）:49-54.

［22］ 竇鵬沖，李鵬.計及微網實時電價的并網運行控制策略［J］.電網與清潔能源，2014，30（8）:8-12.

［23］ Panigrahi B K，Pandi V R，Das S，et al.Multiobjective fuzzy dominance based bacterial foraging algorithm to solve economic emission dispatch problem［J］.Energy，2010，35（12）:4761-4770.

［24］ May R M.Simple mathematical models with very complicated dynamics［J］.Nature.1976，261（5560）: 459-467.

Dynamic Economic Dispatch of MicroGrid Using Improved Imperialist Competitive Algorithm

Zhai Yunfeng，Yi Guowei，Wang Yi，Li Ming，Zhou Peng
（College of Electrical and Information Engineering，Changsha University of Science and Technology，Changsha 410004，China）

Considering the influences of the uncertainty of the photovoltaic power generation，wind power generation and load in microgrid，this paper sets up a mathematical model of microgrid dynamic economic dispatch based on chance constrained programming on the premise of each constraint of the system.The following costs:the minimum total operation costs of the microgrid，the controlled unit fuel costs，the emission control cost of carbon dioxide，the unit maintenance costs，the active power buying costs and spinning reserve buying costs from distribution network，have been taken into consideration.This paper used probability constraints to depict the reliability of the microgrid operation，and considered the output constraints and climbing constraints of the controlled units.In order to solve the problems that imperialist competitive algorithm tends to fall to local minimum easily and converge slowly，an improved imperialist competitive algorithm is proposed to improve the mathematical model by introducing the chaos theory and stochastic simulation technology.Finally，taking an microgrid system as an example，this paper analyses the influence of microgrid economy and the scheduling results in different reliability probability level.It also compares the convergence properties of the algorithm with the conventional algorithm in order to verify the effectiveness of the algorithm.

microgrid；chance constrained programming；dynamic economic dispatch；imperialist competitive algorithm；chaotic map

TM73

A DOI:10.3969/j.issn.1672-0792.2015.05.007

2015-03-31。

湖南省高校創新平臺開放基金項目（編號10K003）。

翟云峰（1989-），男，碩士研究生，主要研究方向為微網系統經濟調度，E-mail:278148454@qq.com。