基于EMD—SVM的農產品市場價格短期預測模型

屠星月　于輝輝　郭承坤等

摘要：基于傳統計量經濟預測方法無法解決非線性、小樣本的價格預測的問題，建立了基于EMD（經驗模態分解）-SVM（支持向量機）的農產品市場價格短期預測模型，以1997-2011年中國農產品集貿市場小麥月度價格序列為例對其進行方法應用。結果表明，與常用傳統計量經濟預測方法和智能化模型比較，基于EMD-SVM的農產品市場價格預測模型精度有明顯提高，提供了適用于中國農產品波動規律的農產品價格短期預測的新方法和借鑒。

關鍵詞：時間序列；經驗模態分解；支持向量機；農產品價格預測

中圖分類號：F323.7；O141.4；S-9 文獻標識碼：A 文章編號：0439-8114（2015）19-4903-05

DOI：10.14088/j.cnki.issn0439-8114.2015.19.063

Abstract： The prediction method of traditional econometric is still unsolvable for nonlinear and small scale price prediction，based on the problem， the EMD-SVM prediction model for market price of agricultural product was build. Taking the monthly time series of wheat price in Chinese terminal market in 1997-2011 as example， the method application of the model was conducted to test its accuracy. Results showed that， compared with common econometric prediction models and intelligent models， the accuracy of SVC was obviously improved by combining with EMD. Therefore， a new method and reference for short-term price prediction applicable to the regular fluctuation Chinese agricultural product was put forward.

Key words： time series；EMD；SVM；price prediction of agricultural product

農產品市場價格預測，是政府管理決策、農業人員生產經營管理的重要依據。近年來，中國農產品市場價格波動頻率快，波動幅度大，并呈現出非平穩、非線性等不規律波動特征，增加了農民生產安排、管理部門市場調控、政府管理決策的難度。因此科學準確地開展農產品價格預測，能夠為社會提供具有前瞻性的市場信息服務，對有效指導農業生產經營管理具有重要意義[1]。

傳統計量經濟學基于價格時間序列進行統計分析與預測，是目前廣泛應用的農產品價格預測方法，例如ARIMA、Holt-Winters、CensusX12季節調整法、ARCH模型等。王川等[2]依據時間序列數據特征篩選出雙指數平滑模型、Holt-Winters乘法模型和ARIMA（1，1，4）模型進行加權組合實現了中國蘋果市場價格短期預測；李干瓊等[3]綜合利用季節虛擬變量法、Census X12法、移動平均比率法、Holt-Winters季節指數平滑法、SARIMA法等建立了組合短期預測模型，結果表明組合模型預測的精度高于單項時間序列模型。然而隨著市場價格波段逐漸向復雜化、非線性化、不規則化發展，該類方法反映出一定局限性。因此，基于智能化模型如支持向量機（Support vector machine， SVM）、神經網絡、混沌時間序列的預測方法逐漸成為農產品市場價格預測的熱點[4-6]。其中，建立在統計學理論基礎上的SVM方法在時間序列預測方面具有可以有效縮小泛化誤差區間、降低模型的結構風險、同時又保證樣本預測誤差最小的優點[7]。近年來，一些學者針對近期農產品市場價格的不規則、非線性波動特點，探索研究了SVM方法對農產品價格預測的應用。陳兆榮等[8]用SVM模型對ARIMA模型的預測誤差進行預測，實現了兼顧時間序列線性特征和非線性特征的ARIMA-SVM農產品價格預測組合模型，預測結果顯示組合模型比單個ARIMA、SVM 模型預測精度高。趙辰陽等[4]利用粒化計算的思想將農產品市場價格序列提升到上層粒度序列，通過SVM對新形成的粒化序列進行預測形成預測區間，最后根據實測值與預測值的對比結果判斷預測方法的優劣，提出了基于FIG-SVM 的農產品價格趨勢預測方法，結果表明，該方法預測精度較高，能夠應用于實際場景。韓延杰[9]將原始價格數據進行模糊信息粒化，然后利用支持向量機對粒化后的價格數據做出預測，為提高預測精度，利用遺傳算法對支持向量機的參數進行優化，結果表明，該方法能對農產品價格的變化范圍進行有效地預測。然而SVM方法單獨應用于農產品時間序列價格預測時，容易出現預測滯后和拐點處誤差較大的問題，現今基于EMD的智能化模型預測已逐漸應用于氣象、工業、金融等領域，并驗證了該方法的可行性和有效性[10-14]。

本研究引入了經驗模態分解（Empirical mode decomposition，簡稱EMD）將價格序列分解為具有不同尺度特征的模態分量的疊加，并將這些具有平穩性、周期波動性的分量作為SVM的輸入變量分別進行預測，并將預測結果疊加，從而獲得農產品價格。選取1997-2011年中國農產品集貿市場小麥月度價格序列為例對EMD-SVM模型進行方法應用，并將結果與常用計量經濟預測方法及SVM方法預測結果進行對比分析，驗證了該方法的可行性和精確性。

1 研究方法

1.1 EMD方法原理

EMD是由美國國家宇航局N. E. Huang等于1998年提出的一種新型自適應信號時頻處理方法，該方法依據數據自身的時間尺度特征進行信號分解，分解結果為一系列具有不同尺度、平穩性和周期波動性特征的本征模函數（Intrinsic mode function，IMF）和一個代表原始信號總體趨勢的剩余分量，其中每個IMF必須滿足如下兩個條件：①在整個信號序列上，極值點的個數和過零點的個數相差不大于1；②在任意點處，上下包絡的均值為0，其分解結果能夠反映真實的物理過程，因此適用于處理非平穩、非線性的信號[15]。

EMD方法基于以下3個假設進行運算和分解：①任何信號都是由若干本征模態函數組成的； ②各個本征模態函數即可是線性的，也可是非線性的，各本征模態函數的局部零點數和極值點數相同，同時上下包絡關于時間軸局部對稱； ③在任何時候，一個信號都可以包含若干本征模態函數，若各模態函數之間相互混疊，則組成復合信號。

1.2 SVM回歸方法原理

SVM是由C C等[16]于1995年提出的基于統計理論、VC維（Vapnik-Chervonenkis dimension）和結構風險最小化模型算法設計的機器學習算法。該方法的基本思想是將低維不可分的數據轉化到高維空間進行處理，即通過核函數定義的非線性映射將低維輸入空間轉化到高維空間使其線性可分，在高維空間中利用線性的方法分析輸入變量和輸出變量之間的非線性關系。該方法由于以機構風險最小化為基礎，因此對推廣錯誤的上界進行約束和減少，推廣性能優越，不存在神經網絡等算法的過度適應問題，實現了低維數據到高維數據的映射及在高維空間使用線性函數實現分類，核函數的使用解決了以往存在的維數災難問題。

1.3 EMD-SVM模型設計

現今研究中基于SVM的價格時間序列預測，一般利用若干期時間序列滯后的序列值作為SVM的輸入樣本，該過程中，隨著時間序列的復雜性增加，不平穩性增加，SVM所需的滯后輸入樣本也會增加，EMD分解能夠獲得平穩的IMF分量和體現序列整體趨勢的余量，減少了隱含信息的干涉和耦合，并可依據不同IMF分量的特點分別選擇不同核函數進行SVM預測，從而提高精度。因此本研究建立了EMD-SVM預測模型，利用EMD對原始價格序列進行分解，利用EMD分解獲得的具有平穩性、周期波動的若干價格序列分量為輸入樣本分別進行SVM預測，并將各分量的預測結果疊加從而獲取價格預測值，具體如下。

首先，利用EMD對原始價格時間序列P（t）進行分解，獲得m個imfi（t）為本征模態函數IMF分量，和rm（t）為趨勢分量。

2 EMD-SVM預測模型應用實例

2.1 數據樣本選擇

本研究所用實驗數據為中國知網2012、2008、2007、2004年統計年鑒中全國農產品集貿市場小麥月度價格走勢數據，考慮樣本的可獲得性和連續性，最終選擇數據周期為1997年3月至2011年12月共178個數據樣本（圖1），該數據為等間隔價格時間序列數據，該序列隨時間呈不穩定、不規則波動，后期波動中具有一定周期性。

實驗研究中利用1997年3月至2010年12月的166個樣本作為訓練樣本、2011年12個月的樣本作為測試樣本進行預測模型應用與驗證。

2.2 評價標準

2.3 EMD-SVM預測模型應用

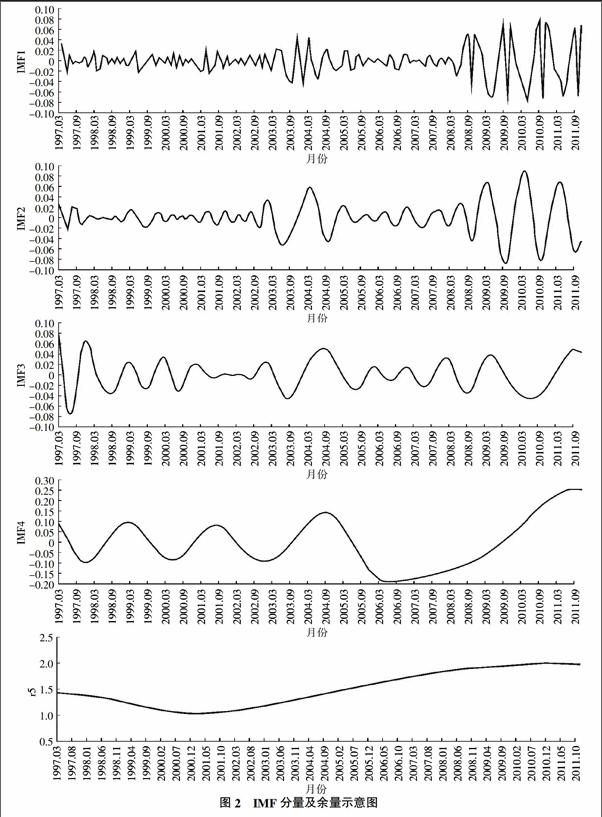
由圖2可見，文中小麥價格時間序列具有不穩定、非線性的特征，因此可利用EMD方法對小麥價格時間序列進行分解，利用Matlab R2014a調用EMD工具箱編寫程序對其進行分解獲取4個IMF分量及1個線性趨勢余量。分解結果如圖2所示，圖中前4個為IMF分量，最后1個為余量，可發現IMF1與IMF2分量波動劇烈但整體平穩，IMF3、IMF4分量變化逐漸緩慢且規律性較強，r5即余量，與原價格序列整體趨勢一致，反映了價格序列的線性趨勢。

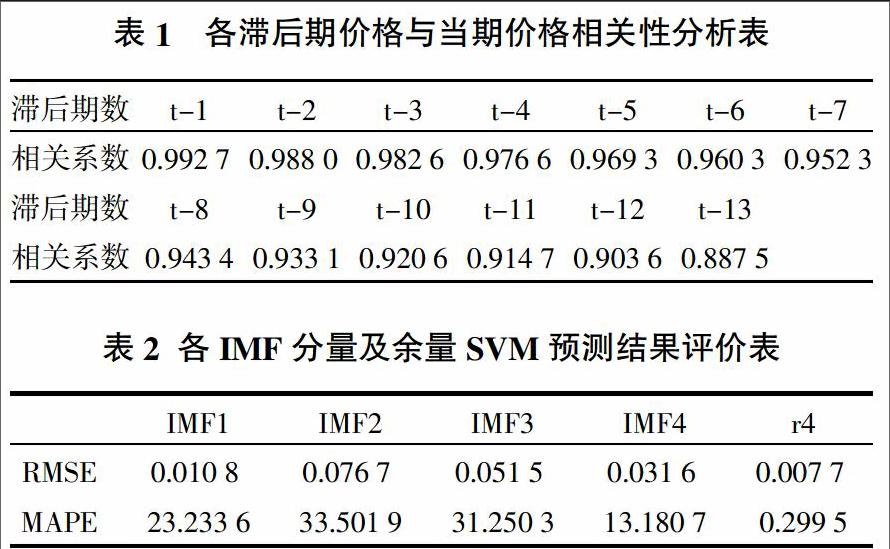
常用的核函數有多項式核函數、徑向基（RBF）核函數、多層感知器核函數等。依據EMD各分量及余量的波動特征，選擇不同核函數進行SVM預測，其中對IMF1和IMF2采用RBF核函數進行預測，對IMF3、IMF4采用多項式核函數進行預測，對余量r5采用線性核函數進行預測，預測中滯后期數的選擇依據價格序列中滯后期與當期的相關性系數進行確定，具體如表1所示，可見隨著延遲時間增長，相關性遞減。因此選用相關系數大于0.95的滯后數據進行預測，即選用滯后1期到滯后7期的數據進行SVM預測，預測結果評價如表2所示，發現對高頻IMF分量的SVM預測效果不是很理想，隨著頻率降低，預測精度逐漸升高，但高頻分量的幅值較小，因此對最終的預測結果影響較小。

最后對EMD分量及余量的SVM預測結果進行疊加，獲得最終預測結果。

2.4 預測結果評價與分析

為對EMD-SVM的預測精度進行進一步對比分析，采用了常用的計量經濟模型Holt-Winters、常用的智能分析方法神經網絡、SVM方法對該時間序列進行預測，預測結果評價如表3所示，觀察各方法的預測結果折線圖（圖3），發現結合EMD分解方法的SVM預測精度顯著高于單獨運用SVM方法預測，同時EMD-SVM不僅整體預測精度高于其他常用方法，且在時序拐點（如圖3中的2011年11月）部分的預測結果顯著優于其他方法，因此驗證了該方法的可行性和有效性。

3 結論與展望

針對傳統計量經濟預測方法難以預測非線性不規則價格時間序列、SVM方法在序列拐點預測效果較差的問題，建立了EMD-SVM價格序列預測模型。通過EMD方法對時間序列進行分解，將分解后獲得的IMF分量和余量R進行SVM預測，將預測后的分量和余量進行疊加獲得預測價格，并選用中國農產品集貿市場小麥月度價格序列進行實例驗證和分析。預測結果表明：①引入EMD方法對時間序列進行分解，可依據各分量和余量的波動特征分別選擇不同SVM核函數進行預測，削弱了預測中相鄰頻帶的相互干擾，增加了SVM預測的靈活性，依據預測結果評價可發現EMD-SVM模型的預測結果精度高于單獨應用SVM方法，且改善了SVM方法在時序拐點預測中誤差較大的問題。②EMD-SVM模型預測結果與常用計量經濟預測模型、神經網絡模型相比預測精度較高，因此證明了該方法的優勢。③預測中SVM模型預測中的估計參數依靠交叉驗證確定，而該方法耗時較長，且精度不高，因此在今后的研究中，如何確定各分量、余量、SVM預測中的估計參數有待探索驗證。由于數據獲取的限制，本研究中僅利用價格時間序列進行預測，今后研究中可考慮利用多影響因素的農產品價格預測。

參考文獻：

[1] 任偉宏.農產品市場價格預測方法探析[J].中國農學通報，2011（26）：209-212.

[2] 王 川，趙俊曄，趙友森.組合預測模型在農產品價格短期預測中的應用——以蘋果為例的實證分析[J].系統科學與數學，2013（01）：89-96.

[3] 李干瓊，許世衛，李哲敏，等.農產品市場價格短期預測方法與模型研究——基于時間序列模型的預測[J].中國農業大學學報，2011（02）：172-178.

[4] 趙辰陽，徐 明.基于FIG-SVM的農產品價格趨勢預測[J].江蘇農業科學，2014（05）：385-388.

[5] 彭 琳，林 明.基于NARX神經網絡的農產品價格時間序列預測方法研究[J].農機化研究，2013（11）：18-21.

[6] 魏明樺，鄭金貴.基于改進BP神經算法的農產品價格預測模型的構建與實現[J].唐山師范學院學報，2014（02）：66-68.

[7] V，V.The nature of statistical learning theory[M]. New York： Springer，1999：78-82.

[8] 陳兆榮，雷勛平，王 亮，等.基于ARIMA-SVM組合模型的我國農產品價格預測研究[J].財經理論研究，2013（02）：103-107.

[9] 韓延杰.一種基于模糊信息粒化和GA-SVM的農產品價格預測方法[J].農業網絡信息，2012（11）：16-20.

[10] 尹東陽，盛義發，李永勝.基于EMD和RBFNN的短期風速預測[J].電氣技術，2014（06）：44-47.

[11] 郝 瓊，劉毅敏.EMD-SVM組合模型在帶鋼張力預測中的應用[J].計算機測量與控制，2014（04）：1279-1281，1284.

[12] 葉 林，劉 鵬.基于經驗模態分解和支持向量機的短期風電功率組合預測模型[J].中國電機工程學報，2011（31）：102-108.

[13] 王義康.EMD-SVM非線性組合模型對高爐鐵水含硅量的預測[J].中國計量學院學報，2008（04）：355-359.

[14] 朱倩雨，覃錫忠，賈振紅.融合EMD與全局版人工魚群LS-SVM的網絡流量預測[J].激光雜志，2014（05）：42-46.

[15] HUANGN N E，SHEN Z，LONG S R.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society，1998，454（1971）：903-955.

[16] C C，V V.Support-vector networks[J].Machine Learning， 1995（3）：273-297.