基于多層感知器神經網絡的小微企業信貸風險研究

周駟華 汪素南

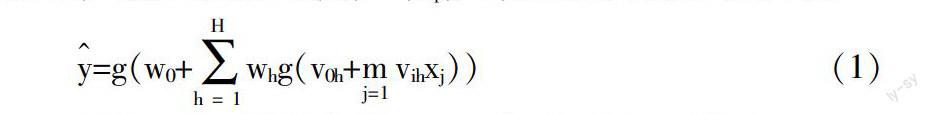
摘要：文章以多層感知器神經網絡算法為基礎，對某小貸公司的小微企業信貸數據庫中的信貸記錄進行了信貸評估，并將該結果與決策向量機、線性判別、二次判別和邏輯回歸等數據挖掘方法進行了比較。分析結果表明，從總體上看，多重感知器神經網絡算法優于傳統的基于參數的分類方法，即多層感知器神經網絡算法擁有相對較高的ROC曲線下面積和較低的預期錯誤分類成本。更進一步，在研究所采用的4種MLP算法中，基于BFGS Quasi-Newton訓練算法的MLP表現最為出色，可以作為金融機構進行小微信貸風險評估的輔助決策模型。

關鍵詞：多層感知器神經網絡；小微企業；信貸評估；數據挖掘；輔助決策模型

一、 引言

根據《全國小型微型企業發展情況報告》（2014），截至2013年末，全國各類企業總數為1，527.84萬戶。其中，小微企業1，169.87萬戶，占企業總數的76.57%。如將4，436.29萬戶個體工商戶納入統計范圍，小微企業所占比重達到94.15%。我國的小微企業創造GDP價值占總量的60%，納稅占總量的50%，完成了65%的發明專利和80%以上的新產品開發。然而，根據《中國小微企業白皮書》顯示，目前我國小微企業融資缺口高達22萬億元，超過55%小微金融信貸需求未能獲得有效支持。

如何有效地評估小微企業的信貸風險，對學界和業界都是一個挑戰。根據Blanco等[7]的建議，采用自動信用評分系統能夠加快信貸審批速度，降低貸前分析成本并減少人為因素對信貸審批的影響。因此，從理論上研究小微企業信用風險預警體系，調整商業銀行對小微企業的風險評價模式，構建專門的小微企業信用風險預警模型，是解決小微企業融資難問題的一個重要途徑。

進入20世紀90年代，基于數據挖掘的信用風險評價方法大幅度提高了預測的精度，以人工神經網絡（ANNs）為代表的非參數分析方法已廣泛應用于企業財務危機預警分析。ANNs信用風險模型以其較強的逼近非線性函數的優勢從眾多方法脫穎而出，其對歷史數據的模擬仿真和預測能力也顯示了獨特的優勢。然而，由于ANNs自身的限制和理論上的不完善，單一利用ANNs來評估信用風險的效果往往不理想，且信用風險評估是一個綜合因素作用的過程，而多層感知器（MLP）神經網絡所追求的目的就是基于多因素評估結果的最優決策。為了突破傳統ANNs的局限，本文引入MLP對小微企業的信用風險進行評估研究，并將結果和傳統的線性判別（LDA），二次判別分析法（QDA）和邏輯回歸（LR）進行比較。

二、 文獻綜述

小微企業信貸風險評估主要包括兩個方面：（1）對新申請者做出判斷；（2）貸后違約預測。以往，學界研發了大量的方法和模型加速信貸決策的過程。如線性判別分析和邏輯回歸是兩類最常用的用于構造信貸風險評估模型的線性統計工具。然而，有學者指出，在現實環境下，由于LDA所依賴的兩個假設，即輸入變量服從多元正態分布，違約和非違約樣本的色散矩陣或方差-協方差矩陣相等通常得不到滿足，因而精度欠佳。

ANNs的出現有效地彌補了傳統方法的不足。由于ANNs具備在復雜環境下利用大量不確定信息對研究群體進行分類的能力，因而近年來被廣泛應用于對復雜過程的估計和預判。神經網絡也稱人工神經網，是近年來信用評估領域的熱點方法，作為一門新興的信息處理科學，ANNs對人腦若干基本特征進行抽象和模擬，以人的大腦工作模式為基礎，研究自適應及非程序信息處理方法。ANNs的優點是對數據的分布要求不嚴格，也不要求詳細表述自變量與因變量之間的函數關系，能有效解決非正態分布、非線性信用評估問題。但神經網絡也有自身的缺點，即為了獲得最優的網路而導致訓練時間過長和難以辨別輸入變量的相對重要性。

在ANNs方法中，多層感知器（MLP）神經網絡因其出色的性能而被應用于風險評估領域。Werbos創立的反向傳播算法已被廣泛應用于MLP。MPANN（Memetic pareto artificial neural networks）通過多目標進化算法和以梯度為基礎的局部搜索對BP算法進行優化。

對神經網絡的改進包括改變訓練的比率和測試數據庫，隱藏階段的數目和訓練循環等。Khashman通過對德國數據集進行研究，通過9種學習方案對不同的訓練/驗證比數據進行了研究。結果發現，用400個例子做訓練并用600個例子總驗證的學習方案表現最佳，總準確率達83.6%。情感神經網絡是一類改進的BP學習算法，它通過兩個額外的情感參數——焦慮和自信對情感權重進行更新。通過將情感神經網絡和傳統的神經網絡進行對比，Khashman發現傳統的神經網絡和情感神經網絡都有效，但情感神經網絡在速度和準確率方面更勝一籌。另一種改善MLP的方法是人工突出可塑性MLP，其在某種分類僅有少數幾種可用模式或當小概率時間包含的信息對成功應用至關重要時特別有效。通過運用可塑MLP，Marcano-Cedeno等在德國數據集上獲得了84.67%的準確率，在澳大利亞數據集上獲得了92.75%的準確率。

三、 實證研究

1. 數據集。本文使用某小貸公司小微信貸數據庫中的信息，數據的時間跨度從2010年至2014年。其中包含以下幾類信息：

（1）小微企業法人或實際控制人的個人信息；

（2）小微企業經濟和財務比率數據；

（3）小微企業當前信貸數據；

（4）宏觀經濟數據。

經過初篩并剔除異常記錄，共獲得5 434個小微企業樣本。根據某絕大多數金融機構的定義，貸款逾期超過15天即算貸款違約。其中4 766個小微企業未發生貸款違約，占比為87.85%，剩余668個小微企業都存在不同程度的貸款違約，占比為12.15%。為了對分類模型（LDA、QDA、LP、SVM和MLP）進行有效對比，本文將數據集隨機分為兩個不相交的子集，其中75%的樣本作為訓練子集，25%的樣本作為測試子集。測試子集總計包含1 359個小微企業樣本（13.23%的小微企業發生貸款違約，86.77%的小微企業未發生貸款違約）。每一個模型都采用10次交叉檢驗。采用交叉檢驗的優點在于信貸模型能夠最大限度地包含可用數據（75%的樣本）。

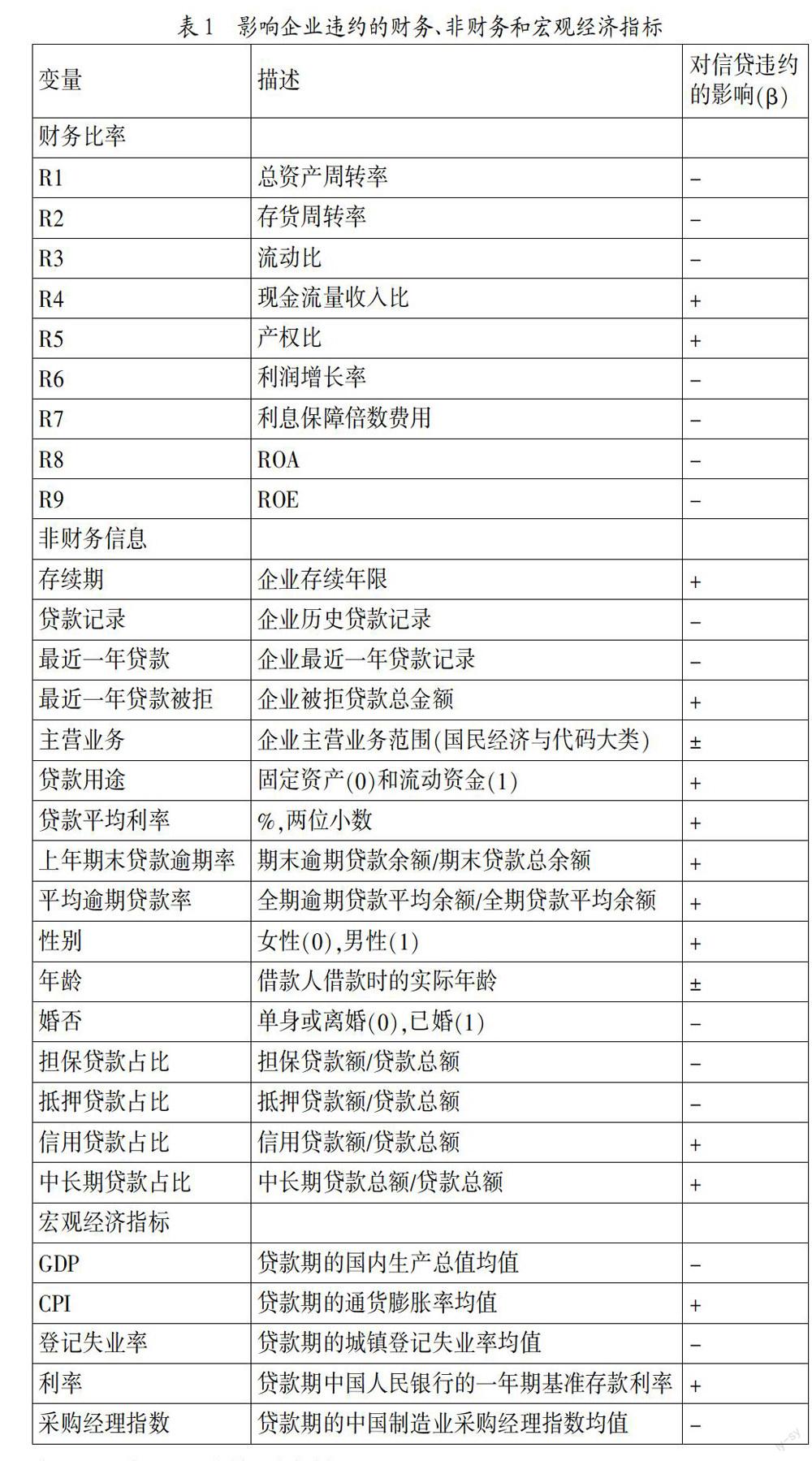
2. 數據描述。小微企業信貸風險評估的首要工作是構建一個適合小微企業特點的信用風險評估指標體系。結合我國的具體國情，參照沈軍彩和徐繼紅，Blanco等，Mittal等的指標設置，本文選擇9個財務指標，16個非財務指標和5個宏觀經濟指標（見表1）。本次研究特色之一是指標體系包含了影響小微企業信貸履約情況定性指標。之所以選擇這些指標，主要有以下考慮：（1）Schreiner認為，相比大中型企業，由于小微企業自身的原因，無法全面量化運營數據。因此，部分信貸數據以定性和非正式形式記錄；（2）Blanco等的研究表明，在信貸風險評估模型中加入定性指標，有助于提高模型的預測能力。此外，由于借款人的履約能力與宏觀經濟狀況存在密切聯系，因此在信貸風險評估模型中加入宏觀經濟變量能夠增強模型的解釋和預測能力。因變量方面，采用二進制變量，0=沒有違約，1=產生違約。

3. 研究方法和實驗設計。國內外關于ANNs在信貸風險評估中的應用類型包括模式神經網絡、概率神經網絡、擴展學習向量器和多層感知器（MLP）等。其中，MLP是在商業領域應用最為廣泛的一類ANNs模型。根據相關研究，本文采用三層感知器（圖1），其中輸出層為單個違約概率判別節點。這一值由邏輯神經元激活函數g（u）=eu/（eu+1）獲得。以H代表隱蔽層的規模，{vih，i=0，1，2，…，p，h=1，2，…，H}作為p個輸入和第一層之間突觸權重，{wh，h=0，1，2，…，H}作為連接隱藏節點和輸出節點之間的突觸權重。由此，當輸入向量為（x1，…，xp）時，ANNs的輸出結果為：

y=g（w0+whg（v0h+vihxj））（1）

輸出的結果即為根據輸入參數獲得的違約概率。通過將y與閾值進行比較（如0.5），就能對申請企業的貸款違約進行預判，如y>0.5則表明，申請人貸款違約的概率較大。

在輸入數據之前，本文首先通過線性回歸模型對變量進行篩選，選擇具有統計顯著性的變量作為輸入參數（p≤0.05），且預測變量都線性分布在[-1，1]之間。Matlab和R作為工具，對MLP和其他算法進行分析。

R的神經網絡工具箱具備對擬牛頓法（Quasi-Newton）算法運用BFGS過程分析單隱蔽層ANNs的功能。參考Blanco等的方法，令W=（W1，…，WM）為網絡的M個相關系數矩陣，令yi（i=1，…，n）為違約標識，1代表違約，0代表沒有違約，同時，為了避免過度擬合，特引入衰減項λ。對于分類問題，合理的誤差函數就是熵的條件最大化標準。因此，可得如下函數：

（yilnyi+（1-yi）ln（1-yi））+λ（W2i）（2）

在R中部署MLP模型需要指定兩個參數：隱蔽層的規模（H）和衰減項λ，因此，需通過10次交叉驗證搜索隱蔽層（H）和格點{1，2，…，20}×{0，0.01，0.05，0.1，0.2，…，1.5}。Matlab包含的神經網絡工具箱，也能對MLP模型進行求解。有6種常用的算法可以用作訓練規則，分別是Gradient descent、Gradient descent with momentum、BFGS Quasi-Newton、Levenberg-Marquardt、Scaled conjugate gradient和Resilient back-propagation。這6種算法的基本思想都是使誤差平方和最小：

（yi-yi）2（3）

在判別準則方面，本文采用ROC曲線下面積（AUC）、測試準確率、I類錯誤率、II類錯誤率和預期錯誤分類成本（EMC）。其中，AUC是反映連續變量敏感性和特異性的綜合性指標，它用構圖法揭示敏感性和特異性的相互關系并通過連續變量設定出多個不同的臨界值，從而計算出一系列敏感性和特異性，再以敏感性為縱坐標、（1-特異性）為橫坐標，曲線下面積越大，診斷準確性越高。EMC的定義如下：

EMC=C21P21π1+C12P12π2（4）

其中，π1和π2分別是優質與不良的信貸群體的先驗概率，P21和P12分別是I類錯誤和II類錯誤的概率。其中，P21是優質信貸群體被誤判為不良信貸群體的概率，P12則是不良信貸群體被誤判為優質信貸群體的概率。π1和π2是優質信貸群體和不良信貸群體的比例。

為比較MLP與其他模型的有效性，本文將MLP模型與傳統的LDA、QDA、SVM和LR進行比較。其中，SVM采用徑向基核函數（RBF）。在MLP參數設置方面，設定學習精度ε=0.000 1，最大訓練次數為1 000，根據Kolmogorov定理設置隱含層節點數65。在LDA和QDA參數設置方面，最小化10次交叉驗證的誤差門檻值為0.35。在LR參數設置方面，最小化10次交叉驗證的誤差門檻值為0.58。在SVM參數設置方面，需要指定懲罰系數-c與核參數-γ，通過對RBG徑向基核函數的最優參數篩選，確定c=512，γ=0.008 563作為建立模型的基本參數，構造SVM分類評估模型。

4. 對比分析。表2總結了MLP的6種訓練算法、SVM、LDA、QDA、LR的測試結果。從中可以看出，基于BFGS Quasi-Newton訓練算法的MLP獲得最高的AUC（0.961），最高的測試準確率（88.54%），最低的II類錯誤率（16.43%）和最低的EMC（0.432）。I類錯誤率最低（3.66%）的是基于Scaled conjugate gradient訓練算法的MLP，但與之相伴的是最高的II類錯誤率（22.54%）。從圖2（各模型的AUC值和EMC值）的分布可以看出，基于BFGS Quasi-Newton 訓練算法的MLP效果最佳，位于圖2的右下部，該算法3層感知器結構，由20個輸入節點、3個隱藏借點和1個輸出節點構成，采用10次交叉驗證，衰減項λ=0.2。基于BFGS Quasi-Newton 訓練算法的MLP之所以能夠取得最高AUC值和最低EMC值，是引入了二階訓練算法的緣故。根據本文使用的樣本數據，二階訓練算法的效果比傳統的梯度下降（Gradient descendent）算法更有效，這一結果與之前的一些研究結果相吻合。此外，傳統的方法，如LDA、QDA和LR無論在AUC值還是EMC值方面，都明顯弱于MLP二階訓練方法，如BFGS Quasi-Newton、Levenberg-Marquardt、Scaled conjugate gradient和Resilient back-propagation等。在參數模型方面，LDA和QDA的AUC值都明顯低于LR（0.937），這一結果與West和Lee等的結論相一致，即LR優于LDA和QDA。然而，本次研究的所有參數模型中，LDA擁有最高的測試準確率（86.49%），QDA擁有最低的EMC（0.515）。因此，很難對本次研究的三個參數模型，LR、LDA和QDA的優劣做出評判，同樣，采用I類錯誤率和II類錯誤率也很難做出明顯的評價。

從總體看，非參數模型不僅擁有較高的AUC和較低的錯誤分類成本。此外，盡管存在黑箱屬性等，但在小微企業信貸風險評估方面，MLP仍不失為一種較為優良的方法。正如West指出的，對金融機構而言，即使提高1%的預測精度，也能帶來數億的利潤。就測試準確率而言，最優的MLP算法與其他算法的差別從0.72（Levenberg-Marquardt）到3.31（QDA）。因此，部署基于MLP的神經網絡算法的確能夠顯著降低小微信貸的損失。再者，采用諸如ANNs等非參數方法，還能帶來管理方面額優勢，如更符合Basel II的內部評級法所規定的資本充足率要求等。

四、 結論

本文構建了一個包含企業財務指標，非財務指標和宏觀經濟指標的小微信貸評價指標體系。通過對某小貸公司小微數據庫內的樣本進行測試，本文對4種MLP神經網絡算法、1種決策向量機和3種傳統的基于參數的分類方法進行了分析。實證結果表明，MLP從總體上優于傳統的基于參數的分類方法，在4種MLP算法中，基于BFGS Quasi-Newton訓練算法的MLP表現最為出色，可以推薦企業使用。此外，本文將企業的信貸評價指標作為模型的學習樣本，進行評估推理知識學習，具有一定的動態特性，金融機構在實際使用過程中，可以酌情增刪指標，以提高模型的預測精度。最后，正如李曉峰和徐玖平所言，ANNs使用非線性函數更貼近復雜的非線性動態經濟系統，擺脫了古典經濟學賴以生存的線性分析工具，能夠更為準確地反映企業的信息，故比傳統方法具有更大的優勢，這為企業信用的綜合評估提供了可行的途徑。

參考文獻：

[1] 國家工商總局全國小型微型企業發展報告課題組. 全國小型微型企業發展情況報告（摘要）[N].中國工商報，2014-03-29.

[2] 郭文偉，陳澤鵬，鐘明.基于MLP神經網絡構建小企業信用風險預警模型[J].財會月刊，2013，（6）：22- 26.

[3] 胡海青，張瑯，張道宏.供應鏈金融視角下的中小企業信用風險評估研究——基于SVM與BP神經網絡的比較研究[J].管理評論，2012，24（11）：70-80.

[4] 宿玉海，彭雷，郭勝川.基于BP神經網絡的商業銀行信用風險模型改進探究[J].山東財政學院學報，2012，118（2）：12-19.

[5] 高尚.支持向量機及其個人信用評估[M].西安：西安電子科技大學出版社，2013.

[6] 沈軍彩，徐繼紅.神經網絡的企業信用風險評估應用研究[J].計算機仿真，2012，29（3）：254-257.

[7] 李曉峰，徐玖平.商業銀行客戶信用綜合評估的BP神經網絡模型的建立[J].軟科學，2010，24（2）：110-113.

作者簡介：周駟華（1978-），男，漢族，上海市人，浦發銀行博士后科研工作站、復旦大學工商管理博士后流動站博士后，研究方向為小微企業金融服務、供應鏈金融；汪素南（1966-），男，漢族，浙江省金華市人，上海浦東發展銀行零售業務總監，博士后科研工作站導師，研究方向為零售銀行金融服務。

收稿日期：2015-07-11。