一種基于遺傳算法的混合濾波器組設計方法

譚富春，呂幼新，楊皓翔

(電子科技大學電子工程學院， 成都611731)

0 引言

模數轉換器(ADC)作為數字化電子系統的重要組成部分，是決定整個系統性能優劣的一個很重要的模塊單元。隨著現代電子技術的發展，對數據采集的精度和速率都提出了越來越高的要求，而受目前器件本身的限制，單片ADC很難同時滿足高精度、高速率的采樣要求。

Velazquez［1］提出了利用混合濾波器組(Hybrid Filter Banks，HFB)來實現高精度、高速率的模數轉換系統，這也是目前備受學者們關注的研究重點和難點。文獻［2］應用Z-S變換方法設計實現了模擬分解濾波器組，利用IFFT算法設計得到了數字綜合濾波器的系數。此方法雖可實現不錯的系統性能，但是在低頻區域，濾波器組不具有很好的誤差性能。文獻［3-4］利用功率互補條件，通過兩個全通濾波器相加減的形式完成了模擬分解濾波器的設計，實現過程較為繁瑣。而且盡管混疊誤差可達到-100 dB以下，但是失真誤差很難滿足高精度的ADC系統要求。

本文提出一種基于遺傳算法優化設計5階模擬分解濾波器的方法，利用IFFT設計了數字綜合濾波器。通過仿真結果驗證，所設計的混合濾波器組理論上可以滿足24 bits的ADC系統要求。

1 基于功率互補的HFB的基本原理

HFB實現結構原理圖如圖1所示。輸入的信號為帶限信號，由模擬分解濾波器組將輸入信號x(t)按照頻率劃分成M個子頻帶，然后用M片采樣速率為f1=f/M=1/(MT)的ADC進行采樣，其中，f為系統采樣頻率，f1為單片ADC采樣頻率。經過AD采樣后的序列x1［n］通過內插，在序列之間均勻地插入M-1個0值。而綜合濾波器將輸入序列中含有的鏡像頻譜濾除掉，重構信號 y［n］。

在不考慮量化噪聲情況下，輸出y［n］的頻域表示如下［5］

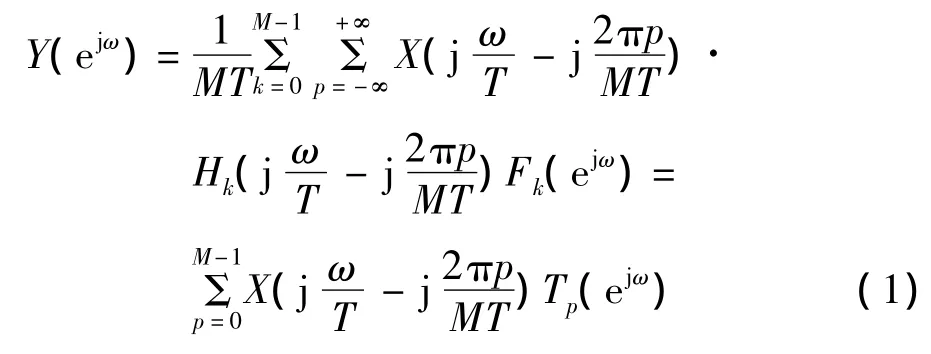
式中:ω=ΩT，ω為數字角頻率，Ω為模擬頻率;

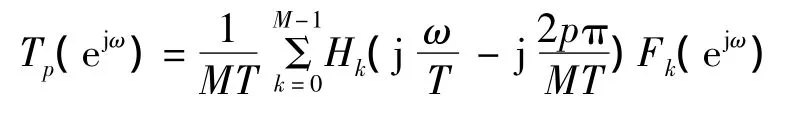
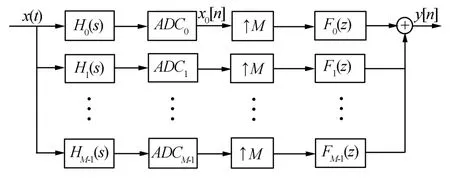
圖1 M通道混合濾波器組的結構原理圖

輸出信號y［n］是由輸入信號經過采樣后頻移后疊加而成的。如果要想獲得理想的信號輸出，則系統的傳輸函數Tp(ejω)必須滿足一定的條件，即

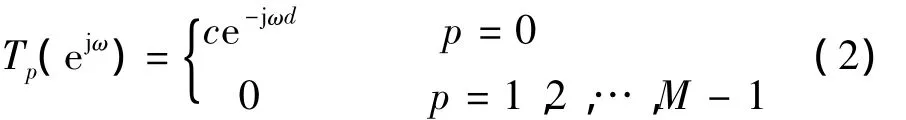
式中:c為尺度常數;d為系統延時。其中，T0(ejω)為系統失真函數，T1(ejω)，T2(ejω)，…，TM-1(ejω)為系統混疊函數。式(2)即為HFB ADC系統的完全重構條件。

1.1 基于功率互補的雙通道混合濾波器組

當M=2時，忽略式(2)中的尺度常數，在不影響整體性能的前提下，為了便于推導分析，將定義采樣周期T=1 s，雙通道的HFB完全重構條件可以表示為［6］

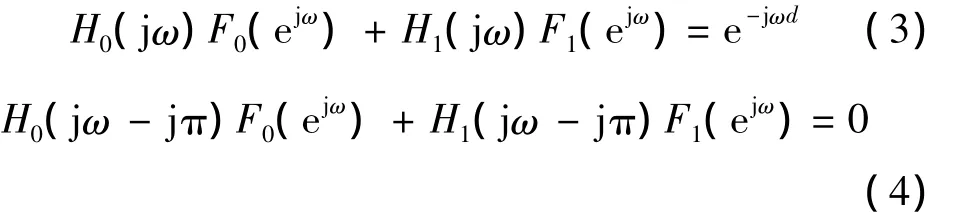
當數字綜合濾波器的頻率響應可以設計成模擬濾波器頻率響應的共軛，則在-π≤ω≤π范圍內滿足

結合式(3)、式(4)可得

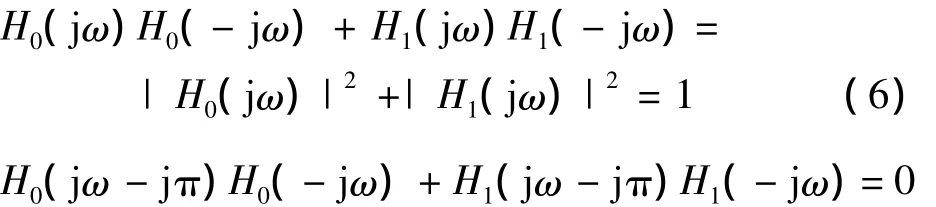
式(6)稱為功率互補條件，滿足此條件的模擬分解濾波器組稱為功率互補型模擬分解濾波器組。

1.2 模擬分解濾波器的設計

根據上節功率互補條件，我們設計兩個模擬濾波器的傳遞函數定義如下［7］

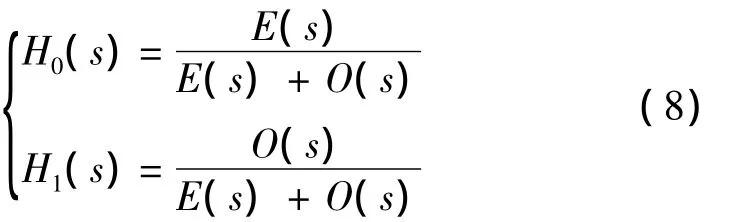
式中:E(s)和O(s)分別是分母多項式D(s){D(s)=的偶次項和奇次項。根據E(s)和O(s)的奇偶性和式(6)、式(7)很容易得到

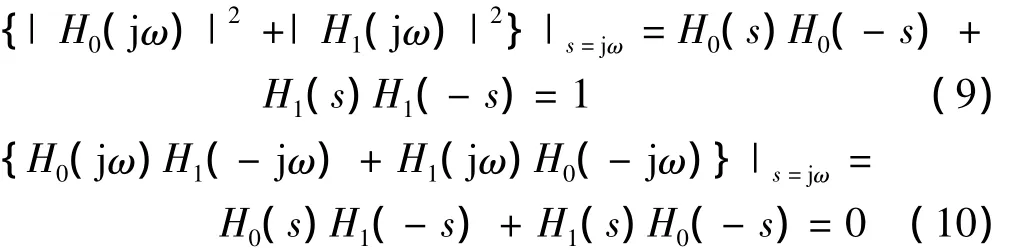
將式(10)、式(7)比較，如果模擬分解濾波器滿足式(13)，則可以滿足完全重構的HFB

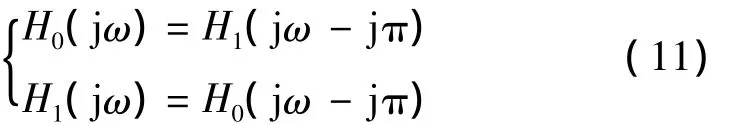
注意到模擬濾波器的頻率響應是關于0頻率點對稱，因此，在實際設計中只需要滿足其中一式即可。

1.3 應用遺傳算法的模擬分解濾波器優化

遺傳算法(Genetic Algorithm，GA)起源于用計算機對自然界生物做的仿真研究，在20世紀中后期，由密歇根大學的Holland教授所在的科研團隊在基于生物遺傳和自然選擇的啟示下提出了一種適合在繁雜系統優化應用的自適應概率技術——遺傳算法［8］。其算法實質是一種并行、全局搜索的方法，可以在搜索過程自行積累有關搜索范圍的經驗，而且能夠自適應地調整搜索方式以得問題的最優解。

本文設計的5階模擬分解濾波器，定義D(s)=s5+as4+bs3+cs2+ds+e。則其中一路模擬分解濾波器的幅頻響應可表示為

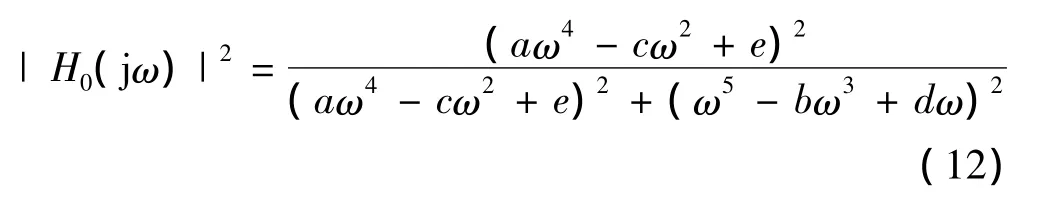
為進一步簡化分解濾波器的傳遞函數，對其模擬濾波器的幅度值做出合理的約束，令濾波器幅頻響應滿足

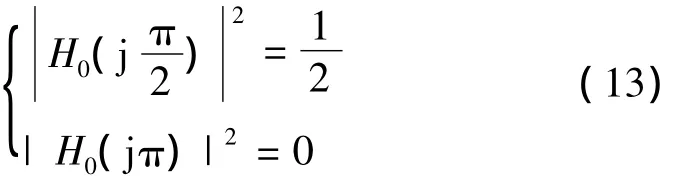
由式(13)可推導出分解濾波器傳遞函數的代數關系，可用 a，b，e來表示 c，d，如式(14)所示

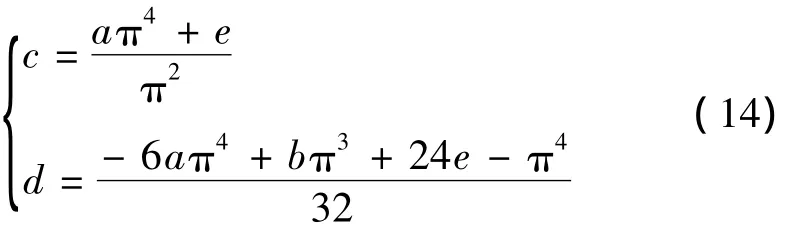
定義

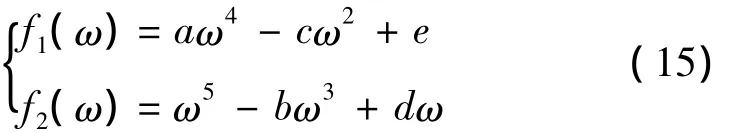
同時，在分解濾波器的優化設計中，應使分解濾波器的幅頻響應滿足在0≤ω≤π為一平滑的曲線。則通過式(15)可表現為:f1(ω)和f2(ω)在0≤ω≤π滿足相應單調性質的要求。通過數學運算簡化，可將要求具體表示為代數不等式，如下所示

式中:Aineq為3×3的矩陣;bineq為3×1的列向量。

在應用遺傳算法優化解決實際問題的時候，首要是初始設置好種群適應度評價函數。根據模擬分解濾波器組的優化設計因素，再根據式(16)的約束濾波器傳遞函數的系數的取值范圍。依據前面所述，可得出模擬分解濾波器的優化目標函數

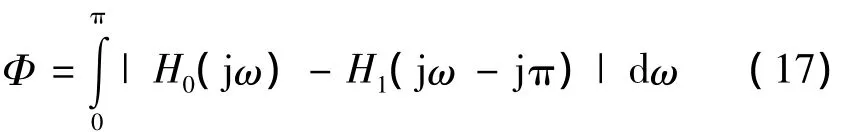
式(17)則為遺傳算法的適應度評價函數，適應度評價函數只存在a、b、e三個獨立變量，而后可多次應用遺傳算法［8］比較得出最優的系數解，最終得到目標函數的極小值4.16E-6。應用遺傳算法優化設計得到的模擬分解濾波器系統傳遞函數的系數為:a=1.947 1，b=69.084 8，c=141.009 8，d=566.845 1，e=4 385.449 8。

兩路分解濾波器的幅頻響應如圖2所示，功率互補結構分解濾波器組的特性可由式(7)表現出來，也可如圖3所示，可以得出基于遺傳算法優化設計的分解濾波器組符合功率互補特性的結論。

圖2 優化設計的5階模擬分解濾波器的幅頻響應

1.4 數字綜合濾波器的設計

對于上節已經優化設計得到的模擬分解濾波器，可以通過式(4)、式(5)得到數字綜合濾波器的頻率響應，利用逆快速傅里葉變換的算法設計N階數字綜合濾波器［9］。在允許一定誤差的情況下對 FIR數字綜合濾波器的長度進行截取，通常采用長度為L的矩形窗，矩形窗表達式如下

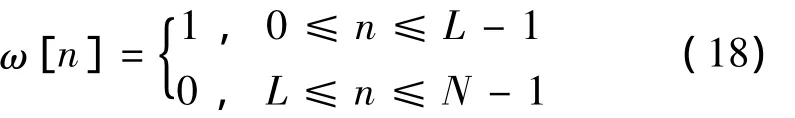
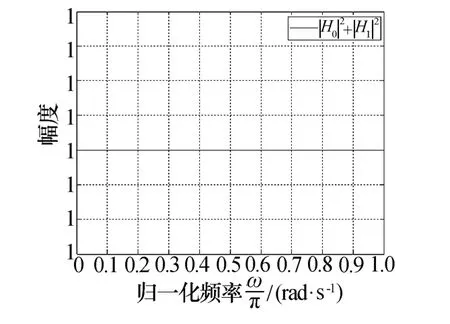
圖3 功率互補結構分解濾波器組特性

那么通過加窗后的數字綜合濾波器的截取系數為

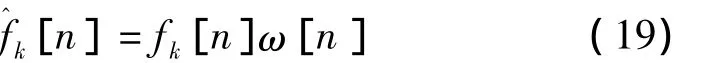
在實際數字濾波器組的優化設計中，還需要對HFB ADC系統中延時進行優化，以得到最佳延時d，使得失真函數逼近純延時，在確定了濾波器的長度L后，HFB ADC系統的最佳延時d為L/2。

2 仿真結果

應用上述優化設計方法，設計了雙通道5階功率互補的模擬分解濾波器，32階的數字綜合濾波器，其中，系統延時，d=16。經過仿真后得到的混合濾波器組的最大失真誤差為4.761 8×1011dB，最大混疊誤差為-154.563 4 dB;平均失真誤差為-9.268 3×10-14dB，平均混疊誤差為-200.537 8 dB。混合濾波器組的失真誤差和混疊誤差幅度如圖4、圖5所示。

圖4 混合濾波器組的失真誤差

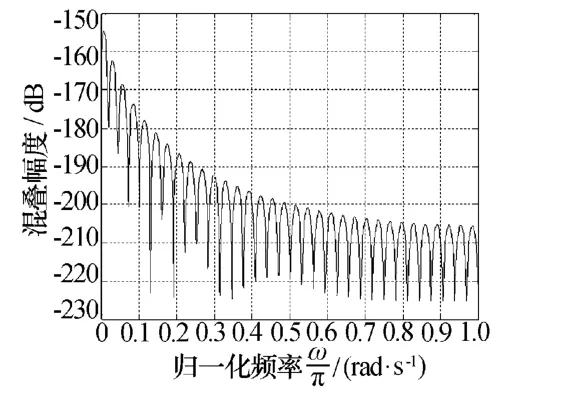
圖5 混合濾波器組的混疊誤差

如圖4、圖5所示，利用遺傳算法優化的功率互補的5階模擬分解濾波器在低頻段也同樣很好的誤差特性。利用本文方法設計的混合濾波器組和現有其他方法設計的混合濾波器組［10］的系統誤差比較如表1所示。

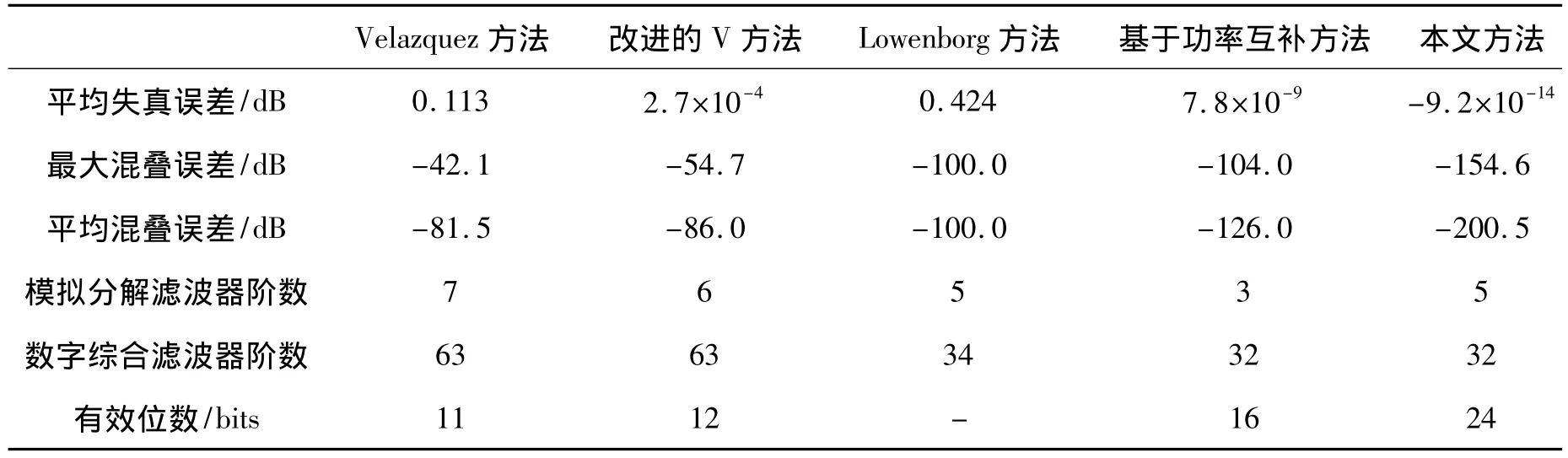
表1 混合濾波器組方法設計的比較

3 結束語

在基于混合濾波器組的數據采集系統中，本文針對模擬濾波器系數的約束條件，提出了基于遺傳算法的優化方法設計來實現高階模擬分解濾波器。實驗仿真表明，相比其他方法，采用本文方法優化設計的混合濾波器組在失真誤差和混疊誤差方面表現出了更好的性能，可以有效提高數據采集系統的采樣精度和采樣速度，可以滿足24 bits的ADC系統的需要，而且整個系統對模擬偏差的敏感度有了很大的降低。

［1］Velazques S R，Nguyen T Q，Broadsto S R.A hybrid filter bank approach to analog-to-digital conversion［C］//Proceedings of the IEEE-SP International Symposium on Time-Frequency and Time-Scale Analysis.［S.l.］:IEEE Press，1994:116-119.

［2］Velazques S R，Nguyen T Q.Design of hybrid filter banks for analog/digital conversion［J］.IEEE Transactions on Signal Processing，1998，46(4):956-967.

［3］Lowenborg P，Johnsson H，Wanhammar L.A design procedure for two-channel mixed analog and digital filter banks for A/D conversion using minimax optimization［C］//IEEE International Conference on Electronic Circuits System.Cyprus:IEEE Press，1999:1189-1192.

［4］Lowenborg P，Johnsson H，Wanhammar L.Two-channel digital and hybrid analog/digital multirate filter banks with very low-complexity analysis or synthesis filter［J］.IEEE Transactions on Ciruits and Systems II:Analog and Digital Signal Processing，2003，50(7):335-367.

［5］Lowenborg P.On the frequency response of M-channel mixed analog and digital maximally decimated filter banks［C］//European Conference on Circuit Theory Design.Stresa:ECCTD Press，1999:545-549.

［6］Song Q，Zhang Z J，Wang W.Design of two-channel hybrid filter banks based on power-complementary structure［C］//2011 IEEE 4th International Symposium on Microwave，Antenna，Propagation，and EMC Technologies for Wireless Communications(MAPE).Beijing，China:IEEE Press，2011:351-354.

［7］劉治宇，林茂六.一種基于功率互補對的混合濾波器組的設計［J］.西安交通大學學報，2005，39(4):389-392，397.Liu Zhiyu，Lin Maoliu.Hybrid filter banks design based on power complementary pair［J］.Journal of Xi'an Jiaotong U-niversity，2005，39(4):389-392，397.

［8］徐 璟，何明浩，冒 燕，等.基于優化算法的雷達輻射源信號識別方法及性能［J］.現代雷達，2014，36(10):33-37，42.Xu Jing，He Minghao，Mao Yan，et al.Radar emitter recognition method based on optimization algorithm and performance［J］.Modern Radar，2014，36(10):33-37，42.

［9］Cheng J，Liu W Y，Ma H.Hybrid filter banks optimization design using total least square solving［C］//2008 International Conference on Microwave and Millimeter Wave Technology.Nanjing，China:IEEE Press，2008:1960-1963.

［10］湯寧生.功率互補性混合濾波器組的設計［D］.成都:電子科技大學，2007.Tang Ningsheng.Hybrid filter banks design based on power complementary［D］.Chengdu:University of Electronic Science and Technology of China，2007.