挖掘隱含信息突破常規(guī)思維
——對一道“90學(xué)時”培訓(xùn)題的解法探析

☉浙江省紹興市柯橋區(qū)平水鎮(zhèn)中　沈岳夫

挖掘隱含信息突破常規(guī)思維
——對一道“90學(xué)時”培訓(xùn)題的解法探析

☉浙江省紹興市柯橋區(qū)平水鎮(zhèn)中沈岳夫

對試題的研究是教師在教學(xué)和復(fù)習(xí)中經(jīng)常做的一件事，通過研究把蘊含其中的數(shù)學(xué)思想方法揭示出來，挖掘出隱含的問題的本質(zhì)屬性，不但可以提高學(xué)生的空間想象能力、邏輯思維能力、分析和解決問題的思維技能，優(yōu)化數(shù)學(xué)的思維品質(zhì)，而且還可以培養(yǎng)學(xué)生探索創(chuàng)新的能力.在2014年10月初中數(shù)學(xué)“90學(xué)時”培訓(xùn)中，筆者領(lǐng)略了臺州市椒江區(qū)舉辦的為期2天的特級教師初中教學(xué)觀摩活動，受益匪淺，其中一道試題給筆者留下深刻的印象，現(xiàn)對其解法進行探究及變式拓展，愿與大家共同分享.

一、題目呈現(xiàn)

如圖1，在△ABC中，AB=AC，∠BAC=90°，AD=CD，AE⊥BD交BD于點E，交BC于點F.

求證：BF=2CF.

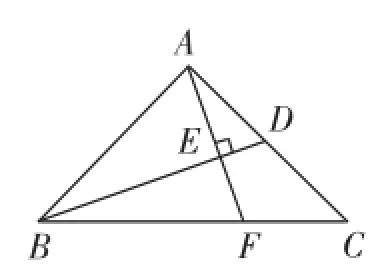
圖1

二、解法探析

本題屬于一道中檔證明題，具有一定的難度，且思維含量較高.根據(jù)題意，解答時應(yīng)先對“母子”相似三角形進行深入探究.如果從邊的角度入手，可設(shè)AD=a，則進而可得DE∶BE=1∶4，DE∶AE=1∶2；如果從三角函數(shù)的角度入手，可得sin∠BAE=等.另外，如果從中點的角度入手，由“中點”可想到中線倍長法、構(gòu)造中位線等；如果注意到∠CAF+∠BAF=90°，且AC=AB，可考慮把△ACF繞點A順時針旋轉(zhuǎn)90°，構(gòu)造出四點共圓，這些都是隱含的信息.據(jù)此我們從不同的角度思考、分析問題，可以探索出多種解題的思路，這對于開闊學(xué)生的思維視野、培養(yǎng)和訓(xùn)練學(xué)生的思維能力，為教師今后的教學(xué)指明導(dǎo)向，都具有極大的教育價值.現(xiàn)列舉如下.

1.利用中點這個特殊條件，構(gòu)造新三角形

圖2

分析：由題意知點D是AC的中點，因此過點C作CH⊥AF，交AF的延長線于點H（如圖2）.易知DE是△AHC的中位線，則HC=2DE，DE∥CH.

說明：還可以如圖3、圖4、圖5所示添輔助線，圖3用“中線倍長”的方法，先證△ADH≌△CDB，再證△AEH∽△FEB，然后通過線段間的數(shù)量關(guān)系證明；圖4用“遇中點，構(gòu)全等”的方法，先證△ADE≌△CDH，再由△BEF∽△BHC，得到線段間的比例關(guān)系；圖5用“遇中點，構(gòu)相似”的方法，顯然△ADH∽△ACF，△DHE∽△BFE，再由探析中的邊之間的關(guān)系證明.綜觀這幾種方法，其本質(zhì)都是通過“中點”構(gòu)造出一個新三角形，將分散的條件通過全等或相似得到等量關(guān)系，進而問題得以解決.

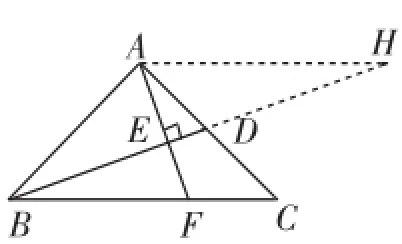
圖3

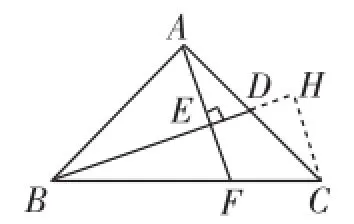
圖4

圖5

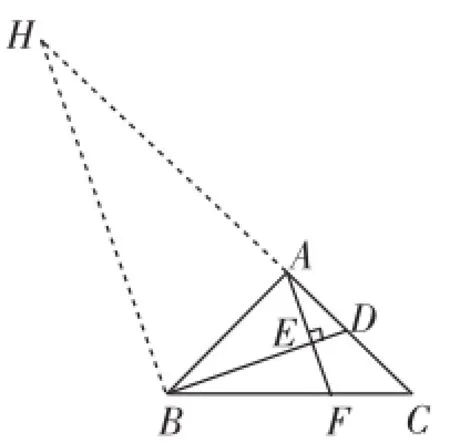
圖6

2.利用平行線截得的線段成比例，構(gòu)造平行線

分析：由于AF⊥BD，所以過點B作BH∥AF，交CA的延長線于點H（如圖6）.則△DAE∽△DHB.由探析知

說明：本解法實際上是構(gòu)造了“雙A”型的相似三角形，即△DAE∽△DHB和△CAF∽△CHB，然后通過DE∶BE=1∶4的橋梁加以轉(zhuǎn)化，進而問題得以解決.當(dāng)然，添平行線的方法還有很多種，有興趣的讀者不妨試試.

3.利用∠α＋∠β=90°，且具有共點相等線段，通過旋轉(zhuǎn)構(gòu)造四點共圓

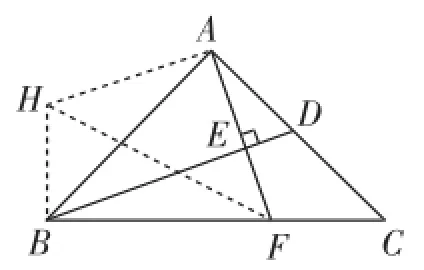
圖7

分析：因為∠CAF＋∠BAF= 90°，且AC=AB，可考慮把△ACF繞點A順時針旋轉(zhuǎn)90°（如圖7）.易知△ACF≌△ABH，CF=BH，∠HBA=∠FCA=45°，所以∠HBF=90°，∠HAF=∠HAB＋∠BAF=90°，所以A、H、B、F四點共圓.

連接HF，則∠BFH=∠BAH.又∠BAH=∠FAC， tan∠CAF=，所以tan∠BFH=，即BF=2CF成立.

說明：本解法的關(guān)鍵是注意到∠CAF＋∠BAF=90°，且AC=AB，可考慮把△ACF繞點A順時針旋轉(zhuǎn)90°，然后挖掘出∠HBF=∠HAF=90°，這樣就可以利用“四點共圓”及“同弧所對圓周角相等”求解，顯得簡捷、明了.

4.利用“數(shù)”“形”互通，構(gòu)造直角坐標(biāo)系

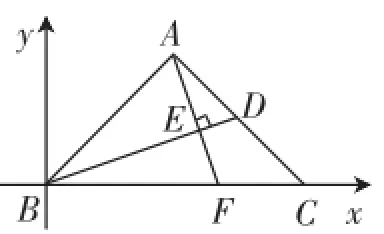
圖8

分析：如圖8，以B為坐標(biāo)原點，BC所在直線為x軸建立直角坐標(biāo)系.為方便計算，設(shè)點C的坐標(biāo)為（4a，0）（a＞0）.易得點A（2a，2a），點D（3a，a）.接下來，我們先求出直線BD的解析式y(tǒng)=x.因為AF⊥BD，所以kBD· kAF=-1.于是可得直線AF的解析式y(tǒng)=-3x+8a，則點F的坐標(biāo)為進而可求得即BF=2CF成立.

說明：坐標(biāo)法的基本思想在于幾何問題代數(shù)化，圖形性質(zhì)坐標(biāo)化，把有關(guān)圖形的問題“翻譯”成相應(yīng)的代數(shù)問題，然后用代數(shù)知識進行演算、論證，最后把所得的結(jié)果“翻譯”成幾何圖形的性質(zhì)，以達到證明幾何問題的目的.本解法主要是根據(jù)條件中有特殊的點（如中點）、特殊的位置（如AF⊥BD）或特殊的圖形時（如等腰直角三角形），通過建立適當(dāng)?shù)闹苯幼鴺?biāo)系，可以將某些幾何求值問題、證明問題全部轉(zhuǎn)化或部分轉(zhuǎn)化為代數(shù)問題加以解決（有時較之其他的方法更為簡潔）.

分析：我們先看一個熟悉的圖形（如圖9）：四邊形ABGH、四邊形BCFG、四邊形CDEF都是正方形.易證∠BCH＋∠BDH=45°，顯然tan∠BCH=，tan∠BDH=.

基于這種思路，過點A作AH⊥BC，交BC于點H（如圖10），則AH平分∠BAC，所以∠HAF＋∠CAF=45°.因為tan∠CAF=tan∠DAE=，所以tan∠HAF==，進而證得BF=2CF成立.

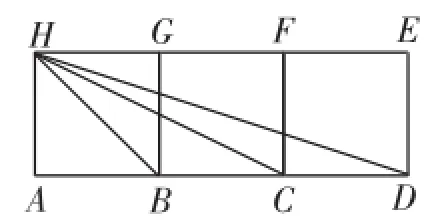
圖9

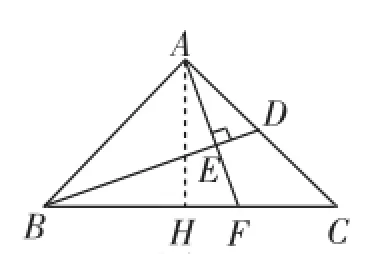
圖10

6.利用面積，巧妙化解線段的數(shù)量關(guān)系

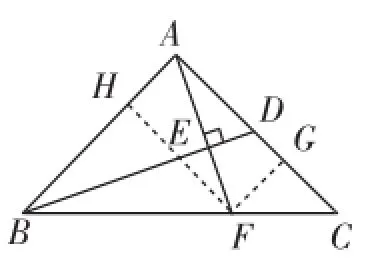
圖11

分析：如果從面積角度出發(fā)，不妨設(shè)點A到BC邊的距離為h，再過點F作FG⊥AC，F(xiàn)H⊥AB，垂足分別為點G、點H（如圖11）.則S=BF·

△ABF兩式相比，可得即 BF=2CF成立.

說明：本解法利用了“等積轉(zhuǎn)化”的方法求解，其實本題還可用S=absin∠α這個公式進行解答，即S=

△ABFBF·h=AB·AF·sin∠BAF，S=CF·h=AC·△ACFAF·sin∠CAF，兩式相比，得由前面探析知所以=2，進而證得.

三、變式拓展

著名數(shù)學(xué)教育家波利亞曾說過：“好問題同某種蘑菇有些相像，它們都成堆地生長，找到一個以后，你應(yīng)當(dāng)在周圍找找，很可能附近就有好幾個.”因此在解決問題之后，還要通過變化對象的非本質(zhì)屬性，來提高對數(shù)學(xué)知識的典型運用和遷移運用能力，豐富對數(shù)學(xué)基本思想方法的體會，提高對問題結(jié)構(gòu)信息的識別能力和數(shù)學(xué)知識的合理選擇能力，提高分析問題和解決問題的能力.總之，變式探究對提高自身的解題能力和教學(xué)水平，會有十分重要的作用.

變式1：如圖12，在Rt△ABC中，∠ABC=90°，點D為線段BC上的動點（點D不與B、C重合），直線BE⊥AD于點E，交直線AC于點F.若=n，請?zhí)骄康闹担ㄓ煤琻的式子表示）.

圖12

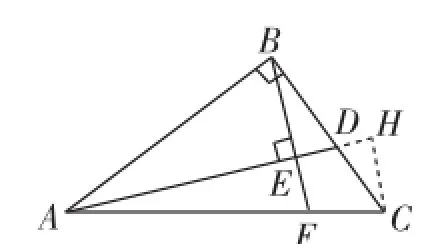
圖13

解析：如圖13，過點C作CH⊥AD交AD于點H.易證△BDE∽△CDH，則所以，則AB=nBC，BD=nDC，ED=nHD.進而得BC=（n+1）DC，EH=

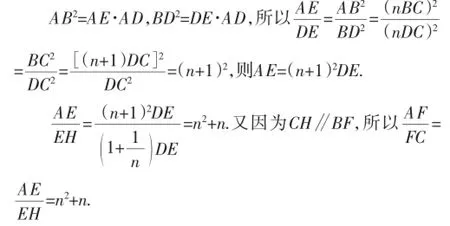
變式2：如圖14，在Rt△ABC中，∠ABC=90°，點D為線段BC的延長線上的動點（點D不與B、C重合），直線BE⊥AD于點E，交直線AC于點F.若=n，請?zhí)骄康闹担ㄓ煤琻的式子表示）.

圖14

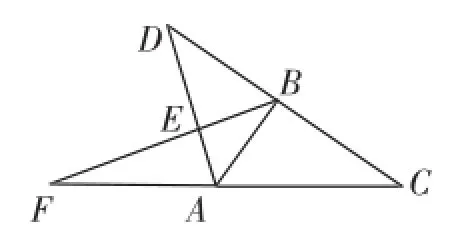
圖15

變式3：如圖15，在Rt△ABC中，∠ABC=90°，點D為線段CB的延長線上的動點（點D不與B、C重合），直線BE⊥AD于點E，交直線AC于點F.若=n，請?zhí)骄康闹担ㄓ煤琻的式子表示）.

參考答案：

說明：變式1、變式2、變式3是對原題進行了一般性的探究，揭示了命題中條件與隱含條件、結(jié)論的內(nèi)在聯(lián)系，體現(xiàn)了從“特殊”到“一般”的數(shù)學(xué)規(guī)律，也是對上述眾法選優(yōu)的內(nèi)化與升華.可見，在平時教學(xué)中，我們應(yīng)該多對一些已有的習(xí)題進行有效的變式，形成一個有層次、有梯度的題組或題鏈，引導(dǎo)學(xué)生從“變”的現(xiàn)象中發(fā)現(xiàn)“不變”的本質(zhì)，從而達到“以不變應(yīng)萬變”的目的.

綜上可以看出，每個優(yōu)秀的數(shù)學(xué)題目中都包含著大量基礎(chǔ)知識、基本方法與技巧、策略，都蘊含著數(shù)學(xué)的方法、思想等本質(zhì).因此對于一些“典型”的“熟題”，教學(xué)中應(yīng)該采用“一題多變”的基本方法，力爭讓學(xué)生學(xué)透.因為是“熟題”，解決此類題目可以起到“溫故而知新”的效果；因為是“典型”，題目必定包含有不同的解決方法，方法越多，對顯性知識技能的訓(xùn)練就越到位.解決此類題目可以達到“知識與方法”同步提高的效果.在一題多解教學(xué)中，首先要注重通性、通法，其次才是研究最優(yōu)解法，最后要對研究的問題從知識技能、解題規(guī)律、思想方法等角度進行歸納、總結(jié)、反思，幫助學(xué)生積累解題經(jīng)驗，進而增加學(xué)生思維的寬度，達到解題效果的最大化.

1.沈岳夫.注重組題設(shè)計提升思維品質(zhì)［J］.中學(xué)數(shù)學(xué)教學(xué)參考（中），2012（6）.

2.徐強.一道中考題的解法、演變與推廣［J］.中學(xué)數(shù)學(xué)（下），2014（11）.

3.徐成祥.活用數(shù)學(xué)知識抽象數(shù)學(xué)模型——以2012年深圳市中考數(shù)學(xué)第16題為例［J］.中學(xué)數(shù)學(xué)教學(xué)參考（中），2014（10）.