適用于臨近空間飛行器大變形的動網格策略*

柳兆偉，侯中喜，陳立立

適用于臨近空間飛行器大變形的動網格策略*

柳兆偉，侯中喜，陳立立

(國防科技大學 航天科學與工程學院， 湖南 長沙 410073)

對于超大展弦比構型的低速臨近空間飛行器而言，由于其在飛行過程中結構變形非常顯著，因此基于計算流體力學的分析方法對于動網格提出了非常高的要求。為此，提出了一種適用于邊界大變形的動網格策略，該種動網格基于映射的思想，將邊界網格的位置變化以某種權重反映到流場網格，并更新網格節點位置。選取距離倒數的n次方作為權重，研究不同的權重指數n對網格變形的影響規律，然后開展了二維與三維動網格實例分析。結果表明，這種動網格方法能夠很好地適用于大變形的情形，并能很好地保證變形后的網格質量。

動網格；大變形；變形策略

(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)

在軍用和民用領域巨大需求的牽引下，高空長航時(High Altitude Long Endurance,HALE)飛行器得到快速的發展，特別的以“太陽神”[1]“微風”“陽光動力”等為代表的一系列太陽能飛機的發展，大大促進了該技術的提升。如圖1所示，展示了幾種高空長航時太陽能飛行器。為了實現高空長航時這一目標，該類型飛行器結構面密度通常較低，由此導致剛度明顯不足，在飛行過程中受到氣動載荷時，結構變形非常顯著，同時結構變形又使得氣動性能發生改變，因而結構與氣動出現較強耦合。

圖1 高空長航時大展弦比飛行器Fig1 HALE high-aspect-ratio aircrafts

近年來，基于計算流體力學的流固耦合分析方法得到快速的發展與廣泛的應用[2-6]。這種方法要求結構和氣動兩個學科獨立建模，并采用交錯求解的方式進行計算。流體計算中一般采用基于空間位置的Euler網格，因而在耦合過程中，流體網格需要根據結構邊界的移動而變化。特別的，對于超大展弦比構型的低速臨近空間飛行器而言，在飛行過程中其結構變形非常顯著，因而需要發展適用于大變形的動網格策略。

目前，動網格主要的實現方法可分為兩大類[7]：網格重構和網格變形。網格重構技術基于超限插值(TransFinite Interpolation,TFI)技術，在每次邊界變化時，重新劃分網格，這種方法計算量較大，效率較低。另一種常用的動網格方式是網格變形技術，該方法將網格作為彈簧或彈性體來處理，并根據靜力平衡計算得到新的網格點位置。但是彈簧算法在處理大變形或者較密的網格時，常會出現交叉而產生負體積網格，導致網格更新失敗。近年來， Liu[7]等采用Delaunay背景網格的變形方法實現網格更新，這種動網格方法能夠適應于大變形的情形，特別是對于大的位移情況，然而當有大的扭轉變形時，將會出現Delaunay圖的交叉，而導致網格更新失敗。

本文提出一種基于映射的網格變形策略，其基本思想是：不改變網格的拓撲結構，將邊界的變形量按照一定的權重映射到流域中的網格點，從而確定流場中網格的位移。選取待移動網格節點到邊界上點的距離倒數的n次方作為權重，其出發點是，要調整的網格點到邊界網格點距離越近，受到邊界網格點的影響也越大，通過調整指數n可以調整影響的擴散范圍。

1 網格變形

1.1 網格變形方法

網格更新方法可分為四個步驟：

第一步，計算網格節點至邊界點的距離。設計算域為D，節點個數為p，邊界區域為B，節點個數為q，其中D包括B。則計算域D內任意一點i到邊界B上一點j的距離為dij。且：

(1)

第二步，計算邊界網格點位移量。按照一定的要求變化邊界區域B，得到網格邊界B上任意一點j的位移量：

(2)

第三步，選取距離的倒數的n次方作為網格更新的權重，計算網格位移量。對于區域D內的任意一點i而言，根據選取的n，按照映射關系，可確定其位移量為：

(3)

有一點需要特別注意的是，當點為邊界上的點時，其位移變化則不受到其他點的影響。即若dij=0，則該點的位移為：

Δri=Δrj

(4)

第四步，根據上述位移量，重新確定網格點坐標。對于計算域D內的任意一點i，其新的坐標位置為：

(5)

1.2 網格更新的實現

整個網格變形的思想是：將邊界的運動按照某種權重映射到每個網格點上。因而在實現過程中，可分為內外層兩個循環，內層是計算邊界位移對于某一網格節點的權重，得到網格點位移；外層則是循環所有網格節點，更新坐標位置。

具體過程可寫為如下的偽代碼：

for i=1：number of domain points

{

Δrsum=0;

dback=0;

for j=1：number of boundary points

{

更新邊界點j坐標，得到Δrj;

計算該點到邊界點j的距離dij;

if dij= 0

{

Δrsum=Δrj；

dback=1；

break；

}

}

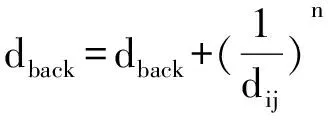
end

}

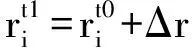
end

2 權重指數的影響

選取(1/d)n作為權重，出發點是：要調整的網格點到邊界網格點距離越近，受到邊界網格點的影響也越大，通過調整指數n可以調整影響的擴散范圍。

下面結合二維大變形的動網格算例，通過觀察不同的n值得到網格的差異，研究n的取值對于網格變形的影響規律。設原始網格如圖2所示，將大變形分為內部物體的扭轉變形和平移變形兩種情況。則不同的n值對應的變形網格如圖3和圖4所示。

圖2 原始網格Fig.2 The initial mesh

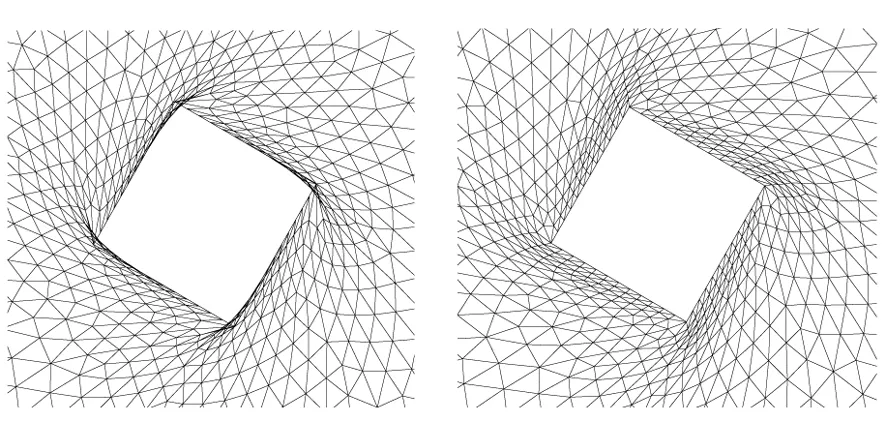
(a)n=2時網格(a) The mesh while n=2(b) n=4時的網格(b) The mesh while n=4

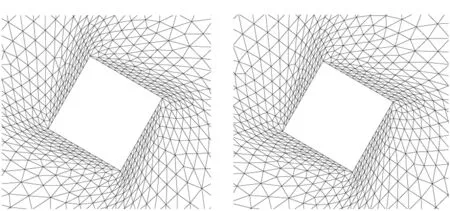
(c) n=6的網格(c) The mesh while n=6(d) n=8的網格(d) The mesh while n=8圖3 物體轉動時不同n值對應的物體周圍網格Fig.3 The mesh versus different n with torsion deformation

對于純扭轉位移而言，假設扭轉角度為60°。當n=2時變形網格如圖3(a)所示，可以看出，外層網格變形較小，而內層網格扭曲較為嚴重，出現負體積網格。而隨著n值的增大，內層網格對于變形壁面的跟隨性也越好，外層網格扭轉幅度增大，這也意味著壁面網格質量更好，如圖3(c)、(d)。

平移變形情況下，不同的n對應的網格變形結果如圖4所示。可以看出，n取值越大，變形物體周圍內層網格的變形越小，邊界的平移變形被傳播到更遠的外層網格區域。然而當外層網格需要承受非常大的變形時，則可能會出現交叉而使得網格更新失敗。

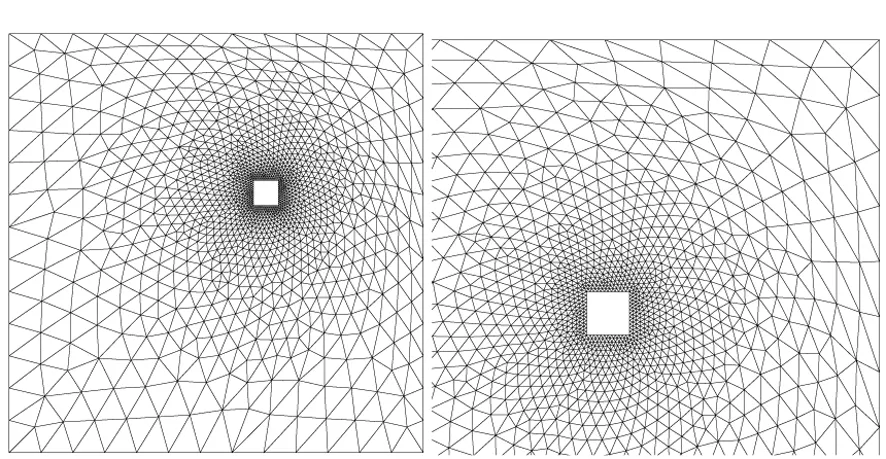
(a) n=2時網格(a) The mesh while n=2

(b) n=3時網格(b) The mesh while n=3

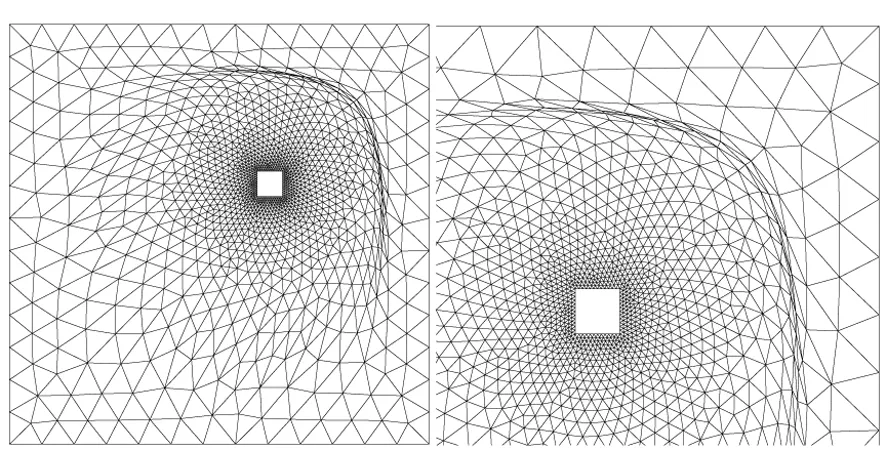
(c) n=4時網格(c) The mesh while n=4圖4 物體平移時不同n值對應的物體周圍網格 Fig.4 The mesh versus different n with large displacement

通過設定不同的n值，觀察網格變形的規律，可以發現：n值越大，運動邊界周圍網格的剛性越強，對于扭轉變形的適應能力也越強；而對于平移變形而言，當n較大時，運動壁面的位移傳播到外層網格中，而使得遠離壁面的區域的網格變形較大。綜上，n值的選取可采取如下的原則：一般n取2～6，且當扭轉變形較大時，可取相對較大的n值，而當平移較大時，可適當取較小的n值。同時，對于初始網格本身而言，更大的流域以及較大的外部網格尺寸也會增大網格變形的空間，增強變形能力。

3 網格變形實例

下面結合不同的大變形動網格實例，分析變形后網格的質量。算例包括二維翼型的旋轉與平移、二維不規則變形、三維球體的變形與移動以及三維機翼大幅縱向變形。

3.1 二維翼型網格變形

在飛行器的性能分析中，對典型截面的非線性氣動彈性研究具有重要的意義。基于計算流體力學的分析手段能夠非常好地預測流體的分離等非線性現象等。下面考慮如下的翼型C形結構化網格，如圖5所示，當翼型具有大的平移和扭轉時，根據上述方法得到的網格分別如圖6、圖7、圖8所示。

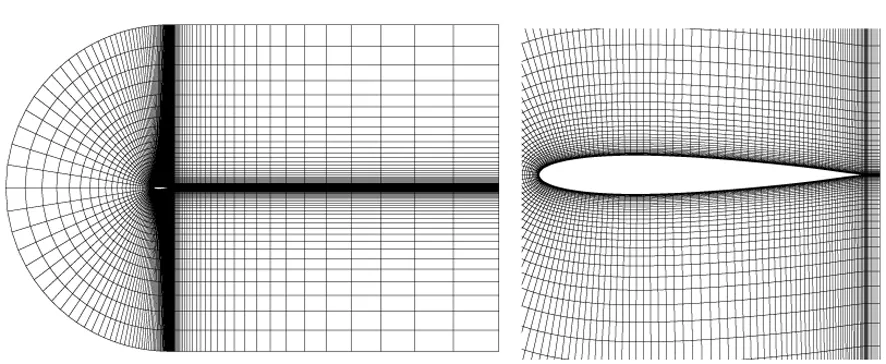
圖5 翼型原始網格Fig.5 The initial mesh of airfoil

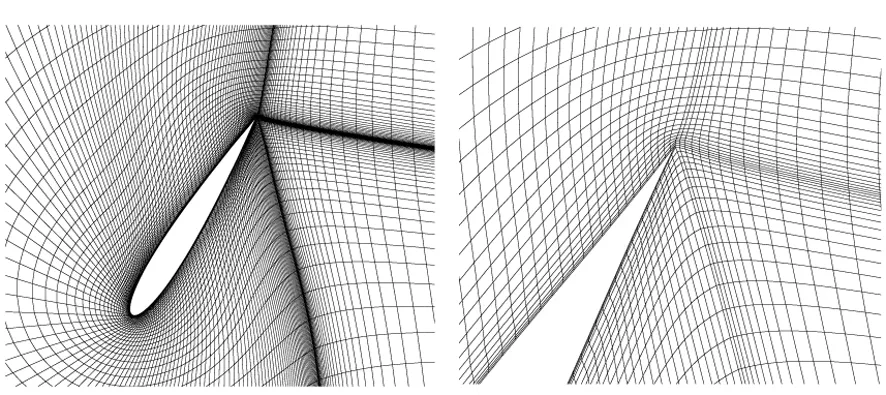
圖6 翼型扭轉60°網格變形圖(n=4)Fig.6 The mesh with 60° torsion deformation (n=4)

圖7 大范圍平移后網格變形圖(n=2)Fig.7 The mesh with large displacement (n=2)

圖8 翼型同時扭轉和平移后的變形網格(n=2)Fig.8 The mesh with large displacement and torsion (n=2)

由上述變形后的網格可以看出，在翼型出現非常大的扭轉或者平移時，可以通過調節權重指數n的值，將翼型邊界的位移很好的傳播到大尺寸的網格中，從而保證良好的壁面邊界層網格質量。

3.2 二維壁面不規則變形

在飛行器外形設計及翼型優化等方面，可能會涉及到曲線或曲面的不規則變形等情形。針對如圖9所示的網格區域，假設內部邊界的上表面出現正弦波動變形，而下表面出現鋸齒狀變形。

圖9 初始網格以及邊界變化Fig.9 The initial mesh and the deformation of the wall

觀察上述邊界變化，可知這種變形主要是小區域內的大扭轉變形，此時我們需要保證靠近壁面的網格質量，并避免出現過度扭曲而導致網格更新失敗，根據上面n值的選擇原則，應取較大的n值，以保證壁面附近網格的剛度，此處取n=6，如圖10所示為更新后的網格。

圖10 更新后的網格(n=6)Fig.10 The mesh after deformation (n=6)

對于上表面而言，邊界扭曲較為嚴重，網格受到一定的拉伸或壓縮；而對于下表面而言，網格變形后依然較為均勻；而側面由于未變形，網格變化很小。可以看出，當壁面出現不規則變形時，采用這種動網格方法，通過選取合適的n值，能夠較好地保證變形后的網格質量。

3.3 三維球體網格變形

對于臨近空間球形或者艇形的浮空器而言，當內外壓差變化或者受到外界氣流干擾時，其結構會出現大幅變形。下面以三維球體的外流場計算網格為例，驗證上述動網格方法。

球體的原始網格如圖11所示，在球體的周圍網格較密，而外層網格較為稀疏。圖12(a)、(b)、(c)分別為球體發生平移、變形、扭轉后的變形網格結果。可以看出，采用上述網格變形方法，能夠獲得高質量的網格。

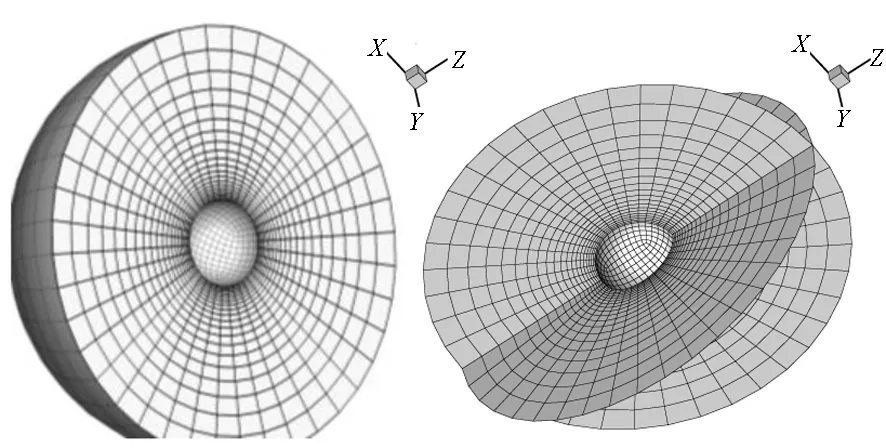
圖11 球體原始網格Fig.11 The initial mesh of sphere

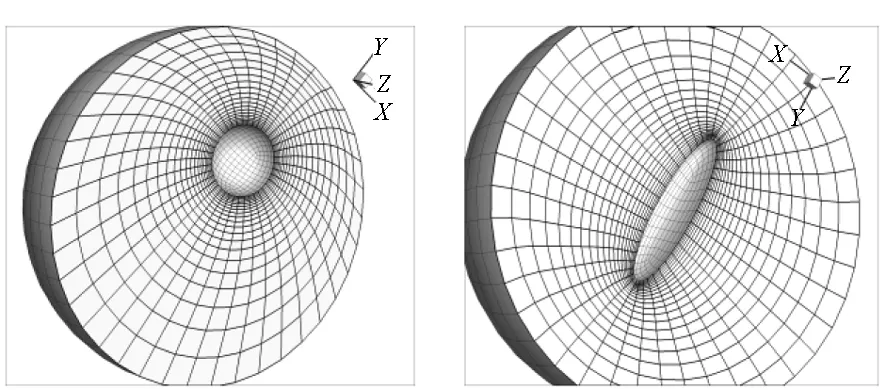
(c) 內部球體旋轉60°網格圖(n=6)(c) The mesh with 60° rotation of inside sphere (n=6)圖12 不同變形情形下的網格結果Fig.12 The mesh with different deformation case

3.4 三維機翼網格變形

對于臨近空間大展弦比長航時太陽能飛機而言，為了降低能源消耗，其重量通常相對較小，由此導致結構剛度不足，在飛行過程中常常會出現非常大的縱向變形。下面假定一定幅度的機翼縱向變形，查看上述動網格方法對于變形的適應性及變形后網格的效果。

在機翼的氣動力計算中，通常機翼周圍的網格較密(以提高計算精度)，而遠離機翼壁面的區域網格非常稀疏，如圖13所示。

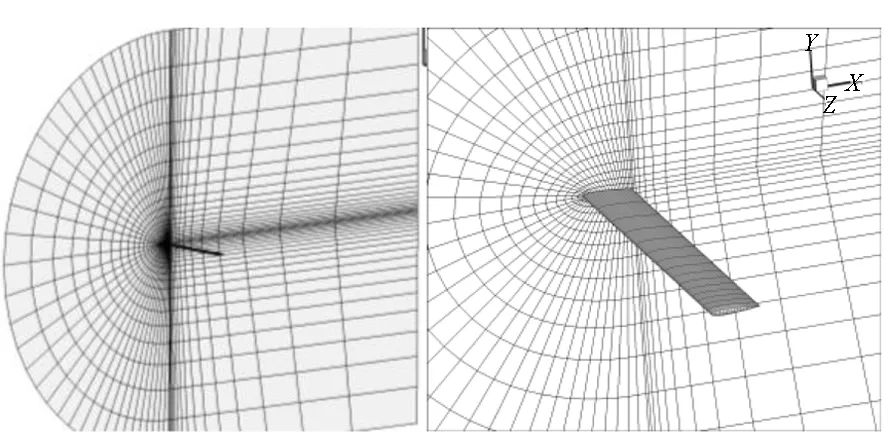
圖13 機翼原始網格Fig.13 The initial mesh of wing

希望在網格變形后，依然能夠保持良好的壁面網格質量。假設機翼的翼尖縱向變形量達到展長的50%，如圖14所示。采用本文的網格變形策略得到變形后的網格如圖15、圖16所示。可以看出，大的縱向變形出現后，機翼壁面周圍網格質量依然較好，而變形被傳播到遠離機翼壁面的外層大尺度網格中，這對氣動計算而言非常重要。

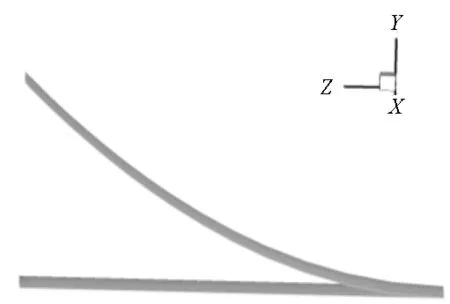
圖14 機翼縱向變形Fig.14 The longitudinal deformation of the wing

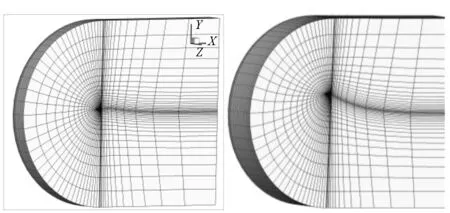
圖15 不同截面上的網格(n=4)Fig.15 The mesh at different sections (n=4)

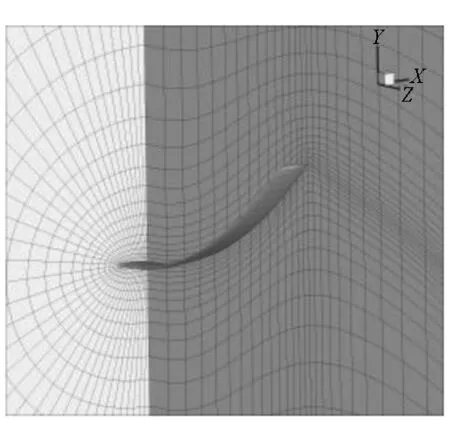
圖16 變形后的機翼網格(n=4)Fig16 The wing mesh after deformation (n=4)

4 結論

基于映射的思想，提出一種網格變形策略，其基本思想是：將邊界的變形量以某種權重反映到流場區域網格中。文中以(1/d)n為權重，并結合二維算例研究了指數n對于網格變形的影響，結果表明，指數n值越大，邊界周圍網格的剛性越強，而變形更容易被傳播到遠離邊界的區域。n值的選取可采取如下的原則：一般取2～6，當扭轉變形較大時，可取相對較大的n值，而當平移較大時，可適當取較小的n值。

References)

[1]NollTE,BrownJM,Perez-DavisME,etal.Investigationoftheheliosprototypeaircraftmishap,volumeI:mishapreport[R].USA:NationalOceanicandAtmosphericAdministration, 2004.

[2]YangGW,ChenDW,CuiK.Responsesurfacetechniqueforstaticaeroelasticoptimizationonahigh-aspect-ratiowing[J].JournalofAircraft, 2009, 46(4): 1444-1450.

[3]PalaciosR,CesnikCES.Staticnonlinearaeroelasticityofflexibleslenderwingsincompressibleflow[C]//Proceedingsof46thAIAA/ASME/ASCE/AHS/ASCStructures,StructuralDynamicsandMaterialsConference, 2005.

[4]HallissyBP,CesnikCES.High-fidelityaeroelasticanalysisofveryflexibleaircraft[C]//Proceedingsof52ndAIAA/ASME/ASCE/AHS/ASCStructures,StructuralDynamicsandMaterialsConference, 2011.

[5]GarciaJA.Numericalinvestigationofnonlinearaeroelasticeffectsonflexiblehigh-aspect-ratiowings[J].JournalofAircraft, 2005, 42(4): 1025-1036.

[6]CarnieG,QinN.Fluid-structureinteractionofHALEwingconfigurationwithanefficientmovinggridmethod[C]//Proceedingsof46thAIAAAerospaceSciencesMeetingandExhibit, 2008.

[7]LiuXQ,QinN,XiaH.FastdynamicgriddeformationbasedonDelaunaygraphmapping[J].JournalofComputationalPhysics, 2006, 211(2): 405-423.

Moving mesh strategy for large deformation of near-space aircrafts

LIU Zhaowei, HOU Zhongxi，CHEN Lili

The high-aspect-ratio low-speed near-space aircrafts may undergo very large deformation during flight, so a high demand of moving mesh is required for the analysis method based on computational fluid dynamics. To this end, a moving mesh strategy for large deformation of the boundary was presented. The strategy which is based on the mapping interpolation method reflects the displacement of boundary mesh to flow field mesh using a certain kind of weight and then updates the position of mesh nodes. Inverse distance’snth-power was chosen as the weighting factor and the influence of different weight indexnon the mesh deformation was studied, then the analysis of some two-dimensional and three-dimensional moving mesh cases was carried out. The results suggest that this method is capable of handling the large deformation and ensuring the quality of deformed mesh.

moving mesh; large deformation; deformation strategy

2015-04-08

國家高分重大專項資助項目(GFZX04060103)

柳兆偉(1988—)，男，安徽臨泉人，博士研究生，E-mail：liuzhaowei@nudt.edu.cn；侯中喜(通信作者)，男，教授，博士，博士生導師，E-mail：hzx@nudt.edu.cn

10.11887/j.cn.201504004

http://journal.nudt.edu.cn

V211.3

A

1001-2486(2015)04-019-06