以應用為導向的工科“線性代數”教學模式改革探索
黃利國 高麗


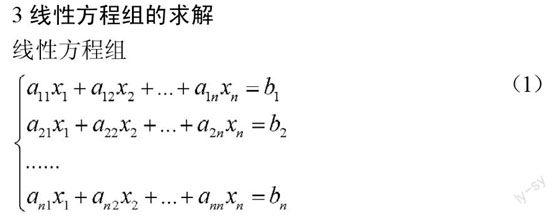
摘 要 隨著科學技術的發展線性方程組有了廣泛應用,對于生活中的許多問題都可以用線性方程組來解決。本文結合在“線性代數”教學中對相關知識點的認識,通過對矩陣相關知識的剖析,探討了矩陣與行列式、向量、向量組線性相關性、線性方程組的解的關系,以方便講課時將相關知識點對照,加深學生對相應知識點的理解。最后,給出了求解“線性代數”中相關問題的Matlab命令。
關鍵詞 系數矩陣 行列式 向量 線性方程組 Matlab
中圖分類號:G424 文獻標識碼:A DOI:10.16400/j.cnki.kjdkz.2015.10.060
The Application-oriented Exploration and Reform of Teaching
Mode for the Engineering Students in "Linear Algebra"
HUANG Liguo, GAO Li
(Mathematics Department, Binzhou University, Binzhou, Shandong 256603)
Abstract With the development of science and technology, linear equations have been widely used. It can be used to solve many problem in the life. In the teaching of "Linear Algebra", we analyze the relevant knowledge of Matrix, and the relationship between Matrix and Determinant, Vector, the linear correlation of Vector Group and the solution of Linear Equations. So that, we can contrast the corresponding knowledge in teaching, which can deepen students' understanding. At last, some matlab command is shown for solving the problems in "Linear Algebra".
Key words Coefficient Matrix; determinant; vector; Linear Equations; Matlab
對于“線性代數”的學習,貫穿始終的一個概念就是矩陣,①②學生對矩陣的理解和相關知識的掌握,直接影響著其對這門課的掌握,特別是在工程領域中,借助于Matlab軟件③④對相關內容進行講解,更有助于學生對知識點的理解,并且對學生參加建模比賽和以后的工作也能起到事半功倍的作用。⑤為了使學生對線性代數有一個系統的掌握,下面對矩陣與線性方程組的相關內容進行總結,并結合Matlab軟件舉例說明其方便和實用之處。
1 矩陣的相關概念與記號
實數的全體用表示;實維向量的全體用表示;實矩陣的全體用表示。對于給定的矩陣,我們用,和分別表示矩陣的共軛、轉置和伴隨矩陣;用()表示的秩;用表示中所有秩為的矩陣的全體。如果,則稱為階方陣;對于給定的階方陣,我們用()和()分別表示的行列式和跡;如果()≠0,就稱是非奇異的。對于非奇異矩陣,用表示的逆矩陣。維向量也可以看成矩陣的特殊情形。維行向量就是1拙卣螅邢蛄烤褪莯?矩陣。可用大寫的拉丁字母…或者()()…來代表矩陣。為了指明所討論的矩陣的行數和列數,可以把拙卣笮闖?…,或者,…
2 矩陣的運算
矩陣計算主要用于:
(1)求線性方程組的解,即給定拙卣蠛臀邢蛄浚笪邢蛄渴溝?= ;最特殊地,為階非奇異方陣,此時方程組 = 的解是唯一的;
(2)計算一個矩陣的特征值和特征向量,即給定一個方陣,求它的全部或部分特征值,或者相應的特征向量。
設,如果存在和滿足 = ,≠0,則稱是的特征值,是屬于的特征向量,的特征值的全體記作()。容易驗證,()的充分必要條件是() = 0。因此,多項式() = ()稱作的特征多項式。
顯然有() = (),因此,() = ()。如果有個互不相同的特征值,,…,,它們作為()的根的重數分別是(),(),…,(),即() = ,≠(≠),() = ,則稱()為的重數;一般將重數為1的特征值稱作單特征值。
如果滿足 = ,其中是非奇異的階方陣,則稱與相似。容易驗證,如果與相似,則() = ()。因此,相似矩陣有相同的特征多項式,從而它們有相同的特征值。
3 線性方程組的求解
線性方程組
(1)
是人們熟知的計算模型,它在科學與工程計算中扮演著極其重要的角色。線性方程組有廣泛應用,熟知的線性規劃問題即討論解有一定約束條件的線性方程組問題。根據實際情況可將線性方程組分為三類,適定方程組、不定方程組和超定方程組。當方程組中實際的方程數等于未知數個數時,這一類方程組稱為適定方程組;如果其系數矩陣可逆,適定方程組有唯一的解,求解適定方程組的方法有克萊姆方法、消元法、矩陣分解法、迭代法等;當方程組中實際的方程數少于未知數個數時,這一類方程組稱為不定方程組;當系數矩陣的秩等于增廣矩陣的秩時,不定方程組有無窮多組解。根據線性代數的理論和方法,可求得方程組的通解。
線性代數中介紹過行列式解法的Gramer法則。眾所周知,如果方程組(1)的系數行列式()的值異于0,則它有唯一解,運用Gramer法則求解線性方程組雖然原則上可行,但因其計算量過大幾乎失去使用價值,但伴隨著計算機的發展,該方法得以應用。解方程組的方法可歸納為直接解法和迭代解法,在數值計算歷史上,直接解法和迭代解法交替生輝。
4 Matlab實現
判斷向量組的線性相關性的方法:(1)求該向量組構成的矩陣的秩,當矩陣的秩小于向量個數時,向量組線性相關;否則,向量組線性無關;(2)求該向量組構成的矩陣的行最簡形,當矩陣的非零行數小于向量個數時,向量組線性相關;否則,向量組線性無關;(3)求以該向量組構成的矩陣為系數的齊次線性方程組的解,當方程組有非零解時,向量組線性相關;否則,向量組線性無關。當線性方程組中方程個數少于變量個數時,方程組有無窮多個解,這時候用Matlab求解得到的是方程組的一個特定解;如果方程的個數多于未知量的個數時,方程組為超定方程組,求得的是一個最小二乘近似解;對于奇異方程組,Matlab不能直接求解,需要對方程組進行同解異構來求解。
注釋
① 劉衛鋒,周長芹.線性代數教學中的矩陣應用實例[J].中國科技信息,2009.11.
② 同濟大學數學系編.線性代數(第五版)[M].北京:高等教育出版社,2006.
③ 王利東,劉婧.從應用實例出發的線性代數教學模式探討[J].數學教育學報,2012.21(3).
④ 高智中,武潔,王洋軍.Matlab在線性代數教學中的幾點認識[J].衡水學院學報,2010.12(1).
⑤ 岳曉鵬,孟曉然.在線性代數教學改革中融入數學建模思想的研究[J].高師理科學刊,2011.31(4).

