灰色系統理論在瀾滄縣松脂產量預測中的應用
呂書文,楊 婧,李 榮
(1.云南省瀾滄縣林業局,云南 瀾滄665600;2.云南農業大學 熱帶作物學院,云南 普洱665000;3.云南省普洱市林業局,云南 普洱665000)
1 引言
自1982年鄧聚龍教授創建灰色系統理論以來,經過30多年的發展完善,形成了較為成熟的理念體系,并在生態建設、區域發展、投資金融、環境治理等眾多領域得到廣泛應用,解決了諸多實際問題,很多基于灰色系統理論的相關預測為政府部門和企業決策提供了科學依據,發揮出較大的社會經濟效益。松脂產業是瀾滄縣林產業的重要組成部分,有效預測松脂產量有助于科學合理調控松脂產業發展。鑒于灰色系統理論在相關預測上表現出的科學性和準確性,筆者嘗試用該理論預測瀾滄縣松脂產量,以便為瀾滄縣林產業發展提供參考。
2 灰色系統理論
灰色系統理論的研究對象是一種不確定性系統,該系統的信息部分能知而部分不可知,通常表現為 “貧信息”和“小樣本”。在評估、診斷、分析、建模、預測、決策、控制和優化不確定性系統方面,灰色系統理論有較好的思路和方法。在應用灰色系統理論對不確定性系統進行預測時,需要對一組原始數據觀測值通過累加等方式進行處理,把它們轉化為新的一組帶有一定規律性的數據序列,再生成擬合微分方程,如果預測精度在允許范圍內,便可利用該方程進行預測。在灰色系統理論的各種預測模型中,最常用的是灰色系統GM(1,1)模型。該模型只要有5個原始數據預測值就可以建模,對一些無規則或不服從任何分布的原始數據也可以通過生成處理轉化為有序序列來建模。該模型具有較高的預測精度,能比較好地反映不確定性系統的實際情況。
2.1 對原始序列進行處理
設有一組原始數據序列為X(0):

對 X(0)作一次累加生成處理得 X(1)為:

其中
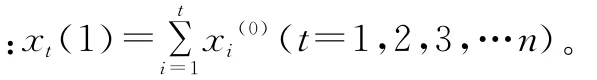
2.2 建立 GM(1,1)模型
對已作累加生成處理后得到的序列X(1)建立灰色系統預測模型的GM方程為:

估計參數a和u,再利用最小二乘法求得:
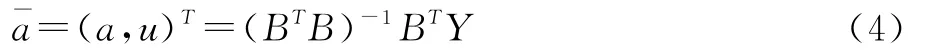
其中:
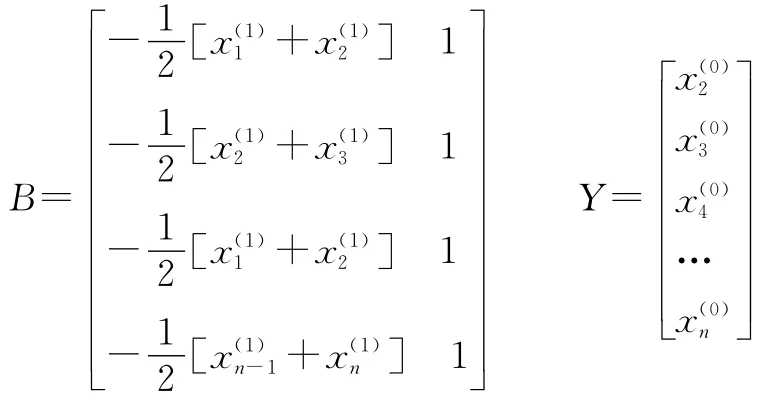
得到灰色系統GM(1,1)預測模型為:
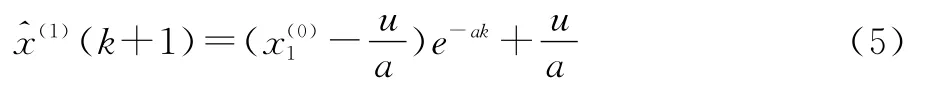
由前可知,序列 X(1)是 X(0)一階累加序列,故原始數據序列的預測值為:

2.3 后驗差檢驗
灰色系統GM(1,1)模型可采用后驗差檢驗的方法確定精度等級。
一般來說,如果小誤差概率P和方差比C都在允許范圍內(表1),那么可以認為灰色系統GM(1,1)模型能夠用來預測不確定性系統的未來情況。
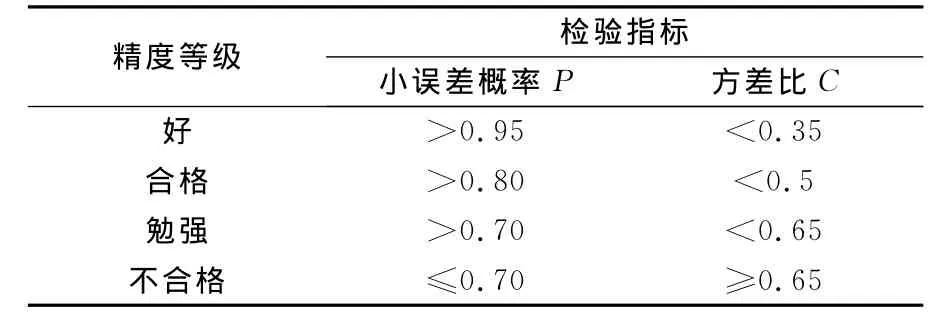
表1 灰色系統GM(1,1)模型精度等級
3 瀾滄縣松脂產量預測
以瀾滄縣2010~2014年松脂產量為原始數據序列,利用灰色系統GM(1,1)模型進行2015年松脂產量預測。
設有瀾滄縣松脂產量原始數據序列為:
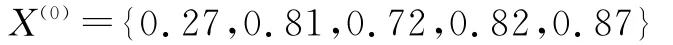
對X(0)作一次累加生成得:
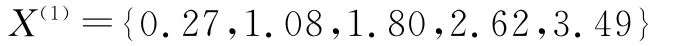
由此可得:
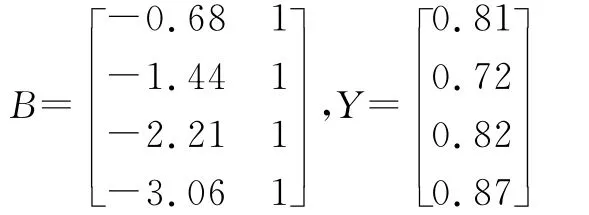
利用最小二乘法可求得:
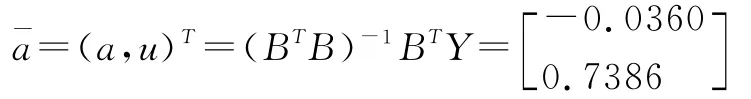
即,a=-0.0360,u=0.7386
故可得到灰色系統GM(1,1)預測模型為:
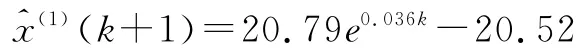
通過計算可知,原始數據標準差:S1=0.8180
絕對誤差系列標準差:S2=0.0592
方差比:C=0.0723
小誤差概率:P=1。
對照表1灰色系統理論GM(1,1)模型精度等級表,可知該GM(1,1)模型預測精度好,可以用于瀾滄縣松脂產量預測(表2)。
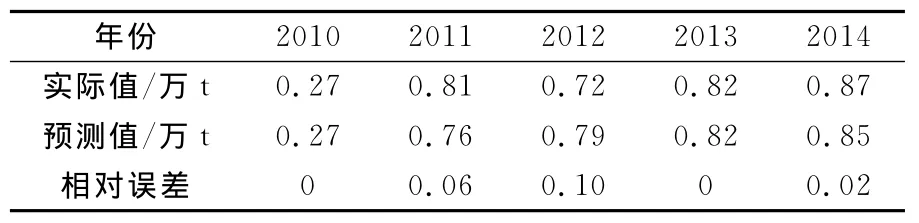
表2 瀾滄縣2010~2014年松脂產量預測值
用灰色系統GM(1,1)模型預測2015年瀾滄縣松脂產量:
令k=5,則有:
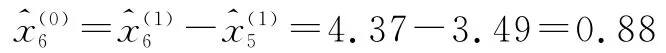
因此,2015年瀾滄縣松脂產量預測值為0.88萬t。
4 結論
用灰色系統GM(1,1)模型在預測瀾滄縣松脂產量的過程中,通過計算得知2015年瀾滄縣松脂產量預測值為0.88萬t。考查瀾滄縣歷年松脂產量的測算數據,2010~2014年測算結果較好,但2012年測算數據與原始數據的相對誤差達到10%,說明原始數據在2012年有所突變,該年份數據在一定程度上沖擊擾動了系統。同時,也說明灰色系統GM(1,1)模型有一定的局限性,在預測松脂產量時,可加入一些定性分析,以彌補原始數據不足導致預測值出現一定的偏差。
[1]李 榮,楊 婧.灰色系統理論在非木材林產品產量預測中的應用[C]//李 榮,楊 婧.守望綠色——基層林業論文集.昆明:云南美術出版社,2011:238~241.
[2]李 榮,楊 婧.灰色系統理論在松毛蟲發生面積預測中的應用[J].西部林業科學,2014(增刊):40~42.

