無速度測量下基于信息耦合度的自主水下航行器分群控制算法

楊盼盼，劉明雍，雷小康，武小金

（西北工業大學航海學院，陜西西安710072）

無速度測量下基于信息耦合度的自主水下航行器分群控制算法

楊盼盼，劉明雍，雷小康，武小金

（西北工業大學航海學院，陜西西安710072）

自主水下航行器（AUV）的分群控制，表征為AUV群集在外部刺激下自發分裂成多個子群的行為。針對無速度測量下AUV群集（SAUV）的分群控制問題，提出了一種基于信息耦合度的分群控制算法。該算法利用信息耦合度表征AUV間的交互作用強度，并通過對個體運動的動態調節實現群集行為的分化。在此基礎上，針對AUV分群過程中無速度測量的情況，通過設計分布式觀測器對鄰居速度信息進行實時估計，并將最大信息耦合度鄰居的位置信息融入分群控制律中，實現了外部刺激下AUV群集的自發分群運動。理論分析和仿真實驗均驗證了所提分群控制算法的可行性和有效性。

控制科學與技術；自主水下航行器；分群控制；信息耦合度；速度觀測器

0 引言

自主水下航行器群集（SAUV）的協同控制是目前海洋工程領域的熱點研究問題之一，在大范圍海洋聯合自主采樣、海底大規模勘探、水下多目標協同搜索等許多方面有著廣闊的應用前景［1］。通常，自主水下航行器（AUV）群集的協同行為分組群和分群［2］兩種。組群要求在一定區域內隨機分布的AUV能聚集在一起，并以編隊的形式協調的執行共同任務；與組群相反，分群表征為AUV群集在外部刺激下自發分裂成若干個子群的行為，可用于分群避險［3］、分群監控［4］、分群追蹤［5-6］、分群搜索等場合，對提高整個群集的任務執行效率和生存概率有十分重要的意義。

目前，對AUV群集協同行為的研究多集中在以編隊協同為代表的組群控制中，而關于分群控制的研究，尚處于十分欠缺的階段。已有成果多利用個體間的顯式差異或身份標識［7］，采用協商［4］、指派［5-6］等智能機制，在多目標跟蹤及動態任務分配中實現群集的分裂行為。如Kumar等［7］采用不同的人工勢場實現了異構系統中群集機器人的分離；La等［4］以協商方式，通過分群實現移動傳感器網絡對多個目標的動態跟蹤與監視；劉宗春等［5］通過為不同的個體設定相應的跟蹤目標，使群集在宏觀層面上展現出分裂現象；Su等［6］通過對多個虛擬領航者的跟蹤，實現了一個母群分裂成多個子群的行為。

對于AUV群集而言，個體配置簡單、能力有限、地位均等無主從之分，其行為僅受周圍鄰居的影響，相互間不存在任何形式的協商、指派等高級智能化的協調機制。因此，AUV群集的分群運動實質上是一種無中心控制的涌現行為。針對此類群集系統的分群控制問題，劉明雍等［8］、雷小康等［9］模擬自然界中鳥群/魚群的分群行為，提出了基于鄰域跟隨的分群控制方法，實現了群集系統的自組織分群運動。

然而，劉明雍等［8］、雷小康等［9］所提分群控制方法，要求個體同時獲知鄰居的位置和速度信息，但對于AUV群集而言，囿于成本所限，不可能為每個AUV都裝配高精度的速度測量傳感器，加之水下測量普遍存在的時延、噪聲干擾等因素，使得AUV速度信息的實時獲取更加困難。因此，為了降低系統的硬件復雜度，節約設備成本，減少個體間交互信息量，本文研究了無速度量測下，不依賴于指派、協商等智能化機制，僅通過AUV間的局部交互而自發涌現出分裂現象的分群控制問題。首先提出了一種基于信息耦合度（ICD）的分群控制策略。在此基礎上，針對AUV間無速度信息量測的情況，僅利用位置信息通過設計分布式觀測器對速度進行實時估計，實現無速度測量下AUV群集在外部刺激下的自發分群運動。仿真實驗驗證了該算法的有效性。

1 問題描述

考慮由N個AUV組成的群集系統，忽略其復雜的動力學特性，個體運動方程可由如下簡化模型進行描述：

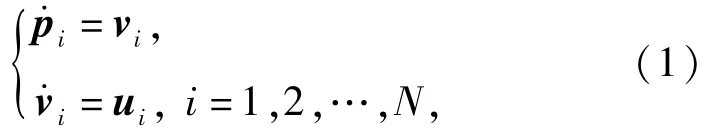
群集中AUV間的交互作用關系可用無向圖G=（V，E，A）來進行描述［10］，其中：V=｛n1，n2，…，nN｝表示頂點集，由N個AUV組成；E=｛（ni，nj）∈V×V｝為邊集，由AUV間的鄰接關系確定；用A=［aij］表示頂點與邊之間的關系，若（ni，nj）∈E，則aij=1，否則，aij=0.圖G的Laplacian矩陣可表示為L=D-A，其中，D=［diag（di）］為入度矩陣，為頂點i的入度。集合表示AUV i的鄰居集，其中R為AUV的感知半徑，‖pi-pj‖為AUV i與AUV j間的歐氏距離。

本文研究無速度測量下AUV群集的應激分群問題，其目的在于不借助于任何協商、指派或集中式控制等智能化方式，僅通過個體間的局部信息交互，在無速度量測的情況下，利用周圍鄰居的位置信息，使AUV群集在外部刺激下涌現出自發分裂成若干個子群的運動行為。

2 無速度測量的AUV分群控制算法

2.1 基于信息耦合度的分群策略

分群行為的實質是多元外部刺激信息在群集中傳播引起的一種個體運動分化現象［3］。研究表明：在外部刺激下，個體間關聯強度不同導致的運動趨向性差異可使群集產生分裂行為［11］。因此，個體間的關聯程度在AUV群集的分群過程中發揮關鍵作用。本文采用信息耦合度表征AUV間的關聯強度，并根據個體間的關聯程度對周圍鄰居位置及相對運動敏感的特性［9，12］，將其具體形式設計為

式中：ξij為位置耦合項，與AUV間的相對位置有關，可寫為

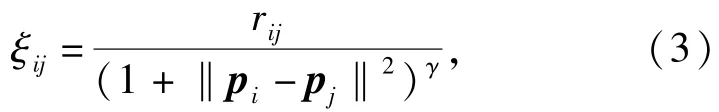
式中：rij為位置耦合強度系數，且rij＞0；γ為固定參數，且γ＞0；ωij為相對運動耦合項，由單位時間內AUV間相對位置的變化進行描述［9］：

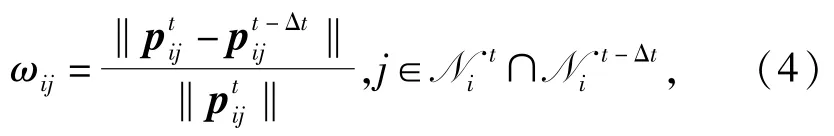
分群過程中，AUV通過與其鄰居集中信息耦合度最大個體建立強耦合作用，可實現外部刺激信息在群集中的定向傳播，從而為分群運動的實施奠定基礎［13］。基于這種思想，與AUVi存在最大耦合強度的個體fi從其鄰居集Ni中選擇產生，選取規則為

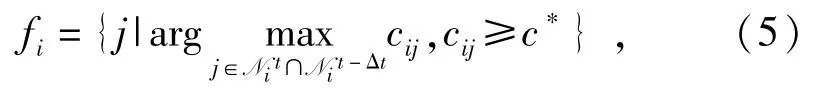
式中：c*＞0為分群行為是否發生的判斷閾值。選取較大的c*有助于克服個體的隨機波動對群集行為的影響，以防止群集在擾動下進入無組織分裂的混亂狀態，可增強系統的魯棒性。

需要注意的是，當AUV間的信息耦合度小于分群閾值時，群集保持原運動狀態，不發生群集分裂行為。

2.2 無速度測量的AUV分群控制律

對于無速度測量的AUV群集系統而言，由于僅依賴位置測量，個體間交互信息減少，運動不確定性增大，已有的基于位置和速度信息的分群控制方法［8-9］并不能保證分群行為的順利實施。在此，利用AUV的位置信息構建分布式觀測器，從而實現對速度信息的估計，并將最大信息耦合度鄰居位置信息融入分群控制律中，可得分群控制算法：

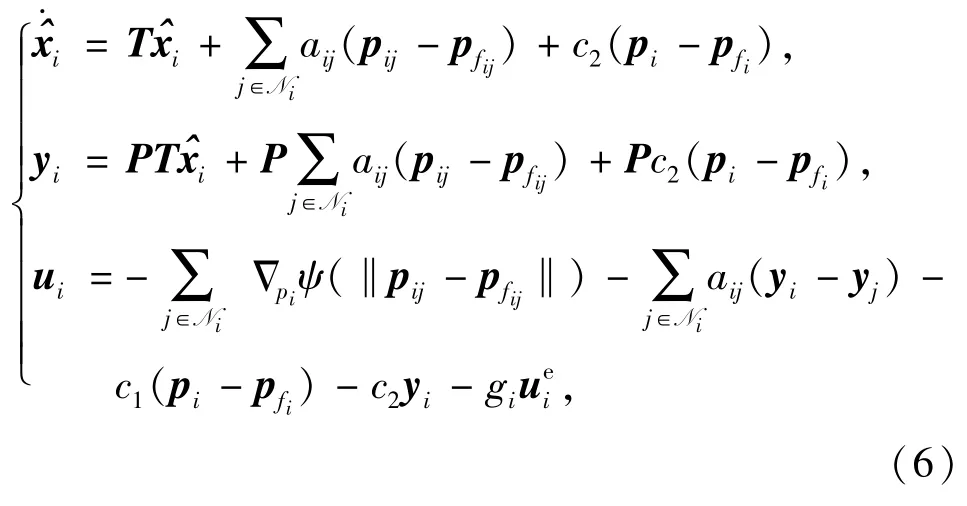
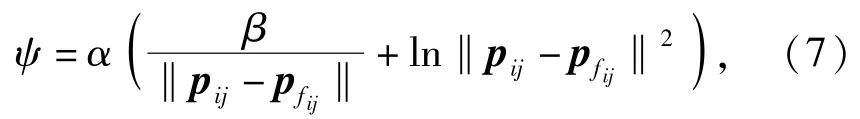
式中：α為勢場強度系數；β為群集結構系數。

AUV群集分群運動的實質是外部刺激下個體行為分化現象，群集是否具有分群能力，完全取決于個體間所遵循的協同規則［2，8］。因此，在不引起歧義的前提下，本文在后續分析過程中忽略外部刺激，重點關注分群過程中個體間的內部交互機制，僅在最后仿真實驗中引入多元外部刺激信號作為分群行為的觸發項。

分群過程中，個體最大信息耦合度鄰居fi在每個采樣時刻按照（5）式動態更新，因此每個AUV并不存在一個固定的領航者或跟蹤目標，而是通過信息耦合度在采樣間隔與周圍特定鄰居建立強交互作用實現外部刺激信息的定向流轉，從而以分布的方式實現群集的自組織分群行為，這與文獻［5-6］采用指派方式基于多目標跟蹤的分群控制方法有本質區別。

當多元外部刺激作用在AUV群集中部分個體上，并使這些個體的運動行為產生分化時，在無速度量測的情況下，利用（6）式可實現AUV群集的自組織分群行為，每個子群以編隊的方式獨立運行，且個體運動狀態最終與該子群中運動行為突變AUV的速度漸近趨于一致。

2.3 理論分析

選取AUV i鄰域范圍內的Ni個鄰居進行研究，并假設在時間段t～t+Δt內，圖GNi保持連通。選擇如下半正定Lyapunov能量函數：

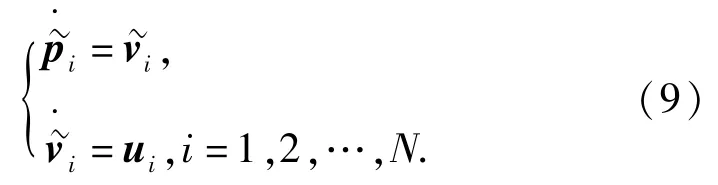
同理，（6）式可表示為

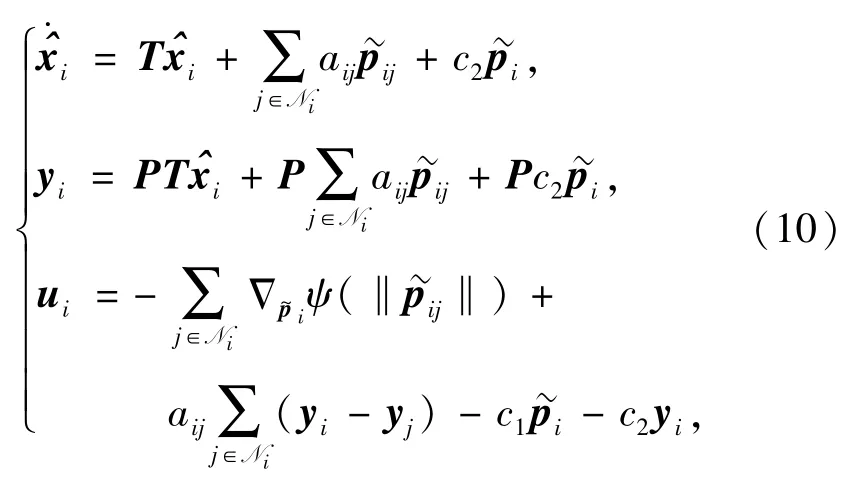
此時，選取的能量函數（8）式可寫為

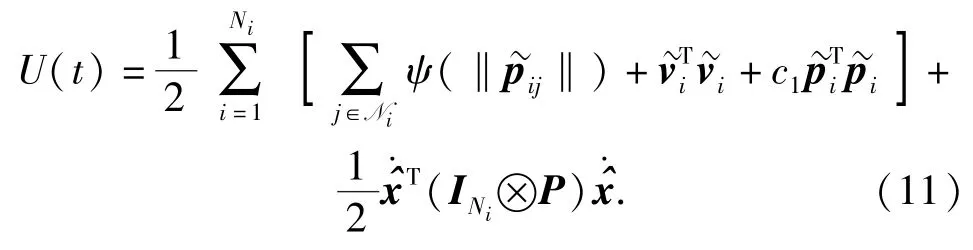
根據人工勢場函數ψ和鄰接矩陣A的對稱性，可得

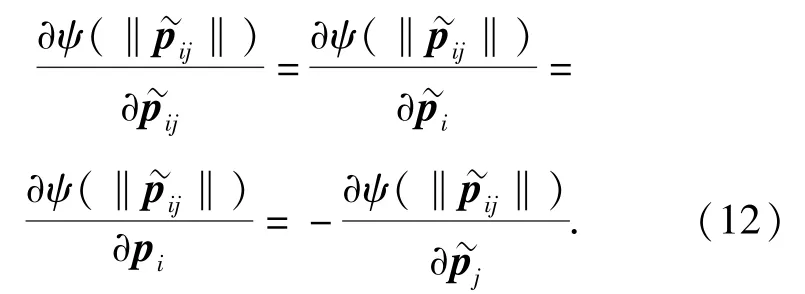
對U（t）求時間導數，可得

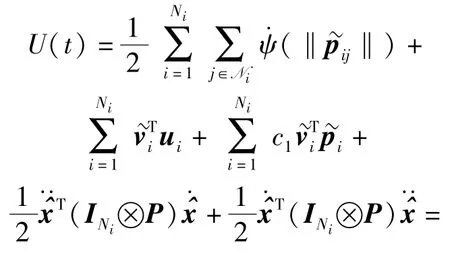
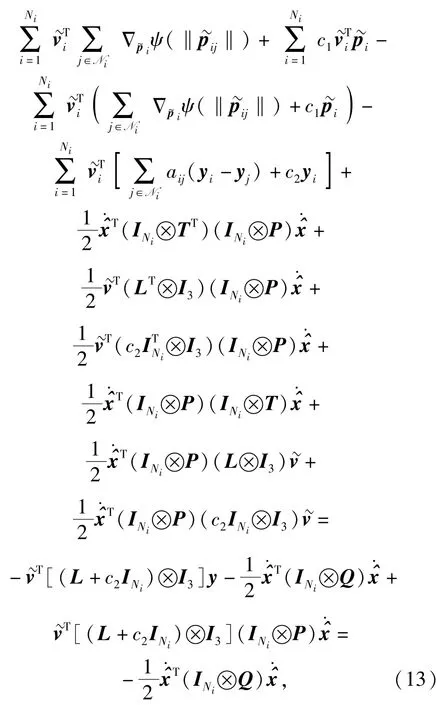
式中：INi和I3分別為Ni維和三維單位矩陣；L為圖GNi的Laplace矩陣；；.

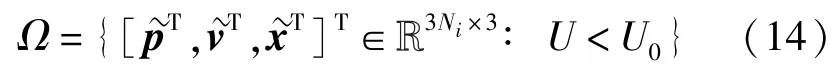
是不變緊集。根據LaSalle不變集定理，從Ω出發的所有AUV的軌跡趨近于以下最大不變集內：

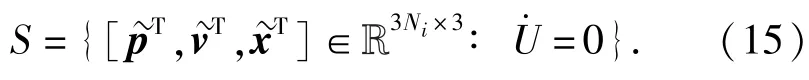
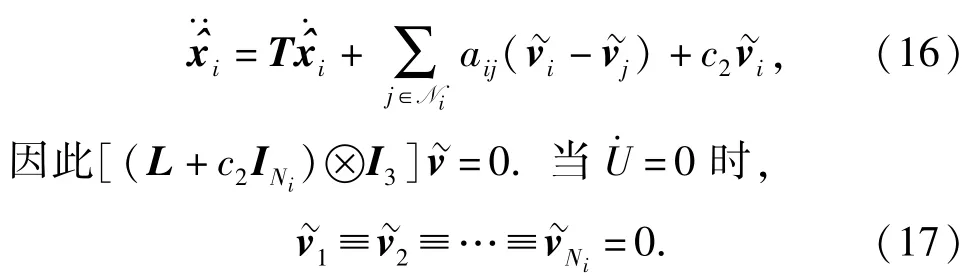
上述條件當且僅當vi=vfi時成立，即每個AUV的速度與其最大信息耦合度鄰居fi的速度趨于一致。

不失一般性，假設AUV l為子群中感受外部刺激并做出機動運行的個體，由于在有限時間段t～t+Δt內，圖GNi保持連通，圖中的所有個體都與AUV l間存在連通路徑，即在鄰居集中存在以AUV l為根節點的生成樹。因此，在（6）式作用下，鄰居集中所有AUV個體的速度最終會與AUV l的速度漸近趨于一致。

綜上可知，對于AUV群集系統而言，其在外部刺激下導致少數AUV運動行為突變且發生分化時，在本文所設計的分群控制方法下，僅利用位置信息，AUV速度將與其鄰域內運動突變個體趨于一致，從而使群集中的子群向著不同的方向運動，最終實現AUV群集的自組織分群運動行為。

3 仿真研究

3.1 仿真實驗設置

為簡化起見，選取在定深空間沿二維平面運行的20個AUV作為仿真實驗對象。假設其初始位置隨機分布在20 m×20 m的平面內，初始速度隨機分布在［0，10］m/s×［0，10］m/s內，仿真步長取0.005 s.其他仿真參數為：R=5 m，c*=0.3，rij=1， γ=1，α=15，β=3，c1=12，c2=20，Δt=0.005 s，

假設AUV群集首先從初始位置聚集并做編隊運行，其運行速度為［5，5］Tm/s.t=5 s時，群集邊緣的兩個AUV，記為AUV 1和AUV 2，分別感受到不同方向的兩個外部刺激信號：

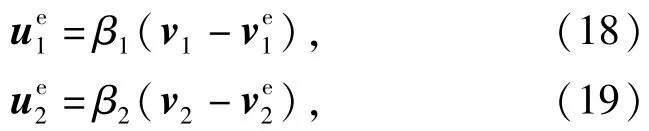
式中：v1=［10，0］Tm/s和v2=［0，10］Tm/s分別為外部刺激期望的運動速度；選取較大的反饋增益系數β1=β2=100可使得刺激信號遠大于群集內部作用力，從而使AUV 1和AUV 2朝不同的方向運動。

為更直觀地分析分群過程中AUV的位置分布情況，引入群集平均距離davg對分群過程中AUV的相對位置情況進行描述：

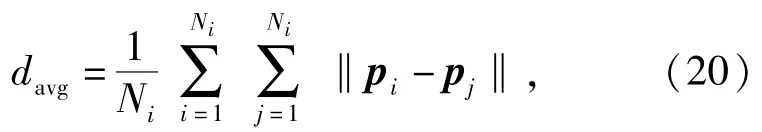
式中：Ni為群集中AUV數量。當davg保持恒定時，群集中AUV的位置處于相對穩定狀態；反之，群集中AUV間存在相對運動，群集狀態不穩定。

3.2 仿真結果及分析

3.2.1 基于速度估計的仿真結果

對基于速度估計的分群控制算法進行的仿真驗證結果如圖1～圖3所示。

圖1 AUV分群過程中運動曲線Fig.1 Trajectories of AUVs

圖1為AUV分群運動的演化過程，其中圓圈代表AUV個體，曲線為AUV的運動軌跡。圖1（a）為t=0 s時刻AUV的位置分布狀況；圖1（b）為AUV群集在未受到外部刺激時（t＜5 s）運動狀態，群集從初始隨機分布狀態聚集并做編隊運行；圖1（c）為t=6 s時，群集受到外部刺激后，部分AUV在外部刺激作用下運動行為出現沖突，導致群集整體行為產生波動并呈分裂趨勢；圖1（d）為t=12 s時，群集的最終運動狀態，AUV群集從一個緊致的母群分裂成兩個獨立運行的子群。

圖2 分群過程中AUV速度曲線Fig.2 Velocity curves of AUVs

圖2為分群過程中AUV在x方向和y方向上速度分量的變化曲線。由圖2可見，在編隊運行過程中（t＜5 s），各AUV的運動速度逐漸趨于一致；當外部刺激下分群行為開始后（t＞5 s），分離出的兩個子群運動速度產生分化，最終子群1和子群2在x方向和y方向上速度各自趨于其一致值，即［vx1，vy1］T=［10，0］Tm/s，［vx2，vy2］T=［0，10］Tm/s.

圖3為分群過程中AUV群集平均距離曲線。其中，davg1和davg2分別表示子群1和子群2中AUV間的平均距離。由圖3可見，在AUV群集做編隊運行時（t＜5 s），群集中個體間平均距離保持在大約3 m左右的穩定狀態；在t=5 s時，外部刺激出現后，在分群控制律的作用下，群集運動行為產生分化，子群1和子群2的個體平均距離davg1和davg2最終保持在3 m左右的穩定狀態，而AUV整體平均距離davg隨著分群過程的持續，逐漸增大呈發散趨勢，表明子群1和子群2的間距不斷增大，AUV群集最涌現出分群行為。

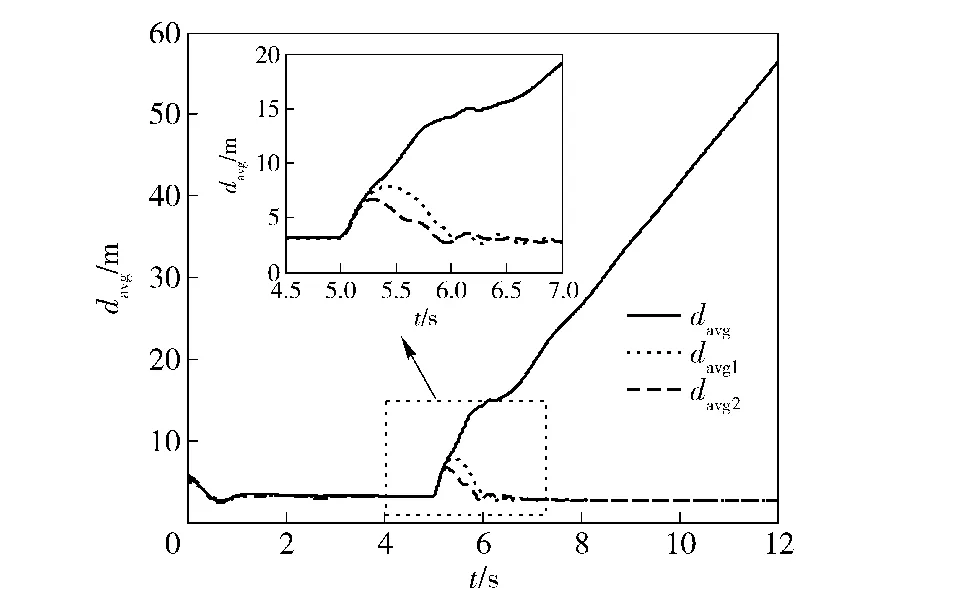
圖3 分群過程中AUV平均距離曲線Fig.3 Average distances between AUVs

3.2.2 無速度估計的仿真結果

若不利用速度觀測器對速度進行估計，僅基于位置信息的分群控制律可寫為

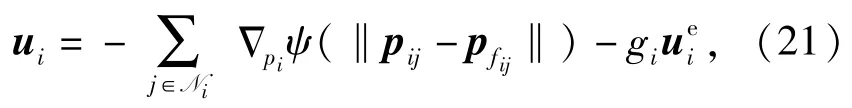
即AUV間僅通過人工勢場進行位置協調。在3.1節的實驗設置下，其仿真結果如圖4和圖5所示。

由圖4和圖5可見，在無速度估計的情況下，AUV群集的運動不確定性增大，當外部刺激出現時（t=5 s），速度不能分別收斂到一致狀態，導致AUV群集陷入混亂狀態，不能實現期望的分群行為。

仿真結果及對比表明：本文所設計的無速度測量下、基于信息耦合度的分群控制算法，不依賴于指派、協商等機制，即能實現無中心控制的AUV分群運動行為，分裂出的子群速度逐漸趨于一致，能以編隊的方式獨立運行。而僅利用位置信息，不進行速度估計時AUV速度不能實現有效收斂，由于量測信息的缺乏，分群過程中不確定性增大，甚至不能實現分群。

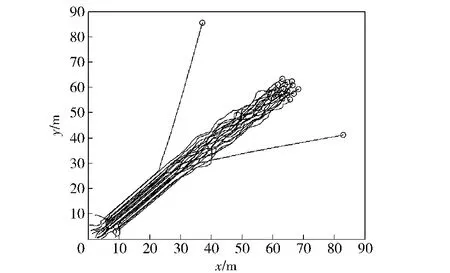
圖4 無速度估計時AUV群集軌跡曲線Fig.4 Trajectories of AUVs without velocity estimation

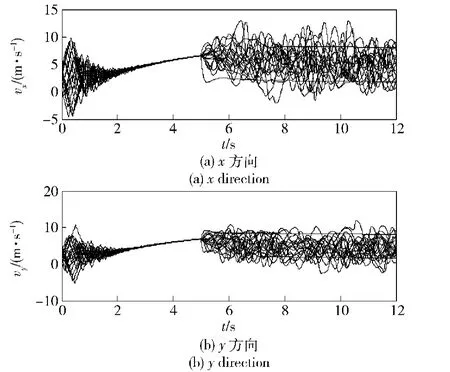
圖5 無速度估計時AUV速度曲線Fig.5 Velocity curves of AUVs without velocity estimation

4 結論

本文針對無速度測量下AUV群集的分群控制問題，提出了一種基于信息耦合度的分群控制算法。該方法降低了對AUV系統的配置要求，放寬了分群過程中對速度信息的依賴，簡化了AUV系統配置，減少了水下測量的信息量，增強了分群控制算法的實用性，適用于大批量AUV分群協作的應用場合。

（

）

［1］許真珍，封錫盛.多UUV協作系統的研究現狀與發展［J］.機器人，2007，29（2）：186-192.XU Zhen-zhen，FENG Xi-sheng.Current status and future directions of multiple UUV cooperation system［J］.Robot，2007，29（2）：186-192.（in Chinese）

［2］Couzin I D，Laidre M E.Fission-fusion populations［J］.Current Biology，2009，19（15）：633-635.

［3］Bajec I L，Heppner F H.Organized flight in birds［J］.Animal Behaviour，2009，78（4）：777-789.

［4］La H M，Sheng W.Dynamic target tracking and observing in a mobile sensor network［J］.Robotics and Autonomous Systems，2012，60（7）：996-1009.

［5］劉宗春，田彥濤，李成鳳.動態阻尼環境下多領導者群體機器人系統協同跟蹤控制［J］.機器人，2011，33（4）：385-393. LIU Zong-chun，TIAN Yan-tao，LI Cheng-feng.Co-adaptive following control of swarm robot system with multiple leaders in dynamic damping environment［J］.Robot，2011，33（4）：385-393.（in Chinese）

［6］Su H S，Wang X F，Yang W.Flocking in multi-agent systems with multiple virtual leaders［J］.Asian Journal of Control，2008，10（2）：238-245.

［7］Kumar M，Grag D P，Kumar V.Segregation of heterogeneous units in a swarm of robotic agents［J］.IEEE Transactions on Automatic Control，2010，55（3）：743-748.

［8］劉明雍，雷小康，彭星光.融合鄰域自適應跟隨的群集系統分群控制方法研究［J］.西北工業大學學報，2013，31（2）：250-254. LIU Ming-yong，LEI Xiao-kang，PENG Xing-guang.A control algorithm for flock fission based on adaptive local following interaction［J］.Journal of Northwestern Polytechnical University，2013，31（2）：250-254.（in Chinese）

［9］雷小康，劉明雍，楊盼盼.基于鄰域跟隨的群集系統分群控制算法［J］.控制與決策，2013，28（5）：741-745. LEI Xiao-kang，LIU Ming-yong，YANG Pan-pan.Fission control algorithm for swarm based on local following interaction［J］.Control and Decision，2013，28（5）：741-745.（in Chinese）

［10］Godsil C，Royle G.Algebraic graph theory［M］.Berlin：Springer-Verlag，2001.

［11］Couzin I D，Krause J，Franks N R，et al.Effective leadership and decision making in animal groups on the move［J］.Nature，2005，433（7025）：513-516.

［12］Li J C，Sayed A H.Modeling bee swarming behavior through diffusion adaptation with asymmetric information sharing［J］.EURASIP Journal on Advances in Signal Processing，2012（1）：1-17.

［13］Nagy M，ákos Z，Biro D，et al.Hierarchical group dynamics in pigeon flocks［J］.Nature，2010，464（7290）：890-893.

Information Coupling Degree-based Fission Control Algorithm for Autonomous Underwater Vehicles without Velocity Measurements

YANG PAN-pan，LIU Ming-yong，LEI Xiao-kang，WU Xiao-jin
（School of Marine Science and Technology，Northwestern Polytechnical University，Xi'an 710072，Shaanxi，China）

The fission control of autonomous underwater vehicles（AUV）presents a behavior of that a cohesive AUV swarm is split into multiple sub-swarms under external stimulus.An information coupling degree-based fission control algorithm is proposed for the fission control of swarm AUVs（SAUVs）without velocity measurements.Information coupling degree is utilized to denote the interaction intensity between AUVs，which realizes the behavior divergence of AUVs by adjusting their motion states.For the absence of velocity measurements，a distributed velocity observer is designed to estimate the velocities of AUVs in real time.By integrating the position information of the most correlated neighbor into the fission control law，the spontaneous fission behavior of AUVs can be achieved without velocity measurements.Both theoretical analysis and experimental simulation demonstrate the feasibility and effectiveness of the proposed fission control algorithm.

control science and technology；autonomous underwater vehicle；fission control；information coupling degree；velocity observer

TP242.3；TP273

A

1000-1093（2015）05-0891-07

10.3969/j.issn.1000-1093.2015.05.019

2014-05-23

國家自然科學基金項目（51179156、51379176）

楊盼盼（1985—），男，博士研究生。E-mail：yangpanpan1985@126.com；劉明雍（1971—），男，教授，博士生導師。E-mail：liumingyong@nwpu.edu.cn