攻防對抗中指數射擊策略最優性分析

李龍躍，劉付顯，趙麟鋒，王東旭

（空軍工程大學防空反導學院，陜西西安710051）

攻防對抗中指數射擊策略最優性分析

李龍躍，劉付顯，趙麟鋒，王東旭

（空軍工程大學防空反導學院，陜西西安710051）

研究了紅藍攻防對抗中的射擊策略優化問題，即研究紅方面對多個藍方目標，如何射擊能獲得最大收益的問題。基于以往研究的局限性，為平衡紅方射擊收益和自身存活概率，引入和拓展Gittins指數應用于射擊決策問題，考慮了藍方目標退出戰斗的可能性，以紅方在自身被摧毀之前最大化殺傷藍方目標的收益（或數量）為目標，對指數射擊策略的最優性進行了討論，拓展了定理1、定理2，給出推論1.為進行比較，引入近視策略、完全策略和循環策略3種截然不同的射擊策略，并給出近視策略最優性定理3.實例設置了兩個射擊場景，在4種射擊策略下計算紅方的收益情況、殺傷目標情況和自身被摧毀情況，驗證了指數射擊策略的最優性。

兵器科學與技術；射擊決策；Gittins指數；指數策略；近視策略

0 引言

很多軍事作戰問題可以抽象為我方（防御方，稱為紅方）防御多個敵方（進攻方，稱為藍方）的射擊戰斗問題。典型如地空導彈射擊多個空氣動力目標或反輻射導彈的防空作戰場景，藍方目標可能有多個類型，紅方不能完全確定藍方目標的類型，而且紅方也可能被藍方摧毀而喪失戰斗能力；再如高炮對空射擊、陸軍坦克交戰和水面艦艇編隊防空等都是攻防對抗過程［1-2］。Gittins首先提出了最優Gittins指數用于解決特定類型的多臂bandit問題，賦予每一個bandit收益指數，并建立bandit狀態函數，基于指數最大化來研究決策問題［3］。近年來，Anderson［4］、Gu等［5］、Sonin［6］、Kumar［7］、Si等［8］對Gittins指數理論研究及在資源調度、任務分配和隨機決策等領域的應用進行了極大的拓展。Glazebrook等結合Gittins指數討論了多臂bandit框架下的軍事射擊優化問題［9］，而后Barkdoll等和Glazebrook等一起對該問題進行了一系列深入研究［10-11］。紅藍雙方攻防射擊對抗過程本質上是分配紅方可用射擊資源，去射擊固定集合的藍方來襲目標的過程，紅方射擊策略的優劣對射擊收益、殺傷藍方目標數量和紅方生存概率都有影響，因此，紅方制定和選用最優射擊策略對于獲取最大射擊收益至關重要。

1 問題分析

Barkdoll等［12］描述的非對稱攻防對抗射擊場景中（如地面防空襲作戰），藍方具有一定優勢，如果紅方不能成功射擊藍方目標，則自己將會置于可能被藍方（反輻射導彈）摧毀的境地，因此紅方需對每一個藍方目標賦予一個“值”。這個值一般用來體現藍方目標突防后對紅方造成的損失，也可稱為威脅值。紅方射擊作戰目標為在自己未被摧毀的情況下，最大化殺傷藍方目標的期望收益或最小化藍方目標突防造成的損失。但Barkdoll等［12］對這種情況考慮還不完全，其研究存在局限性：1）紅方賦予藍方目標的威脅“值”并非恒定不變的。如隨著戰斗進行，紅方獲得更充分的目標指示后或得知目標受損等情況都會導致目標威脅值的變化，因此威脅值應該是動態變化的；2）紅方被摧毀的概率與其選擇射擊的藍方目標息息相關，如地空導彈射擊距離較遠的目標時，需輻射更遠、更強的雷達波去導引攔截彈射擊目標，增加了被反輻射彈道發現和鎖定的概率，從而將自己置于較危險的境地。因此紅方需考慮射擊特定藍方目標時給自己帶來的風險；3）紅方所需射擊的藍方目標會隨著時間發生變化，新的目標可能會不斷到達，舊的目標可能會退出或突防出紅方射擊范圍。此外，紅方有可能無法得知目標所處狀態，如以往射擊對藍方目標的殺傷效果等信息。基于以上問題，本文通過引入和拓展指數策略應用于攻防對抗中射擊策略選擇問題，以紅方在自身被摧毀之前最大化殺傷藍方目標的收益（或數量）為目標，對指數射擊策略的最優性進行了討論，并給出定理2、推論1和定理3（近視策略），旨在最大化紅方作戰收益，對于輔助紅方射擊決策和建設作戰指揮信息系統具有一定借鑒意義。

2 攻防對抗射擊的馬爾可夫決策過程

考慮一個紅方火力單元射擊N個藍方目標的問題，規定“一次戰斗”至少包括紅方對藍方進行一次射擊（期間紅方有可能被藍方摧毀），也可能包括紅方對藍方目標殺傷效果的觀察過程。假設紅方射擊彈藥數量不受限制，此時紅方的核心決策問題在于如何根據以往的射擊戰斗情況，選擇下一個需要射擊的目標，從而最大化射擊過程中的期望收益。紅方射擊藍方目標的決策問題可描述為馬爾可夫決策過程｛（Ωj，ωj，Pj，Rj，Qj，β），1≤j≤N｝［13］.具體為：

1）X（t）=｛X1（t），X2（t），…，XN（t）｝表示在時刻藍方的狀態（t+1時刻之前）。Xj（t）表示藍方目標j（1≤j≤N）的狀態。

2）Xj（t）∈Ωj∪｛ωj｝.Ωj為紅方對藍方目標j所有可能狀態的認知空間（可數）；Xj（t）=ωj表示在t時刻，紅方射擊藍方目標j時被摧毀。

3）XN+1（t）的值為0表示在時刻t紅方選擇退出戰斗或被摧毀，否則其值為1，假設XN+1（0）=1.

6）標記函數Qj滿足

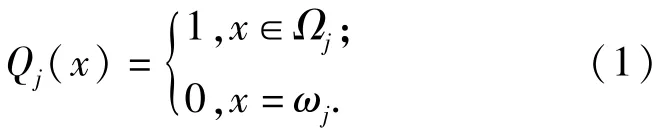
標記Qj（x）表明，如果紅方被摧毀，則收益為0，下一時刻停止射擊或目標飛出射擊時間窗口收益也為0，即

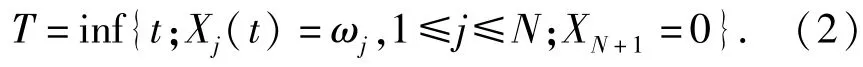
7）如果紅方在t時刻執行射擊行動aj，藍方目標由Xj（t）變為Xj（t+1）的概率由馬爾可夫定律Pj決定：

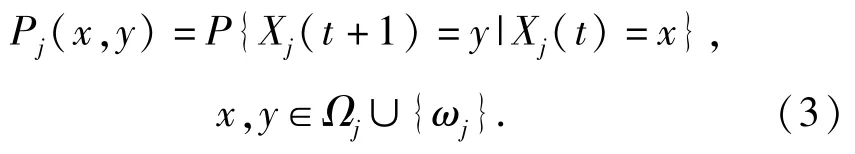
注意到狀態空間Ωj包含紅方得知藍方目標j被殺傷狀態，因此和ωj都是Pj下的吸收狀態。為描述射擊行動的期望收益，引入有界函數Rj，Qj，.令Xj（t）=x，Rj（x）為在t時刻紅方執行行動aj的期望收益。令，則紅方在t時刻執行行動aj的期望收益可寫成

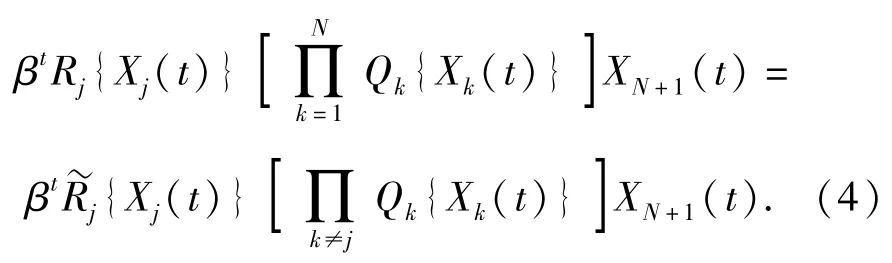
由（4）式的Qk乘積項可知，如果紅方在射擊過程中被摧毀，則收益為0，β的取值一般由決策者自行設定［14］。通過引入折扣因子β∈（0，1）來更加準確描述實際戰斗和增強模型的通用性，此外如果紅方面臨的威脅不僅僅是藍方來襲目標，則β可看成是紅方單位時間內在所有外在威脅下的生存概率，在時刻紅方執行行動aN+1的收益為βtRd，Rd為紅方終止射擊時的收益。

3 指數射擊策略

紅方射擊策略本質是基于歷史射擊效果，決策每一時刻射擊藍方目標行動的一種規則。如射擊策略用v表示，v（t）表示t時刻紅方選擇的行動，則策略v下總的射擊過程期望收益可表示為

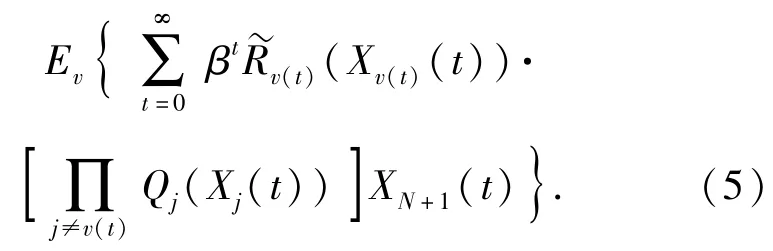
本文研究射擊策略的目的在于找到最優射擊策略v*，使得紅方射擊期望收益最大。廣義bandits決策過程是馬爾可夫決策過程的一種，其在不同決策行為之間引入了相互獨立的決策收益，可作為研究射擊問題的框架。對于廣義bandits決策過程存在最優射擊策略，有定理1.

定理1［15］存在函數，假設在t時刻紅方未被摧毀，

1）紅方的最優策略是射擊藍方目標j*，當藍方目標j*滿足（6）式時成立：

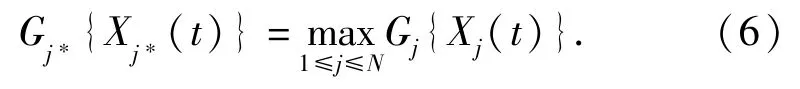
2）紅方的最優策略是終止射擊，滿足（7）式時成立：

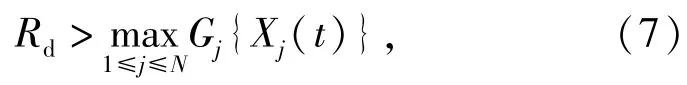
式中：Gj（x），x∈Ωj為Gittins指數。令τ為紅方射擊過程結束時刻，表示在［0，τ）時間段紅方的射擊期望收益，則

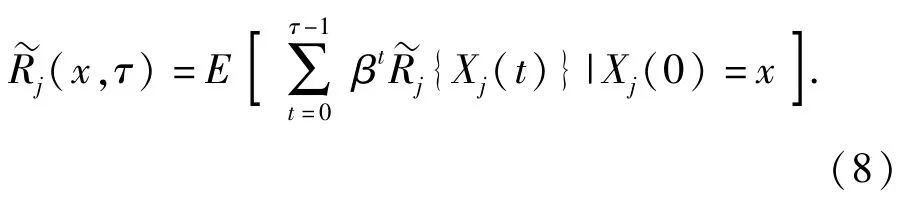
當紅方被摧毀時，則紅方收益也被終止，其收益率［15］為

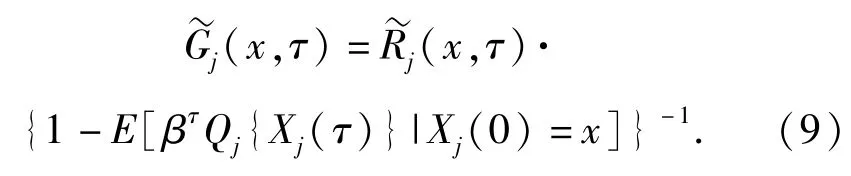
令指數Gj（x）為最大值，即

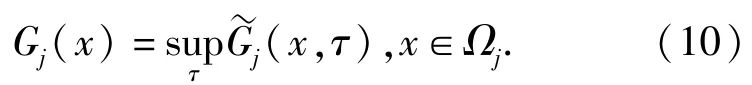
考慮第1節提到的以往研究的局限性，對紅方射擊N個藍方目標問題，假設藍方目標有B種類型（類型是指隨著射擊戰斗進行，可決定射擊結果的藍方目標特征的總稱，需要依據具體問題分析）。通常情況下，紅方不能確定N個藍方目標的類型，這種對目標類型的不確定性由N個獨立先驗分布∏1，∏2，…，∏N表示，其中，表示紅方判定藍方目標j屬于b類型的概率。設在1次戰斗中，藍方目標的類型不會改變，所有射擊結果相互獨立，紅方對藍方b類型目標的殺傷概率為rb，被其摧毀的概率為θb，紅方對藍方b類型目標的殺傷失敗，目標退出戰斗的概率為φb.紅方在第t次射擊殺傷一個藍方b類型目標的收益為βtRb，紅方的戰斗目標是在被摧毀前最大化殺傷藍方目標所獲得的收益。當β=1，Rb=1時，紅方的戰斗目標是在被摧毀前最大化殺傷藍方目標的數量。基于貝葉斯理論，在經歷n次戰斗后，如果紅方和藍方目標j均存活，則此時紅方判定藍方目標j屬于b類型的概率可由后驗分布來表示：

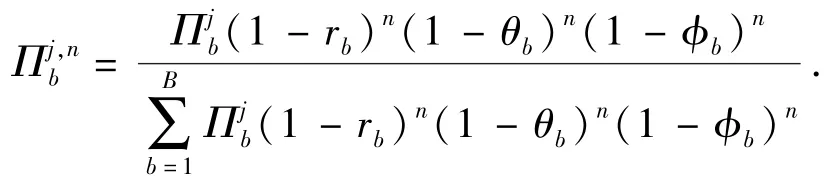
由第2節分析顯然有

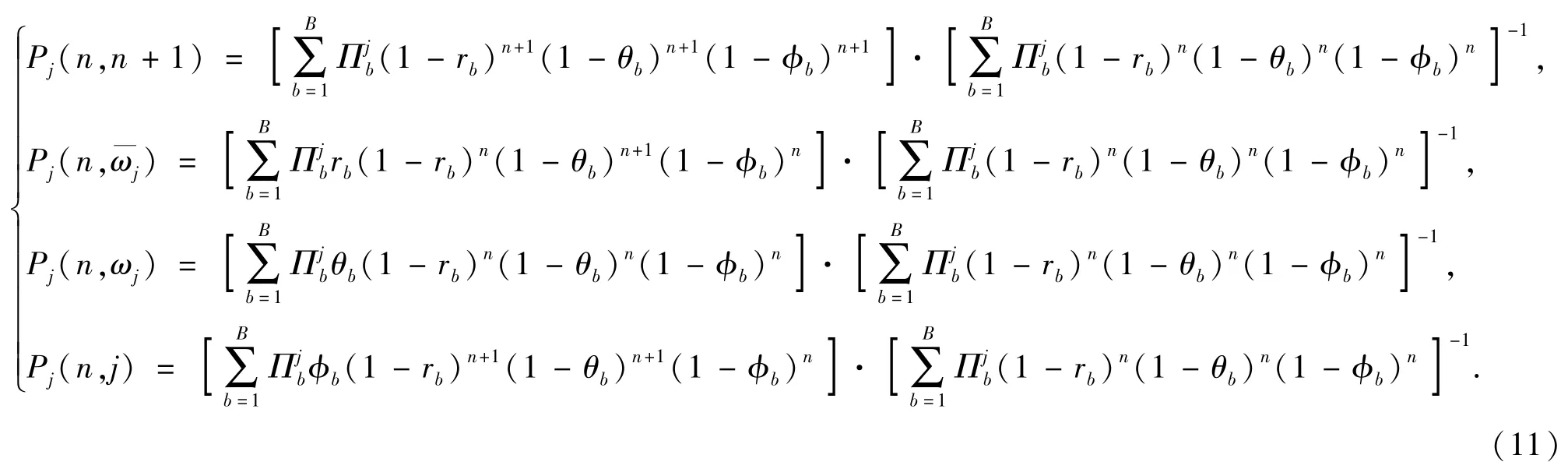
（11）式的4個公式分別表示紅方和藍方目標j均存活、紅方存活藍方目標j被殺傷、紅方被摧毀和紅方和藍方目標j均存活且藍方目標j退出戰斗。4種情況下射擊行動的期望收益（不帶折扣因子）為聯立（9）式、（10）式、（13）式和（14）式可得定理2.

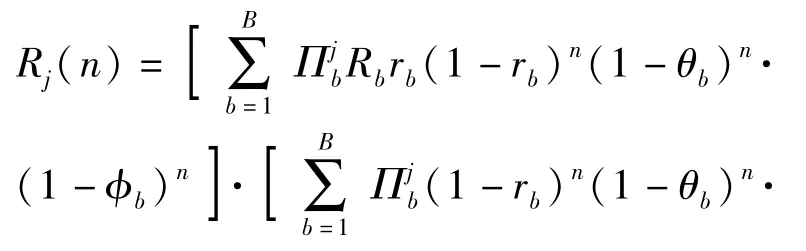
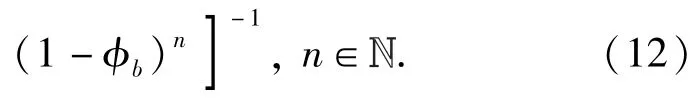
由（8）式知，射擊戰斗還需一個終止時刻，即過程｛Xj（t），t≥0｝有一個固定的終止集合。令τr（r為正整數，Xj（0）=n）為紅方射擊的終止時刻，紅方對藍方目標j能射擊r次，直到二者之間有一個被摧毀時停止射擊。隨機變量τr表示當前紅方射擊次數，則紅方所有射擊行動的期望收益為

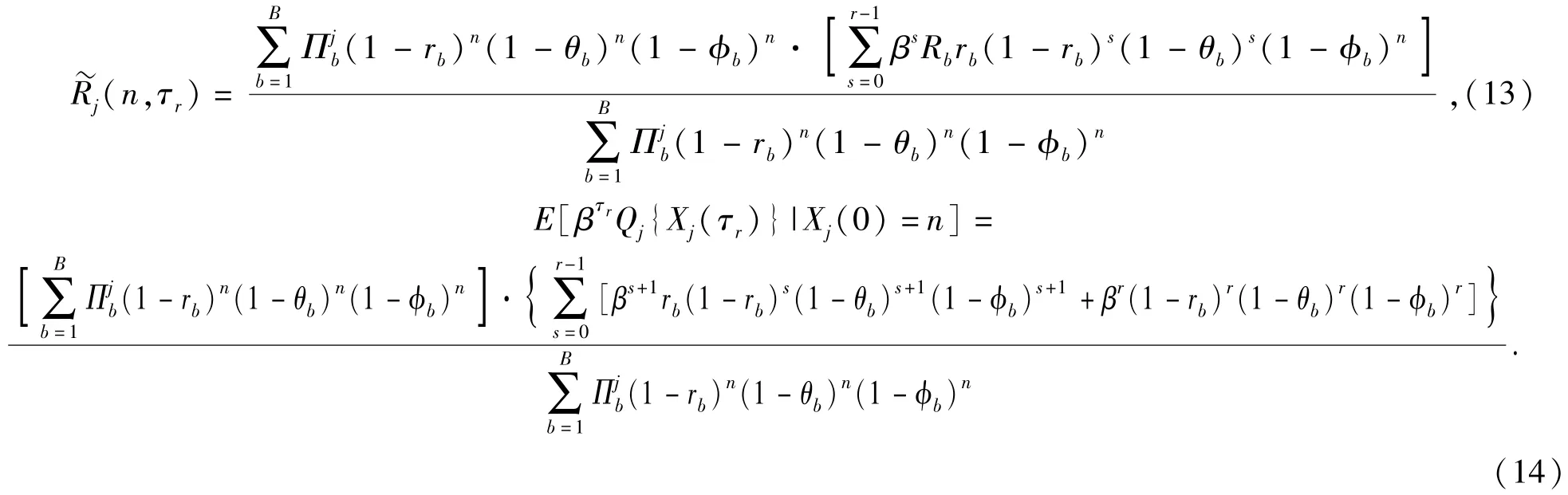
定理2 假設在t時刻紅方未被摧毀，紅方射擊藍方目標j*是最優策略，當j*滿足（15）式時成立：

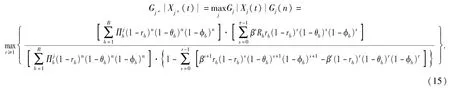
令（15）式中r=1，則可將Gj（n）化為Hj（n）（即僅當前考慮射擊收益，不考慮后續射擊收益）：

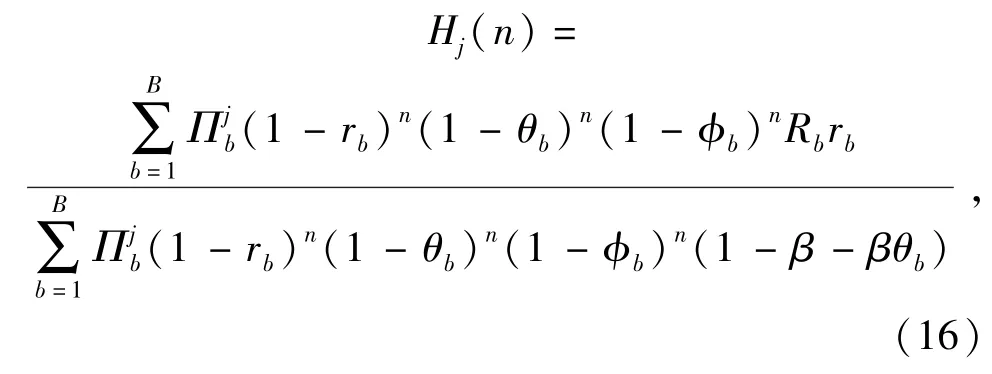
式中：Hj（n）本質上可被理解為紅方射擊藍方b類型目標（服從后驗概率分布）的加權平均收益指數Rbrb（1-β+βθb）-1.當Rb和rb較大、θb較小時，收益指數較高，即目標價值和紅方殺傷概率較大，被其摧毀概率較小時收益指數較高，較適合射擊；反之，對于Rb和rb較小、θb較大的目標，即目標價值和紅方殺傷概率較小，被其摧毀概率較大時收益指數較低，不適合射擊，上述分析與實際作戰認知也較為相符。此外需注意，概率θb可能會隨著紅方干擾和機動措施的實施而減小。

定理2給出了紅藍雙方射擊對抗采用指數策略的計算公式，如果Hj（n）是單調遞減的，則當r=1時，對于所有n，（16）式取得最大值，此時Gj（n）= Hj（n），n∈?，這種極端情況表示紅方最優策略是不斷轉換射擊的藍方目標，選擇射擊指數最高的目標射擊；如果函數Hj（n）是單調遞增的，則當r→∞時，對于所有n，（16）式取得最大值，此時

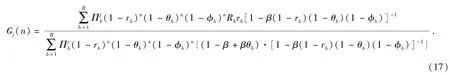
這種極端情況表示紅方最優策略是對每一個藍方目標持續射擊直至目標被殺傷。

當藍方目標只有兩種類型時（B=2），可得推論1.

推論 對所有n，當B=2時Hj（n）必然是單調遞減（單調遞增）函數。

證明 當B=2時，存在

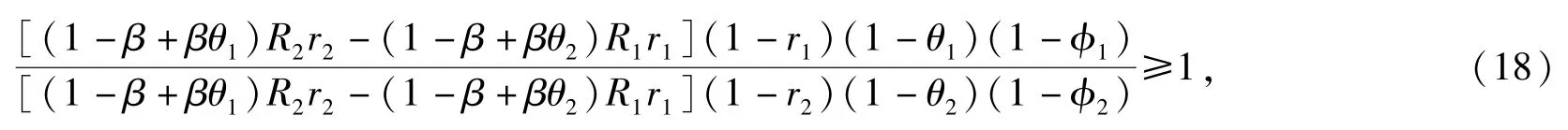
（18）式的成立顯然不依賴j、n，則對于所有j、n∈?必有

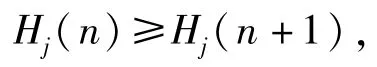
此時Hj（n）是單調遞減函數。同理，可證Hj（n）也可是單調遞增函數，推論成立。

推論是一種特殊情況，當藍方目標類型有兩種時，紅方總是由射擊類型1目標轉向射擊類型兩目標或由射擊類型2目標轉向射擊類型1目標，這是隨著射擊指數遞增或遞減時的最優決策，其本質上是基于類型1或類型2誰擁有更高的射擊指數而選擇對誰進行射擊。

4 近視策略、完全策略和循環策略

4.1 近視策略

如果指數策略選擇射擊目標是考慮射擊戰斗的長遠期望收益，那么近視策略選擇射擊目標則是考慮即時最優收益，因此近視策略又可稱為即時最優策略。近視策略指導紅方決策者按“眼前”最優收益進行射擊。如果藍方目標j為b類型的先驗概率分布為，采用近視射擊策略，進行n次射擊戰斗后收益為

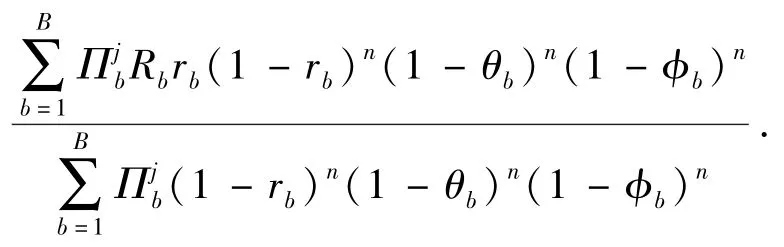
近視策略并不一定是最優策略［16］，如某次射擊戰斗，有兩枚射擊彈，射擊兩個目標，兩枚射擊彈對兩個目標的殺傷概率為［1，0.9；0.9，0］，R1= R2=1.采用近視策略，則用第1枚選擇目標1，不會使用第2枚射擊彈，總收益是1；而最優的射擊策略則是用第2枚射擊目標1，如果失敗再用第1枚射擊目標1，或第1枚射擊目標2，總收益是0.9×（1+0.9）+0.1×（0+1）=1.81，顯然這個例子說明了近視策略并非最優策略。對本文研究來說，近視策略以紅方當前時刻收益最大為目標，計算量小，實時性強，但未考慮下一時刻目標類型的變化對射擊收益的影響，適用常規目標無差別射擊。很多情況下相比指數策略，近視策略可以稱之為一種次優策略。

定理3 如果紅方采用近視射擊策略，可以最大化對藍方目標的期望殺傷數量。

證明 由（11）式可知，對目標進行射擊后會出現紅方和藍方目標j均存活、紅方存活而藍方目標j被殺傷、紅方被摧毀及紅方和藍方目標j均存活且藍方目標j退出戰斗4種情況。4種情況期望收益Rj（n）和紅方所有射擊行動的期望收益分別為

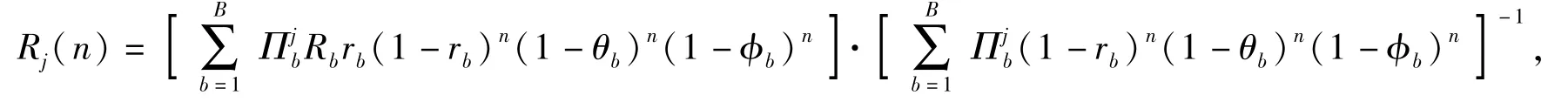
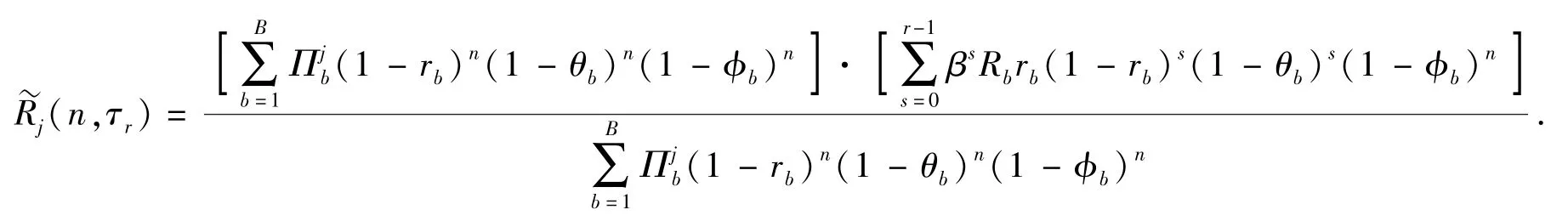
令β=1，Rb=1，r=1，可得

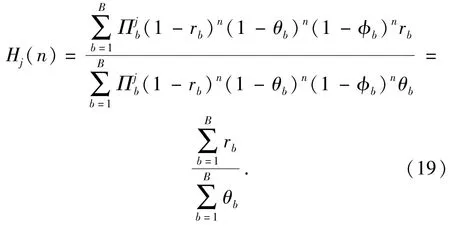
（19）式結合近視策略的定義，看出對于每個類型藍方目標來說，在目標價值不變的情況下，近視策略不考慮后續射擊收益，總是選擇當前“最容易殺傷”的藍方目標進行攔截，顯然可以最大化對藍方目標的期望殺傷數量，定理3成立。

4.2 完全策略

完全射擊策略就是紅方對每一個藍方目標持續射擊，直至目標被殺傷或自己被摧毀［17］。這種射擊策略需要對目標進行簡單排序，也可轉化為多臂bandit問題。如N=10時，紅方射擊藍方目標的次序可按照（20）式從高到低排序：

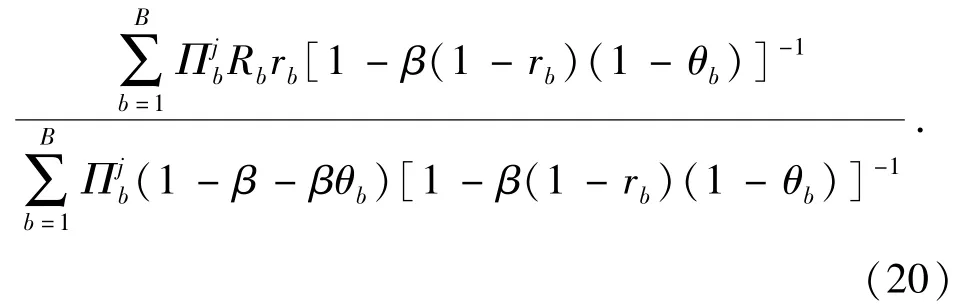
4.3 循環策略

循環射擊策略就是對存活待射擊的藍方目標，紅方按某種順序循環射擊（如目標編號從小到達），第1個射擊目標隨機選擇。

5 實例分析

參數設置：設計兩個射擊戰斗場景，均含有10個待射擊藍方目標，藍方目標有5種類型，具體參數如表1所示。

由表1可見，基本上藍方價值越高的目標就越難被殺傷，且紅方被摧毀的概率越大。已知N=10，B=5，每次計算將目標分成5組，設置組內第i類型目標先驗概率為0.75，組間設相互獨立，并服從U（0，1）分布，滿足，折扣率β設為0.95.

實驗過程：作為比較，采用4種射擊策略對兩個問題進行求解。針對4種射擊策略分別計算10000次。

實驗結果：實驗記錄了兩個場景紅方的收益，包括最小收益、平均收益、最大收益、收益的下四分位數、中位數、上四分位數、平均殺傷數量、紅方被摧毀概率等數據。四分位數是指將所有收益數值按大小順序排列并分成4等分，處于3個分割點的位置就是四分位數，最小的四分位數稱為下四分位數，以此類推。如表2所示為兩個場景下針對4種射擊策略紅藍雙方對抗紅方收益的數據匯總。如表3所示為兩個場景下針對4種射擊策略紅方殺傷藍方目標數量的數據匯總。如表4所示為4種射擊策略下紅方被摧毀的概率。如圖1所示為兩個場景下4種射擊策略射擊收益和平均殺傷數量對比。

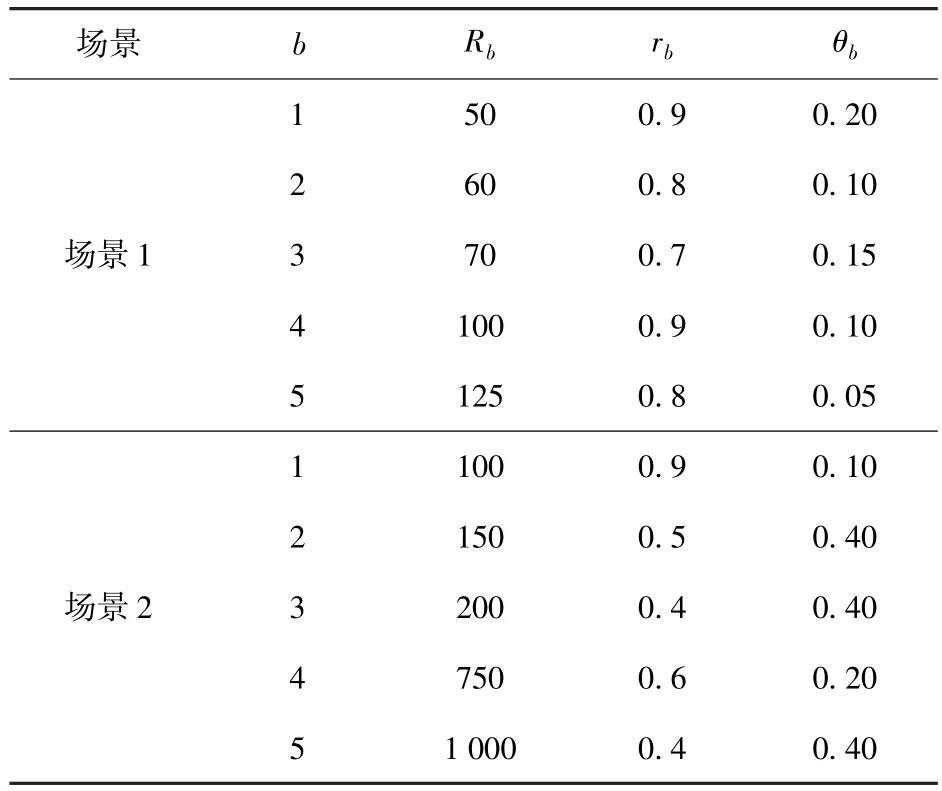
表1 紅藍雙方參數值Tab.1 Parameter values of red and blue sides

6 結論

一般認為，射擊戰斗過程中較好射擊策略是根據紅藍雙方當時狀態確定的，應當是即時最優策略（近視策略）；較差策略是完全策略和循環策略，因為這兩種策略不太考慮射擊收益，而通過實例和計算結果分析發現并非如此。4種射擊策略中指數策略要優于其他3種射擊策略，尤其是平均射擊總收益和平均殺傷藍方目標數量上具有優勢，與定理1和定理2的論述相符。近視策略比預想表現要差，其根本原因在于對紅方自身被摧毀的概率考慮較少，導致紅方較早被摧毀而結束戰斗，獲得的射擊總收益也較少。實例中，近視策略甚至還不如完全策略或循環策略，其原因值得下一步進行研究。

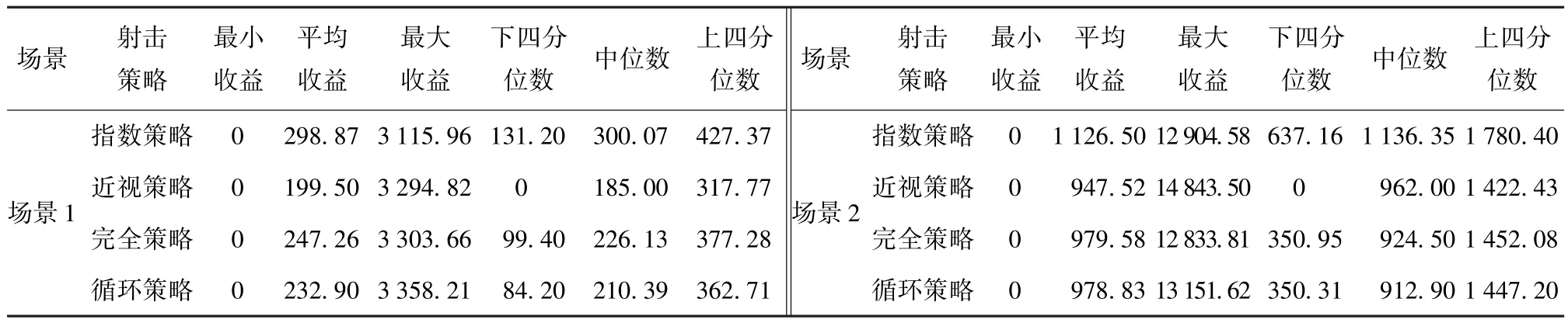
表2 紅方收益數據匯總Tab.2 Red's return

表3 紅方殺傷藍方目標數量數據匯總Tab.3 Summary of killed blue targets

表4 紅方被摧毀的概率Tab.4 Probability of the red being destroyed

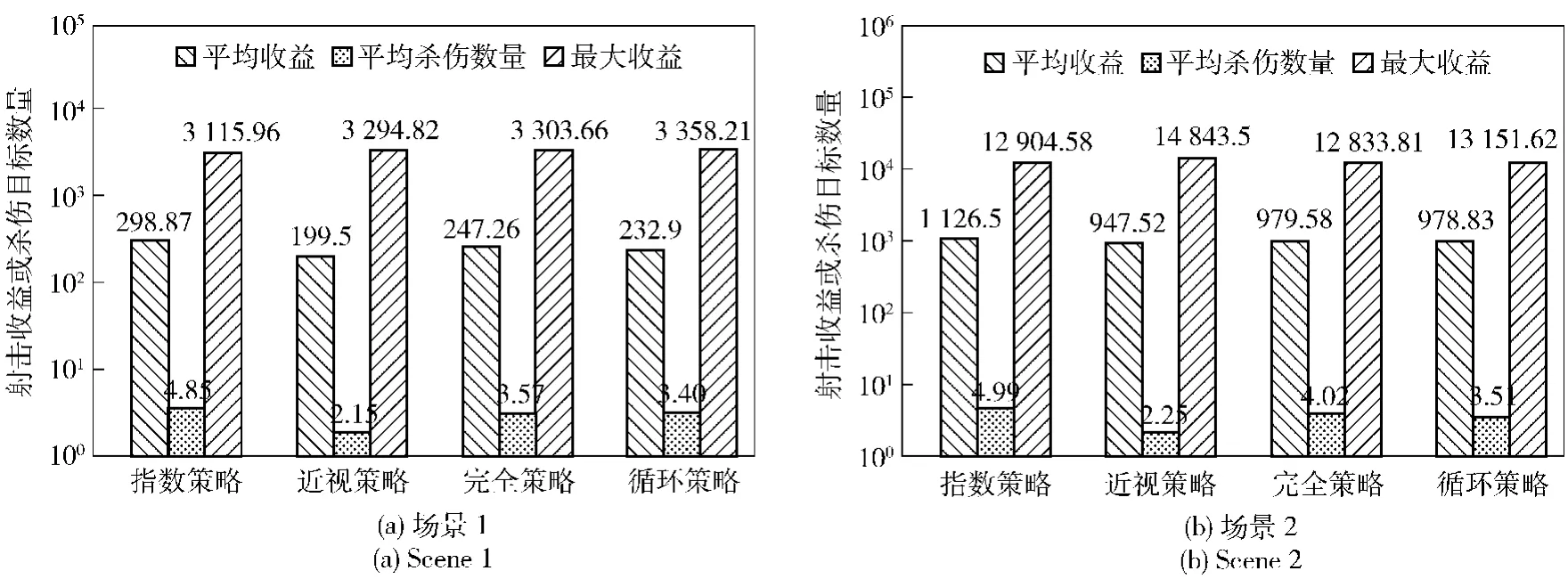
圖1 兩個場景下4種射擊策略射擊收益和平均殺傷數量對比Fig.1 Shooting returns and mean killing numbers of 4 shooting policies in 2 scenes

（

）

［1］滕克難，盛安冬.艦艇編隊協同反導作戰網絡效果度量方法研究［J］.兵工學報，2010，31（9）：1247-1253. TENG Ke-nan，SHENG An-dong.Research on metric of network effect in ship formation cooperation anti-missile operation［J］.Acta Armamentarii，2010，31（9）：1247-1253.（in Chinese）

［2］符小衛，李金亮，高曉光.防空威脅聯網建模與分析［J］.兵工學報，2013，34（7）：904-909. FU Xiao-wei，LI Jin-liang，GAO Xiao-guang.Modeling and analy-zing of air-defense threat netting［J］.Acta Armamentarii，2013，34（7）：904-909.（in Chinese）

［3］Gittins J C.Multi-armed bandit allocation indices［M］.Chichester：Wiley，1989.

［4］Anderson C M.Ambiguity aversion in multi-armed bandit problems［J］.Theory and Decision，2012，72（1）：15-33.

［5］Gu M Z，Lu X W.The expected asymptotical ratio for preemptive stochastic online problem［J］.Theoretical Computer Science，2013，495：96-112.

［6］Sonin I M.A generalized Gittins index for a Markov chain and its recursive calculation［J］.Statistics and Probability Letters，2008，78（12）：1526-1553.

［7］Kumar U D，Saranga H.Optimal selection of obsolescence mitigation strategies using a restless bandit model［J］.European Journal of Operational Research，2010，200（1）：170-180.

［8］Si P B，Ji H，Yu F R.Optimal network selection in heterogeneous wireless multimedia networks［J］.Wireless Networks，2010，16（5）：1277-1288.

［9］Glazebrook K D，Gaver D P，Jacobs P A.On a military scheduling problem［R］.Monterey CA：Naval Postgraduate School，2001.

［10］Barkdoll T C，Gaver D P，Glazebrook K D，et al.Suppression of enemy air defense（SEAD）as an information duel［D］.Monterey：Naval Postgraduate School，2001.

［11］Glazebrook K D，Washburn A.Shoot-look-shoot：a review and extension［J］.Operations Research，2004，52（3）：454-463.

［12］Barkdoll T C，Gaver D P.Suppression of enemy air defences（SEAD）as an information duel［J］.Naval Research Logistics，2002，49（8）：723-742.

［13］Glazebrook K D，Mitchell H M，Gaver D P，et al.The analysis of shooting problems via generalized bandits［R］.Monterey CA：Naval Postgraduate School，2004.

［14］Glazebrook K D，Kirkbride C，Mitchell H M，et al.Index policies for shooting problems［R］.Monterey CA：Naval Postgraduate School，2006.

［15］Nash P.A generalized bandit problem［J］.Journal of the Royal Statistical Society：Series B，1980，42（2）：165-169.

［16］Glazebrook K D，Greatrix S.On transforming an index for generalized bandit problems［J］.Journal of Applied Probability，1995，32（1）：168-182.

［17］Xu N X.Optimal policy for a dynamic，non-stationary，stochastic inventory problem with capacity commitment［J］.European Journal of Operational Research，2009，199（2）：400-408.

Optimality Analysis of Index Policy for Offense-defense Shooting Process

LI Long-yue，LIU Fu-xian，ZHAO Lin-feng，WANG Dong-xu
（Air and Missile Defense College，Air Force Engineering University，Xi'an 710051，Shaanxi，China）

The index policy for offense-defense shooting process，namely，how a single red shoots at a collection of blue targets to maximize the return obtained from killed blue targets，is discussed.In consideration of the limitations of previous research and the balance of the red's excepted return and survival probability，Gittins index is introduced and expanded to solve the shooting problems.The optimality of index shooting policy is discussed.Theorem 1 and 2 are extended，and Lemma 1 is presented.Three different shooting policies，such as myopic policy，exhaustive policy and round-robin policy，are introduced for comparison，and the optimality theorem 3 of myopic policy is proposed.2 shooting scenes are set in numerical study.The red's mean return，mean numbers of killed blue targets and red's death rate are calculated for 4 policies.Simulation study outcome verified the optimality of index policy.

ordnance science and technology；shooting policy；Gittins index；index policy；myopic policy

E917

A

1000-1093（2015）05-0953-08

10.3969/j.issn.1000-1093.2015.05.028

2014-06-05

全軍軍事學研究生課題項目（2014年）

李龍躍（1988—），男，博士研究生。E-mail：lilong_yue@126.com；劉付顯（1962—），男，教授，博士生導師。E-mail：liuxqh@126.com