半捷聯慣導系統軸向角度安裝誤差分析與補償

張樨，李杰，侯利朋，祝敬德，秦麗

（中北大學儀器與電子學院，山西太原030051）

半捷聯慣導系統軸向角度安裝誤差分析與補償

張樨，李杰，侯利朋，祝敬德，秦麗

（中北大學儀器與電子學院，山西太原030051）

針對半捷聯慣性測量系統中軸向角度安裝誤差影響系統姿態測量精度的問題，分析了軸向角度安裝誤差的來源、產生機理及其對姿態測量精度的影響規律，并從理論上推導了其數學表達式。在此基礎上，提出了軸向角度安裝誤差的分級補償方法。該方法的核心思想是，根據軸向角度安裝誤差產生的原理和作用機理不同，依次對其補償。地面實測試驗表明，對軸向角度安裝誤差的補償方法是正確和有效的，利用該補償方法可以將軸向角度安裝誤差引起的周期性姿態測量誤差由0.32°減小到0.05°以內，減小幅度達1個數量級，顯著地提高了系統的解算精度。

兵器科學與技術；半捷聯；慣性測量系統；角度安裝誤差；分析；補償

0 引言

基于微機電（MEMS）慣性器件的慣性測量系統由于具有自主性強、可靠性高、體積小、質量輕、成本低、功耗小、抗高過載以及易于安裝和維護等一系列的優勢，被認為是空間狹窄、環境惡劣、飛行時間較短的旋轉彈藥制導化過程中不可或缺的重要導航制導組件［1-3］。然而由于制造工藝的限制，MEMS慣性元器件存在量程和測量精度之間的矛盾，從而導致傳統的捷聯式測量方法在高轉速環境下測量精度降低［4-5］。半捷聯式測量方法基于滾轉軸隔離原理，能夠為慣性測量單元提供減旋環境，使小量程、高精度的MEMS慣性器件得以應用，有利于提高制導彈藥的測量精度，進而提高其打擊精度［6-9］。

半捷聯慣性測量系統涉及到各組件之間的軸向裝配問題，因此不可避免地會引入軸向角度安裝誤差，進而在系統姿態測量過程中產生周期性的姿態誤差，導致慣性測量系統的姿態測量精度降低［10-11］。本文針對系統中存在的軸向角度安裝誤差問題，對其進行了理論分析和數學建模，進而提出了補償該誤差的方法與措施，并通過地面實測試驗驗證了該方法的正確性和有效性。

1 半捷聯慣性測量系統組成結構與工作原理

半捷聯慣性測量系統主要分為系統、內筒、支撐結構（包括支撐軸和支撐軸承）和角度測量裝置（光電編碼器）四部分，如圖1所示。

圖1 半捷聯慣性測量系統結構Fig.1 Structure of semi-strapdown INS

MEMS慣性測量單元（MIMU）安裝在系統的內筒之中，內筒通過支撐軸與系統連接，并且可以通過支撐軸承在滾轉軸向上自由轉動，而另外兩個方向上與系統捷聯。通過配置偏心質量塊使內筒重心偏移，因此在系統隨旋轉彈藥旋轉時，內筒由于受到重力力矩的作用（軸承的摩擦力矩與重力力矩相比很小，故忽略不計）而不隨外部彈體旋轉，從而大大降低了內筒的實際滾轉角速度，有效地達到“滾轉隔離”的效果。絕對式光電編碼器測量內筒與系統之間的相對轉動角度，為內筒到系統的姿態信息變換提供相對轉動角度信息。

由于半捷聯裝置可以有效降低內筒的滾轉角速度，從而可以應用較低量程、較高精度的MEMS慣性器件（尤其是MEMS陀螺儀），從器件方面進一步提高了姿態、位置信息測量精度。

與捷聯系統相比，半捷聯慣性測量系統在軸向上的組成部件更多，因此裝配過程中會引入更多的軸向角度安裝誤差。這些角度誤差相互疊加，為誤差的分析與補償帶來困難。因此本文主要研究多個軸向角度安裝誤差疊加對姿態信息的影響，以及補償該誤差的方法。

2 軸向角度誤差產生機理分析

如圖2所示，定義系統坐標系為O0x0y0z0，其中O0為系統安裝面的中心，x0軸沿系統軸向前，y0軸垂直于系統軸向上，z0軸與x0軸和y0軸構成右手坐標系，坐標系隨系統轉動；內筒坐標系為O1x1y1z1，其中O1為內筒底面的圓心，x1軸沿內筒軸向前，y1軸垂直于內筒軸向上，z1軸與x1軸和y1軸構成右手坐標系，坐標系隨著內筒轉動；MIMU的坐標系為O2x2y2z2，隨著MIMU轉動。由于上述各部件之間存在軸向配合關系，所以不可避免地會引入軸向角度安裝誤差。

圖2 坐標系定義Fig.2 Definition of coordinate system

由于內筒與系統之間存在角度安裝誤差，故當系統繞x0軸以角速度ω0轉動時，會帶動內筒軸x1繞x0軸做錐運動，與此同時，內筒受到軸承的摩擦力矩與自身重力力矩的共同作用，繞自身x1軸以角速度ω1做小幅度擺動（小于±5°），故內筒的實際運動由錐運動和自身擺動復合而成。

由于內筒繞系統軸做錐運動，故設定內筒與系統之間的軸向角度安裝誤差為半錐角α；內筒與MIMU之間無相對轉動，故設定內筒與MIMU之間的角度安裝誤差為（ψ0，θ0，0）.

經上述分析，當系統以角速度ω0轉動，內筒以角速度ω1做小幅度擺動時，可將內筒實際的三軸角速度（ωx1，ωy1，ωz1）T表示如下:

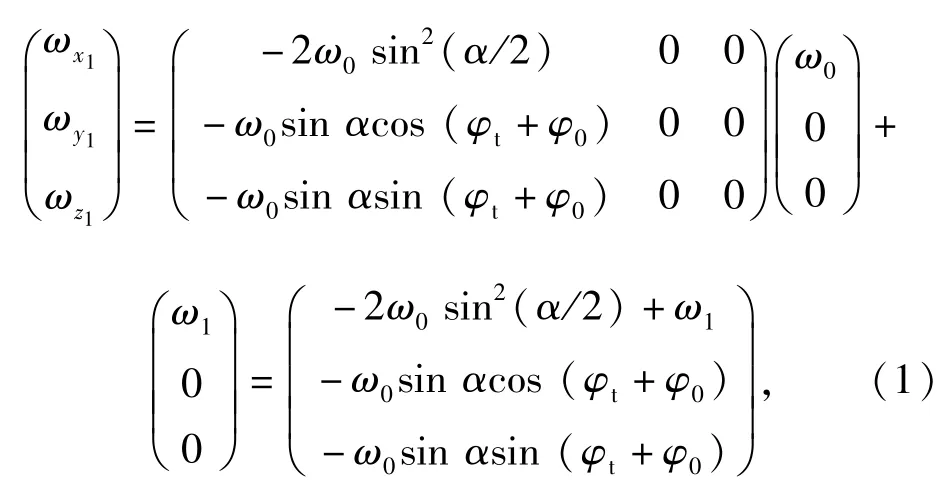
式中:φt為光電編碼器測得的內筒與系統之間的相對滾轉角度；φ0為內筒與系統之間的初始滾轉角度。

由于內筒與MIMU之間的軸向角度安裝誤差為（ψ0，θ0，0），根據坐標變換原理，可求得此時MIMU測量到的角速度分量（ωx2，ωy2，ωz2）T為

式中:

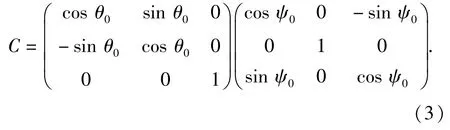
3 軸向角度誤差補償方法

3.1 MIMU與內筒之間的角度安裝誤差計算方法

將內筒固定到高精度速率轉臺上，并通過校正確保內筒與轉臺同軸，當轉臺帶動內筒以角速度（ω1，0，0）T轉動時，MIMU會相應地測量到三軸角速度為（tlx1，tly1，tlz1）T，假設內筒與MIMU之間的軸向角度安裝誤差為（ψ0，θ0，0），則根據（2）式和（3）式可建立如下關系式:

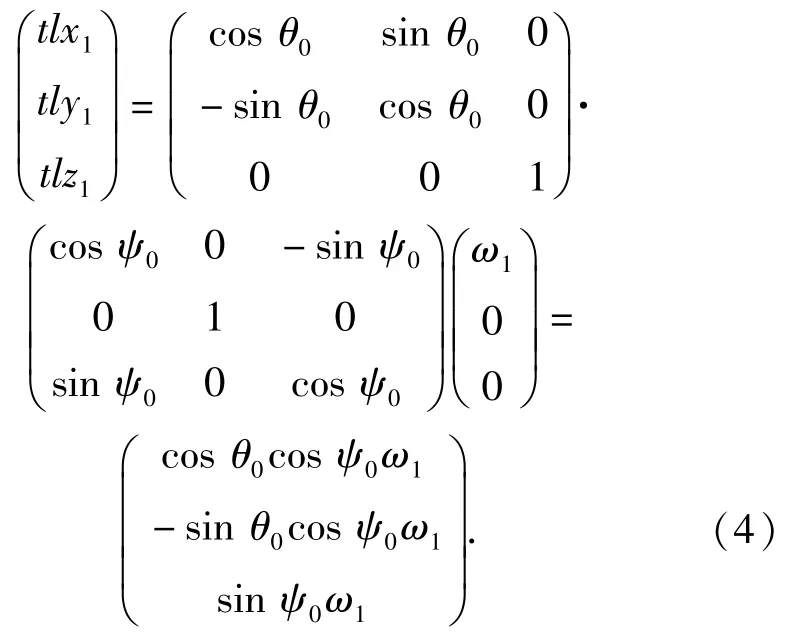
由（4）式可提取出ψ0和θ0的表達式分別為

3.2 內筒與系統之間的角度安裝誤差計算方法

將慣性測量系統固定在飛行仿真轉臺上，并通過校正確保慣性測量系統與轉臺同軸。飛行仿真轉臺以角速度ω0帶動系統轉動，可測得MIMU的三軸角速度（tlx2，tly2，tlz2）T，由（2）式可推導出內筒的三軸角速度信息（ωx1，ωy1，ωz1）T，如（5）式所示。

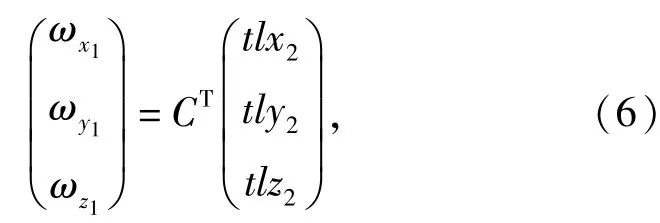
式中:

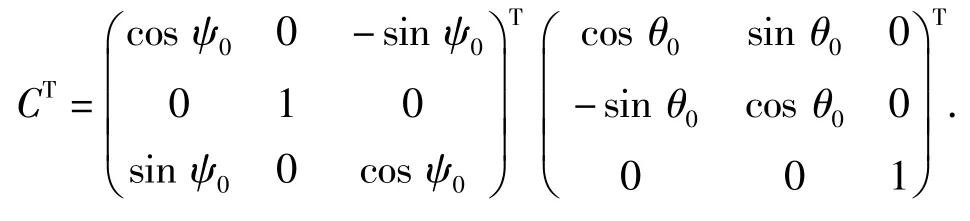
根據（1）式可提取出以下等式:

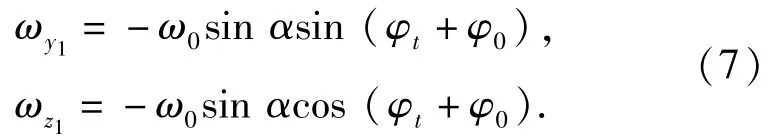
解此二元方程可得內筒與系統之間的軸向角度安裝誤差α以及內筒與系統之間的初始滾轉角度φ0:

3.3 角度誤差補償方法

角度誤差補償的最終目的就是去除角速度測量信息中由軸向角度安裝誤差引入的姿態誤差信息。

第一步，將MIMU測量到的角速度信息（tlx，tly，tlz）T通過坐標變換投影到內筒坐標系，則可計算出內筒的角速度信息為

通過該步可消除MIMU與內筒之間角度安裝誤差對角速度測量誤差的影響。

第二步，去除內筒角速度信息中由圓錐運動引起的角速度誤差信息，則可得到內筒在去除圓錐運動誤差影響后的角速度為

式中:ω0為系統角速度信息（內筒軸向角速度為ωx1，對光電編碼器測得的角度信息使用M/T法可求得內筒與系統之間的相對轉動角速度ωx1-x0，二者疊加即可得出ω0.

4 試驗驗證

為了驗證該補償方法的正確性，設計了角度誤差標定與補償試驗。該試驗采用零偏穩定性為30°/h，量程為±300°/s的MEMS陀螺儀組成慣性測量單元，通過相應試驗求得角度誤差（ψ0，θ0，0）和α，再通過上述分析方法進行誤差補償。

4.1 求取角度誤差（ψ0，θ0，0）

高精度速率轉臺帶動內筒以280°/s的恒定角速度轉動，MIMU測量到的三軸角速度tlx1、tly1、tlz1信息如圖3所示。

圖3 MIMU角速度信息Fig.3 Angular velocity information from MIMU

將三軸角速度代入（5）式可計算出:ψ0= -0.11°，θ0=-0.04°.

4.2 求取角度誤差α

在飛行仿真轉臺上以角速度6 480°/s帶動系統轉動，由MIMU測量到的三軸角速度，經過（9）式所示的坐標轉換后，可得到內筒的三軸角速度ωx1、ωy1、ωz1信息，如圖4所示。

圖4 內筒角速度信息Fig.4 Angular velocity information of internal cylinder

將內筒的三軸角速度代入（8）式可得:α= 0.164 2°，φ0=27.3°.

4.3 角度誤差補償

以半捷聯慣性測量系統為對象進行角速度實測試驗。角速度轉臺帶動內筒以3 600°/s轉動，轉動時間為60 s，采集MIMU的角速度信息，分別用未補償和補償后的角速度信息進行姿態解算，并對這兩種情況下得到的姿態信息進行對比分析。

MIMU測量到的原始轉速ωx2、ωy2、ωz2信息如圖5所示。解算出來的系統姿態ψ′、θ′、γ′信息如圖6所示。

由圖5可看出，由于軸向角度安裝誤差的存在，當系統繞x0軸轉動時，MIMU的y軸和z軸上敏感到幅度約為10°/s的周期角速度信號。

由圖6可以看出，由于存在軸向角度安裝誤差，導致偏航角和俯仰角信息中存在寬度約為0.32°的誤差信號，導致系統的姿態測量精度下降。

偏航角信息的邊緣局部放大圖如圖7所示。

由圖7可以看出，偏航角姿態信息中的誤差信號由兩個周期信號疊加而成。經過對偏航信息進行頻譜分析得到對應的頻譜圖，如圖8所示。

圖5 未補償的轉速信息Fig.5 Speed information without compensation

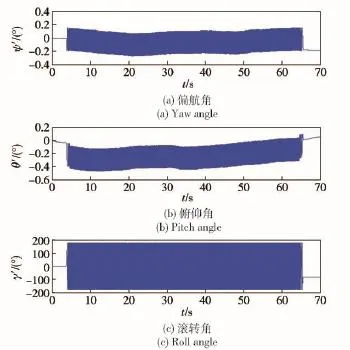
圖6 未補償的姿態信息Fig.6 Attitude information without compensation

圖7 偏航角信息邊緣局部放大圖Fig.7 Partially enlarged detail of yaw angle information

圖8 俯仰信號的頻譜圖Fig.8 Signal spectrum of pitching angle

由圖8可看出，俯仰信號的頻率分量主要集中在0 Hz、1.7 Hz和10 Hz.經對比分析表明:0 Hz代表偏航信息中的直流分量；1.7 Hz的周期誤差信號與內筒擺動頻率相同，是在內筒擺動過程中，由內筒與MIMU之間的角度安裝誤差引入的；10 Hz的周期誤差信號與系統轉動頻率相同，是由前文所述的錐運動引起。

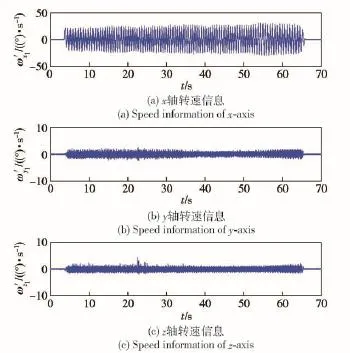
圖9 補償后的轉速信息Fig.9 Speed information with compensation

由圖9可看出，補償后，系統y軸和z軸上的角速度信息幅度由補償前的10°減小到1.5°.

圖10 補償后的姿態信息Fig.10 Attitude information with compensation

由圖10可看出，偏航角和俯仰角的周期性測量誤差從補償前的0.32°減小到補償后的0.05°，減小幅度達到1個數量級，顯著地提高了慣性測量系統姿態測量精度。

5 結論

本文基于對半捷聯慣性測量系統軸向角度安裝誤差對姿態信息影響的分析，提出了分級補償的方法。地面實測試驗驗證了該理論分析和補償方法的正確性和有效性。通過對補償前后的角速度信息和姿態解算信息進行分析比較表明，該補償方法可將姿態信息中偏航角和俯仰角的信號寬度由補償前的0.32°減小到0.05°，有效提高了慣性測量系統的姿態測量精度。

（

）

［1］ 李杰，趙詣，劉俊，等.高旋彈藥飛行姿態測量用半捷聯MEMS慣性測量裝置研究［J］.兵工學報，2013，34（11）:1398-1403. LI Jie，ZHAO Yi，LIU Jun，et al.Research on semi-strapdown MEMS inertial measurement device for flight attitude measurement of high-speed rotating ammunition［J］.Acta Armamentarii，2013，34（11）:1398-1403.（in Chinese）

［2］ 鮑亞琪，陳國光，吳坤，等.基于磁強計和MEMS陀螺的彈箭全姿態探測［J］.兵工學報，2008，29（10）:1227-1231. BAO Ya-qi，CHEN Guo-guang，WU Kun，et al.Research on attitude determination using magnetometers and MEMS inertial sensors［J］. Acta Armamentarii，2008，29（10）:1227-1231.（in Chinese）

［3］ 中北大學.一種適用于高旋彈藥的主動式半捷聯慣性測量裝置:中國，201110025530［P］.2011-08-17. North University of China.One for the high-spin ammunition semiactive strapdown inertial measurement unit:China，201110025530［P］.2011-08-17.（in Chinese）

［4］ 高峰，張合.基于基準角和補償角的常規彈藥滾轉角磁探測算法研究［J］.探測與控制學報，2008，30（5）:11-15. GAO Feng，ZHANG He.Algorithm of roll angle determination of conventional ammunitions based on benchmark angle and compensation angle［J］.Journal of Detection&Control，2008，30（5）: 11-15.（in Chinese）

［5］ 趙巖，程烘炳，吳訓忠，等.基于MEMS的低成本SINS/GPS組合導航系統研究［J］.傳感器與微系統，2011，30（8）:18-21. ZHAO Yan，CHENG Hong-bing，WU Xun-zhong，et al.Study on low cost SINS/GPS integrated navigation system based on MEMS［J］.Transducer and Microsystem Technologies，2011，30（8）: 18-21.（in Chinese）

［6］ 張松，李杰，趙詣，等.半捷聯MEMS慣性測量裝置數據硬回收系統設計［J］.傳感技術學報，2013，26（9）:1219-1223. ZHANG Song，LI Jie，ZHAO Yi，et al.Design of acquisition and storage system on half-strapdown system［J］.Chinese Journal of Sensors and Actuators，2013，26（9）:1219-1223.（in Chinese）

［7］ 蔣巍巍.基于MEMS的導航系統的初始對準及其相關問題研究［D］.沈陽:沈陽理工大學，2013. JIANG Wei-wei.Based on MEMS research on initial alignment in navigation system and its associated problems［D］.Shenyang: Shenyang Ligong University，2013.（in Chinese）

［8］ 梁勇.基于MEMS的航姿系統的設計與實現［D］.哈爾濱:哈爾濱工程大學，2011. LIANG Yong.The design and implementation of navigation posture system based on the MEMS［D］.Harbin:Harbin Engineering University，2011.（in Chinese）

［9］ 牛春峰，劉世平，王中原.制導炮彈飛行姿態的卡爾曼濾波估計方法［J］.中國慣性技術學報，2012，20（5）:510-514. NIU Chun-feng，LIU Shi-ping，WANG Zhong-yuan.Approach of Kalman filtering estimation of guided projectile attitude［J］.Journal of Chinese Inertial Technology，2012，20（5）:510-514.（in Chinese）

［10］ 程向紅，黃華.捷聯慣性系統初始對準中IMU安裝誤差及陀螺漂移的估計與補償［J］.中國慣性技術學報，2005，12（5）:13-15. CHENG Xiang-hong，HUANG Hua.Estimatin and compensation of IMU misalignment and gyros drifts during SINS initial alignment［J］.Journal of Chinese Inertial Technology，2005，12（5）: 13-15.（in Chinese）

［11］ 趙長山，秦永元，夏家和.車載慣導里程儀組合導航系統安裝誤差標定研究［J］.計算機測量與控制，2008，16（10）:1393-1395. ZHAO Chang-shan，QIN Yong-yuan，XIA Jia-he.On SINS installation error of a multimode vehicular navigation system［J］. Computer Measurement&Control，2008，16（10）:1393-1395.（in Chinese）

Analysis and Compensation of Installlation Axial Angle Errors of Semi-strapdown IMS

ZHANG Xi，LI Jie，HOU Li-peng，ZHU Jing-de，QIN Li
（School of Instrument and Electronics，North University of China，Taiyuan 030051，Shanxi，China）

The source and gemeration mechanism of installation axial angle errors of semi-strapdown inertial measurement system（IMS）and their effects on the attitude measuring accuracy are analyzed，and the mathematical expression of the influence is theoretically derived.A graded compensation method is proposed for error compensation.The proposed method is used to compensate the installation angle errors in turn according to their generation principle and effect mechanism.Experiment based on semi-strapdown IMS verified the validity and effectiveness of the method.Experimental results show that the method can effectively reduce the periodic attitude measuring error caused by installation axial angle errors to 0.05°compared with that of 0.32°without compensation.

ordnance science and technology；semi-strapdown；inertial measurement system；installation angle error；analysis；compensation

TJ06；TJ013

A

1000-1093（2015）07-1222-06

10.3969/j.issn.1000-1093.2015.07.010

2014-06-20

國防基礎科研計劃項目（B3320132012）

張樨（1977—），女，講師，博士研究生，E-mail:zhangxi@nuc.edu.cn；李杰（1976—），男，教授，博士生導師，E-mail:lj7610@126.com