帶有Neumann邊界條件和非局部反應(yīng)項的非局部擴散方程的爆破

李佳賢，杜宛娟

(西華師范大學(xué) 數(shù)學(xué)與信息學(xué)院，四川 南充 637009)

0 引言和主要成果

本文主要研究以下非局部擴散問題的爆破現(xiàn)象

其中，α ＞0，Ω 是一個有界連通光滑區(qū)域，核函數(shù)J:RN→R 是一個具有緊支集的非負有界連續(xù)對稱函數(shù)初值u0(x)是非負，非平凡的有界函數(shù)．問題(1)經(jīng)常出現(xiàn)在人口密度、化學(xué)反應(yīng)和熱傳遞等物理模型中．比如u(x，t)可以表示單一種群在空間點x 和時間t 時的密度，J(x -y)可以看作是種群從位置y 轉(zhuǎn)移到位置x 的概率分布，卷積(J* u)(x，t)=表示個體從其他位置到達位置x 的速率，而則表示離開位置x 到達其他位置的速率．非局部反應(yīng)項J* eαu(x，t)表示了單一人口密度在區(qū)域Ω 內(nèi)呈指數(shù)增長．在考慮內(nèi)源的情況下，密度u滿足非局部擴散方程(1)．在問題(1)中，積分僅僅是在Ω 上進行的，而∫J(x - y)(u(y，t)- u(x，t))dy 考慮了個體到達或離開位置x 的情況，因此，把這種擴散僅僅限定在Ω 上進行，沒有個體進入或離開這個區(qū)域．從而問題(1)具有Neumann 邊界條件，參見文獻［1］．

近年來，具有ut=∫RNJ(x -y)u(y，t)dy -u(x，t)這種形式的非局部擴散問題，以及它的一些變式，被廣泛應(yīng)用于擴散問題的建模，可以參考文獻［2 -8］．

現(xiàn)在給出這篇文章的主要成果．

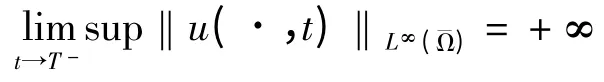
且在Ω 上滿足下面這個恒等式

確定了解的存在性和唯一性，接下來去研究解發(fā)生爆破時的時間和速度．

與之相關(guān)的爆破率，有:

定理3 假設(shè)u 是問題(1)的解，且在時刻T 爆破，則:

1 解的局部存在性

這部分主要給出定理1．1 的證明，并通過Banach 不動點定理來證明解的存在性和唯一性．為此，給出一些必要的準備．固定t0＞0，令Banach 空間其范數(shù)定義為:

定義算子T:Xt0→Xt0

問題(1)的解將在Xt0的一個適當?shù)那蛑校ㄟ^上面算子的一個不動點得出．將通過下面這個引理說明算子T 是有定義的，并且給出條件保證它是嚴格緊縮的．

引理1 算子T 是有定義的，且從Xt0映到Xt0．令那么，存在一個正常數(shù)C =C(α，‖w‖Xt0，‖z‖Xt0，K，Ω)，使得

若t0足夠小，則Tw0在球是嚴格緊縮的．

證明:首先驗證Tw0是從Xt0映到Xt0．對于有:

所以Tw0(w)在t=0 處連續(xù)．對于，滿足

則Tw0在(0，t0］上連續(xù)．

由于核函數(shù)J 在空間中是一致連續(xù)的，因此Tw0(w)是x 的連續(xù)函數(shù)．對則Tw0(w)于是Tw0(w)是從Xt0映到Xt0．

其中η≤max{‖w‖Xt0，‖z‖Xt0}．由(x，t)的任意性可得估計(4)式．

選取t0使得Ct0＜1，令w0=z0，那么在里，(4)式確保算子Tw0是嚴格緊縮的．實際上，w 和z 定義在這樣的球中可以得到因此，存在一個僅僅依賴于J 和u0的常數(shù)C，使得

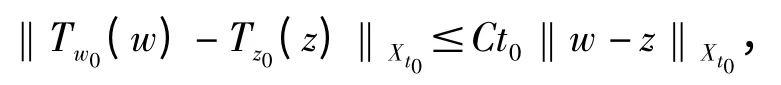
對此可以選取t0使得Ct0＜1/2 保證在球內(nèi)是嚴格緊縮的．

定理1 的證明(存在性與唯一性):由Banach 不動點定理和引理1 可以得到問題(1)的解在［0，t0］上是存在且唯一的．如果‖u‖Xt0＜∞，令初值對于t1＞t0，可以將解延拓到區(qū)間［0，t1)，和前面的證明類似．因此，若解存在一個最大時間T，是有限的，那么解在范數(shù)下爆破，即

從方程(1)中可以得到u 滿足下面的恒等式

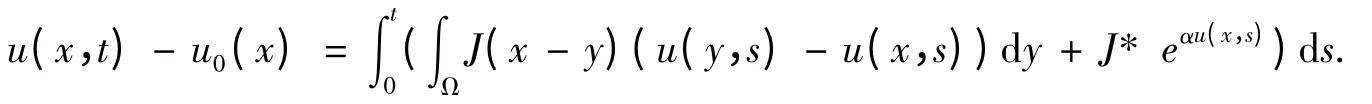
在等式兩邊對x 積分并運用Fubini 定理，則有

定理1 得證．

為了說明問題(1)的解滿足比較原理．為此，先介紹上解和下解．

下解的定義和上解的定義類似，只需將上面的≥全部換為≤．

現(xiàn)在給出與上解和下解有關(guān)的比較原理和極值定理兩個引理．證明參見文獻［9］．

2 爆破與爆破率

定理2 的證明:在方程(1)兩邊對x∈Ω 積分，運用Fubini 定理和Jensen 不等式，可得到:

所以∫Ωu(x，t)dx 不是全局存在的，則u 也不可能全局存在．通過定理1 可知，解u 在范數(shù)下爆破．在上式不等式積分中，可以得到對爆破時間的一個估計，即:

現(xiàn)在我們給出爆破率，即對定理3 進行證明．

對(5)式在(t，T)上積分，可得:

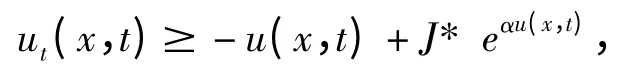
由于u(x，t)爆破，則存在t0使得對于任意的t∈(t0，T)，存在參數(shù)ε ＞0，使得

在(t，T)上積分，可得

令ε→0 時，由(6)和(7)式可得:

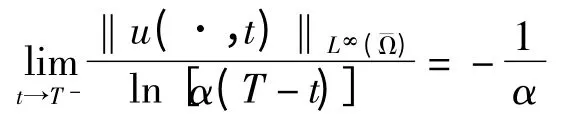
即定理得證．

［1］ CORTAZAR C，ELGUETA M，ROSSI J，et al． Boundary Uxes for Non-local Diffusion［J］． Journal of Differential Equations．2007，234(2):360 -390．

［2］ ANDREU F，MAZON J，ROSSI J，et al． The Neumann Problem for Nonlocal Nonlinear Diffusion［J］． Journal of Evolution Equations． 2008，8(1):189 -215．

［3］ ANDREU F，MAZON J，ROSSI J，et al． Local and Nonlocal Weighted P - Laplacian Evolution Equations with Neumann Boundary Conditions［J］． Publicacions Mathematiques． 2011，55(1):27 -66．

［4］ GALAKTIONOV V，VAZQUEZ J． The Problem of Blow -up in Nonlinear Parabolic Equations［J］． Discrete and Continuous Dynamical Systems． 2002，8(2):399 -434．

［5］ IGNAT L，PINASCO D，ROSSI J，et al． Decay Etimates for Nonlinear Nonlocal Diffusion Problems in The Whole Space［J］．Journal d'Analyse Mathematique． 2014，122(1):375 -401．

［6］ MAZON J，ROSSI J，TOLEDO J． On Nonlinear Nonlocal Diffusion Problems［J］． International Journal of Biomathematics ＆Biostatistics． 2010，1:181 -192．

［7］ SAMARSKI A，GALAKTIONOV V，KURDYUNOV S，et al． Blow -up in Quasilinear Parabolic Equations［M］． Walter de Gruyter，Berlin． 1995:560．

［8］ WANG M． Blow-up Rate Estimates for Semilinear Parabolic Systems［J］． Journal of Differential Equations． 2001，170(2):317 -324．

［9］ CORTAZAR C，ELGUETA M，ROSSI J，et al． How to Approximate The Heat Equation with Neumann Boundary Conditions by Nonlocal Diffusion Problems［J］． Archive for Rational Mechanics and Analysis． 2008，187(1):137 -156．