關于似星樹擬拉普拉斯譜的性質探討

程霄

（新疆農業大學 數理學院，新疆 烏魯木齊 830052）

關于似星樹擬拉普拉斯譜的性質探討

程霄

（新疆農業大學 數理學院，新疆 烏魯木齊 830052）

利用似星樹的簡單性質，結合偶圖的Laplacian譜和擬拉普拉斯譜的關系，得到了擬拉普拉斯同譜的似星樹同構的性質.進一步，通過矩陣的交錯理論，結合圖操作方法，得到了似星樹擬拉普拉斯譜的另一個性質.最后，根據其鄰接譜半徑的界，得到了似星樹的擬拉譜拉斯譜半徑的一個上界.

擬拉普拉斯矩陣特征值；似星樹；譜半徑；譜寬度

圖譜理論是代數圖論的重要研究領域.其中，圖的擬拉普拉斯譜問題在微分方程問題，矩陣理論，量子化學、生物學以及復雜網絡問題中有重要的應用，是目前研究的活躍問題.

本文討論的圖，均為簡單無向圖（不包括環和平行邊），未定義的概念在文［1］中都可以找到.設G=（V，E）是n階圖，其頂點集為V，點集為E.分別記D（G）=diag（du：u∈V）和A（G）= （auv）表示圖的度矩陣和鄰接矩陣.其中，du是頂點的度；當uv相鄰時，auv=1；否則，auv=0；鄰接矩陣的特征值記為λ1≥λ2≥…≥λn.圖G的Laplacian矩陣定義為L（G）=D（G）-A（G），其特征多項式為LG（x）.由于L（G）是一個實對稱半正定的奇異矩陣，故設其特征值為：μ1≥μ2≥…≥μn=0.圖的擬拉普拉斯（signlessLaplacian）矩陣Q（G）=D（G）+A（G），其特征多項式為QG（x）.由于A（G）是一個實對稱的、半正定的非負矩陣，則設其特征值為q1≥q2≥…≥qn≥0.

圖G的鄰接矩陣特征值、Laplacian矩陣特征值和擬拉普拉斯矩陣特征值都是圖的不變量.由于后兩個矩陣都加入了頂點的度，所以其特征值更能反映圖的性質.關于圖的譜半徑問題以及譜確定問題，一直以來都是前沿熱點問題.

似星樹（starlike tree）是一類特殊的樹圖，即只有一個頂點的度數大于2的樹.關于其鄰接譜半徑問題以及Laplacian譜確定問題研究，已經取得了大量的研究成果［3-5］.不過關于其擬拉普拉斯譜的性質的研究較少.

本文在已有的研究基礎上，通過矩陣理論、圖論的相關知識，結合圖操作等方法，進一步對似星樹的擬拉普拉斯特征值，譜半徑，譜寬度等問題進行探討，得到了一些結論.

1 基本理論

引理1［6］設n×n矩陣M和H，則下面的關系是等價的：

（1）M和H具有相同的譜；

（2）M和H具有相同的特征多項式；

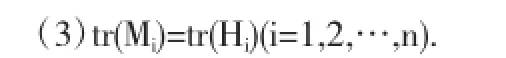
引理2［7］偶圖的擬拉普拉斯矩陣和Laplacian矩陣具有相同的特征多項式，即QG（x）=LG（x）

很多文獻提到過此定理，但沒給出詳細證明，其過程如下.

證明 設G是偶圖，兩部集的階數為n1，n2.結合分塊矩陣的理論，頂點按一定的順序標號，G的鄰接矩陣A可寫成

接下來，對LG（x）的前n1行和n1列分別都乘以-1，那正好得到QG（x），由此得證.

為了證明似星樹的擬拉普拉斯譜的性質，需要引入矩陣理論中的交錯原則.考慮兩個實數序列：

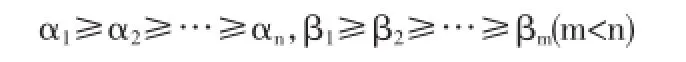
如果αi≥βi≥αn-m+i（i=1，2，…，m），則稱第二個序列交錯于第一個序列.

引理3［2］設S是一個n×m的實矩陣，滿足STS=I.同時，設A是一個n階實對稱矩陣，且特征值為α1≥α2≥…≥αn.定義B=STAS，其特征值為：β1≥β2≥…≥βm，那么B的特征值序列交錯于A的特征值序列.

在上述定理中，若令S=［I0］T，那么B就是A的一個主子陣，則有：

引理4［2］設B是對稱矩陣A的主子陣，則B的特征值序列交錯于A的特征值序列.

利用此引理，就能得到圖譜理論中相應的交錯定理.

引理5［8］（邊交錯定理）設圖G有n個頂點，m條邊.且e∈E（G），并設G的擬拉普拉斯特征值和G-e的擬拉普拉斯特征值分別為：q1≥q2≥…≥qn，s1≥s2≥…≥sn，那么：

0≤sn≤qn≤…≤s2≤q2≤s1≤q1

文獻［9］中，利用此引理，同時結合矩陣理論中的Wely's不等式和Cquchy交錯定理，得到了關于擬拉普拉斯特征值的點交錯定理.

引理6［9］（點交錯定理）設圖G為n階圖，頂點集為V （G），且v∈V（G），設G的擬拉普拉斯特征值和G-v的擬拉普拉斯特征值分別為q1（G）和qi（G-v），其中i=1，2，…，n.那么：

其中，右邊的等號成立，當且僅當v是孤立點.

為了討論似星樹的擬拉普拉斯譜半徑問題，需要引入以下定理：

引理7［8］若n階圖G至少有一條邊，設其最大度為Δ，那么：

若G是連通的，則當且僅當G是偶圖，有第一個等號成立；當且僅當=n-1.有第二個等號成立.

引理8［10］設G為n階圖，則有

其中，λ1是圖G的鄰接譜半徑；當且僅當G是正則的，等號成立.

2 主要結果

定義1［11］只有一個頂點的度數大于2的樹，稱為似星樹.記為S（n1，n2，…，nk），其中n1，n2，…，nk是正整數，n1≥n2≥…≥nk≥1，且頂點最大度為k（k≥3）.

定理1 如果兩棵似星樹S（n1，n2，…，nk）和S（m1，m2，…，mk）是擬拉普拉斯同譜圖，那么它們一定是同構的.

證明 文獻［12］中通過似星樹的線圖的性質，證明了只要兩棵似星樹是同譜的，則一定也是同構的.樹是一類特殊的偶圖，由引理2可知，偶圖的擬拉普拉斯譜等于其Laplacian譜，那么結論得證.

定理2 似星樹最多只有一個擬拉普拉斯特征值不小于5.

證明 由似星樹的定義，不妨設頂點v的度數為k，那么顯然它有下面的性質：

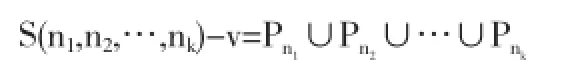
因此，q2（S）-1≤q1（S-v）≤q1（S），又因為q1（S-v）＜4，那么顯然q2（S）＜5.結論得證.

定理3 設q1是Starlike樹S（n1，n2，…，nk）的Q-譜半徑，且Δ是其最大度，那么對任意的n1≥n2≥…≥nk≥1，都有：

其中，n=n1+n2+…+nk+1，下界的等號成立，當且僅當n1=n2=…=nk=1，即G是星圖Sn.

證明 一方面，由邊交錯定理和引理7易得q1的下界.當且僅當n1=n2=…=nk=1時，G是星圖Sn，q1取得最小值.另一方面，由引理8可知，q1≤λ1+Δ，只要根據似星樹的鄰接譜半徑的界，便可找到q1的上界，在文獻［11］中，證明了似星樹S（n1，n2，…，nk）的鄰接譜半徑的一個界，即對任意的n1≥n2≥…≥nk≥1，都有：

由似星樹的定義可知，k是該圖的最大度，也即

綜上所述，結論得證.

對于擬拉普拉斯譜寬度的研究也是一個方向，通過上面的定理易得下面的結論.

推論 設SQ（S）是似星樹S（n1，n2，…，nk）的擬拉普拉斯譜寬度（即q1-qn）.且Δ是其最大度，那么對任意的n1≥n2≥…≥nk≥1，都有：

其中，n=n1+n2+…+nk+1，下界的等號成立，當且僅當n1=n2=…=nk=1，即G是星圖Sn.

3 結束語

針對一類特殊的圖——似星樹，得到了其部分擬拉普拉斯譜的性質.關于似星樹的擬拉普拉斯譜的研究，還值得深入討論，譜確定問題和頂點連通度問題仍是重要研究方向［13-14］.

〔1〕Bondy JA，Murty U S R.Graph theory with applications［M］.New York：Macmillan，1976.

〔2〕A.E.Brouwer，W.H.Haemers.Spectra of graphs［M］. Springer Verlag，2011.

〔3〕姚瑤，徐美進，楊文杰，等.最大度為4的似星樹的譜半徑［J］.遼寧工業大學學報（自然科學版），2014，34（01）：67-70.

〔4〕沈小玲.關于圖的譜確定問題［D］.長沙：湖南師范大學，2005.

〔5〕姚瑤.一類似星樹的譜半徑問題研究［D］.錦州：遼寧工業大學，2014.

〔6〕VANDRE，HAEMERSH W.Whichgraphsare determinedby their spectrum ［J］.Linear Algebra Appl.，2003，373：241-272.

〔7〕D.Cvetkovic，P.Rowlinson，S.K.Simic，Signless Laplacians of finite graphs［J］.Linear AlgebraAppl.，2007，423（1）：155-171.

〔8〕D.Cvetkovic，P.Rowlinson，S.K.Simic.Eigenvalue bounds for the signless Laplacian ［J］.Publ.Inst.Math（Beograd），2007，81（95）：11-27.

〔9〕J.F Wang，F.Belardo.A note on the signless Laplacian eigenvalues of graphs ［J］. Linear Algebra and its Applications，2011，435：2585-2590.

〔10〕P.Hansen，C.Lucas，Bounds and conjectures for the signless Laplacian indexof graphs［J］.Linear Algebra and itsApplications，2010，432：3319-3336.

〔11〕M.Lepovic，I.gutman.Some Spectral Properties of Stralike trees［J］.Bull.Acad.Serbe Sci.Arts，Cl.Sci.Math. Natur.，Sci.Math，2001，137（33）：99-105.

〔12〕M.Lepovic.Some results on Starlike trees and Sunlike graphs［J］.J.Appl.Math.&Computing，2003 11（1-2）：109-123.

〔13〕C.J.Bu，J.Zhou，Starlike treeswhose maximum degree exceed4 are determined by their Q-spectra［J］. Linear Algebra and itsAppli-cations，2012，436：143-151.

〔14〕S.N.Qiao.Thestarlike treeswith maximum and minimum secondorder connectivity index［J］.J Appl. Math Comput 2012（39）：523-532.

O157.5

A

1673-260X（2015）05-0004-02