創意平板折疊桌的設計及優化模型
劉雅倩,朱家明,曾淑嫻
(1.安徽財經大學 金融學院;2.安徽財經大學 統計與應用數學學院,安徽 蚌埠 233030)
創意平板折疊桌的設計及優化模型
劉雅倩1,朱家明2,曾淑嫻2
(1.安徽財經大學 金融學院;2.安徽財經大學 統計與應用數學學院,安徽 蚌埠 233030)
本文針對一款新型的創意平板折疊桌的設計加工問題,參考立體幾何學、物理力學、線性規劃等理論,分別構建了動態變化過程描述模型與最優加工參數規劃模型以及創意平板折疊桌設計模型,通過使用Matlab、Excel等軟件,求解了模型中所涉及的各種問題并給出了具體的結論.
創意折疊桌;受力分析;立體幾何;規劃模型;Matlab
某公司生產一種可折疊的桌子[1],桌面呈圓形,桌腿隨著鉸鏈的活動可以平攤成一張平板.桌腿由若干根木條組成,分成兩組,每組各用一根鋼筋將木條連接,鋼筋兩端分別固定在桌腿各組最外側的兩根木條上,并且沿木條有空槽以保證滑動的自由度.這款桌子設計復雜,需要綜合用料,加工,桌子本身穩定性各個方面的綜合考慮.本文試圖建立模型描述此折疊桌的動態變化過程,并討論長方形平板材料和折疊桌的最優設計加工參數(相關數據見2014年高教社杯全國大學生數學建模競賽賽題[2]).
1 折疊桌動態變化過程的數學描述
1.1 研究思路
在折疊桌展開過程中的任意時刻鋼筋總是貫穿所有木條,由于鋼筋是固定在最外面的那根木條上,首先計算出某一時刻t最外根木條的空間位置,再由最外根木條的位置計算鋼筋的位置,除四根著地的木條外,其他所有木條的位置只受到兩個約束條件:木條槽底端與鋼筋的接觸點和木條頂端與桌面的接觸點,根據這兩點可以分別求出其他木條的位置,通過畫出不同時刻的折疊桌打開瞬時圖來表現桌子的動態圖.這里設定長方形平板尺寸為120cm×50cm× 3cm,每根木條寬2.5cm,連接桌腿木條的鋼筋固定在桌腿最外側木條的中心位置,折疊后桌子的高度為53cm.
1.2 模型的建立
要得到曲面方程,首先要對相對靠近外側的兩條木條即木條1和木條2進行分析,推導出一般的規律方程.首先分析桌子的俯視圖,見圖1.

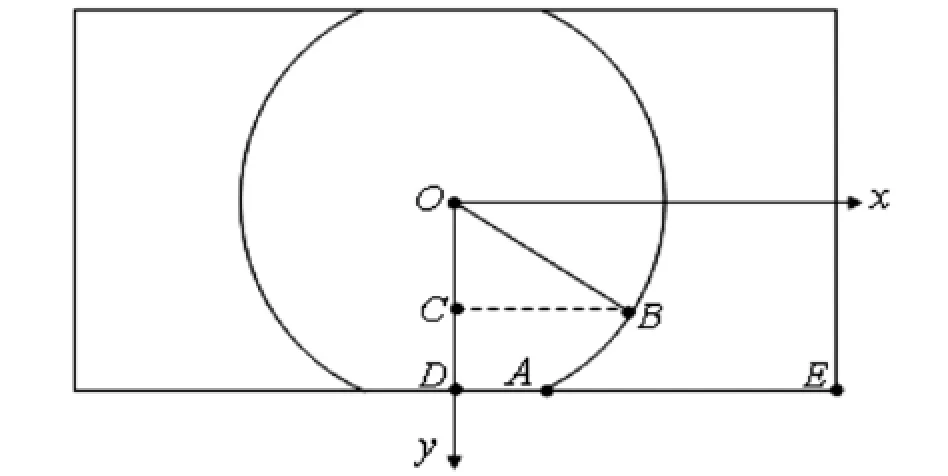
圖1 桌面俯視示意圖
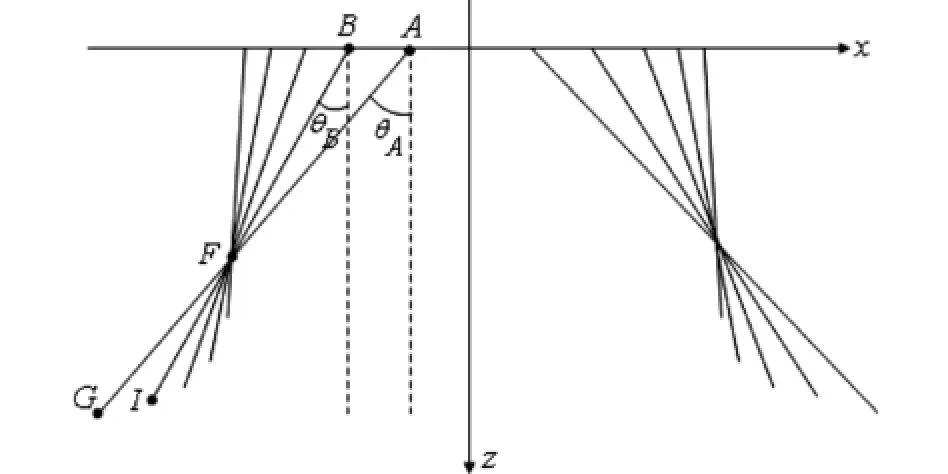
圖2 桌面最終狀態側面圖示意圖
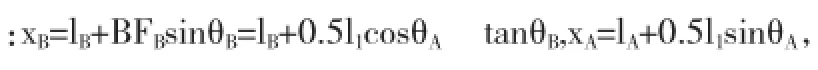

2 折疊桌最優設計加工參數的確定
2.1 研究思路
這里以折疊桌的設計穩固性好、用材最少為原則[3],建立多目標線性規劃,再對兩個目標分別賦予權重,將多目標線性規劃[4]進行分步規劃,使問題轉化為單目標線性規劃,求解出最優設計加工參數.這里假定桌高70cm,桌面直徑80cm.
2.2 研究準備
折疊桌的穩固性主要取決于兩個因素:折疊桌的重心位置和木條承受能力.

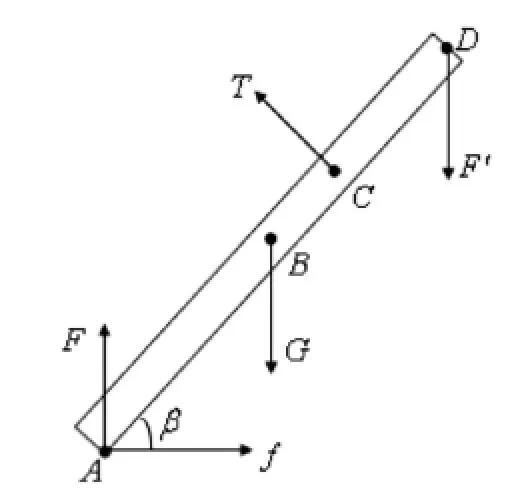
圖4 第一種受力分析示意圖

圖5 第二種受力分析示意圖
圖中B點為著地木條重心位置,A點為該根木條著地位置,C點為鋼筋與著地木條交點位置,F為地面給木條提供的支持力,f為地面給木條提供摩擦力,G為木條重力,T為鋼筋給木條提供拉力,設AC長度為x,容易知道θ+β=π/2.以第一種受力情況為例,對木條進行力矩分析:
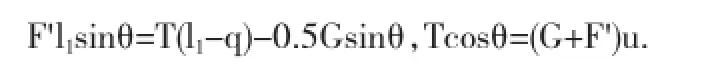
2.3 模型的建立
以第一種受力情況為例,建立如下方程組.方程組的約束條件是穩定性最大與用材最少,方程組的第一個式子反映了各個木條長度與各變量之間的關系,第二個式子是反應的是折疊桌處于最終狀態時相鄰兩木條與豎直方向夾角之間的推導關系,第三個式子衡量的是設計木桌的重心所在位置,第四個式子是根據受力分析以分析桌子的最大載重情況,第五個式子和第六個式子是鋼筋在木條上位置的約束條件.

2.4 模型的求解
鑒于多目標線性規劃求解較為復雜,采取分步規劃與控制變量相結合的方法來求解[5].
2.4.1 關于角度θ1的規劃
桌子處于最終狀態時,位于邊緣的著地木條與豎直方向的夾角θ1,而這個夾角對于桌子的穩定性,桌子的參數設計等因素產生重要的影響.所以先對角度的變化范圍進行規劃分析.畫出桌子最終打開狀態的簡單的俯視圖,如果穿過所有桌腿的鋼筋即圖中的AB與桌面也就是圓O相離,則桌子的穩定性會變差,所以鋼筋位置的臨界值是鋼筋AB與圓O相切的位置,見圖7.根據這一臨界位置算出θ1的臨界角度,計算原理見圖8.

圖7 鋼筋位置臨界情況示意圖
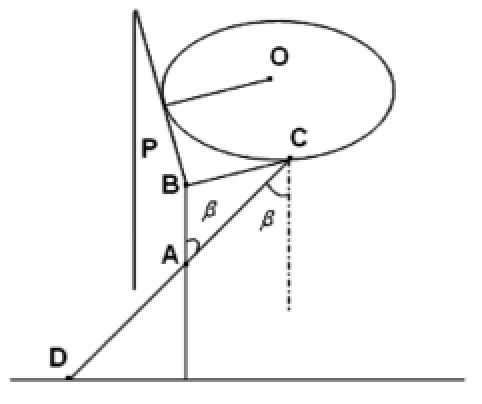
圖8 θ1的臨界角度的計算原理圖
圖8中鋼筋所在的與桌面相切的平面為面P,AD為折疊桌最外根木條的鋼筋位置距木條地面的距離q,DC為折疊桌最外根木條的長度l1,CB等于桌面半徑e/2.CD與豎直方向夾角為β.當鋼筋位置在面P外時,折疊桌無法維持穩定,所以圖示β為木條夾角的最大值,根據正弦定力可知sinβ=BC/AC=BC/(CD-AD)=e/2(l1-q),由此可求出β,得到木條夾角取值的最大值為46°.研究一計算θ1值為22.8°,并且分析角度不可能過小,這里確定的θ1的變化范圍是12° 到46°,同時設定θ1變動的步長值為2°.將桌高70cm,桌面直徑80cm,u=0.5帶入轉化后目標函數,得到簡化模型.將結果做成圖形以直觀地看出變動趨勢,見圖4.

根據上述方程式,計算出不同的夾角對應的折疊桌的承受力,并作出如下圖形.
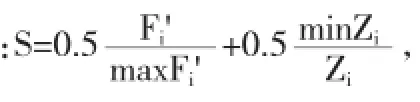
2.4.2 整體的規劃結果
綜上所述:對于任意給定的折疊桌高度和圓形桌面直徑,折疊桌的最優設計加工參數為:平板的長為189cm;鋼筋所在位置到折疊桌最外根木條底端的距離為19.52cm,即位于折疊桌最外根木條的1/3處;開槽長度結果見下表.

圖9 不同θ1的取值對折疊桌承受力的影響示意圖

表1 開槽長度結果值

3 總結
通過確定的鋼筋位置和桌面寬度建立模型,接著根據算出的桌腿長度,根據立體幾何學知識,給出桌子的動態變化描述模型;要想給出桌子的最優設計參數,首先通過對折疊桌的受力與重心位置的分析建立折疊桌的穩固性約束方程,結合研究一的結論,進一步考慮加工的方便性和用材的效益性,從而建立一個多目標規劃模型.通過利用分步規劃、控制變量法與曲線擬合等方法,計算出在給定桌高與桌面直徑的數值,計算出的最優解為:木條根數為32根,木板長度為 189.148cm,鋼筋在木條上的位置離木條末端為19.517cm.
〔1〕平板邊桌:Rising Side Table[EB/OL],http://www.ixiqi. com/archives/47763.2014-09-12/2012-07-09.
〔2〕2014年高教社杯全國大學生數學建模競賽賽題[EB/ OL],http://www.mcm.edu.cn/html_cn/node/ 93b5f5d9986693c2ebd67962cdc7d9df.html.2014-09-15/ 2014-09-12.
〔3〕向高軍,季廷洪,杜博亞.創意平板折疊桌的設計[J].硅谷,2015(01).
〔4〕邱松強.非線性規劃的可行性控制方法及其應用[D].蘇州大學,2013.
〔5〕李朝霞.線性規劃的數學模型及實際應用[J].宿州教育學院學報,2006(01).
TS665.3
A
1673-260X(2015)05-0040-03
國家自然科學基金項目資助(11301001);安徽財經大學教研項目資助(acjyzd201429)

